Matlab通信仿真系列——信号处理函数_matlab信号处理常用函数

微信公众号上线，搜索公众号小灰灰的FPGA,关注可获取相关源码，定期更新有关FPGA的项目以及开源项目源码，包括但不限于各类检测芯片驱动、低速接口驱动、高速接口驱动、数据信号处理、图像处理以及AXI总线等

本节目录

一、Matlab信号产生函数
(1)随机信号函数
(2)方波信号函数
(3)锯齿波信号函数
(4)正弦波信号函数
二、Matlab信号分析函数
(1)滤波函数filter
(2)单位抽样响应函数impz
(3)频率响应函数
(4)零极点增益函数
(5)快速傅里叶变换函数
三、Matlab源码
(1)Matlab信号产生函数源码
(2)Matlab信号分析函数源码一
(3)Matlab信号分析函数源码二
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

本节内容
一、Matlab信号产生函数
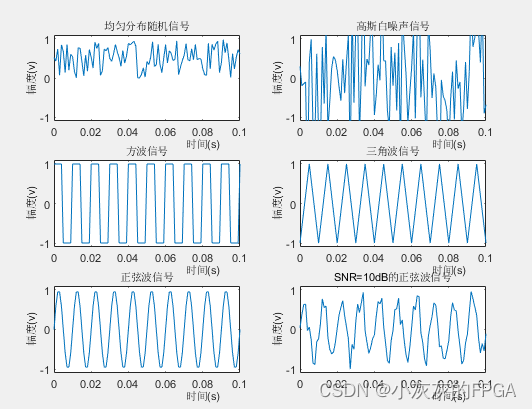
在进行数字信号处理仿真或设计时，需要产生随机信号、方波信号、锯齿波信号、正弦信号，以及带有加性白噪声的某种输入信号。
(1)随机信号函数
Matlab提供了两种随机信号产生函数rand(1,N)和randn(1,N)
rand——产生长度为N的在[0,1]上均匀分布的随机序列
randn——产生均值为0,方差为1的高斯随机序列，功率为1W的白噪声序列
具有其他分布特性的序列可以由这两种随机数变换产生。
(2)方波信号函数
Matlab提供了方波信号产生函数square。
两种格式square(T)和square(T,DUTY)
square(T)——对时间变量T产生周期为2π，幅值为±1的方波
square(T,DUTY)——产生指定占空比的方波，DUTY指定信号为正值的区域在一个周期T内所占的比例，取值为0-100，当DUTY为50时，产生方波信号，与square(T)函数相同
(3)锯齿波信号函数
Matlab提供的锯齿波函数sawtooth。
有两种格式sawtooth(T)和sawtooth(T，WIDTH)
sawtooth(T)——对时间变量T产生周期为2π，幅值为±1的锯齿波
sawtooth(T，WIDTH)——对时间变量T产生三角波，WIDTH指定三角波的尺度值，取值为0-1，当WIDTH为0.5时，产生对称的三角波信号，当WIDTH为1时，产生锯齿波信号。
(4)正弦波信号函数
Matlab提供了完整的三角函数，如正弦函数sin、双曲正弦函数sinh、反正弦函数asin、反双曲正弦函数asinh、余弦函数cos、双曲余弦函数cosh、反余弦函数acos、反双曲余弦函数acosh、正切函数tan、余切函数cot等。均是对时间变量T产生周期为2π,幅值为±1的对应函数。

二、Matlab信号分析函数
(1)滤波函数filter
filter是利用递归滤波器或非递归滤波器对数据进行滤波处理的函数。
任何一个离散系统可以作为一个滤波器，系统的输出即输入信号经过滤波器滤波后的结果。
一个N阶的离散系统函数

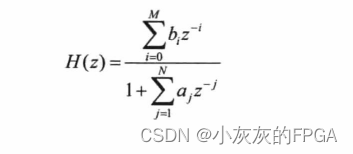
差分方程为

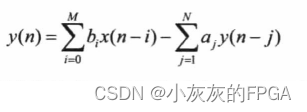
filter函数有三个参数：filter(b,a,x)
b为系统函数的分子项组成的行矩阵
a为系统函数的分母项组成的行矩阵
x为输入信号序列
函数返回值为输入序列x经滤波处理后的输出结果
(2)单位抽样响应函数impz
Matlab提供了一个可以直接求取系统单位抽样响应的函数impz
impz函数有两种用法：impz(b,a,p)及h=impz(b,a,p)
b、a为系统函数向量
p为计算的数据点数
h为单位抽样响应结果数据
impz(b,a,p)是直接在Matlab中绘制系统的单位响应杆图(Stem)
h=impz(b,a,p)是将单位抽样响应结果存入变量h中，但不绘图
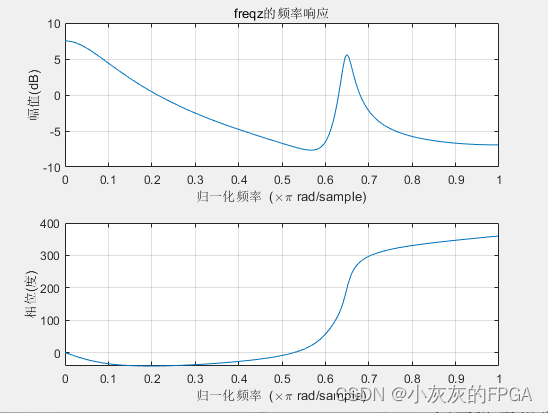
(3)频率响应函数
频率响应指系统的幅频(幅度-频率)响应及相频(相位-频率)响应。
频率响应是系统最基本最重要的特征，在设计系统时，通常以达到系统所需要的频率响应为目标。
Matlab提供了获取系统的频率响应的函数freqz
freqz有两种用法：freqz(b,a,n,Fs)及[h,f]=freqz(b,a,n,Fs)
b、a分别为系统函数向量
Fs为采样频率
n为在[0,Fs/2]范围内计算的频率点数量，并将频率值存放在f中
h存放频率响应计算结果
freqz(b,a,n,Fs)可直接绘出系统的幅频响应及相频响应曲线
[h,f]=freqz(b,a,n,Fs)将频率响应结果存放在h及f变量中，但不绘图
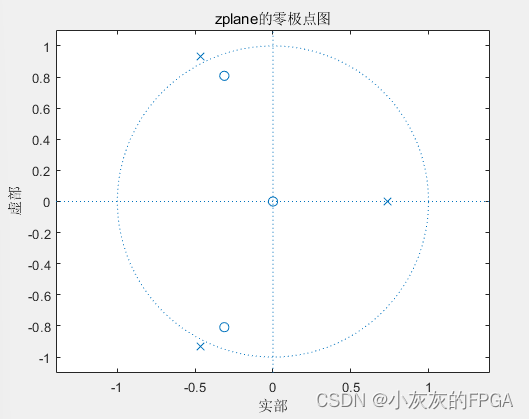
(4)零极点增益函数
对于离散系统，系统的零极点及增益参数可明确地反映系统的因果性、稳定性等重要特性，进行系统分析及设计时需计算其零极点和增益参数。
Matlab提供root函数来计算系统的零极点，直接使用zplane函数画出系统的零极点图。




(5)快速傅里叶变换函数
快速傅里叶变换(Fast Fourier Transform,FFT)，充分利用离散傅里叶变换(Discrete Fourier Transform,DFT)运算中的对称性和周期性，从而将DFT运算量N^2(N为计算的数据点数)减少到Nlog2(N)。
N较小时，FFT优势并不明显，但当N大于32时，点数越大，FFT对运算量的改善越明显。
Matlab提供了fft及ifft两个函数分别用于快速傅里叶正/反变换。
常用方法y=fft(x,n)
x是输入信号序列
n是参与计算的数据点数，通常取2的整数幂次方
y存放函数运算结果
当n大于输入序列的长度，fft函数在x的尾部补零构成n点数据
当n小于输入序列的长度，fft函数对序列x进行截尾。

三、Matlab源码
(1)Matlab信号产生函数源码

%产生方波、三角波及正弦波序列信号
%定义参数
Ps=10;          %正弦信号功率为10dB
Pn=1;           %噪声信号功率为0dB
f=100;          %信号频率为100Hz
Fs=1000;        %采样频率为1kHz
width=0.5;      %函数sawtooth()的尺度参数为0.5
duty=50;        %函数square()的尺度参数为50
%产生信号
t=0:1/Fs:0.1;
c=2*pi*f*t;
sq=square(c,duty);      %产生方波
tr=sawtooth(c,width);   %产生三角波
si=sin(c);              %产生正弦波
%产生随机信号
noi=rand(1,length(t));      %产生均匀分布的随机序列
noise=randn(1,length(t));   %产生高斯白噪声序列
%产生带有加性高斯白噪声的正弦信号序列
sin_noise=sqrt(2*Ps)*si+sqrt(Pn)*noise;
%归一化处理
sin_noise=sin_noise/max(abs(sin_noise));
%绘图
subplot(3,2,1);
plot(t,noi);
axis([0 0.1 -1.1 1.1]);
xlabel('时间(s)','fontsize',8,'position',[0.08,-1.5,0]);
ylabel('幅度(v)','fontsize',8);
title('均匀分布随机信号','fontsize',8);

subplot(3,2,2);
plot(t,noise);
axis([0 0.1 -1.1 1.1]);
xlabel('时间(s)','fontsize',8,'position',[0.08,-1.5,0]);
ylabel('幅度(v)','fontsize',8);
title('高斯白噪声信号','fontsize',8);

subplot(3,2,3);
plot(t,sq);
axis([0 0.1 -1.1 1.1]);
xlabel('时间(s)','fontsize',8,'position',[0.08,-1.5,0]);
ylabel('幅度(v)','fontsize',8);
title('方波信号','fontsize',8);

subplot(3,2,4);
plot(t,tr);
axis([0 0.1 -1.1 1.1]);
xlabel('时间(s)','fontsize',8,'position',[0.08,-1.5,0]);
ylabel('幅度(v)','fontsize',8);
title('三角波信号','fontsize',8);

subplot(3,2,5);
plot(t,si);
axis([0 0.1 -1.1 1.1]);
xlabel('时间(s)','fontsize',8,'position',[0.08,-1.5,0]);
ylabel('幅度(v)','fontsize',8);
title('正弦波信号','fontsize',8);

subplot(3,2,6);
plot(t,sin_noise);
axis([0 0.1 -1.1 1.1]);
xlabel('时间(s)','fontsize',8,'position',[0.08,-1.5,0]);
ylabel('幅度(v)','fontsize',8);
title('SNR=10dB的正弦波信号','fontsize',8);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

(2)Matlab信号分析函数源码一

L=128;                          %单位抽样序列的长度
Fs=1000;                        %采样频率为1kHz
b=[0.8 0.5 0.6];                %系统函数的分子系数向量
a=[1 0.2 0.4 -0.8];             %系统函数的分母系数向量
delta=[1 zeros(1,L-1)];         %生成长度为L的单位抽样序列

Filter_out=filter(b,a,delta);   %filter函数获取单位抽样响应
Impz_out=impz(b,a,L);           %impz函数获取单位抽样响应
[h,f]=freqz(b,a,L,Fs);          %freqz函数求频率响应
mag=20*log10(abs(h));           %幅度转换dB单位
ph=angle(h)*180/pi;             %相位值单位转换
zr=roots(b);                    %求系统的零点
pk=roots(a);                    %求系统的极点
g=b(1)/a(1);                    %求系统的增益

%绘图
figure(1);
subplot(2,2,1);
stem(Filter_out);
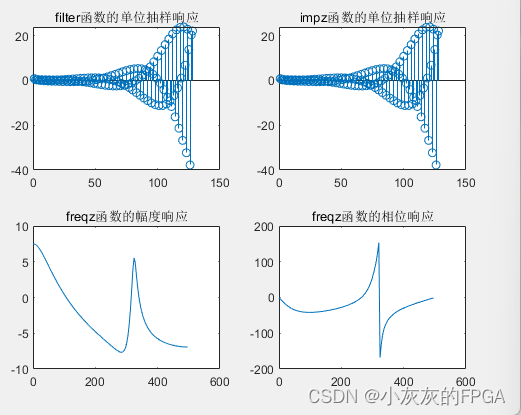
title('filter函数的单位抽样响应');
subplot(2,2,2);
stem(Impz_out);
title('impz函数的单位抽样响应');
subplot(2,2,3);
plot(f,mag);
title('freqz函数的幅度响应');
subplot(2,2,4);
plot(f,ph);
title('freqz函数的相位响应');
%用freqz绘制频率响应
figure(2);
freqz(b,a);
title('freqz的频率响应');
%用zplane绘制零极点图
figure(3);
zplane(b,a);
title('zplane的零极点图');
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

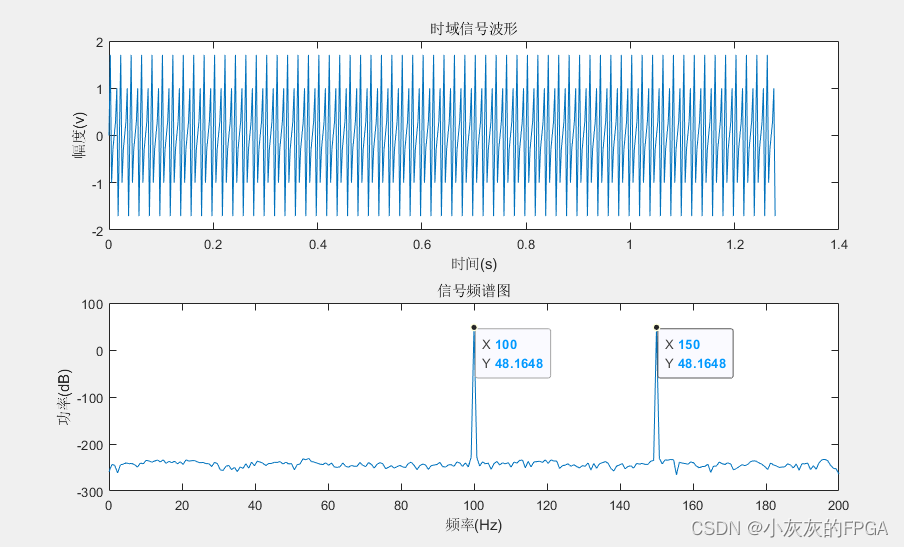
(3)Matlab信号分析函数源码二

N=512;      %数据长度
f1=100;     %f1信号频率，单位Hz
f2=150;     %f2信号频率，单位Hz
Fs=400;    %采样评论，单位Hz

t=0:1/Fs:1/Fs*(N-1);                %产生时间序列
s=sin(2*pi*f1*t)+sin(2*pi*f2*t);    %产生两个频率信号的叠加信号
f=fft(s,N);                         %计算傅里叶变换
f=20*log10(abs(f));                 %转化成dB单位
ft=[0:(Fs/N):Fs/2];                 %转化横坐标以Hz为单位
f=f(1:length(ft));                  

%绘图
subplot(2,1,1);
plot(t,s);
xlabel('时间(s)');
ylabel('幅度(v)');
title('时域信号波形');

subplot(2,1,2);
plot(ft,f);
xlabel('频率(Hz)');
ylabel('功率(dB)');
title('信号频谱图');
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24