Matlab|【免费】面向多微网网络结构规划的大规模二进制矩阵优化算法

目录

1 主要内容

节点故障网络拓扑变化示意

约束条件

目标函数

3 结果一览

4 下载链接

---

1 主要内容

当前电力系统中微电网逐步成为发展的主力军，微网中包括分布式电源和负荷，单一的微电网是和外部电源进行连接，即保证用电的效益性，也要保证系统的稳定性，但是多个微电网是否可考虑通过电力网络结构设计来增加系统的鲁棒性，正是本模型考虑的内容。在该研究中，将多微网结构设计问题转化为数据模型，根据系统特点考虑了三种不同的节点类型，并通过基于大规模二进制矩阵的差分进化算法进行优化求解，通过算例验证了方法的有效性。该程序采用matlab编写，模块化编程，有部分注释，有需要的同学可以下载研究。

• 节点故障网络拓扑变化示意

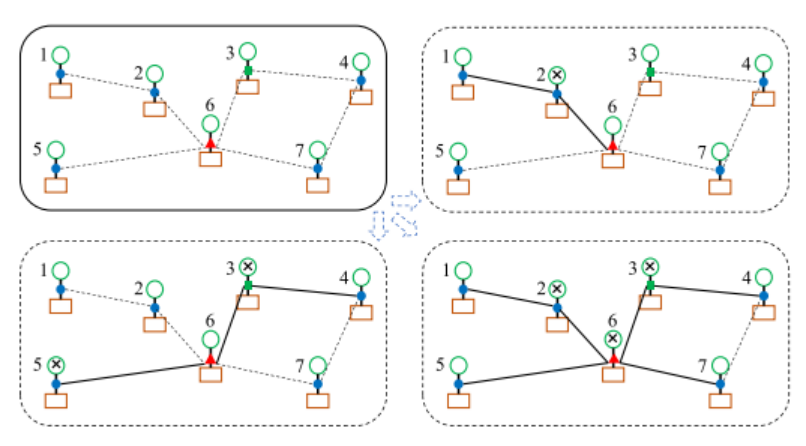
不同节点故障后，故障节点需要其他节点电源帮助恢复供电，上图即为三种情况下网络拓扑变化示意图。

• 约束条件

对于I型节点来说，在节点i电源故障时，该类节点需要通过相邻节点电源进行补偿，以维持I节点负荷正常运转，也就是系统需要满足N-1的要求。该类节点约束的数学模型如下：

Si代表相邻节点对i节点可提供的电源功率支撑能力，Gj和Lj分别代表j节点的电源和负荷，通过上面约束能够看出，相邻节点的功率需要完全支撑起i节点的负荷。

对于II型节点，需满足两个节点同时故障仍然能保证系统正常工作，对应的约束数学模型如下：

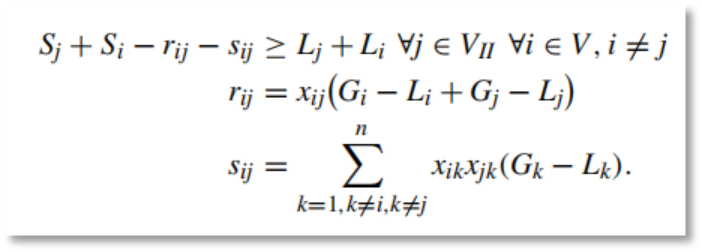
对于III型节点，​需要满足系统N-3的要求，对应约束的数学模型如下：

• 目标函数

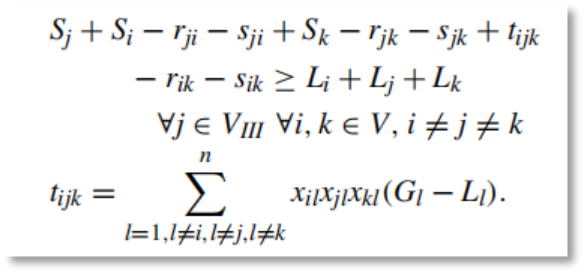
该模型的主要任务是需要系统满足N-k的需求，并确保系统具有稳定性和鲁棒性，从成本角度来看，其目标是需要微网间连接线总长度最小，具体数学模型如下：

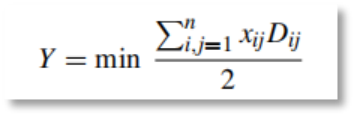
2部分代码

clear; clc; close all
addpath(genpath(pwd));
​
nP = 20; % Number of nodes, options: 10, 20, 50, 80, 100
pID = 1; % Dataset ID, range: 1-5
timer = tic;
%% Problem parameter settings
load(['MNSDP-LIB\MNSDP_' num2str(nP) '_' num2str(pID) '.mat']);
​
%% Parameter settings
PopSize = min(10*MCS.N,500); % Population size
MaxGen = 50*MCS.N; % Maximum number of generations
plt = 1; % Whether to draw real-time optimization graphs during execution, default is off (can greatly improve running speed)
​
%% Initialization
Population = Init(PopSize,pID,MCS);
ConvergenceF = zeros(2,PopSize);
ConvergenceCV = zeros(2,PopSize);
Gb=inf;
​
%% Start optimization and solving
fprintf('Number of nodes: %3d, Dataset ID: %d\n', nP, pID)
BMODE();
​
%% Optimization completed
timer = toc(timer);
disp(['Time used: ' num2str(timer) ' seconds']);
BestSol = BestInd(end);
​
figure
PlotSol() % Plot solution
​

3 结果一览

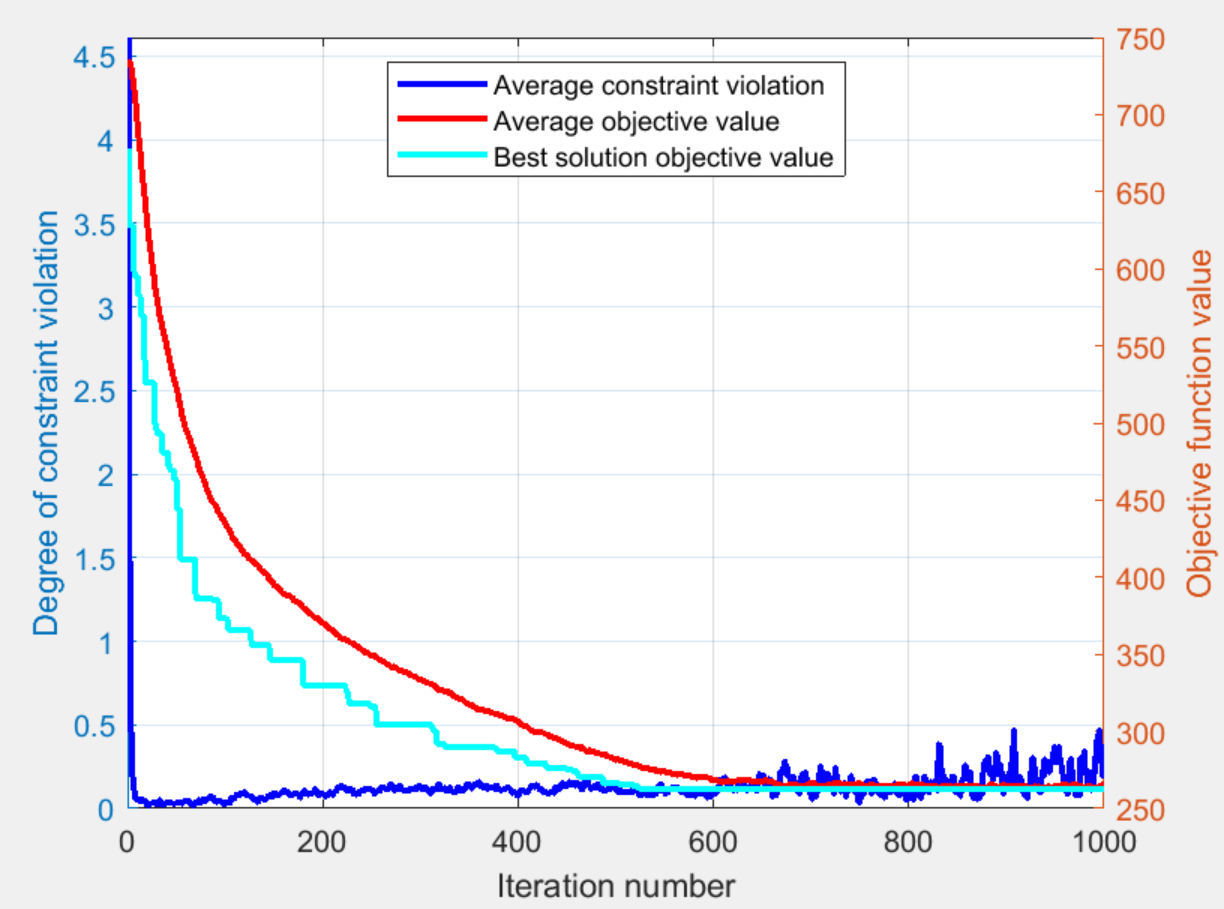
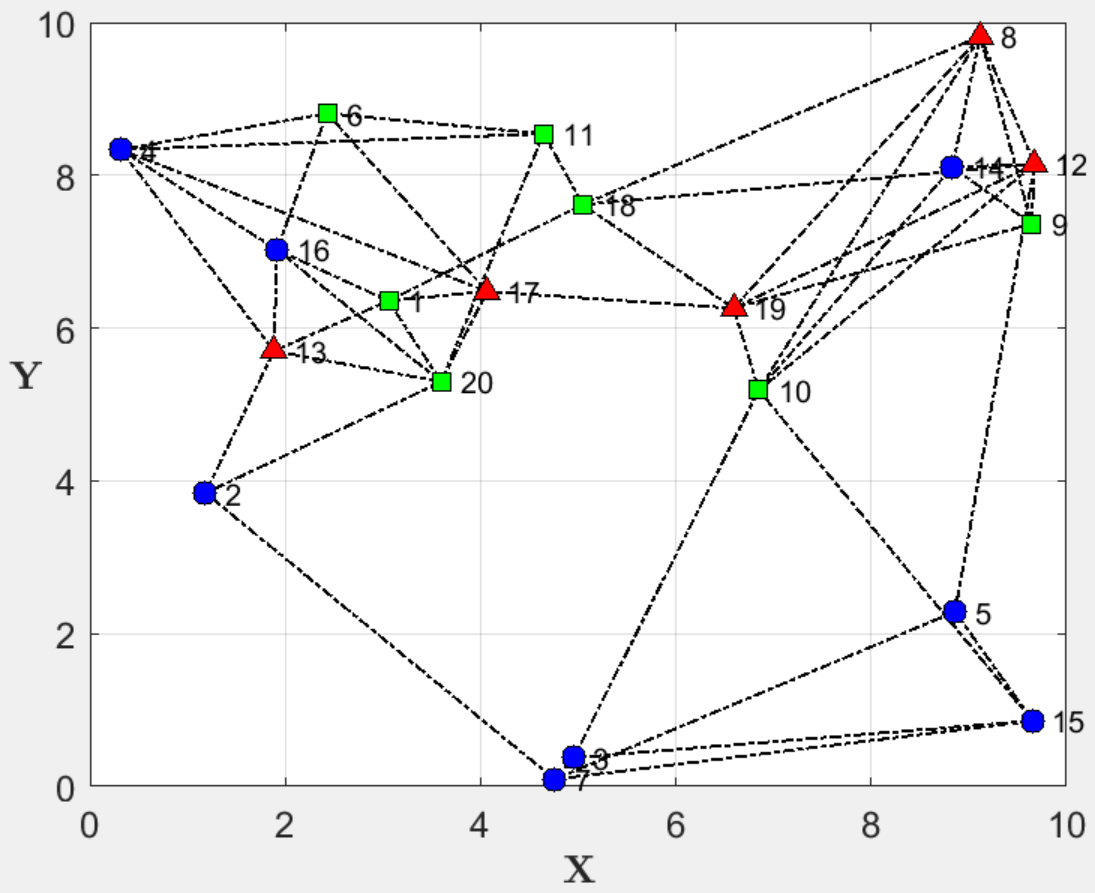
4 下载链接

​