数据结构--图。

在前面，我们学习了线性表和树，而接下来我们要学习的图相较于他们就更加复杂。

目录

一.图的有关概念

---

一.图的有关概念

1.定义

图(graph)G由两个集合V和E组成，记为G=（VE)。V是顶点的有穷非空集合;E是边的集合,边是V中顶点的无序对或有序对。E可以是边的空集，者E为空集，则G中只有顶点没有边。

2.由于“弧”是有方向的，因此称由顶点集和弧集构成的图为有向图。

3.顶点:在图中的数据元素

4.弧:若<v，w> VR，则<v，w>表示从v到w的一条弧

 弧尾：v(起始点)

 弧头：w(终端点)

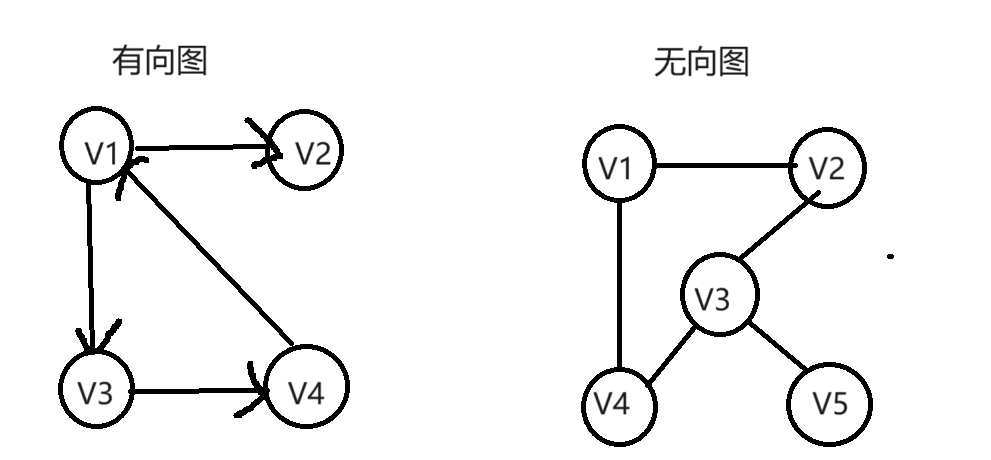
5.有向图：是图论中的一种重要概念，用于描述各种事物之间的有序关系。它由一组节点（或顶点）以及连接这些节点的有向边组成。每条边都有一个方向，从一个节点指向另一个节点，表示了它们之间的关系和方向性

  无向图：边没有方向的图

6.完全图：有n(n-1)/2条边的无向图

  有向完全图：对于有向图，e的取值范围是0到n(n-1)，具有n(n-1)条弧的有向图

  无向完全图：n个顶点的无向图，每个顶点与其他n-1个顶点都有边，具有最大边数n（n-1）/2

7.稀疏图：有很少条边或弧的图

  稠密图：图的边或弧很多

8.权：与图的边或弧相关的数

  网：带权的图

9.邻接点：假若顶点v和顶点w之间存在一条边，那么v和w互为邻接点

10.度：无向图中，与其相关联的边的数目

  入度：(有向图)以顶点v为头的弧的数目

  出度：(有向图)以顶点v为尾的弧的数目

11.路径长度：沿路径边的数目或沿路径各边权值之和

    回路：第一个顶点和最后一个顶顶点相同的路径

    简单路径：序列中顶点不重复出现的路径

    简单回路:除了第一个顶点和最后一个顶点外，其余顶点不重复出现的回路

12.连通：无向图中如果从顶点V到顶点W有一条路径，则说V和W是连通的

  连通图：无向图中任意两个顶点都是连通的

  连通分量：无向图中的极大连通子图

  强连通分量：有向图中的极大强连通子图

13.生成树：一个极小连通子图，它含有图中全部顶点，但只有足以构成一棵树的n一1条边

二.图的存储结构

2.1.图的数组(邻接矩阵)存储表示

2.1.1图的邻接矩阵表示法的特点

·对于无图：

 邻接矩阵一定是一个对称矩阵

 行（列）非零元素个数，表示度

·对于有向图:

 矩阵不一定是一个对称矩阵

行非零元素个数，表示出度

·列非零元素个数，表示入度

2.1.2应用

通过邻接矩阵判定任意两个顶点之间是否有边相连

2.邻接表

是图的一种链式存储结构

特点

无向图中顶点VI的度为第1个单链表中的结点

有向图中

顶点Vi的出度为第1个单链表中的结点个

顶点Vi的入度为整个单链表中邻接点城#

值是的结点个数

逆邻接表:有向图中对每个结点建立以Vi为头

的弧的单链表

3.十字链表

4.邻接多重表

三.图的遍历

3.1.深度优先搜索

3.1.1连通图

3.1.2非连通图

3.2.广度优先搜索

四.应用

4.1.图的连通性问题

4.1.1无向图的连通分量和生成树

4.1.2有向图的强连通分量

4.1.3最小生成树

4.1.4关节点和重连通分量

4.2有向无环图

4.3拓扑排序

4.4关键路径

4.5最短路径