【算法】二分查找——在排序数组中查找元素的第一个和最后一个位置

本节博客主要是通过“在排序数组中查找元素的第一个和最后一个位置”总结关于二分算法的左右界代码模板，有需要借鉴即可。

1.题目

题目链接：LINK

这个题要求我们求这个排序数组的一个元素的开始位置与结束位置。

可以用暴力求解的方法，把第一次出现的数字下标记录一下，最后一次记录一下，返回结果，除了复杂度差之外没什么不好的。

当然我们这里说一下二分算法的思想。之所以可以使用二分算法，这是因为该数组是有序的，可以利用二分算法的“二段性”将其分割。

用两次二分算法：

• 一方面，我们可以将整个数组分为大于等于t和小于t来找left点

• 另一方面，我们可以将整个数组分为大于t和小于等于t来找right点

但是这里有一些代码细节值得注意！！！

2.二分边界算法

2.1查找区间左端点

思考：我们在寻找左端点时候为什么要对数组按照小于t和大于等于t进行划分？
答：关键是因为我们要找左端点，左端点一定不可能在小于t的区间里。

通过上面的图片可知，我们要想找到一个数的左端点，那么这个左端点(我们要寻找的点)一定不再大于t这个区域，所以我们可知

• mid < ret时，left = mid + 1
• mid >= ret时，right = mid

2.1.1循环条件

while(left < right)//... √
while(left <= right)//... ×
1
2

循环条件选：left < right

这里为什么不是left <= right 呢？

• left==right的情况下，即是最后结果，无需进行重复判断。
• 可能有些情况下会出现死循环问题
  下面是对上面两个理由进行论证：
  在所有可能情况中，无非存在三种情况，
• ①left与right中间存在要找的ret点
  
  此时，mid = ret,mid == right,那么left = mid，会不断进入循环，陷入死循环。
• ②left与right中间所有点全部大于我们要找的右端点
  
  到了最后，mid > ret, mid = right，right = mid，会存在死循环问题
• ③left与right中间所有点全部小于我们要找的右端点
  
  mid < ret,left = mid + 1,不会出现死循环问题。

2.1.2求中点的操作

我们求中点无非两种求法

①mid = left + (right - left) / 2; √
②mid = left + (right - left + 1) / 2; ×
1
2

这俩主要区别就是在数字个数是偶数情况下，①式取靠左的中点；②式取靠右的中点。

然后对于查找区间右端点而言，必须选用①式。
为什么，下面来进行解释？
如果选用②式，会存在下面情况：比如，mid指向right，然后mid所在的值>=ret值，就会不断死循环
注：if mid >= ret,right = mid;

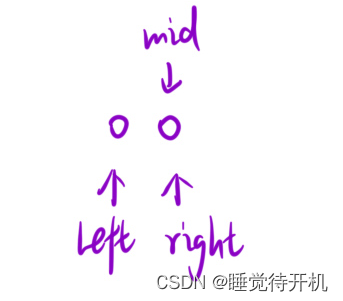
2.1.3总结

在求目标值左端点时候，第一循环条件不能有等于，第二是求中点要用靠右中点。

2.2查找区间右端点

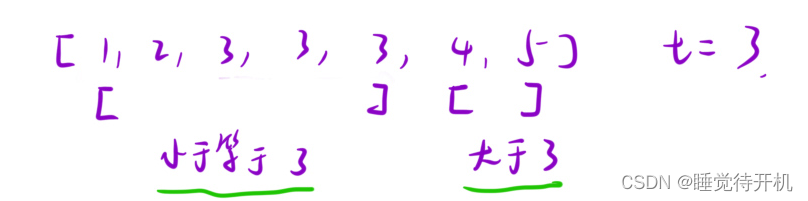
通过上面的图片可知，我们要想找到一个数的左端点，那么这个右端点(我们要寻找的点)一定不再大于t这个区域，所以我们可知

• mid <= ret时，left = mid
• mid > ret时，right = mid - 1

2.1.1循环条件

while(left < right)//... ×
while(left <= right)//... √
1
2

循环条件选：left < right

这里为什么不是left <= right 呢？

• left==right的情况下，即是最后结果，无需进行重复判断。
• 可能有些情况下会出现死循环问题

下面是对上面两个理由进行论证：
在所有可能情况中，无非存在三种情况，

• ①left与right中间存在要找的ret点
  
  此时，mid = ret,mid == right,那么right = mid，会不断进入循环，陷入死循环。
• ②left与right中间所有点全部大于我们要找的右端点
  
  到了最后，mid > ret,mid == right，right = mid - 1，不会出现死循环问题
• ③left与right中间所有点全部小于我们要找的右端点
  
  mid < ret,left = mid,此时会出现死循环问题。

2.1.2求中点的操作

我们求中点无非两种求法

①mid = left + (right - left) / 2; ×
②mid = left + (right - left + 1) / 2; √
1
2

这俩主要区别就是在数字个数是偶数情况下，①式取靠左的中点；②式取靠右的中点。

然后对于查找区间右端点而言，必须选用②式。
为什么，下面来进行解释？
如果选用①式，会存在下面情况：比如，mid指向left，然后mid所在的值<=ret值，left = mid,如此就会不断死循环
注：if mid <= ret,left = mid;

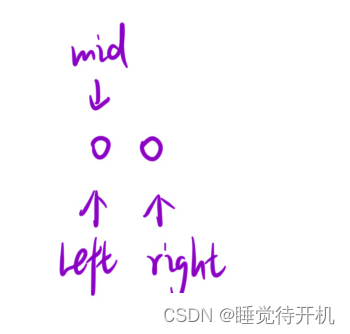
2.1.3总结

在求目标值右端点时候，第一循环条件不能有等于，第二是求中点要用靠右中点。

2.3总结

找左端点：

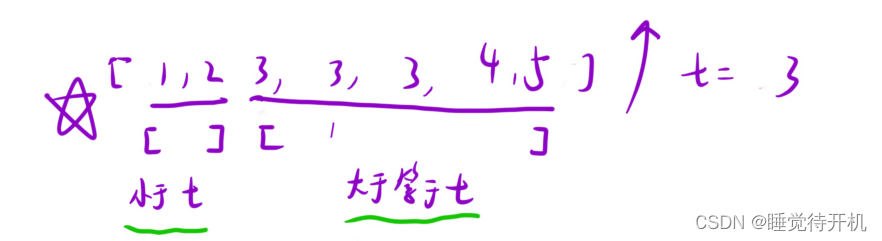
• mid < ret时，left = mid + 1
• mid >= ret时，right = mid

while(left < right)//...
mid = left + (right - left) / 2;
1
2

找右端点：

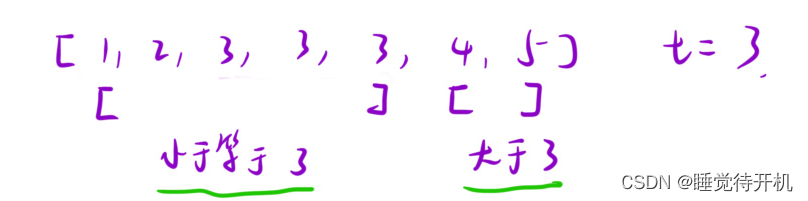
• mid <= ret时，left = mid
• mid > ret时，right = mid - 1

while(left < right)//...
mid = left + (right - left + 1) / 2;
1
2

根据上面的算法总结我们可以解决上面题目

3.参考解题代码

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) 
    {
        vector<int> ret;
        //处理特殊情况
        if(nums.size() == 0)
        {
            ret.push_back(-1);
            ret.push_back(-1);

            return ret;
        }

        int left = 0, right = nums.size() - 1;
        //处理左端点
        while(left < right)
        {
            int mid = left + (right - left) / 2;
            if(nums[mid] >= target)
            {
                right = mid;
            }
            else
            {
                left = mid + 1;
            }
        }
        if(nums[left] == nums[right] && nums[left] == target)
        {
            ret.push_back(left);
        }
        else
        {
            ret.push_back(-1);
        }

        //处理右端点
        left = 0, right = nums.size() - 1;
        while(left < right)
        {
            int mid = left + (right - left + 1) / 2;
            if(nums[mid] > target)
            {
                right = mid - 1;
            }
            else
            {
                left = mid;
            }
        }
        if(nums[left] == nums[right] && nums[right] == target)
        {
            ret.push_back(right);
        }
        else
        {
            ret.push_back(-1);
        }


        return ret;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64

4.模板总结

5.总结

这个题目我感觉掌握了二分边界代码原理其实不难，重点肯定是那个二分边界算法原理，需要自己多理解一下。

---

EOF