rpnnp的matlab,数学建模及机器学习算法（一）：聚类-kmeans（Python及MATLAB实现，包括k值选取与聚类效果评估）...

一、聚类的概念

聚类分析是在数据中发现数据对象之间的关系，将数据进行分组，组内的相似性越大，组间的差别越大，则聚类效果越好。我们事先并不知道数据的正确结果(类标)，通过聚类算法来发现和挖掘数据本身的结构信息，对数据进行分簇(分类)。聚类算法的目标是，簇内相似度高，簇间相似度低

二、基本的聚类分析算法

1. K均值(K-Means)：

基于原型的、划分的距离技术，它试图发现用户指定个数(K)的簇。

2. 凝聚的层次距离：

思想是开始时，每个点都作为一个单点簇，然后，重复的合并两个最靠近的簇，直到尝试单个、包含所有点的簇。

3. DBSCAN:

一种基于密度的划分距离的算法，簇的个数有算法自动的确定，低密度中的点被视为噪声而忽略，因此其不产生完全聚类。

三、距离量度

不同的距离量度会对距离的结果产生影响，常见的距离量度如下所示：

四、K-Means

在聚类算法中K-Means算法是一种最流行的、使用最广泛的一种聚类算法，因为它的易于实现且计算效率也高。聚类算法的应用领域也是非常广泛的，包括不同类型的文档分类、音乐、电影、基于用户购买行为的分类、基于用户兴趣爱好来构建推荐系统等。

优点：易于实现

缺点：可能收敛于局部最小值，在大规模数据收敛慢

算法思想：

1 选择K个点作为初始质心2 repeat3 将每个点指派到最近的质心，形成K个簇4 重新计算每个簇的质心5 until 簇不发生变化或达到最大迭代次数

这里的重新计算每个簇的质心，更新过程是：首先找到与每个点距离最近的中心点，构成每个中心点划分的k个点集，然后对于每个点集，计算点的均值代替中心点。

如何计算是根据目标函数得来的，因此在开始时我们要考虑距离度量和目标函数。

考虑欧几里得距离的数据，使用误差平方和(Sum of the Squared Error,SSE)作为聚类的目标函数，两次运行K均值产生的两个不同的簇集，我们更喜欢SSE最小的那个：

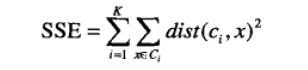
k表示k个聚类中心，ci表示第几个中心，dist表示的是欧几里得距离。

前面说的我们更新质心是让所有的点的平均值，这里就是SSE所决定的：

因此K-Means算法的实现步骤，主要分为四个步骤：

1、从样本集合中随机抽取k个样本点作为初始簇的中心。

2、将每个样本点划分到距离它最近的中心点所代表的簇中。

3、用各个簇中所有样本点的中心点代表簇的中心点。

4、重复2和3，直到簇的中心点不变或达到设定的迭代次数或达到设定的容错范围。

五、k-means代码实现

本文采用sklearn来实现一个k-means算法的应用，细节的底层实现可见文末第一个链接。

1.首先使用sklearn的数据集，数据集中包含150个随机生成的点，样本点分为三个不同的簇：

1 from sklearn.datasets importmake_blobs2 importmatplotlib.pyplot as plt3

4

5 if __name__ == "__main__":6 '''

7 n_samples：代表样本点的个数8 n_features：表示每个样本由两个特征组成9 center：表示样本点中心的个数(簇)10 cluster_std：表示每个样本簇方差的大小11 '''

12 x,y = make_blobs(n_samples=150,n_features=2,centers=3,13 cluster_std=0.5,shuffle=True,random_state=0)14 #绘点

15 plt.scatter(x[:,0],x[:,1],marker="o",color="blue")16 #以表格的形式显示

17 plt.grid()18 plt.show()

效果如下：

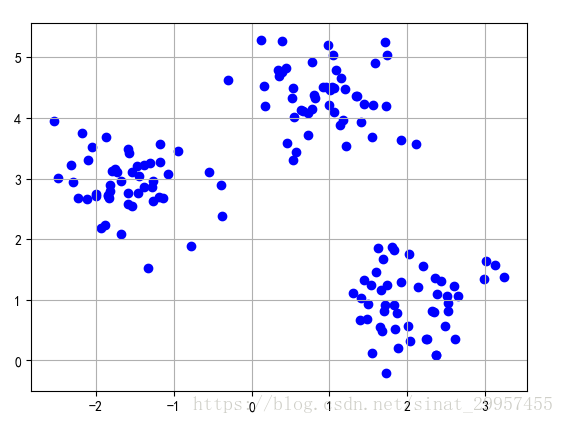
2.下面使用sklearn内置的KMeans算法来实现对上面样本点的聚类分析：

1 from sklearn.cluster importKMeans2 '''

3 n_clusters:设置簇的个数4 init:random表示使用Kmeans算法，默认是k-means++5 n_init:设置初始样本中心的个数6 max_iter:设置最大迭代次数7 tol:设置算法的容错范围SSE(簇内误平方差)8 '''

9 kmeans = KMeans(n_clusters=3,init="random",n_init=10,max_iter=300,10 tol=1e-04,random_state=0)11 y_km = kmeans.fit_predict(x)

六、k-means缺陷

k均值算法非常简单且使用广泛，但有一些缺点：

1. K值需要预先给定，属于预先知识，很多情况下K值的估计是非常困难的，因此会有后面的k值确定。

2. K-Means算法对初始选取的聚类中心点是敏感的，不同的随机种子点得到的聚类结果完全不同 。可能只能得到局部的最优解，而无法得到全局的最优解。

3. K-Means算法并不是很所有的数据类型。它不能处理非球形簇、不同尺寸和不同密度的簇。

4. 对离群点的数据进行聚类时，K-Means也有问题。

七、K-Means++

K-Means算法需要随机选择初始化的中心点，如果中心点选择不合适，可能会导致簇的效果不好或产生收敛速度慢等问题。解决这个问题一个比较合适的方法就是，在数据集上多次运行K-Means算法，根据簇内误差平方和(SSE)来选择性能最好的模型。除此之外，还可以通过K-Means++算法，让初始的中心点彼此的距离尽可能的远，相比K-Means算法，它能够产生更好的模型。

K-Means++有下面几个步骤组成：

1、初始化一个空的集合M，用于存储选定的k个中心点

2、从输入的样本中随机选择第一个中心点μ，并将其加入到集合M中

3、对于集合M之外的任意样本点x，通过计算找到与其距离最小的样本d(x,M)

4、使用加权概率分布来随机来随机选择下一个中心点μ

5、重复步骤2和3，直到选定k个中心点

6、基于选定的中心点执行k-means算法

使用sklearn来实现K-Means++，只需要将init参数设置为"k-means++"，默认设置是"k-means++"。

1 km = KMeans(n_clusters=3,init="k-means++",n_init=10,max_iter=300,2 tol=1e-04,random_state=0)3 #y_km中保存了聚类的结果

4 y_km =km.fit_predict(x)5 #绘制不同簇的点

6 plt.scatter(x[y_km==0,0],x[y_km==0,1],s=50,c="orange",marker="o",label="cluster 1")7 plt.scatter(x[y_km==1,0],x[y_km==1,1],s=50,c="green",marker="s",label="cluster 2")8 plt.scatter(x[y_km==2,0],x[y_km==2,1],s=50,c="blue",marker="^",label="cluster 3")9 #绘制簇的中心点

10 plt.scatter(km.cluster_centers_[:,0],km.cluster_centers_[:,1],s=250,marker="*",c="red"

11 ,label="cluster center")12 plt.legend()13 plt.grid()14 plt.show()

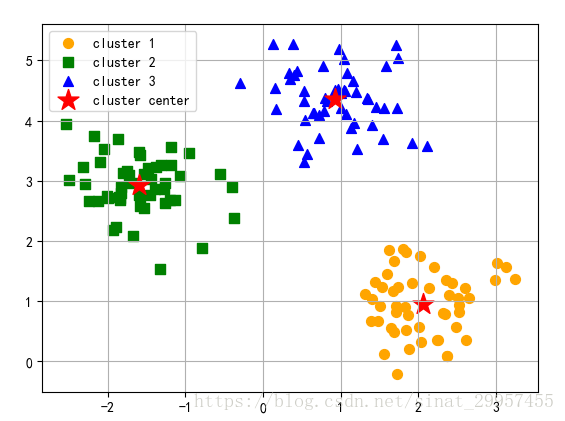
通过上面图可以发现k-means++的聚类效果还不错，簇的中心点，基本位于球心。

使用技巧：

1.在实际情况中使用k-means++算法可能会遇到，由于样本的维度太高无法可视化，从而无法设定样本的簇数。可视化问题可在聚类后显示前用pca对数据降维显示。

2.由于k-means算法是基于欧式距离来计算的，所以k-means算法对于数据的范围比较敏感，所以在使用k-means算法之前，需要先对数据进行标准化，保证k-means算法不受特征量纲的影响。

八、Mini Batch k-Means

在原始的K-means算法中，每一次的划分所有的样本都要参与运算，如果数据量非常大的话，这个时间是非常高的，因此有了一种分批处理的改进算法。

使用Mini Batch(分批处理)的方法对数据点之间的距离进行计算。

Mini Batch的好处：不必使用所有的数据样本，而是从不同类别的样本中抽取一部分样本来代表各自类型进行计算。n 由于计算样本量少，所以会相应的减少运行时间n 但另一方面抽样也必然会带来准确度的下降。

(其他关于k-means的优化还有很多，可参考链接或自行总结)

九、K值的确定

1.根据实际需要

2.肘部法则(Elbow Method)-见后文

3.轮廓系数(Silhouette Coefficient)-见后文

4.层次聚类

层次聚类是通过可视化然后人为去判断大致聚为几类，很明显在共同父节点的一颗子树可以被聚类为一个类

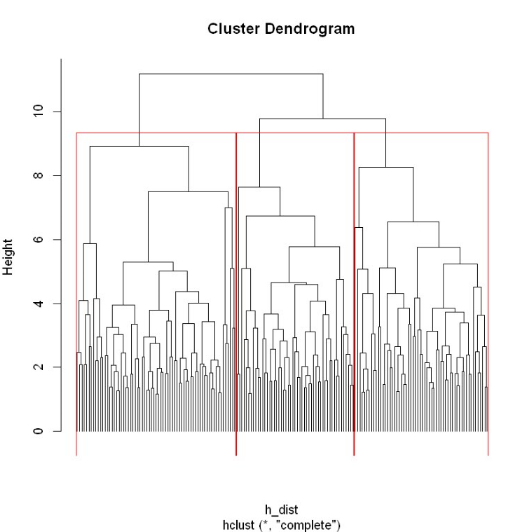
5.Canopy算法

肘部法则(Elbow Method)和轮廓系数(Silhouette Coefficient)来对k值进行最终的确定，但是这些方法都是属于“事后”判断的，而Canopy算法的作用就在于它是通过事先粗聚类的方式，为k-means算法确定初始聚类中心个数和聚类中心点。

与传统的聚类算法(比如K-Means)不同，Canopy聚类最大的特点是不需要事先指定k值(即clustering的个数)，因此具有很大的实际应用价值。与其他聚类算法相比，Canopy聚类虽然精度较低，但其在速度上有很大优势，因此可以使用Canopy聚类先对数据进行“粗”聚类，得到k值，以及大致的k个中心点，再使用K-Means进行进一步“细”聚类。所以Canopy+K-Means这种形式聚类算法聚类效果良好。

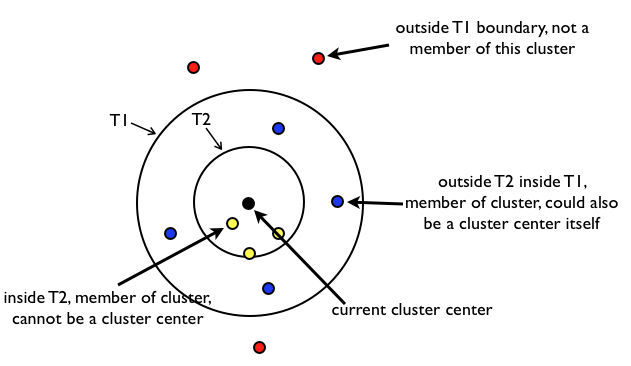
Canopy算法解析：

原始数据集合List按照一定的规则进行排序(这个规则是任意的，但是一旦确定就不再更改)，初始距离阈值为T1、T2，且T1>T2(T1、T2的设定可以根据用户的需要，或者使用交叉验证获得)。

在List中随机挑选一个数据向量A，使用一个粗糙距离计算方式计算A与List中其他样本数据向量之间的距离d。

根据第2步中的距离d，把d小于T1的样本数据向量划到一个canopy中，同时把d小于T2的样本数据向量从候选中心向量名单(这里可以理解为就是List)中移除。

重复第2、3步，直到候选中心向量名单为空，即List为空，算法结束。

算法原理比较简单，就是对数据进行不断遍历，T2

canopy效果图如下：

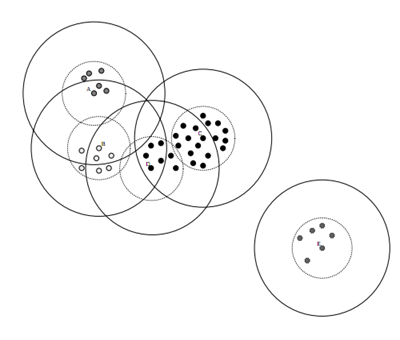
Canopy算法优势：

Kmeans对噪声抗干扰较弱，通过Canopy对比较小的NumPoint的Cluster直接去掉 有利于抗干扰。

Canopy选择出来的每个Canopy的centerPoint作为Kmeans比较科学。

只是针对每个Canopy的内容做Kmeans聚类，减少相似计算的数量。

Canopy算法缺点：

算法中 T1、T2(T2 < T1) 的确定问题(也有专门的算法去描述，但可以自己多次试错

Python实现：

1 #-*- coding: utf-8 -*-

2 importmath3 importrandom4 importnumpy as np5 importmatplotlib.pyplot as plt6

7 classCanopy:8 def __init__(self, dataset):9 self.dataset =dataset10 self.t1 =011 self.t2 =012

13 #设置初始阈值

14 defsetThreshold(self, t1, t2):15 if t1 >t2:16 self.t1 =t117 self.t2 =t218 else:19 print('t1 needs to be larger than t2!')20

21 #使用欧式距离进行距离的计算

22 defeuclideanDistance(self, vec1, vec2):23 return math.sqrt(((vec1 - vec2)**2).sum())24

25 #根据当前dataset的长度随机选择一个下标

26 defgetRandIndex(self):27 return random.randint(0, len(self.dataset) - 1)28

29 defclustering(self):30 if self.t1 ==0:31 print('Please set the threshold.')32 else:33 canopies = [] #用于存放最终归类结果

34 while len(self.dataset) !=0:35 rand_index =self.getRandIndex()36 current_center = self.dataset[rand_index] #随机获取一个中心点，定为P点

37 current_center_list = [] #初始化P点的canopy类容器

38 delete_list = [] #初始化P点的删除容器

39 self.dataset =np.delete(40 self.dataset, rand_index, 0) #删除随机选择的中心点P

41 for datum_j inrange(len(self.dataset)):42 datum =self.dataset[datum_j]43 distance =self.euclideanDistance(44 current_center, datum) #计算选取的中心点P到每个点之间的距离

45 if distance <46>

47 current_center_list.append(datum)48 if distance <49 delete_list.append>

50 #根据删除容器的下标，将元素从数据集中删除

51 self.dataset =np.delete(self.dataset, delete_list, 0)52 canopies.append((current_center, current_center_list))53 returncanopies54

55

56 defshowCanopy(canopies, dataset, t1, t2):57 fig =plt.figure()58 sc = fig.add_subplot(111)59 colors = ['brown', 'green', 'blue', 'y', 'r', 'tan', 'dodgerblue', 'deeppink', 'orangered', 'peru', 'blue', 'y', 'r',60 'gold', 'dimgray', 'darkorange', 'peru', 'blue', 'y', 'r', 'cyan', 'tan', 'orchid', 'peru', 'blue', 'y', 'r', 'sienna']61 markers = ['*', 'h', 'H', '+', 'o', '1', '2', '3', ',', 'v', 'H', '+', '1', '2', '^',62 '', '.', '4', 'H', '+', '1', '2', 's', 'p', 'x', 'D', 'd', '|', '_']63 for i inrange(len(canopies)):64 canopy =canopies[i]65 center =canopy[0]66 components = canopy[1]67 sc.plot(center[0], center[1], marker=markers[i],68 color=colors[i], markersize=10)69 t1_circle =plt.Circle(70 xy=(center[0], center[1]), radius=t1, color='dodgerblue', fill=False)71 t2_circle =plt.Circle(72 xy=(center[0], center[1]), radius=t2, color='skyblue', alpha=0.2)73 sc.add_artist(t1_circle)74 sc.add_artist(t2_circle)75 for component incomponents:76 sc.plot(component[0], component[1],77 marker=markers[i], color=colors[i], markersize=1.5)78 maxvalue =np.amax(dataset)79 minvalue =np.amin(dataset)80 plt.xlim(minvalue - t1, maxvalue +t1)81 plt.ylim(minvalue - t1, maxvalue +t1)82 plt.show()83

84

85 if __name__ == "__main__":86 dataset = np.random.rand(500, 2) #随机生成500个二维[0,1)平面点

87 t1 = 0.6

88 t2 = 0.4

89 gc =Canopy(dataset)90 gc.setThreshold(t1, t2)91 canopies =gc.clustering()92 print('Get %s initial centers.' %len(canopies))93 showCanopy(canopies, dataset, t1, t2)

View Code

6.间隔统计量 Gap Statistic

根据肘部法则选择最合适的K值有事并不是那么清晰，因此斯坦福大学的Robert等教授提出了Gap Statistic方法。

这里我们要继续使用上面的

。Gap Statistic的定义为:

这里

指的是

的期望。这个数值通常通过蒙特卡洛模拟产生，我们在样本里所在的矩形区域中(高维的话就是立方体区域)按照均匀分布随机地产生和原始样本数一样多的随机样本，并对这个随机样本做K-Means，从而得到一个

。如此往复多次，通常20次，我们可以得到20个

。对这20个数值求平均值，就得到了

的近似值。最终可以计算Gap Statisitc。而Gap statistic取得最大值所对应的K就是最佳的K。

Gap Statistic的基本思路是：引入参考的测值，这个参考值可以有Monte Carlo采样的方法获得。

B是sampling的次数。为了修正MC带来的误差，我们计算sk也即标准差来矫正Gap Statistic。

选择满足

的最小的k作为最优的聚类个数。

Python实现：

1 importscipy2 from scipy.spatial.distance importeuclidean3 from sklearn.cluster importKMeans as k_means4

5 dst =euclidean6

7 k_means_args_dict ={8 'n_clusters': 0,9 #drastically saves convergence time

10 'init': 'k-means++',11 'max_iter': 100,12 'n_init': 1,13 'verbose': False,14 #'n_jobs':8

15 }16

17

18 def gap(data, refs=None, nrefs=20, ks=range(1, 11)):19 """

20 I: NumPy array, reference matrix, number of reference boxes, number of clusters to test21 O: Gaps NumPy array, Ks input list22

23 Give the list of k-values for which you want to compute the statistic in ks. By Gap Statistic24 from Tibshirani, Walther.25 """

26 shape =data.shape27

28 if notrefs:29 tops = data.max(axis=0)30 bottoms = data.min(axis=0)31 dists = scipy.matrix(scipy.diag(tops -bottoms))32 rands = scipy.random.random_sample(size=(shape[0], shape[1], nrefs))33 for i inrange(nrefs):34 rands[:, :, i] = rands[:, :, i] * dists +bottoms35 else:36 rands =refs37

38 gaps =scipy.zeros((len(ks),))39

40 for (i, k) inenumerate(ks):41 k_means_args_dict['n_clusters'] =k42 kmeans = k_means(**k_means_args_dict)43 kmeans.fit(data)44 (cluster_centers, point_labels) =kmeans.cluster_centers_, kmeans.labels_45

46 disp =sum(47 [dst(data[current_row_index, :], cluster_centers[point_labels[current_row_index], :]) forcurrent_row_index48 inrange(shape[0])])49

50 refdisps = scipy.zeros((rands.shape[2],))51

52 for j in range(rands.shape[2]):53 kmeans = k_means(**k_means_args_dict)54 kmeans.fit(rands[:, :, j])55 (cluster_centers, point_labels) =kmeans.cluster_centers_, kmeans.labels_56 refdisps[j] =sum(57 [dst(rands[current_row_index, :, j], cluster_centers[point_labels[current_row_index], :]) for

58 current_row_index inrange(shape[0])])59

60 #let k be the index of the array 'gaps'

61 gaps[i] = scipy.mean(scipy.log(refdisps)) -scipy.log(disp)62

63 return ks, gaps

View Code

十、聚类效果评估

1.簇内误方差(SSE)

在对簇的划分中，我们就使用了SSE作为目标函数来划分簇。当KMeans算法训练完成后，我们可以通过使用inertia属性来获取簇内的误方差，不需要再次进行计算。

1 #用来存放设置不同簇数时的SSE值

2 distortions =[]3 for i in range(1,11):4 km = KMeans(n_clusters=i,init="k-means++",n_init=10,max_iter=300,tol=1e-4,random_state=0)5 km.fit(x)6 #获取K-means算法的SSE

7 distortions.append(km.inertia_)8 #绘制曲线

9 plt.plot(range(1,11),distortions,marker="o")10 plt.xlabel("簇数量")11 plt.ylabel("簇内误方差(SSE)")12 plt.show()

可以使用图形工具肘方法，根据簇的数量来可视化簇内误方差。通过图形可以直观的观察到k对于簇内误方差的影响。也可以用来确定K值。

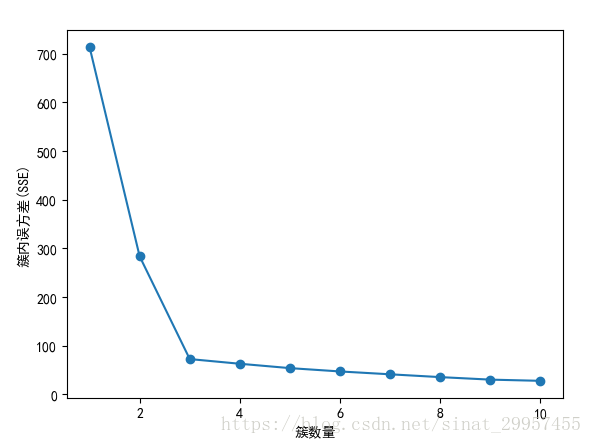
通过上图可以发现，当簇数量为3的时候出现了肘型，这说明k取3是一个不错的选择。但不一定所有的问题都能用肘部法则来解决，如下图右图中，肘部不明显。因此肘部法则只是一种可尝试的方法。

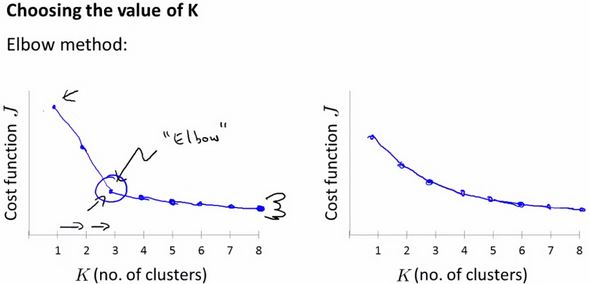
2、轮廓图定量分析聚类质量

轮廓分析(silhouette analysis)，使用图形工具来度量簇中样本的聚集程度，除k-means之外也适用于其他的聚类算法。通过三个步骤可以计算出当个样本的轮廓系数(silhouette coefficient)：

1、将样本x与簇内的其他点之间的平均距离作为簇内的内聚度a

2、将样本x与最近簇中所有点之间的平均距离看作是与最近簇的分离度b

3、将簇的分离度与簇内聚度之差除以二者中比较大的数得到轮廓系数，计算公式如下

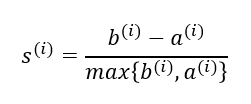
轮廓系数的取值在-1到1之间。当簇内聚度与分度离相等时，轮廓系数为0。当b>>a时，轮廓系数近似取到1，此时模型的性能最佳。

1 km = KMeans(n_clusters=3,init="k-means++",n_init=10,max_iter=300,tol=1e-4,random_state=0)2 y_km =km.fit_predict(x)3 importnumpy as np4 from matplotlib importcm5 from sklearn.metrics importsilhouette_samples6 #获取簇的标号

7 cluster_labels =np.unique(y_km)8 #获取簇的个数

9 n_clusters =cluster_labels.shape[0]10 #基于欧式距离计算轮廓系数

11 silhoutte_vals = silhouette_samples(x,y_km,metric="euclidean")12 #设置y坐标的起始位置

13 y_ax_lower,y_ax_upper=0,014 yticks=[]15 for i,c inenumerate(cluster_labels):16 #获取不同簇的轮廓系数

17 c_silhouette_vals = silhoutte_vals[y_km ==c]18 #对簇中样本的轮廓系数由小到大进行排序

19 c_silhouette_vals.sort()20 #获取到簇中轮廓系数的个数

21 y_ax_upper +=len(c_silhouette_vals)22 #获取不同颜色

23 color = cm.jet(i /n_clusters)24 #绘制水平直方图

25 plt.barh(range(y_ax_lower,y_ax_upper),c_silhouette_vals,26 height=1.0,edgecolor="none",color=color)27 #获取显示y轴刻度的位置

28 yticks.append((y_ax_lower+y_ax_upper) / 2)29 #下一个y轴的起点位置

30 y_ax_lower +=len(c_silhouette_vals)31 #获取轮廓系数的平均值

32 silhouette_avg =np.mean(silhoutte_vals)33 #绘制一条平行y轴的轮廓系数平均值的虚线

34 plt.axvline(silhouette_avg,color="red",linestyle="--")35 #设置y轴显示的刻度

36 plt.yticks(yticks,cluster_labels+1)37 plt.ylabel("簇")38 plt.xlabel("轮廓系数")39 plt.show()

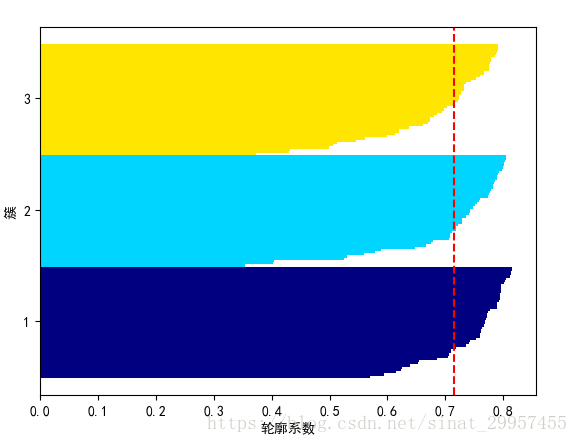
通过轮廓图，我们能够看出样本的簇数以及判断样本中是否包含异常值。为了评价聚类模型的性能，可以通过评价轮廓系数，也就是图中的红色虚线进行评价。

类似SSE，也可以做出不同k值下的效果图：

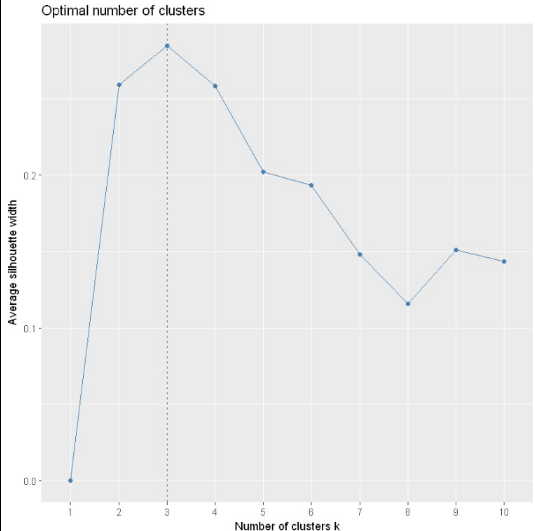
可以看到也是在聚类数为3时轮廓系数达到了峰值，所以最佳聚类数为3

十一、MATLAB实现

最后针对使用MATLAB的给出代码，细节与上文类似：

代码一：

生成随机二维分布图形，三个中心

1 % 使用高斯分布(正态分布)2 % 随机生成3个中心以及标准差3 s = rng(5,'v5normal');

4 mu = round((rand(3,2)-0.5)*19)+1;5 sigma = round(rand(3,2)*40)/10+1;6 X = [mvnrnd(mu(1,:),sigma(1,:),200); ...7 mvnrnd(mu(2,:),sigma(2,:),300); ...8 mvnrnd(mu(3,:),sigma(3,:),400)];9 % 作图10 P1 =figure;clf;11 scatter(X(:,1),X(:,2),10,'ro');

12 title('研究样本散点分布图')

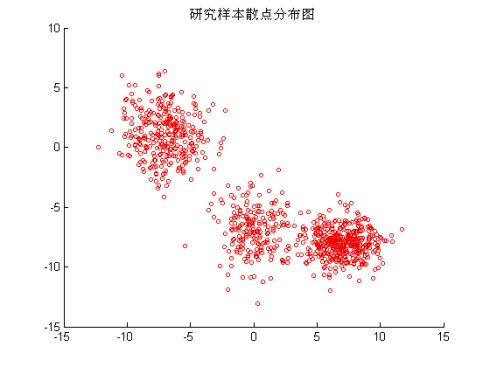
分层聚类：

1 eucD = pdist(X,'euclidean');

2 clustTreeEuc = linkage(eucD,'average');

3 cophenet(clustTreeEuc,eucD);4

5 P3 =figure;clf;6 [h,nodes] = dendrogram(clustTreeEuc,20);7 set(gca,'TickDir','out','TickLength',[.002 0],'XTickLabel',[]);

调用k-means,分成三类

1 [cidx3,cmeans3,sumd3,D3] = kmeans(X,3,'dist','sqEuclidean');

2 P4 =figure;clf;3 [silh3,h3] = silhouette(X,cidx3,'sqeuclidean');

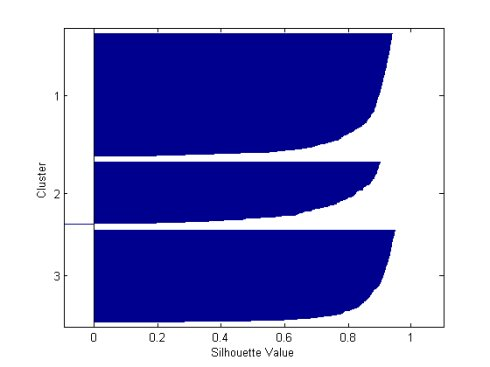
结果显示：

1 P5 =figure;clf2 ptsymb = {'bo','ro','go',',mo','c+'};

3 MarkFace = {[0 0 1],[.8 0 0],[0 .5 0]};4 hold on

5 for i =1:3

6 clust = find(cidx3 ==i);7 plot(X(clust,1),X(clust,2),ptsymb{i},'MarkerSize',3,'MarkerFace',MarkFace{i},'MarkerEdgeColor','black');

8 plot(cmeans3(i,1),cmeans3(i,2),ptsymb{i},'MarkerSize',10,'MarkerFace',MarkFace{i});

9 end

10 hold off

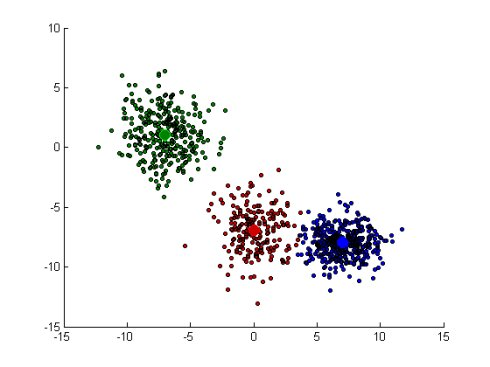
分别用等高线、分布图、热能图和概率图展示结果

1 % 等高线2 options = statset('Display','off');

3 gm = gmdistribution.fit(X,3,'Options',options);

4

5 P6 =figure;clf6 scatter(X(:,1),X(:,2),10,'ro');

7 hold on

8 ezcontour(@(x,y) pdf(gm,[x,y]),[-15 15],[-15 10]);9 hold off

10

11 P7 =figure;clf12 scatter(X(:,1),X(:,2),10,'ro');

13 hold on

14 ezsurf(@(x,y) pdf(gm,[x,y]),[-15 15],[-15 10]);15 hold off

16 view(33,24)17

18

19

20 热能图21 cluster1 = (cidx3 == 1);22 cluster3 = (cidx3 == 2);23 % 通过观察，K均值方法的第二类是gm的第三类24 cluster2 = (cidx3 == 3);25 % 计算分类概率26 P =posterior(gm,X);27 P8 =figure;clf28 plot3(X(cluster1,1),X(cluster1,2),P(cluster1,1),'r.')

29 grid on;hold on

30 plot3(X(cluster2,1),X(cluster2,2),P(cluster2,2),'bo')

31 plot3(X(cluster3,1),X(cluster3,2),P(cluster3,3),'g*')

32 legend('第 1 类','第 2 类','第 3 类','Location','NW')

33 clrmap = jet(80); colormap(clrmap(9:72,:))34 ylabel(colorbar,'Component 1 Posterior Probability')

35 view(-45,20);36 % 第三类点部分概率值较低，可能需要其他数据来进行分析。37

38 % 概率图39 P9 =figure;clf40 [~,order] = sort(P(:,1));41 plot(1:size(X,1),P(order,1),'r-',1:size(X,1),P(order,2),'b-',1:size(X,1),P(order,3),'y-');

42 legend({'Cluster 1 Score' 'Cluster 2 Score' 'Cluster 3 Score'},'location','NW');

43 ylabel('Cluster Membership Score');

44 xlabel('Point Ranking');

View Code

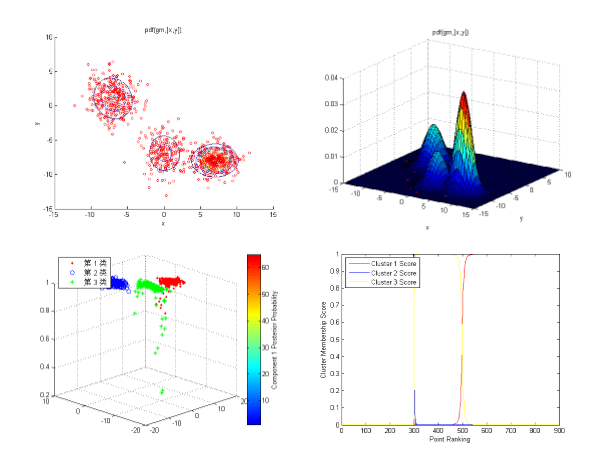
AIC准则寻找最优分类

1 AIC = zeros(1,4);2 NlogL =AIC;3 GM = cell(1,4);4 for k = 1:4

5 GM{k} =gmdistribution.fit(X,k);6 AIC(k)=GM{k}.AIC;7 NlogL(k) =GM{k}.NlogL;8 end

9 [minAIC,numComponents] = min(AIC);

代码二(简单版)：

%随机初始化中心点，可以随机取数据集中的任意k个点

function centroids=kMeansInitCentroids(X, K)

centroids= zeros(K, size(X, 2));

randidx= randperm(size(X, 1));

centroids= X(randidx(1: K), :);

end%对每个点，找到其所属的中心点，即距离其最近的中心点。 返回一个向量，为每个点对应的中心点id。

function idx=findClosestCentroids(X, centroids)

K= size(centroids, 1);for i = 1 : size(X, 1)

min_dis= +inf;for j = 1: K

now_dis= sum((X(i, :) - centroids(j, :)).^2);if now_dis

min_dis=now_dis;

idx(i)=j;

end

end

end

end%用每个中心点统领的那类点的均值，更新中心点。

function centroids=computeCentroids(X, idx, K)

[m n]=size(X);

cnt=zeros(K, n);for i = 1: m

cnt(idx(i), :)= cnt(idx(i), :) + 1;

centroids(idx(i), :)= centroids(idx(i), :) +X(i, :);

end

cnt= 1 ./cnt;

centroids= cnt .*centroids;

end

centroids=kMeansInitCentroids(X, k);for iter = 1: iterations

idx=findClosestCentroids(X, centroids);

centroids=computeMeans(X, idx, K);

end

十二、参考链接：

49>46>