《机器学习》周志华第三章课后习题_试分析在什么情形下式(3.2)中不必考虑偏置项 b

作者：凡人多烦事01 | 2024-04-01 21:19:02

踩

试分析在什么情形下式(3.2)中不必考虑偏置项 b

3.1 试析在什么情形下式(3.2) 中不必考虑偏置项 b.

式3.2
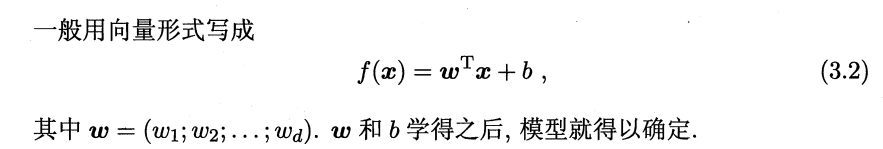
参考网上的各种版本：不考虑偏置项b，那么函数过原点，只需要将训练集的每个样本减去第一个样本，就可以消去b，不必考虑b。

3.2 试证明，对于参数，对率团归的目标函数(3.18) 是非凸的，但其对数似然函数(3.27) 是凸的.

3.18
3.27
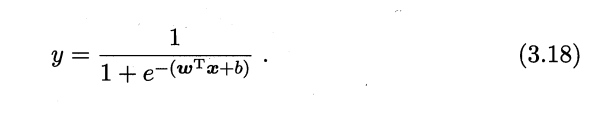
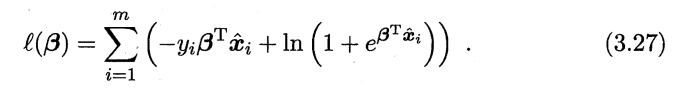
凸函数的定义不是很统一，这里给出西瓜书上使用的定义，P54左下角小字：
凸函数定义
不考虑多元函数时：
对于3.18，用公式推导，证明其非凸，最后会等价为证明 e^(-z)为凸函数；
对于3.27，我的想法是分成两部分来证，第一部分直线，是凸函数；第二部分根据二阶导非负容易证明。两个凸函数相加仍然是凸函数。
考虑多元函数时：如果它是凸函数，则其Hessian矩阵为半正定矩阵。如果Hessian矩阵是正定的，则函数是严格凸函数。只需要证明3.18的Hessian矩阵不定，即存在负的特征值；证明3.27的Hessian矩阵半正定或者正定即可。

3.6 线性判别分析仅在线性可分数据上能获得理想结果?试设计一个改进方法，使其能较好地用于于非线性可分数据

根据课本6.3，可以将非线性可分数据映射到更高维空间，比如，二维映射到三维空间后，可以用平面进行划分。同时引入核函数来简化计算。

3.7 令码长为 9，类别数为 4，试给出海明距离意义下理论最优的 ECOC二元码并证明之.

可以参考论文Solving Multiclass Learning Problems via Error-Correcting Output Codes
根据论文 2.3 Error-Correcting Code Design部分，一个好的ECOC二元码应该满足不同行和不同列之间独立，可以通过增加海明距离来实现，同时不同列之间不互为反码。
论文中给出了四种方法来构造一个好的ECOC编码，3 <= k <= 7时，采用穷举法，参考论文中构造k=5时的做法，构造k=4时的ECOC码如下：

	COL
ROL	1	2	3	4	5	6	7	8	9
1	1	1	1	1	1	1	1	0	0
2	0	0	0	0	1	1	1	1	0
3	0	0	1	1	0	0	1	1	1
4	0	1	0	1	0	1	0	0	1

此时的最小海明距离是4，能够纠正1位。可是，题目中说的是9位，从增加行之间的最小海明距离来考虑，我选择了0110和0011，这样行间最小海明距离就是5。不过，新加的两列是前7列中列的反码，加了反而没好处。

3.8* ECOC 编码能起到理想纠错作用的重要条件是:在每一位编码上出错的概率相当且独立.试析多分类任务经 ECOC 编码后产生的二类分类器满足该条件的可能性及由此产生的影响.

根据书上P65页最后一段文字描述，拆分后产生的二分类任务难度相当，训练生成的二分类器出错概率才会相当；
类别越多，可以产生的编码（组合）也越多，不同二分类器产生编码的海明距离只要足够大，就可以实现，类别越多越可能实现。
影响：一个理论纠错性质很好，但是导致的二分类问题很难的编码，与另一个理论纠错性质差一些，但产生的二分类问题很简单的编码，最终产生的模型性能好坏孰优孰劣很难说。

3.9 使用 OvR MvM 将多分类任务分解为二分类任务求解时，试述为何无需专门针对类别不平衡性进行处理.

根据P66页左侧小字，对于·OVR、MVM来说，由于对每个类进行了相同的处理，类别不平衡问题的影响相互抵消了。

3.10 试推导出多分类代价敏感学习(仅考虑基于类别的误分类代价)使用"再缩放"能获得理论最优解的条件.

太菜了，不会推。。。
答案在周志华老师的论文《On Multi-Class Cost-Sensitive Learning》里，在Analysis 和 The RESCALEnew Approach分别对二分类和多分类的代价敏感问题进行了分析。
在Analysis部分推导出了放缩比公式：
公式3
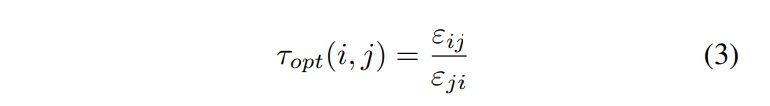
公式的含义：
Generally speaking, the optimal rescaling ratio of the i-th class against the j-th class can be defined as Eq. 3, which indicates that the classes should be rescaled in the way that the influence of the i-th class is τopt(i, j) times of that of the j-th class.
二分类时，传统方法等价与上述方法，多分类时而这并不等价，这解释了为什么传统的放缩方法效果不好。
考虑多分类时的放缩比可以得到下面的式子：

将其转化为线性方程组：
在这里插入图片描述
将其写成矩阵形式：

基于上面的矩阵，得到最优解的条件：当矩阵的秩小于类别数c 时，可以根据方程组求出权重向量w，放缩后的数据可以由非代价敏感分类器处理；否则，将这个多类别问题划分为满足条件的子问题。