- 1巴比特 | 元宇宙每日必读:腾讯将公布大模型和 AI 聊天机器人;阿里妈妈发布两款 AI 新品...
- 2线性表的实现(C语言版)——详细代码_c语言实现线性表
- 3Python爬取京东商品信息以及评论存进MySQL_怎么用python爬去京东的商品信息和价格并存储到mysql
- 4C++中的动态内存管理
- 5程序员怎么升职加薪?十年技术高管的过来人经验!_程序员能升职吗
- 6基于SpringBoot和PotsGIS的各省地震震发可视化分析
- 7【计算机视觉 | 目标检测】术语理解8:模型的实时处理能力,Panoptic Segmentation(全景分割),解耦结构,Anchor-Based,Anchor-Free,特征金字塔网络
- 8又来两款神器,无需魔法直接使用 ChatGPT!_火狐浏览器chatgpt for google怎么用
- 9电脑文件msvcr71.dll丢失的解决方法,4种方法教你速度修复msvcr71.dll_msvcp71.dll
- 10LLM大语言模型:为数据分析师提供自然语言处理能力_llm和nlp的关系
ANN人工神经网络:从基础认知到现实理解_如何理解神经网络的输入层、隐含层和输出层
赞
踩
什么是神经网络?
神经网络的再认知
前面我们了解过,人工神经网络(Artificial Neural Network,ANN)是人类为了模仿人大脑的神经网络结构创建出来的一种计算机系统结构。但如果仔细深入到神经网络当中,会慢慢发现还可以更加深入理解神经网络是什么。
神经网络一般有三层,分别为输入层、隐藏层、输出层:
- 第一层:输入层:数据由此输入进入神经网络;
- 第二层:隐藏层:数据输入呈现给网络后,由此处开始数据的变化,变化成可以由输出层可以理解(需要)的内容。隐藏层可以有多个,除了输入输出层,其余的都是隐藏层。
- 第三层:输出层:神经网络运算结果,或是分类结果。
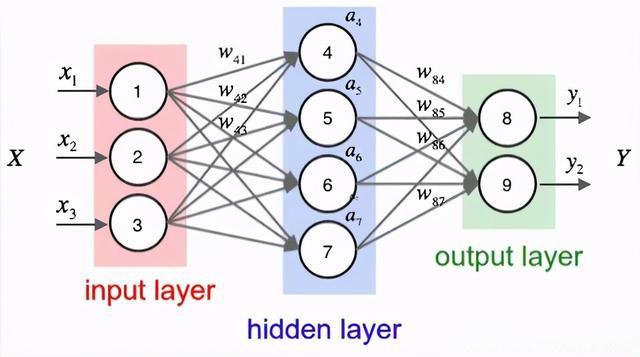
通俗理解神经网络
这么说你肯定会懵圈,那么我们如何通俗理解神经网络?
实际上,机器学习或者说神经网络最擅长解决的问题就是分类,无论是计算机视觉检测、语言识别和现今大流行的无人驾驶,其核心都可以归结为对数据的有效分类。而神经网络的本质,可以理解为候机楼发生的一系列场景故事,这过程包含了登记前的各种排队、检查和分流,目的就是把我们安全的送上飞机。
那么,如果把候机楼比作是一个神经网络,而来机场的人是输入,最终的航班则是输出类别,神经网络要解决的就是如何让人们有效地办理登机手续。登机手续、安检、验票、查护照、过海关、登机一系列的流程下来,说白了就是候机楼的流程设计。
现在让我们假设需要登上一架飞机的流程。
-
无论我们的人从哪里来,在办理登机手续过程当中都需要汇聚成一条直线的队伍进行排队登机。用数学语言描述来说,这是“线性叠加”, y = ∑ i = 1 i w i x i + b y = \sum_{i=1 }^{i} w_ix_i+b y=∑i=1iwixi+b,这就是我们初中学过的直线方程,其中 w w w是斜率, b b b是截距。
-
可如果人太多,队伍太长不方便,这个时候我们就需要将队伍拐个弯?行话里叫做——“加入非线性”,抽象成数学语言里来说,就是把上面的直线方程代入到一个叫做——“激活函数 y = f ( ∑ i = 1 i w i x i + b ) y = f(\sum_{i=1 }^{i} w_ix_i+b) y=f(∑i=1iwixi+b)” 里,而这个就叫做神经元模型。(也有称之为“感知机”),在神经元模型中, w w w表示权重, b b b则表示参数。
如同队伍可以排成一条折线、曲线,常见的激活函数既有折线形的ReLu函数,
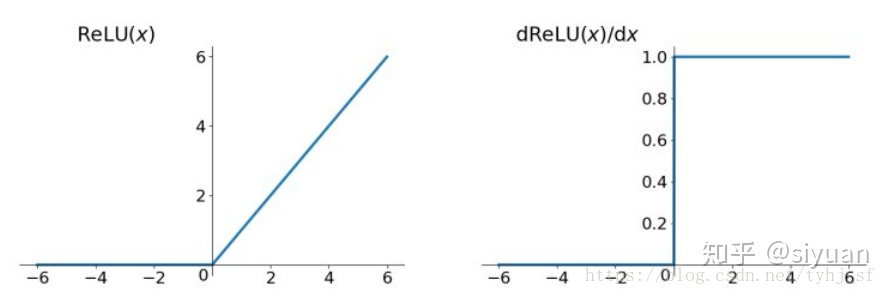
也有曲线型的Sigmoid、tanh函数等等。
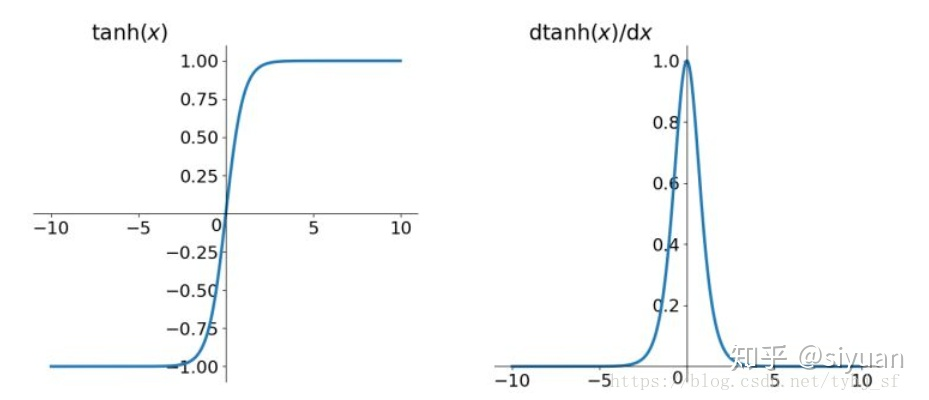
说白了,激活函数的作用就是在改变队伍的队形。常见的激活函数有10种,可以点击链接去了解,在实际运用起来会发现ReLu函数最方便和有效。而Relu函数图像,更可以理解成生活中可以自由分隔队形的隔离柱。
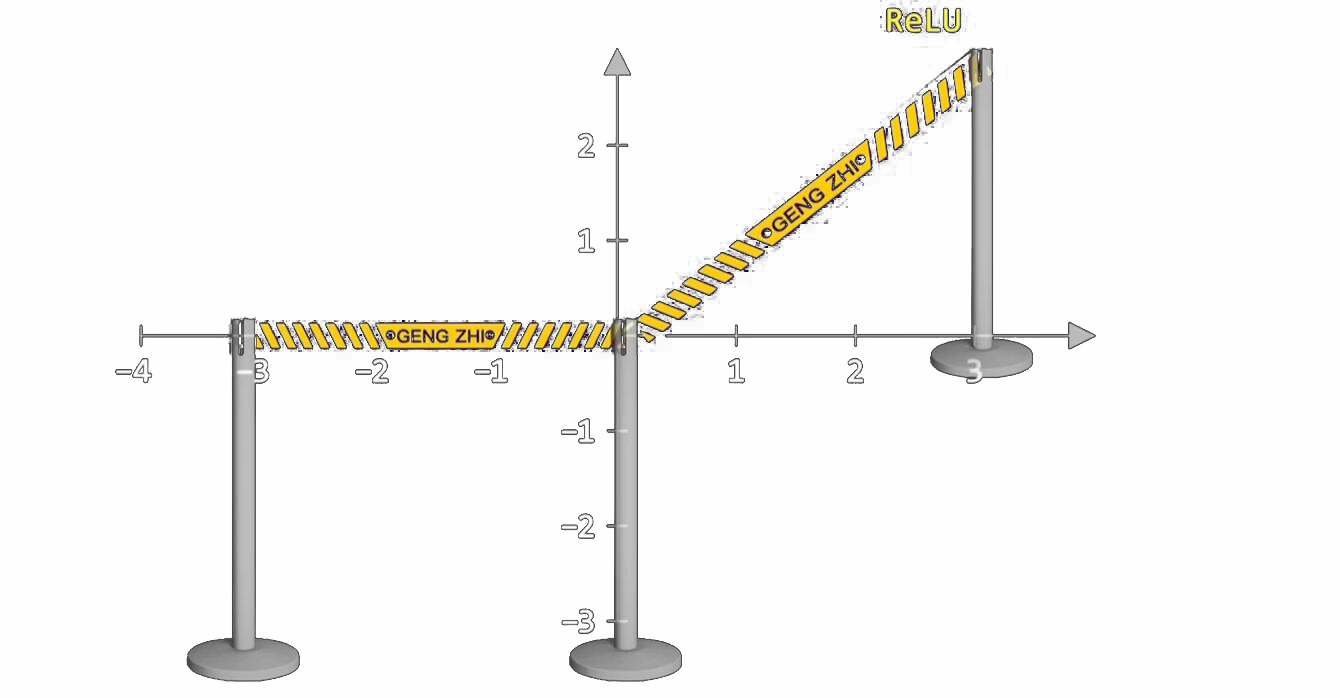
如同用多个隔离柱前后相连可以组成弯弯曲曲的隔离带,多个神经元团结起来及内在效果就是形成折线形的分类线,用于规范从输入到输出的之间过程的分类,而前面说的 y = f ( ∑ i = 1 i w i x i + b ) y = f(\sum_{i=1 }^{i} w_ix_i+b) y=f(∑i=1iwixi+b) 提到的 权重 w w w和参数 b b b起到的作用就如同隔离柱摆放的角度和位置
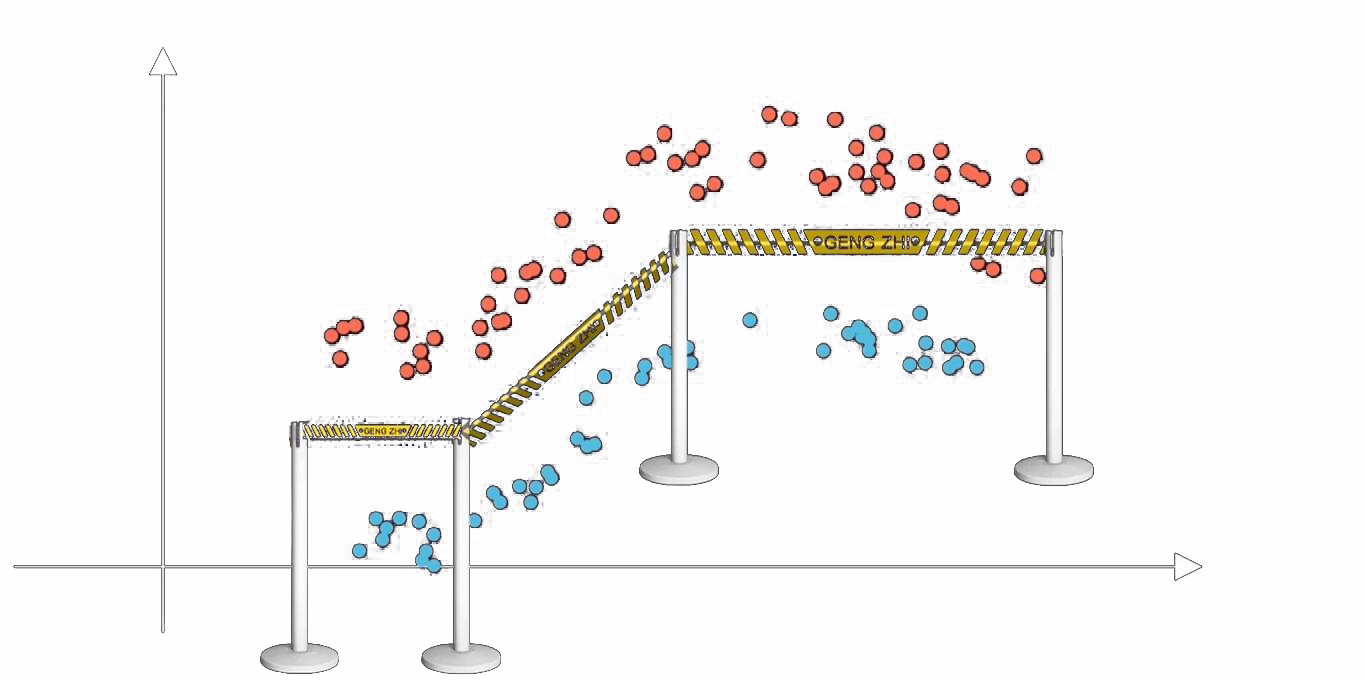
无论有多少个登机口,一直用隔离带分割队形就完事。类比过来单层神经元就可以解决一个问题了,那为什么一个神经网络需要多个隐藏层呢?
那么可以再来想想候机楼的情景,当我们登记前,入口需要做防爆检查排队、打印登机牌需要排队、检票要排队、登机要排队、取行李要排队,而这每个过程是不是旅客先聚集,再分类和分流呢?因为大家的起飞到达时间和行李到达情况都是有所不同的,而在机场的每个步骤不同机构都是对身份、安全、行李、证件等关注点各不相同,这就是为什么需要多层神经网络的原因了。
把前一层的输出当成后一层的输入,分成不同的步骤分分合合在神经网络空间内进行变换,说到底神经网络就像候机楼一样在对输入数据进行分类流程的设计。
数学的角度理解神经网络
为了找出机票价格与起飞时间的关系,在一个二维坐标系上,X轴是机票的价格,而Y轴是飞机起飞的时间,神经网络的目的就是找到它们之间的最佳分类线。
简单情况下一个神经元就够了,而在复杂情况下可能就需要多个神经元、多层结构以便设计更加有效的分类线,例如将一个二维数据转换为三维空间变化,从而找出它们之间的最佳分类线。
当输入的数据是更高维度时,神经网络代表的就不再是分类线而是分类面,变来变去的核心思想和原理还是不变的:
- 通过神经元(激活函数)升维,增加线性转换能力;
- 通过多个隐藏层,增加非线性转换次数。
这就是神经网络的原理与奥秘。
如同生活中的机场,人流量和吞吐量不断变大,机场也在不断扩建,神经网络也从最初的几层逐步扩展到几十层、乃至上百层,由成千上万个神经元形成所谓的深度神经网络。
古人云:“凡是过犹不及“。那么过于复杂的设计往往带来的就是效率低下,在一些大型机场内,人们总感觉是走在迷宫当中找不到方向,这在行话里叫做——过拟合(”Over fitting")。那么如何处理呢?如同大型机场会对不同乘客提供贵宾通道、VIP候机区、急客通道等等,神经网络领域的研究者也挖空心思做了同样的事情,先后提出了卷积神经网络CNN,循环神经网络RNN等各种结构,以及在它们的基础之上进行各式各样的变体,不断优化设计、提升效率。
1998年,法国学者Yann LeCun将卷积运算与神经网络相结合,提出了著名的卷积神经网络模型(Convolution Neural Network CNN卷积神经网络 )。
什么是卷积?
上至天文物理,下至工程科学,再到生活中无处不在的信号处理人工智能,卷积在过去的几十年里不断开疆扩土,大放异彩,几乎已经成为各类研究和应用的必备工具。它令无数科学家爱不释手,却又让很多初学者倍感困惑,于是遍有了说卷积是种看待世界的方式。接下来,我们来了解什么是卷积。
卷积的释义
首先,什么是卷积?卷积的英文名是—— Convolution。其中,con是共同的意思,也可以理解成”积分“;词根vol,是卷和转的意思;整个词组成了既卷,又积的意思,这就是卷积一词的释义来源。
卷积的数学公式
卷积的连续性数学公式是:
(
f
∗
g
)
(
t
)
=
∫
−
∞
∞
f
(
τ
)
g
(
t
−
τ
)
d
τ
(f*g)(t)=\int_{-\infty }^{\infty}f(\tau )g(t-\tau)d\tau
(f∗g)(t)=∫−∞∞f(τ)g(t−τ)dτ
其中包含了:
- $f(\tau ) $ 中的 ( τ ) (\tau) (τ) 和 g ( t − τ ) g(t-\tau) g(t−τ)中的 ( t − τ ) (t-\tau) (t−τ) 表示了旋转(卷和转)
- f ( τ ) g ( t − τ ) f(\tau )g(t-\tau) f(τ)g(t−τ)的相乘
- ∫ − ∞ ∞ \int_{-\infty }^{\infty} ∫−∞∞积分
- 其中,卷积运算符号用星号 * 来表示以此区分普通的乘法。
这3个步骤组成了卷积的过程。
那么,这个卷积到底是做什么呢?网上有很多帖子都在介绍卷积,但变换、旋转、积分等这些奇幻的词汇在初学者看来太过深奥,有的一上来就列举一堆数学公式定理,要是初学者都能是初学者该多好。也有的帖子在列举生活中的例子,例如:掷骰子、信号分析等等,但又有一种未触及本质隔靴搔痒之感,接下来,让我们来一起揭开它的神秘面纱,透视其美妙之处。
如何理解卷积
卷积本质上还是种运算,只不过比常见的加减乘除要高级很多。如果用一句人话来介绍:卷积用极简的数学形式漂亮的描述了一个动态过程。
什么样的动态过程?接下来我们以火车进山洞为举例:
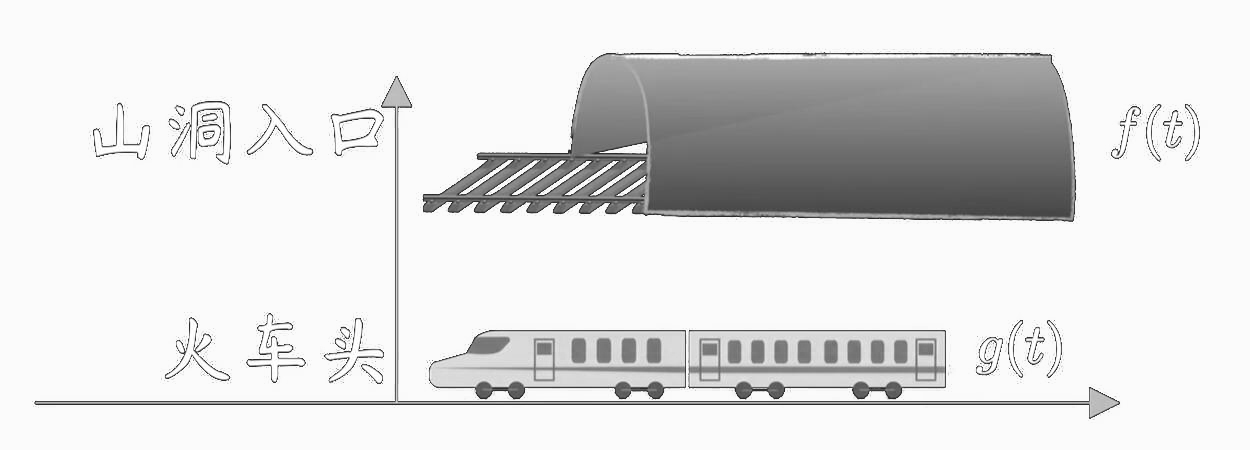
假设现在有一个火车和一个山洞
- 令火车为 g ( t ) g(t) g(t), 山洞为 f ( t ) f(t) f(t)
- 它们两个同时摆在一个坐标轴上,且整体都位于坐标轴的右侧。
- 特别的,它们的头部和入口处,都位于坐标轴上的相对位置的左侧(头和入口都是第一象限的左侧);
现在要如何描述火车进入山洞的过程呢?
首先,我们是不是需要把车头对准山洞口,然后再一点点山洞,最后一点点驶入山洞?这个过程就是卷积要解决的问题。
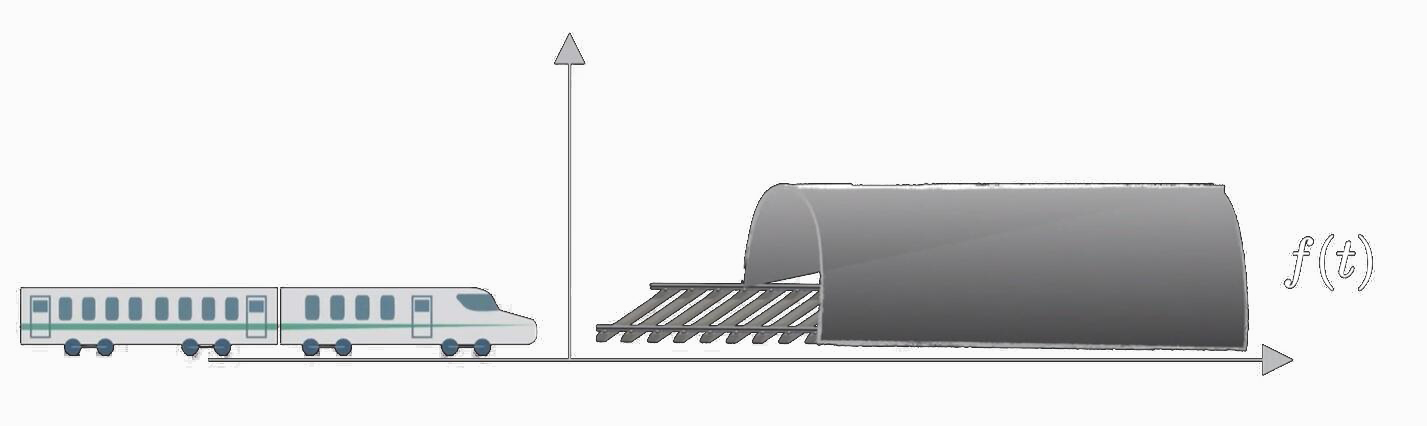
用数学语言来说:
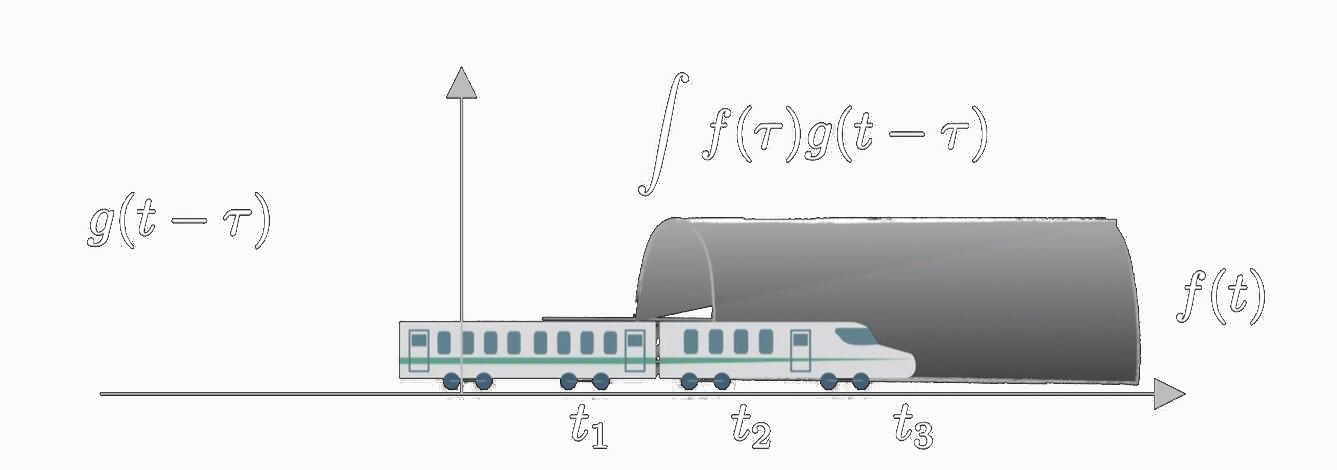
- 把火车翻转过来,就是把火车的 g ( τ ) g(\tau) g(τ) 变成 g ( − τ ) g(-\tau) g(−τ),由此实现车身的翻转。
- 那么该如何让火车动起来呢?用时间变量 t t t 表示全局时间的变化,便有了 $ g(t-\tau) $ 描述火车的随着时间变化的运动趋势。
- 此时,将 $ g(t-\tau) $ 与 f ( τ ) f(\tau) f(τ)乘积,表示火车进入山洞后每一时刻火车与山洞两者相对的位置。其中全局时间变量 t t t的用 t 1 t_1 t1, t 2 t_2 t2 , t n t_n tn表示。
- 积分 ∫ − ∞ ∞ \int_{-\infty }^{\infty} ∫−∞∞,也就是累加和,则记录了火车进入山洞后二者不断重叠,互相作用的过程。
现在,我们如何理解它与卷积之间的关系呢?
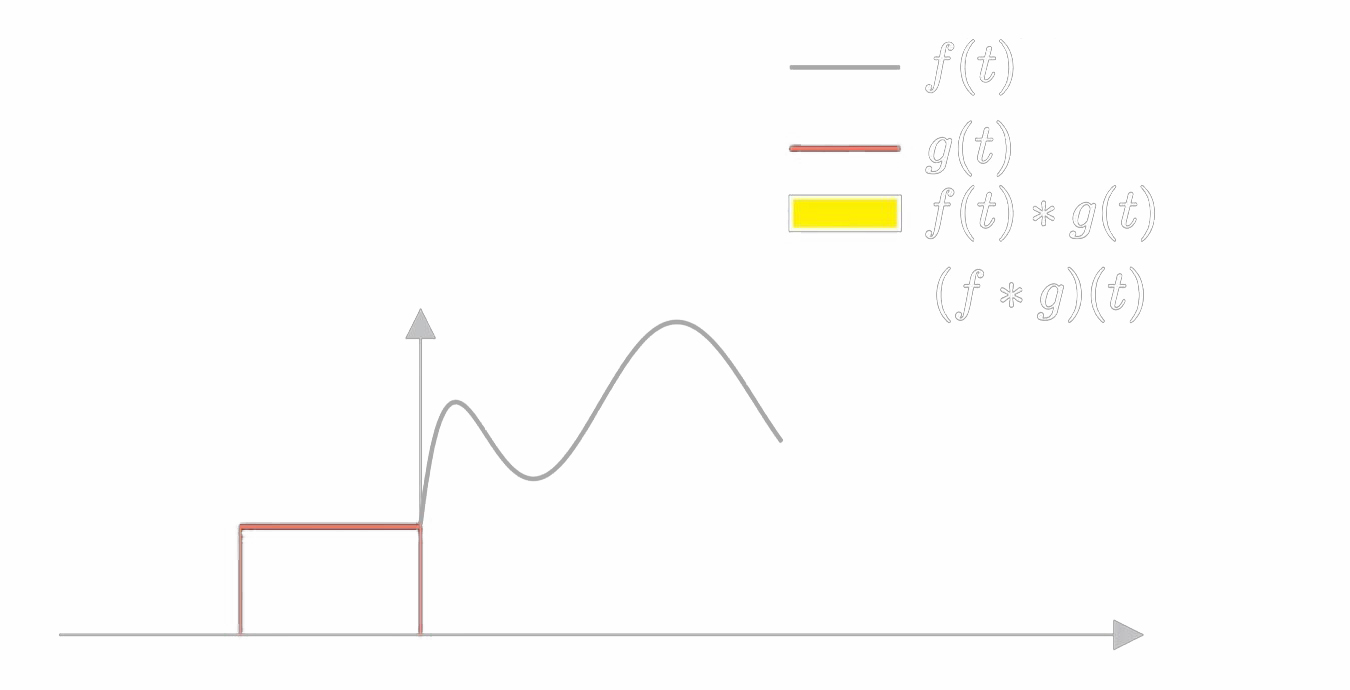
现在,我们把火车和山洞理解成函数曲线。
- 现在我们假设其中,红色块表示火车,弯曲的曲线表示山洞。
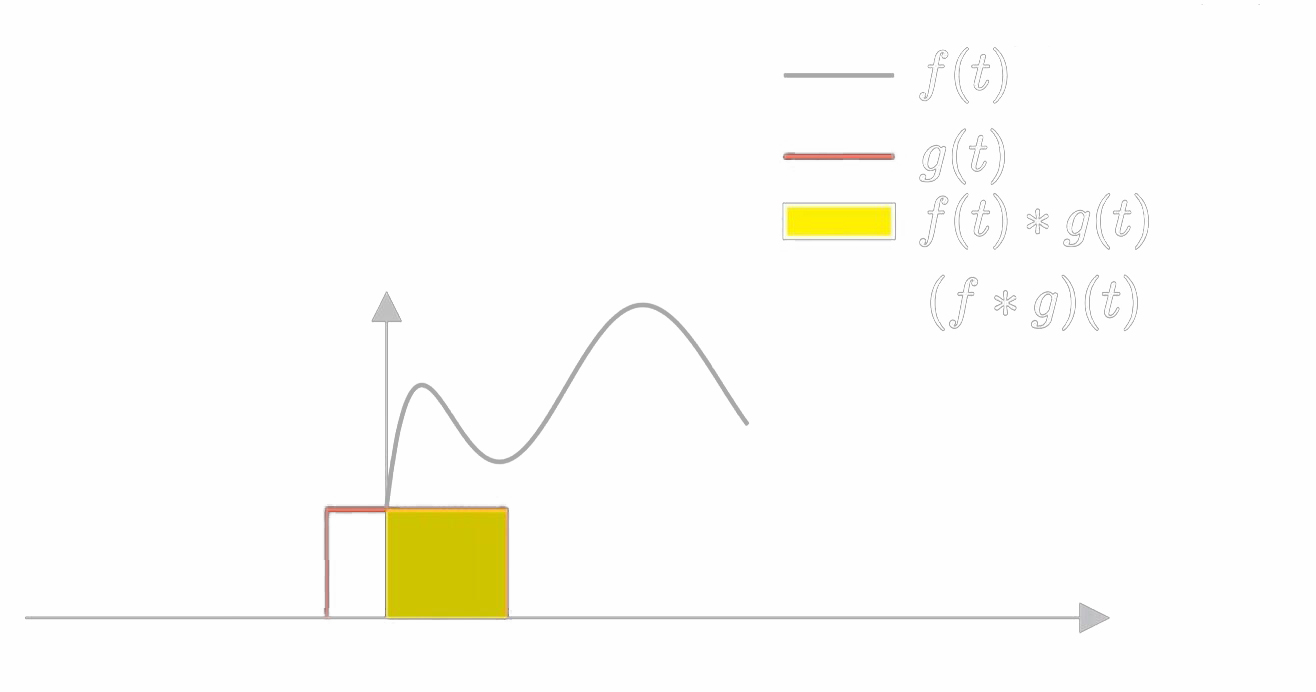
- 两个函数图像重叠交汇的面积,用黄色区块表示
当代表火车的红色块进入到山洞里的弯曲函数曲线时,此时两个函数重叠的黄色区块就是传说中的卷积 f ( t ) ∗ g ( t ) f(t) * g(t) f(t)∗g(t)。
另外的,代表火车和山洞的 f f f和 g g g可以是各种弯弯曲曲的形式,因为卷积表达的就是“一个函数与另外一个函数交叉重叠的动态过程”(函数f钻入函数g的动态过程)这也就是卷积一词里的 Con。因为要从头部开始进去,所以必须要把一个函数翻转旋转才能进入,这就是卷积里的 vol (卷、转、旋转)。同时,这两个函数的身份是可以互换的:**函数 f f f 进入 函数 g g g ,也可以是函数 g g g 进入 函数 f f f. (火车进山洞,山洞套火车)。**而积分的目的,就是求出这两个函数交汇重叠的面积,这也叫做——“卷积交换性质”。
那么离散型的视角来看,就有了卷积的离散型公式: ( f ∗ g ) ( n ) = ∑ τ = − ∞ ∞ f ( τ ) g ( n − τ ) (f*g)(n)=\sum_{\tau=-\infty }^{\infty}f(\tau)g(n-\tau) (f∗g)(n)=∑τ=−∞∞f(τ)g(n−τ)
什么是卷积神经网络?
伴随着21世纪海量互联网大数据和GPU等硬件设备的快速发展的崛起,深度卷积网络自2012开始一炮而红,引领了过去十年间的人工智能技术的再度崛起,在众多领域显示了超越人类的强大能力。那么,到底什么是卷积神经网络呢?
卷积神经网络最早运用在计算机视觉领域,我们现在耳熟能详的人脸识别、字符识别还有各种相机美颜,背后算法的核心都是CNN技术 。
一个卷积神经网络往往由“卷积层——池化层——全连接层”组成。接下来我们来了解这每一层的作用和意义。
卷积层
为什么需要卷积层?
回顾一下神经网络模型

其中,节点代表神经元,连线则表示神经元之间的计算关系,每条线都有自己对应的权重关系,每层节点都和上一层的所有节点相连,构成的就是全连接神经网络。所谓的学习训练就是为了调整权重使得它的效果细化,调整的过程同时过程来讲就是喂数据——吃饭长身体的过程。
从审美的角度来看,神经网络模型就像是一个好吃懒做的大胖子,看似身材高大(结构密密麻麻),其实一身肥肉不结实(冗余度大)。这种提醒常常是吃得多,消化能力差,空有一身赘肉显得特别笨重。用学术上来说就是:“参数众多,难以训练。”
举个例子,如果输入一张“100x100"长度大小的图像进行训练,即使在忽略bias偏离率情况下进入全连接层时,每个神经元还会有10000个权重参数,这过程非常容易产生过拟合的情况,换言之就是吃多了容易吃出毛病。而卷积的过程,就是在调参,使得这过程更加细化,而卷积放在例子当中,就是一个精干挑剔的另一半,立志改善你的生活习惯使你成为一个高质量人类。话不多说,我们开始进入卷积神经网络!
卷积神经网络:卷积的过程
引入
我们知道,在视频中的影像实际上是一组图片以极快的方式交替展现的,其中的每一张图片叫做一帧,而在做图像识别时,卷积神经网络就是应用在这样的一帧图像上的。另外的,我们看到的图片实际上是由RGB(Red Green Black)或其他颜色模型下多种颜色图像堆积叠加而成的,每种颜色从浅到深,又分为0-255一共256个等级的颜色等级。
每当卷积神经网络要把图片交给神经网络之前,总是先要对图像进行卷积的操作,那操作步骤该是如何做的呢?
什么是卷积核?
由引入所提,图片的是由颜色堆积而成的,如何让计算机用新的一种方式表示图像是一个问题?矩阵是一个不错的思路,我们可以把图片转化为数字的矩阵。
接下来,为了提取图像的特征,我们会构建一个正方形的点阵,这个点阵就叫做卷积核。
当我们在看到一张图时,会不由自主的去观察它们之间的特征。我们以字母 “X"为例:

通过细心观察我们可以发现它具有3个典型的局部特征,分别是两种斜对角线和一种十字交叉型。



既然观察到这种特征,那么我们就可以请出我们的卷积核来进行操作。
我们首先将原始的字母矩阵化,把黑色区域的图像信息标记成1,白色区域为-1,这样就可以用矩阵表示出原始图像了。
此时我们需要构建一个具有相同特征的小矩阵,这里的矩阵可以统称为”卷积核“
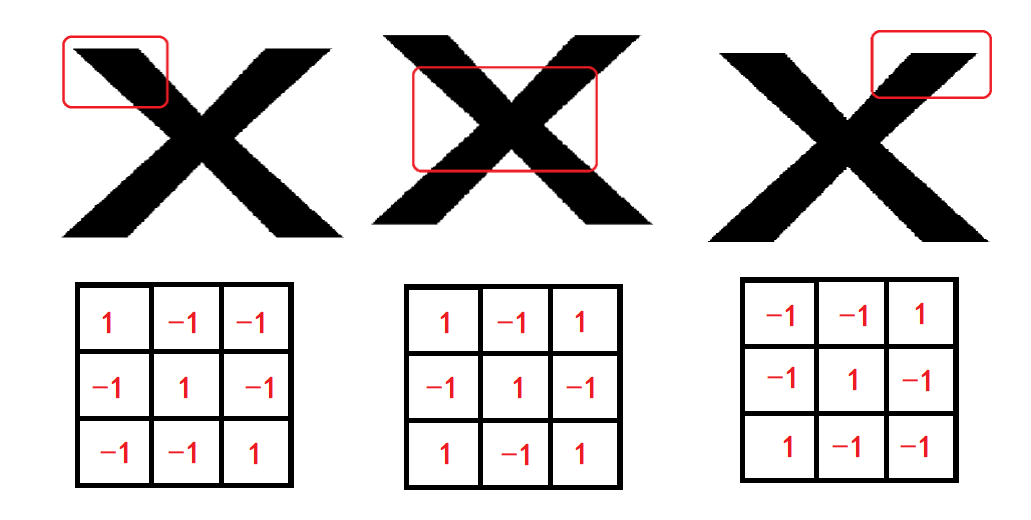
用卷积核扫描原始图像,将与原始图像的对应位置的元素相乘后相加,用一个新的矩阵记录计算后的值。
这个过程,用数学式子表达,就是二维离散卷积操作。
y [ n 1 , n 2 ] = x [ n 1 , n 2 ] ∗ h [ n 1 , n 2 ] = ∑ m 1 = − ∞ ∞ ∑ m 2 = − ∞ ∞ x [ m 1 , m 2 ] ⋅ h [ n 1 − m 1 , n 2 − m 2 ] y[n_1,n_2] = x[n_1,n_2] * h[n1,n2]=\sum_{m_1=-\infty }^{\infty}\sum_{m_2=-\infty }^{\infty}x[m_1,m_2] · h[n_1-m_1,n_2-m_2] y[n1,n2]=x[n1,n2]∗h[n1,n2]=m1=−∞∑∞m2=−∞∑∞x[m1,m2]⋅h[n1−m1,n2−m2]
上述的操作就是图像卷积的过程。
卷积的意义
前面我们提到,卷积操作实际上就是用一个输入 乘以 系统函数,然后计算输出。在图像处理中,输入就是原始图像的像素,系统函数就是卷积核,这也是卷积神经网络的名称由来。
这时候你可能会想问,卷积操作的意义何在呢?上面说到,卷积是为了提取图像的关键信息,从而为之后的神经网络计算创造更好的条件,而这里的卷积核也常常被称作为“过滤器”。
那么卷积的实际意义就是在于通过二维的离散卷积操作,把一个全连接的神经网络变成一个小小的局部链接,实现了高效的图像特征提取。在例子中我们发现,无论关键特征在哪卷积核总能找出这个特征点的所在位置,而这就是小小的卷积核具备的一项特殊功能—“空间特征平移不变”。
无论图像大小如何,通过卷积操作,每个滑动扫描的区域都具有相同共享的权重值,如果使用3*3大小点阵的卷积核,在忽略bias偏离率情况就只需要学习9个参数,从10000个参数到9个参数,香不香?换在我们前面比喻全连接神经网络的一个肥胖的胖子,卷积的出现就像是找到一个挑剔的另一半,从根本上关注他的嘴,精挑细选了每日的饭量而养成良好饮食习惯,同样饭量下,消化能力当然会显著增强。
卷积运算得到的得到的结果矩阵往往被称作——“特征图(feature map)”,特征图上的每个点都是由上一层的若干个点共同计算得出的。比如3*3卷积核中,每个点是由上一层的9个点决定的,我们可以把这9个点称之为——“感受野”。那么可以想象一下,卷积网络层数越多,每一点的感受野越大,而感受野越广阔,就越能够捕捉更大尺寸的特征。通常下,一层卷积不过瘾层层叠加起来才到胃,这就是所谓的深度卷积网络。
科学家们发现,卷积层数越多,对复杂特征的表达能力越强,几层只是毛毛雨,十层不嫌多,成百上千层刚刚好。
以图像分类为例,现在要对字母“X”进行3层的简单卷积操作
- 第一层,可以通过对特定位置的角度是否出现边缘的


第二层:则是可以将这项边缘组合化;

第三层:组合成物体特征部位的模式;

这样的逐级学习下去,就能学习到图像的特征了
回到之前的例子,哪个另一半只会关心你的几顿饭的饮食呢?真正的关心是周期性、多尺度和全面的,除了饮食,她肯定也很关注你的人品、能力,谁不想要一个德智体美劳全面发展的另一半呢?OWO
卷积层的激活函数
神经网络之所以能够解决非线性问题,本质上就是加入了激活函数的这一非线性因素到里面,否则就和线性回归区别不大了。卷积神经网络也不例外。
卷积神经网络在卷积过后也加入了激活函数,最常用的是线性整流单元(Rectified Linear Unit)简称ReLu函数
R
e
L
u
(
x
)
=
m
a
x
(
x
,
0
)
ReLu(x) = max(x,0)
ReLu(x)=max(x,0)

听着这个名字是不是很炫?根据函数图像会发现,其实这个函数就是把特征图上的所有负数都变成0,而整数不变。作为优秀的你应该很好理解这个选择,既然挑剔的卷积另一半帮你辨别了习惯的好坏,当然要把所有坏的都改掉并让它们都变成0,别死磕一根筋。这就是非线性激活函数的真谛。
以上就是卷积层的全部操作了,接下来我们来了解池化层吧。
池化层
所谓的池化层,英文释义是——Pooling,本意如果翻译成淤积、汇聚会更容易契合池化层的理解。这一层的作用说直白点就是抓住主要矛盾,忽略次要因素。
池化层是把局部多个神经元的输出组合成下层单个神经元来减少数据维度。
用数学语言描述,就是在一个小矩阵中找最大值或者平均值,这就是所谓的最大池化或者平均池化运算。
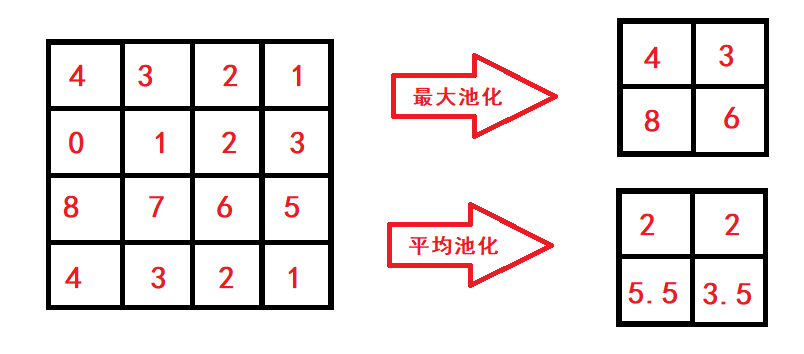
池化层的意义
卷积层后跟着一个池化层,其主要目的就是为了进一步放大图像特征,而忽略掉几个像素的偏差,其意义不光能降低数据维度从而减少训练参数,同时还能够避免所谓的过度拟合。
作为优秀的你,在初次和别人交流认识时,尽量把自己的优点放大,自己一些细小的缺点蒙混过关就好了,这就是池化层的意义。
全连接层
卷积神经网络的最后一层往往都保留一个全连接层。
与传统神经网络一样,它会把相邻两层的神经元全部交叉相连,其作用好比从全局出发做最终的结论。和前面的卷积层搭班子形成了先局部再整体的学习结构。
全连接层的意义
卷积加池化,多层集连,对输入数据进行多尺度特征提取和深度学习。这就好比挑剔的卷积另一半挑毛病+你的主动自省的反复上演,曾经臃肿的全连接神经网络终于在挑剔的卷积另一半的帮助下成功瘦身成为一名吃的少挣的多、学习能力强、思考有深度的高质量人类。 这就是卷积神经网络成功的秘诀
卷积神经网络的发展和演变
卷积和神经网络的第一次相遇发生在计算机视觉领域
- 第一个红娘就是:日本学者福岛邦彦,1980年他受前人关于生物视觉系统研究的启发,提出了层级化的人工神经网络,即神经认知模型处理手写字符识别问题。这被认为是卷积神经网络的前身。不过这最多只算是卷积和神经网络的第一次牵手。而二人的真正的合体是法国学者——杨立坤等人。
- 法国学者杨立坤等人在1998提出基于梯度学习的卷积神经网络算法LeNet,它被广泛应用于美国邮政系统的手写数字和字符识别。
- 卷积神经网络的第一次大放异彩要回溯到2012年著有计算机视觉界世界杯之称的ImageNet竞赛上,Hinton等人凭借AlexNet一举夺魁。这个网络的结构和LeNet非常相似,但是更深更大,并且使用了层叠的卷积层来获取特征。超高的识别率让学术界意识到,卷积对神经网络改造的巨大潜力。
- 之后Google、Facebook、微软以及国内的BAT等公司纷纷投入巨资研究,各种变体的卷积神经网络层出不穷,例如ZFNet,通过可视化展示了卷积神经网络各层级的功能和作用,牛津大学提出了VGGNet,采用了堆积的小卷积核和代替大的卷积核,不仅能够增加决策函数的判别性,还能减少参数量。GoogleNet增加了卷积神经网络的宽度,使用1*1卷积降维,减少参数量,在多个不同尺度的卷积核上进行卷积后再聚合。ResNet残差网络,解决了网络模型的退化问题,使得神经网络可以更深。
总的来说,卷积神经网络越变越宽,越来越深,越来越复杂。就像卷积和神经网络两人的爱情故事一样愈发浓烈、深刻和多元。卷积神经网络也从最初开始的计算机视觉领域快速拓展到语音识别、自然语言处理等领域,进而运用到工程科学的各行各业,但不管怎么变,CNN的核心思想都没有变——利用卷积核的特征提取能力,通过多层级联、实现多尺度特征学习。换句话来说,就是充分调动卷积另一半的积极性,进而让神经网络这孩子激发出巨大潜力。
函数的判别性,还能减少参数量。GoogleNet增加了卷积神经网络的宽度,使用1*1卷积降维,减少参数量,在多个不同尺度的卷积核上进行卷积后再聚合。ResNet残差网络,解决了网络模型的退化问题,使得神经网络可以更深。
总的来说,卷积神经网络越变越宽,越来越深,越来越复杂。就像卷积和神经网络两人的爱情故事一样愈发浓烈、深刻和多元。卷积神经网络也从最初开始的计算机视觉领域快速拓展到语音识别、自然语言处理等领域,进而运用到工程科学的各行各业,但不管怎么变,CNN的核心思想都没有变——利用卷积核的特征提取能力,通过多层级联、实现多尺度特征学习。换句话来说,就是充分调动卷积另一半的积极性,进而让神经网络这孩子激发出巨大潜力。