支持向量机检测DGA_使用支持向量机进行缺陷检测

先来介绍支持向量机。
其英文全称是Support Vector Machines。支持向量机是我们用于分类的一种算法。支持向量机 (SVM) 是一个非常经典且高效的分类模型。但是，支持向量机中涉及许多复杂的数学推导，并需要比较强的凸优化基础，在参考链接中读者可以参考相关文章，学习从零推导SVM，这里仅以简单地图示帮助大家了解。
在SVM中，选择超平面以最佳地将输入变量空间中的点与它们的类（0级或1级）分开。超平面是纯粹的数学概念，不是物理概念，它是平面中的直线、空间中的平面的推广，只有当维度大于3，才称为“超”平面。
SVM的核心任务就是：构建一个N-1维的分割超平面来实现对N维样本数据放入划分，认定的分隔超平面两侧的样本点分属两个不同类别。
以简单的二维平面为例进行介绍

A、B、C三条直线哪一条才是正确的分类边界呢？显而易见，只有A“完整”的区分了两种数据的决策边界。

上图中，A、B、C三条线都完整的区分了边界，那我们应该如何选择呢？既然能区分的工具这么多，那我们理所当然应该找一个最好的是不是？最佳答案应该是B，因为B与边数据的距离是最远的，之所以选择边距最远的线，是因为这样它的容错率更高，表现更稳定，也就是说当我们再次放入更多的点的时候，出错的概率更小
那么由此推导出，SVM的分类方法，首先考虑的是正确分类；其次考虑的优化数据到边界的距离。
接下来更麻烦的情景出现了，请看下图，这些点要怎么分？如果这是在一个二维平面上，这些应该用一条什么线来划分呢？

难道我们真的要在画一条无限曲折的线去划分吗?如果再怎样曲折还是无法区分又该怎么做呢？这就是线性不可分的情况，其实在现实生活中，大量的问题都线性不可分，而SVM正是处理这种线性不可分情况的好帮手。
处理这类问题的办法就是，将二维平面转化到一个三维空间，因为往往在低维空间下的非线性问题，转化到高维空间中，就变成了线性问题。比如说上面的图也许就变成了下方的情况

如上图所示，即三维样本数据被二维平面划分，在二维空间中的不可分问题也被转换成了三维线性可分问题，可以被支持向量机处理。基于这个思想，SVM采用核函数来实现低维空间到高维空间的映射，从而在一定程度上解决了低维空间线性不可分的问题。
下面我们简述一下关于核函数的定义，以利于进一步理解他的作用。
核函数：任意两个样本点在扩维后的空间的内积，如果等于这两个样本点在原来空间经过一个函数后的输出，那么这个函数就叫核函数。
作用：有了这个核函数，以后的高维内积都可以转化为低维的函数运算了，这里也就是只需要计算低维的内积，然后再平方。明显问题得到解决且复杂度极大降低。总而言之，核函数它本质上隐含了从低维到高维的映射，从而避免直接计算高维的内积。
常用的核函数有如下一些：例如线性核函数、多项式核函数、径向基核函数（RBF）、高斯核函数、拉普拉斯核函数、sigmoid核函数等等。
简单的理解了SVM的原理，我们再来了解一下模型的训练过程。
被所有的样本和其对应的分类标记交给算法进行训练。
如果发现线性可分，那就直接找出超平面。
如果发现现行不可分，那就映射到n+1维的空间，找出超平面。
最后得到超平面的表达式，也就是分类函数。
接下来我们来看看SVM是怎么应用于检测DGA的

首先加载数据集，数据集中包括从alexa获取的top1000的域名，这些都是正常url数据，以及从360 netlab（https://data.netlab.360.com/dga/）获取的1500条dga域名数据
统一放在了train-data.txt
可以分别使用head和tail命令来看一下

这里的0和1是我们打的标签，表示对应的域名为正常域名或者为dga域名
有了数据，接下来就是进行要找出能够区分这两种的域名的特征。
我们首先想到的就是信息熵（entropy）
信息熵做密码学或者做通信工程的同学应该都清楚，信息论之父 C. E. Shannon 在 1948 年发表的论文“通信的数学理论（ A Mathematical Theory of Communication ）”中指出，任何信息都存在冗余，冗余大小与信息中每个符号（数字、字母或单词）的出现概率或者说不确定性有关。Shannon 借鉴了热力学的概念，把信息中排除了冗余后的平均信息量称为“信息熵”，并给出了计算信息熵的数学表达式

其中，x表示随机变量，与之相对应的是所有可能输出的集合，定义为符号集,随机变量的输出用x表示。P(x)表示输出概率函数。变量的不确定性越大，熵也就越大，把它搞清楚所需要的信息量也就越大.
简单理解就是，对于一个随机字符串，信息熵就代表着字符串中字母出现以及分布的混乱程度。举个例子，对于字符串1：aaaaabbbbb,和字符串2：bhbvsdfhuye;两个字符串长度相同，但是字符串1更有规律，不确定性小，所以信息量小，信息熵也小。
我们在判断DGA时，用的第一个特征就是通过熵来判断域名的混乱程度。代码实现如下

我们可以预见，dga域名的组成更加随机、混乱，所以其熵会更大，我们可以使用下面几行代码绘图，来看看是否如此
x轴是label，y轴是熵的大小

测试如下，运行

得到下图

从图中可以看到和我们推测的是一致的；
好的，这个特征时可以用于区分正常域名和dga域名的，我们继续看看还有什么特征

我们知道，根据常规来说一个正常的网站一定会希望他的网站域名是读起来朗朗上口并且好记的组成，这种情况下，英语中元音字母的比例会比较高，而dga域名由于是由dga根据时间等因素随机生成的，所以dga域名中元音字母的比例相对来说不会高。我们使用下面的代码获得该比例

然后使用下面的代码绘图，x轴为label，y轴为比例

运行

得到下图

和我们分析的是一样的，所以这个特征也可以用于进行区分正常域名和恶意域名
我们注意到大部分dga域名的根域名不会是常见的，比如com,cn这种，一来这种域名注册费用比较贵，而来大部分是需要审核的，所以我们可以考虑通过根域名来进行区分。
使用下面的代码

这里我们假设根域名不是上图所示的cn,com等就是可疑的，给其打标签1，否则打标签0
接下来来同样进行绘图来看看，使用下图的代码

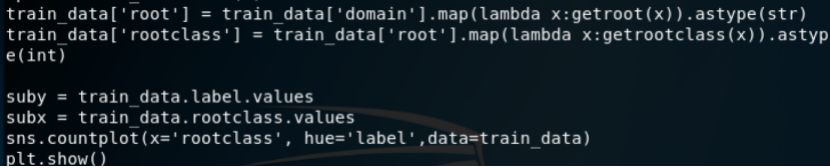
这里x轴为rootclass的label,0和1分别表示的是常见顶级域和非常见顶级域；y轴为计数
运行后得到下图

左上角的标注告诉我们蓝色代表数据集自身label为0，黄色代表数据集自身label为1
我们来解释一下这幅图
先看左边的两个rootclass为0 ，我们看出蓝色的比例更高；换句话来说，在根域名为常见顶级域名的情况下，该域名更大比例为正常域名
再看左边的两个rootclass为1,我们看出黄色的比例更高；换句话说，在根域名为不常见的顶级域名的情况下，该域名更大比例为dga域名
那么从图中的结果可以看出，这也可以作为一个特征
我们看看还有没有其他特征？比如域名的长度？
我们来简单实验下
使用下面的代码获取域名长度

然后绘图，x轴为域名长度，y轴为计数

运行后得到下面的图片

同样，蓝色代表正常域名，黄色代表dga域名，我们注意到，dga域名的长度比较集中，集中在7到16；而正常域名虽然在7到16比较集中，但是总体而言，每种长度都是有的，总体接近正态分布。
所以这也可以作为一个特征。
接下来就是要进行归一化，把数据变成(０，１)或者（1,1）之间的小数。主要是为了数据处理方便提出来的，把数据映射到一定范围之内处理，更加便捷快速。比如对于域名长度和熵值就需要归一化处理，代码如下

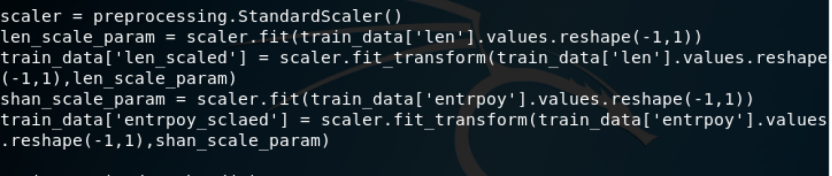
接着就是进行将这四个特征提取出来，使用shuffle()将数据集打乱顺序，避免相同label的数据都堆积在一起,然后使用as_matrix()转换为矩阵表示形式

然后切分训练集和测试集

选择SVM，核函数选择rbf，然后通过fit进行训练

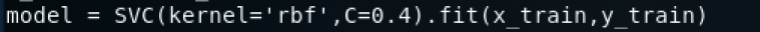
通过cross_val_score重复5次进行交叉验证

测试结果如下

进行5次得到的结果差异较大，甚至有准确率达到100%的情况，这是因为处于实验室机器性能的考虑，我们的样本数据集很小，导致效果不佳。

参考：
1.https://scikit-learn.org/stable/modules/model_evaluation.html#scoring-parameter
2.https://www.jianshu.com/p/95a8f035c86c
3.https://data.netlab.360.com/dga/
4.https://github.com/0FuzzingQ/dga_check
5.https://www.leiphone.com/news/201902/hJT3qqH1k4nbEKvP.html
6.https://zhuanlan.zhihu.com/p/31886934
7.https://blog.csdn.net/am290333566/article/details/81187124