- 1代码随想录算法训练营day41| 416. 分割等和子集
- 2基于python的opencv入门到精通(一)_python opencn
- 3英伟达H100算力出租,Punkhash探索AI无限,GB200/H800算力租赁解决方案GPU算力租赁成本揭秘史上最贵芯片Nvidia H100是什么?_英伟达h100租金
- 4MySql开启安全审计(audit审计插件)_mysql5.8审计插件
- 5IOS开发之CollectionView_ios开发 collectionview
- 6Ubuntu 22.04从零开始的SSH生涯(自用)_uabntu22.04 ssh
- 7pycharm配置copilot_pycharm设置copilot步骤
- 8web端实现rtsp实时推流视频播放可行性方案_rtsp webrtc方案--基于webrtc-streamer窗口分割
- 9Flink1.14 SplitEnumerator概念入门讲解与源码解析 (二)
- 10jbod模式和直通模式区别_华阳信通浅谈新零售模式与传统零售的区别
Retinex算法的C++/opencv实现_c++给定如下所示的低光图像(图3),对齐进行retinex修复,输出得到的反射图。注意:同
赞
踩
最近在做图像增强方面的算法,在参考了一些博客,论文和源代码后 ,自己整理了Retinex相关算法的opencv实现,在这里贴出来供大家参考,有不当的地方欢迎大家指出!
一.Retinex算法原理
基础理论:物体的颜色是由物体对长波(红色),中波(绿色),短波(蓝色)光线的反射能力来决定的,而不是由反射光强度的绝对值来决定的;物体的颜色不受光照非均匀性的影响,具有一致性,即Retinex算法是基于物体的颜色恒常性来实现的。
Retinex算法可以在图像的动态颜色范围压缩,边缘增强和颜色恒常三个方面达到平衡,在图像除雾方面有着较好的效果(对正常图像的增强效果不明显)。
二.SSR(Single Scale Retinex)
根据Retinex算法的基础理论,我们可以得到以下数学表达式:
S(x,y)=R(x,y)*L(x,y) (2-1)
图示如下:
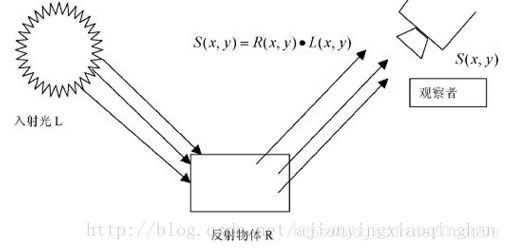
其中R(x,y)表示物体的反射性质,即图像的内在属性,应该最大程度的保留;L(x,y)表示入射光图像,决定了图像像素能够达到的动态范围,应该尽量去除;S(x,y)为人眼观察到或者相机接收到的图像。
对公式2-1的等式两边取对数,得到:
r(x,y)=Log[R(x,y)] = Log[S(x,y)]-Log[L(x,y)] (2-2)
算法的关键在于如何得到图像的入射光图像L(x,y),其中比较经典且效果较好的方法是通过对相机接收的图像S(x,y)做高斯模糊来估计L(x,y)。
算法的具体步骤如下:
(1)输入高斯模糊的高斯环绕尺度C(即二维高斯函数的标准差);
(2)根据C对原始图像数据S(x,y)做高斯模糊得到L(x,y);
(3)根据公式2-2对S(x,y)和L(x,y)分别取对数并作差得到r(x,y);
(4)将r(x,y)的像素值量化到0到255的范围内得到R(x,y),R(x,y)即我们想得到的增强图像。量化的公式如下:
R(x,y) = ( Value - Min ) / (Max - Min) * (255-0) (2-3)
算法的源代码如下:
void ssr(Mat src, Mat& dst, double sigma) { Mat src_log,gauss,gauss_log,dst_log; src_log= Mat(src.size(), CV_32FC3); gauss_log= Mat(src.size(), CV_32FC3); dst_log = Mat(src.size(), CV_32FC3); dst = Mat(src.size(), CV_32FC3); int height = dst_log.rows; int width = dst_log.cols; int ksize = (int)(sigma * 3/2); ksize = ksize * 2 + 1; //求Log(S(x,y) for (int i = 0;i < height;i++) { for (int j = 0;j < width;j++) { for (int k = 0;k < 3;k++) { float value = src.at<Vec3b>(i, j)[k]; if (value <= 0.01) value = 0.01; src_log.at<Vec3f>(i, j)[k] = log10(value); } } } GaussianBlur(src, gauss, Size(ksize,ksize),sigma,sigma,4); //求Log(L(x,y)) for (int i = 0;i < height;i++) { for (int j = 0;j < width;j++) { for (int k = 0;k < 3;k++) { float value = gauss.at<Vec3b>(i, j)[k]; if (value <= 0.01) value = 0.01; gauss_log.at<Vec3f>(i, j)[k] = log10(value); } } } //求Log(S(x,y))-Log(L(x,y)) for (int i = 0;i < height;i++) { for (int j = 0;j < width;j++) { for (int k = 0;k < 3;k++) { float value1 = src_log.at<Vec3f>(i, j)[k]; float value2 = gauss_log.at<Vec3f>(i, j)[k]; dst_log.at<Vec3f>(i, j)[k] = value1-value2; } } } float min[3] = { dst_log.at<Vec3f>(0, 0)[0], dst_log.at<Vec3f>(0, 0)[1],dst_log.at<Vec3f>(0, 0)[2] }; float max[3] = { dst_log.at<Vec3f>(0, 0)[0], dst_log.at<Vec3f>(0, 0)[1],dst_log.at<Vec3f>(0, 0)[2] }; //求R/G/B三通道的min,max for (int i = 0;i < height;i++) { for (int j = 0;j < width;j++) { for (int k = 0;k < 3;k++) { float value = dst_log.at<Vec3f>(i, j)[k]; if (value > max[k]) max[k] = value; if (value < min[k]) min[k] = value; } } } //量化处理 cout << min[0] << " " << min[1] << " " << min[2] << endl; cout << max[0] << " " << max[1] << " " << max[2] << endl; for (int i = 0;i < height;i++) { for (int j = 0;j < width;j++) { for (int k = 0;k < 3;k++) { float value = dst_log.at<Vec3f>(i, j)[k]; dst.at<Vec3f>(i, j)[k] = (saturate_cast<float>(255 * (value - min[k]) / (max[k] - min[k]))); } } } dst.convertTo(dst, CV_8UC3); return; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
效果图如下:
原图:

SSR(C=300):

原图:

SSR(C=300):

三.MSR(Multi Scale Retinex)
MSR是在SSR算法的基础上提出的,用不同的尺度C来估计L(x,y)。数学表达如下:
r(x,y)=∑k Wk*{logS(x,y)−log[Fk(x,y)⋅S(x,y)]} (3-1)
为了兼有SSR高,中,低三个尺度的优点的考虑,K通常取3,且有W1=W2=W3=1/3.
算法步骤:
(1)输入权值矩阵Wk和K个高斯环绕尺度;
(2)根据公式3-1得到r(x,y);
(3)对r(x,y)做量化处理得到增强图像R(x,y).
算法的源代码如下:
void msr(Mat src, Mat& dst, vector<float>weight, vector<float>sigmas) { Mat src_log, gauss, gauss_log, dst_log; src_log = Mat(src.size(), CV_32FC3); gauss_log = Mat(src.size(), CV_32FC3); dst_log = Mat::zeros(src.size(), CV_32FC3); dst = Mat::zeros(src.size(), CV_32FC3); int height = dst_log.rows; int width = dst_log.cols; //求Log(S(x,y) for (int i = 0;i < height;i++) { for (int j = 0;j < width;j++) { for (int k = 0;k < 3;k++) { float value = src.at<Vec3b>(i, j)[k]; if (value < 0.01) value = 0.01; src_log.at<Vec3f>(i, j)[k] = log10(value); } } } int scale = weight.size(); for (int t = 0;t < scale;t++) { int ksize = (int)(sigmas[t] * 3 / 2); ksize = ksize * 2 + 1; GaussianBlur(src, gauss, Size(ksize, ksize), sigmas[t], sigmas[t], 4); //求Log(L(x,y)) for (int i = 0;i < height;i++) { for (int j = 0;j < width;j++) { for (int k = 0;k < 3;k++) { float value = gauss.at<Vec3b>(i, j)[k]; if (value < 0.01) value = 0.01; gauss_log.at<Vec3f>(i, j)[k] = log10(value); } } } //求Log(S(x,y))-Log(L(x,y)) for (int i = 0;i < height;i++) { for (int j = 0;j < width;j++) { for (int k = 0;k < 3;k++) { float value1 = src_log.at<Vec3f>(i, j)[k]; float value2 = gauss_log.at<Vec3f>(i, j)[k]; dst_log.at<Vec3f>(i, j)[k] +=weight[t] * (value1 - value2); } } } } float min[3] = { dst_log.at<Vec3f>(0, 0)[0], dst_log.at<Vec3f>(0, 0)[1],dst_log.at<Vec3f>(0, 0)[2] }; float max[3] = { dst_log.at<Vec3f>(0, 0)[0], dst_log.at<Vec3f>(0, 0)[1],dst_log.at<Vec3f>(0, 0)[2] }; //求R/G/B三通道的min,max for (int i = 0;i < height;i++) { for (int j = 0;j < width;j++) { for (int k = 0;k < 3;k++) { float value = dst_log.at<Vec3f>(i, j)[k]; if (value > max[k]) max[k] = value; if (value < min[k]) min[k] = value; } } } //量化处理 for (int i = 0;i < height;i++) { for (int j = 0;j < width;j++) { for (int k = 0;k < 3;k++) { float value = dst_log.at<Vec3f>(i, j)[k]; dst.at<Vec3f>(i, j)[k] =saturate_cast<float> (255 * (value - min[k]) / (max[k] - min[k])); } } } dst.convertTo(dst, CV_8UC3); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
算法的效果图如下:
原图:

MSR(C1=40,C2=100,C3=300):

原图:

MSR(C1=40,C2=100,C3=300):

四.MSRCR(带颜色恢复的MSR)
由SSR和MSR算法的效果图我们可以看到一般的Retinex算法在图像去雾时可能会导致图像失真。一般的Retinex算法处理图像时,都会假设初始图像灰度值是缓慢变化的,即图像是平滑的,在实际情况下,Retinex算法在亮度差异大的区域会产生光晕。
为了解决上述的图像颜色失真的情况,有人提出了一种带有颜色恢复的MSR算法。MSRCR算法在MSR算法的基础上,加入了色彩恢复因子来调节由于图像局部区域对比度增强导致的颜色失真。
算法核心如下:

算法源代码如下:
void scr(Mat &src, float low_clip, float high_clip) { int height = src.rows; int width = src.cols; int total = height*width; int u[3][256];//统计每个通道每个像素值出现的次数 memset(u, 0, sizeof(u)); for (int i = 0;i < height;i++) { for (int j = 0;j < width;j++) { for (int k = 0;k < 3;k++) { int v = src.at<Vec3b>(i, j)[k]; u[k][v]++; } } } for (int i = 0; i < 3; i++) { for (int j = 1;j < 256;j++) { u[i][j] = u[i][j - 1] + u[i][j]; } } int low_val[3], high_val[3]; float low_rate = 0, high_rate = 0; for (int i = 0; i < 3; i++) { for (int j = 0;j < 256;j++) { float rate = u[i][j] / total; if (rate< low_clip&&rate>low_rate) { low_val[i] = j; low_rate = rate; } if (rate < high_clip&&rate>high_rate) { high_val[i] = j; high_rate = rate; } } } for (int i = 0;i < height;i++) { for (int j = 0;j < width;j++) { for (int k = 0;k < 3;k++) { int value = src.at<Vec3b>(i, j)[k]; src.at<Vec3b>(i, j)[k] = max(min(value, high_val[k]), low_val[k]); } } } } void colorRestoration(Mat src, Mat& dst, float alpha, float beta) { dst = Mat(src.size(), CV_32FC3); for (int i = 0; i < src.rows; i++) { for (int j = 0;j < src.cols;j++) { float sum = 0; for (int t = 0;t < src.channels();t++) sum += src.at<Vec3b>(i, j)[t]; for (int k=0;k<3;k++) { dst.at<Vec3f>(i, j)[k] = beta*(log10(alpha*src.at<Vec3b>(i, j)[k]) - log10(sum)); } } } } void msrcr(Mat src, Mat& dst, vector<float>weight, vector<float>sigmas, float alpha, float beta, float low_clip, float high_clip) { Mat src_log, gauss, gauss_log, dst_log,dst_ci; src_log = Mat(src.size(), CV_32FC3); gauss_log = Mat(src.size(), CV_32FC3); dst_log = Mat::zeros(src.size(), CV_32FC3); dst_ci = Mat(src.size(), CV_32FC3); dst = Mat::zeros(src.size(), CV_32FC3); int height = dst_log.rows; int width = dst_log.cols; //求Log(S(x,y) for (int i = 0;i < height;i++) { for (int j = 0;j < width;j++) { for (int k = 0;k < 3;k++) { float value = src.at<Vec3b>(i, j)[k]; if (value < 0.01) value = 0.01; src_log.at<Vec3f>(i, j)[k] = log10(value); } } } int scale = weight.size(); for (int t = 0;t < scale;t++) { int ksize = (int)(sigmas[t] * 3 / 2); ksize = ksize * 2 + 1; GaussianBlur(src, gauss, Size(ksize, ksize), sigmas[t], sigmas[t], 4); //求Log(L(x,y)) for (int i = 0;i < height;i++) { for (int j = 0;j < width;j++) { for (int k = 0;k < 3;k++) { float value = gauss.at<Vec3b>(i, j)[k]; if (value < 0.01) value = 0.01; gauss_log.at<Vec3f>(i, j)[k] = log10(value); } } } //求Log(S(x,y))-Log(L(x,y)) for (int i = 0;i < height;i++) { for (int j = 0;j < width;j++) { for (int k = 0;k < 3;k++) { float value1 = src_log.at<Vec3f>(i, j)[k]; float value2 = gauss_log.at<Vec3f>(i, j)[k]; dst_log.at<Vec3f>(i, j)[k] += weight[t] * (value1 - value2); } } } } //求色彩恢复因子Ci colorRestoration(src, dst_ci, alpha, beta); for (int i = 0;i < height;i++) { for (int j = 0;j < width;j++) { for (int k = 0;k < 3;k++) { float v1 = dst_log.at<Vec3f>(i, j)[k]; float v2 = dst_ci.at<Vec3f>(i, j)[k]; dst_log.at<Vec3f>(i, j)[k] = v1*v2 ; } } } float min[3] = { dst_log.at<Vec3f>(0, 0)[0], dst_log.at<Vec3f>(0, 0)[1],dst_log.at<Vec3f>(0, 0)[2] }; float max[3] = { dst_log.at<Vec3f>(0, 0)[0], dst_log.at<Vec3f>(0, 0)[1],dst_log.at<Vec3f>(0, 0)[2] }; //求R/G/B三通道的min,max for (int i = 0;i < height;i++) { for (int j = 0;j < width;j++) { for (int k = 0;k < 3;k++) { float value = dst_log.at<Vec3f>(i, j)[k]; if (value > max[k]) max[k] = value; if (value < min[k]) min[k] = value; } } } //量化处理 for (int i = 0;i < height;i++) { for (int j = 0;j < width;j++) { for (int k = 0;k < 3;k++) { float value = dst_log.at<Vec3f>(i, j)[k]; dst.at<Vec3f>(i, j)[k] = saturate_cast<float> (255 * (value - min[k]) / (max[k] - min[k])); } } } dst.convertTo(dst, CV_8UC3); scr(dst, low_clip, high_clip); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
上面的算法有着很多的经验参数,不利于手动实现,有人提出了一种基于GIMP的MSR算法,用参数Dynamic来控制图像的动态范围实现去除图像的色偏问题(一般取值2或3效果比较好)。这种算法的效果很好,能够一定程度解决颜色失真的问题。
算法的简要描述如下:
1.计算出 log[R(x,y)]中R/G/B各通道数据的均值Mean和均方差Var(注意是均方差)。
2.类似下述公式计算各通道的Min和Max值。
Min = Mean - Dynamic * Var;
Max = Mean + Dynamic * Var;
3.对Log[R(x,y)]的每一个值Value,进行线性映射:
R(x,y) = ( Value - Min ) / (Max - Min) * (255 - 0)
同时要注意增加一个溢出判断,即:
if (R(x, y) > 255) R(x,y) = 255;
else if (R(x,y) < 0) R(x,y) = 0;
算法的源码如下:
void msrcr_GIMP(Mat src, Mat& dst, vector<float>weight, vector<float>sigmas, int Dynamic) { Mat src_log, gauss, gauss_log, dst_log; src_log = Mat(src.size(), CV_32FC3); gauss_log = Mat(src.size(), CV_32FC3); dst_log = Mat(src.size(), CV_32FC3); dst = Mat(src.size(), CV_32FC3); float min[3] = { 0 }; float max[3] = { 0 }; float mean[3] = { 0 }; float var[3] = { 0 }; int height = dst_log.rows; int width = dst_log.cols; //求Log(S(x,y) for (int i = 0;i < height;i++) { for (int j = 0;j < width;j++) { for (int k = 0;k < 3;k++) { float value = src.at<Vec3b>(i, j)[k]; if (value < 0.01) value = 0.01; src_log.at<Vec3f>(i, j)[k] = log10(value); } } } int scale = weight.size(); for (int t = 0;t < scale;t++) { int ksize = (int)(sigmas[t] * 3 / 2); ksize = ksize * 2 + 1; GaussianBlur(src, gauss, Size(ksize, ksize), sigmas[t], sigmas[t], 4); //求Log(L(x,y)) for (int i = 0;i < height;i++) { for (int j = 0;j < width;j++) { for (int k = 0;k < 3;k++) { float value = gauss.at<Vec3b>(i, j)[k]; if (value < 0.01) value = 0.01; gauss_log.at<Vec3f>(i, j)[k] = log10(value); } } } //求Log(S(x,y))-Log(L(x,y)) for (int i = 0;i < height;i++) { for (int j = 0;j < width;j++) { for (int k = 0;k < 3;k++) { float value1 = src_log.at<Vec3f>(i, j)[k]; float value2 = gauss_log.at<Vec3f>(i, j)[k]; dst_log.at<Vec3f>(i, j)[k] += weight[t] * (value1 - value2); } } } } //求R/G/B各通道的均值mean和均方差var float sum[3] = {0}; for (int i = 0;i < height;i++) { for (int j = 0;j < width;j++) { for (int k = 0;k < 3;k++) { float value = dst_log.at<Vec3f>(i, j)[k]; sum[k] += value; } } } for (int i = 0; i < 3; i++) { mean[i] = sum[i] / (height*width); } for (int i = 0;i < height;i++) { for (int j = 0;j < width;j++) { for (int k = 0;k < 3;k++) { float value = dst_log.at<Vec3f>(i, j)[k]; var[k] += (value - mean[k])*(value - mean[k]); } } } for (int i = 0; i < 3; i++) { var[i] = sqrt(var[i] / (height*width)); } //计算R/G/B各通道的Min,Max for (int i = 0; i < 3; i++) { min[i] = mean[i] - Dynamic*var[i]; max[i] = mean[i] + Dynamic*var[i]; } //量化处理 for (int i = 0;i < height;i++) { for (int j = 0;j < width;j++) { for (int k = 0;k < 3;k++) { float value = dst_log.at<Vec3f>(i, j)[k]; dst.at<Vec3f>(i, j)[k] = saturate_cast<float>(255 * (value - min[k]) / (max[k] - min[k])); } } } dst.convertTo(dst, CV_8UC3); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
算法的效果图如下:
MSR(C1=40,C2=100,C3=300):

MSRCR_GIMP(C1=40,C2=100,C3=300,Dynamic=2):

原图:

MSRCR_GIMP(C1=40,C2=100,C3=300,Dynamic=2):

以上就是我的Retinex算法的总结过程,算法本人已经实现过,效果图也贴出来供大家参考,有不当的地方欢迎大家指出来,楼主会及时修正,最后希望我的总结能够帮到大家!



