- 1传输门、D 锁存器、D触发器、建立时间与保持时间_传输门dff
- 2【SpringBoot】SpringBoot拦截器_springboot 配置拦截器
- 3minicom/picocom/cutecom/putty 安装与使用教程_安装picocom 串口模拟软件
- 4vue3 van-list van-pull-refresh实现上拉加载,下拉刷新
- 5知攻善防靶机应急响应web3
- 6Java:缓存行和伪共享
- 7【巨人的肩膀上制造世界】——7——Unity3D实用插件之Dynamic Fog Mist,快速简洁的制作高质量的动态迷雾效果_unity3d slg迷雾
- 8防火墙之流量管理
- 9HBASE的伪分布安装(简单)_hbase伪分布模式
- 10NEO4J的安装配置及使用总结_neo4j安装教程
十大经典排序算法详解(三)-堆排序,计数排序,桶排序,基数排序_堆排序,计数排序,基数排序
赞
踩
养成习惯,先赞后看!!!
你的点赞与关注真的对我非常有帮助.如果可以的话,动动手指,一键三连吧!!!
十大经典排序算法-堆排序,计数排序,桶排序,基数排序
前言
这是十大经典排序算法详解的最后一篇了.
还没有看多之前两篇文章的小伙伴可以先去看看之前的两篇文章:
十大经典排序算法详解(一)冒泡排序,选择排序,插入排序
十大经典排序算法详解(二)希尔排序,归并排序,快速排序
这一篇文章真的耗费了我巨大的时间和精力,由于 堆排序是基于二叉树 的,所以写的篇幅比较大并且由于是关于树的,所以画图动态演示的工程量就进一步增加,其次就是因为计数排序,桶排序以及基数排序并不是基于比较的,所以算法的思想讲解相对于之前的基于比较的算法而言会稍微难一点.
其次就是这次的调试过程也比之前多了很多需要注意的地方,这些我都会在下面的代码中通过注释的方式提醒大家.
最后如果大家觉得我的文章写得还可以或者觉得文章对你有帮助的话,可以选择关注我的公众号:萌萌哒的瓤瓤,或者你也可以帮忙给文章来个一键三连吧.你的支持对我真的很有用.

1-堆排序
算法思想:
在介绍算法之前我们首先需要了解一下下面这些概念:什么是二叉树,什么是完全二叉树,什么是大根堆,什么是小根堆.
二叉树
学过数据结构的小伙伴肯定知道什么是二叉树,这部分主要是为那些可能还不太了解数据结构的小伙伴们说的.
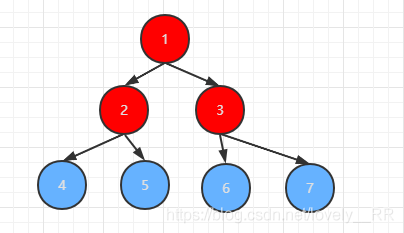
二叉树的定义就是每个结点至多能有两个子树,二叉树是一种最简单的树,下面我们举几个树的例子:

我们可以来哦稍微区分一下,很明显只有4号树并不是我们所说的二叉树,因为它的1号结点下有三棵子树,所以4号树并不是我们所说的二叉树.到这里,相信大家也已经基本了解二叉树得出概念了,那么接下来我们再来了解一下另一个概念完全二叉树.
完全二叉树
说到完全二叉树,就应该知道它首先应该满足二叉树的一些条件,就比如说每个节点至多只能有两个子树,那么除了这个条件以外,还需要什么条件才能称得上是完全二叉树呢.
官方是这样说的: 一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树。
但是很明显说的太官方了,我们肯定需要简化一下概念.其实说白了就是在二叉树的基础上,所有的节点顺序必须要按照下面这样的顺序进行排列,否则就不能说是完全二叉树
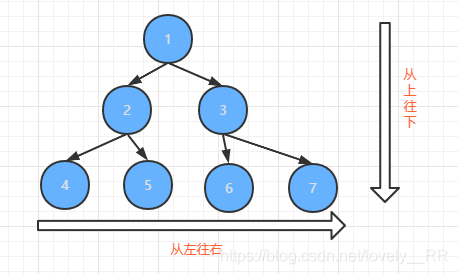
并且每次必须是已经放满2的幂数之后才能放到下一层,并且必须是从每层最左边的节点开始添加节点,并且必须是先添加左节点在添加右节点.否则就不能称为是完全二叉树,这里呢,我们举几个反例,大家就知道我说的是什么意思了:
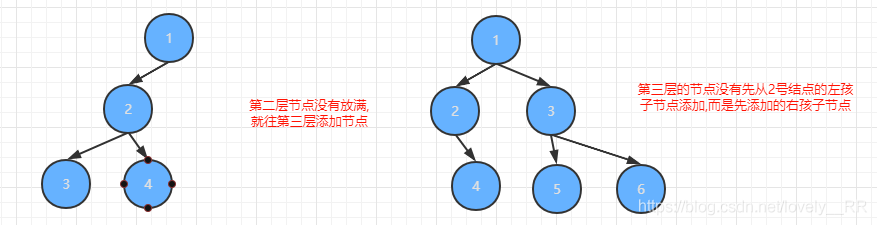
上面的这两棵树就是最明显的反例,看完这两棵树之后,相信大家就能更加了解什么是完全二叉树了.
大根堆
大根堆其实很容易理解,大根堆在完全二叉树的基础上就一条判定条件就是:每个根节点的值必须大于它的左孩子节点已经右孩子节点的值.满足这样条件的二叉树,我们就称这个二叉树是大根堆.当然了只要有一个节点不满足这样的情况,那么就不能称这是大根堆.
举个例子,下面这棵二叉树就是一个大根堆:
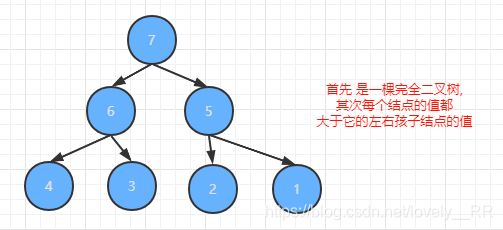
举完正确的例子之后,我们当然也需要来举几个反例来帮助我们更好的理解什么是大根堆:
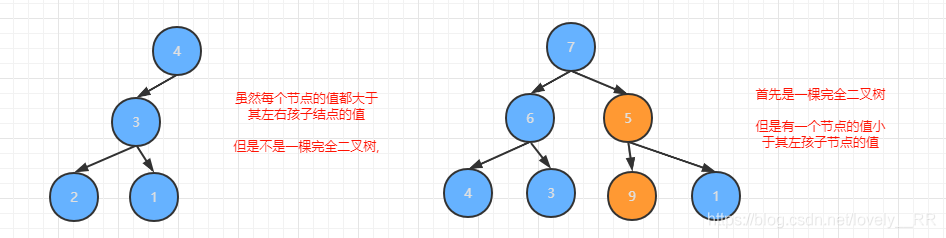
看完这两个反例之后相信大家就能更加理解什么是大根堆了.
小根堆
当然了,理解完什么是大根堆了之后,大家就能举一反三的了解什么叫做小根堆了.这里就不再给大家废话.
在了解完上面的这些概念之后,我们就可以来讲解什么是堆排序了.
堆排序的算法步骤其实很简单,总共就三步.
-
1.将数组重构成大根堆
-
2.将数组的
队头元素与队尾元素交换位置 -
3.对去除了队尾元素的数组进行重构,再次重构成大根堆
之后重复上述2,3步骤,直到需要重构成大根堆的数组为空为止.
算法的步骤的确简洁明了,其实大家看了也应该已经懂了.
因为每次重构成大根堆之后,根据大根堆的特性,每个节点的值一定大于左右孩子节点的值,所以很明显大根堆的根节点就是二叉树中值最大的值同时也就是数组中最大的值.所以重构成大根堆之后交换数组队头与队尾元素的操作就是在将最大的元素进行定位.也就意味着这一轮结束之后,数组中已经确定了一个元素的最终位置了.
算法的思想就是这样,谁都能说的出来,但是呢,堆排序的难点就是在于我们如何将数组重构成我们大根堆.这个就是堆排序的难点.
那么接下来,我们就着重讲解一下重构大根堆的过程是怎么样的.
首先我们需要明白一点就是我们一开始构建二叉树的时候遵循的是这样的原则: 从上往下,从左往右 .但是到了将二叉树重构成大根堆的时候我们的原则就必须要反过来了:从下往上,从右往左.这个大家动动小脑瓜应该就能理解了.
显然我们每次对小子树进行重构成大根堆的操作时,最后都会使得最大的元素上移,对不对,既然大的元素是在上移的,那么很显然我们就应该从下往上开始构建.
既然我们已经知道重构的顺序是什么样的之后,我们就需要再明白一点,那就是我们应该对哪些元素进行重构的操作呢?上面我们已经说过了,大根堆的一个硬性条件就是每个节点必需要大于它的左右孩子节点,那么很显然如果节点本身没有孩子节点的话,就不需要进行重构了.所以我们需要进行重构的元素必定包含孩子节点.并且结合我们上面所说重构顺序基本就可以得出一个结论:重构的元素就是最后一个非叶子节点之前的所有节点,包括该节点本身.,就比方下面这张图中红色圈圈的元素.
之后我们只需要通过循环,依次进行下面的操作:
比较节点及其左右孩子节点,如果有孩子节点的值大于该节点,那么就交换两者的位置.
这里需要大家特别注意!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
这里需要大家特别注意!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
这里需要大家特别注意!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
交换两者的位置之后我们还需要进行一个步骤 重新校验
特别注意!!!特别注意!!!重复这个过程,直到最后一个元素为止.
到这里堆排序的基本思想也就已经基本讲解完毕了,接下来就是通过图来动态的演示一下堆排序的过程,这样能够让大家更好的理解堆排序:
这是第一轮堆排序:
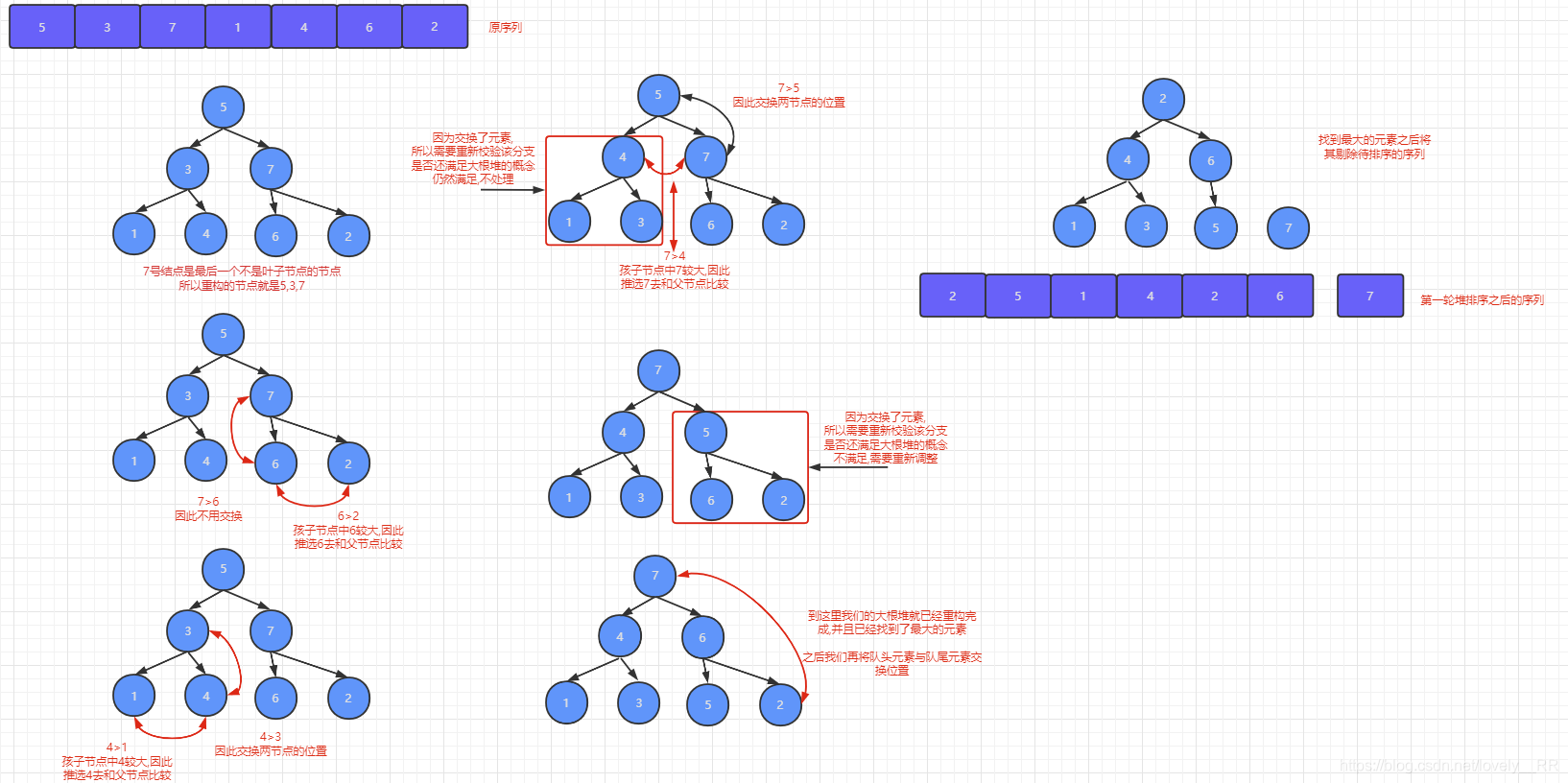 )
)
第二次堆排序:
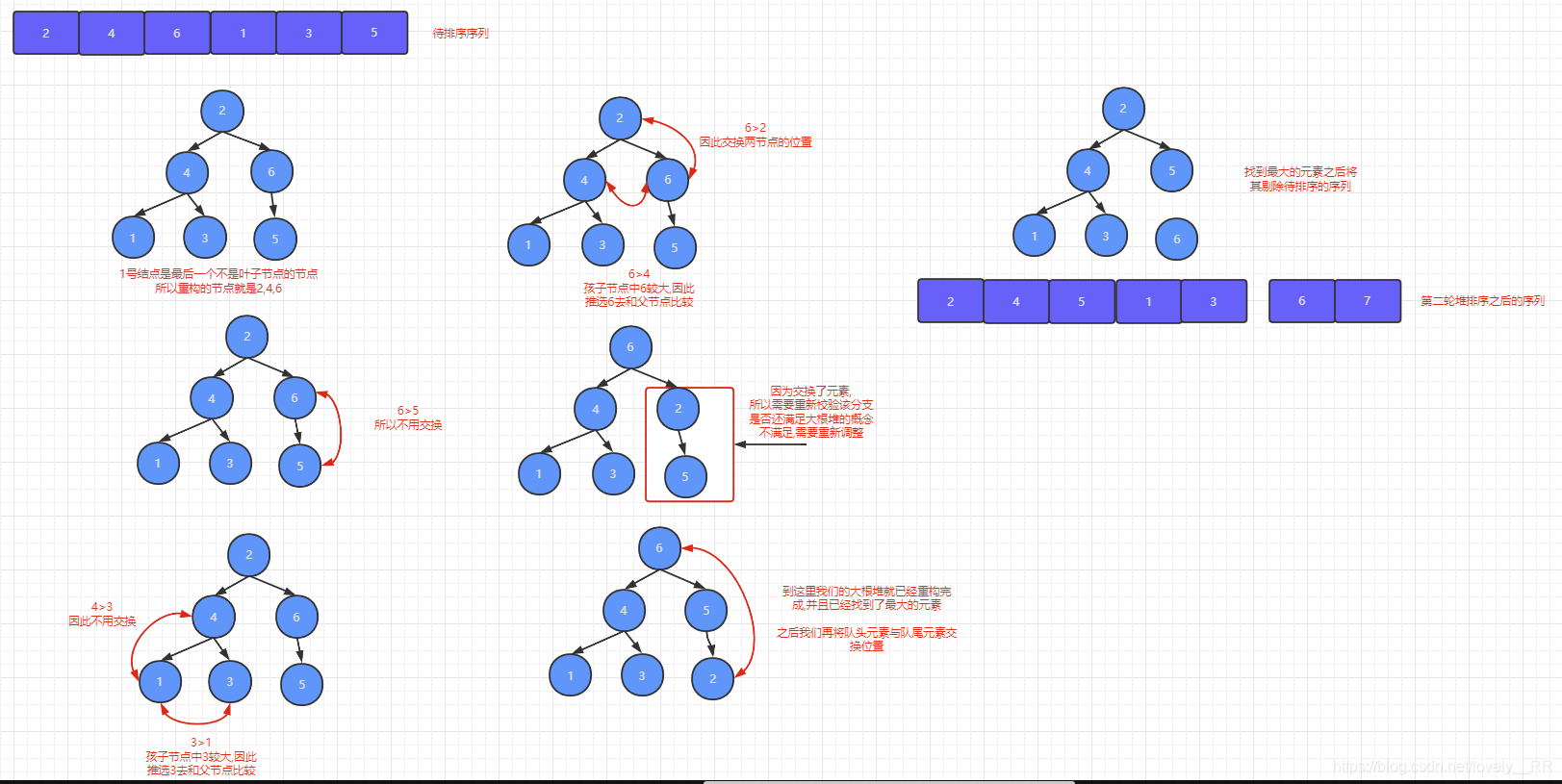 )
)
第三次堆排序:
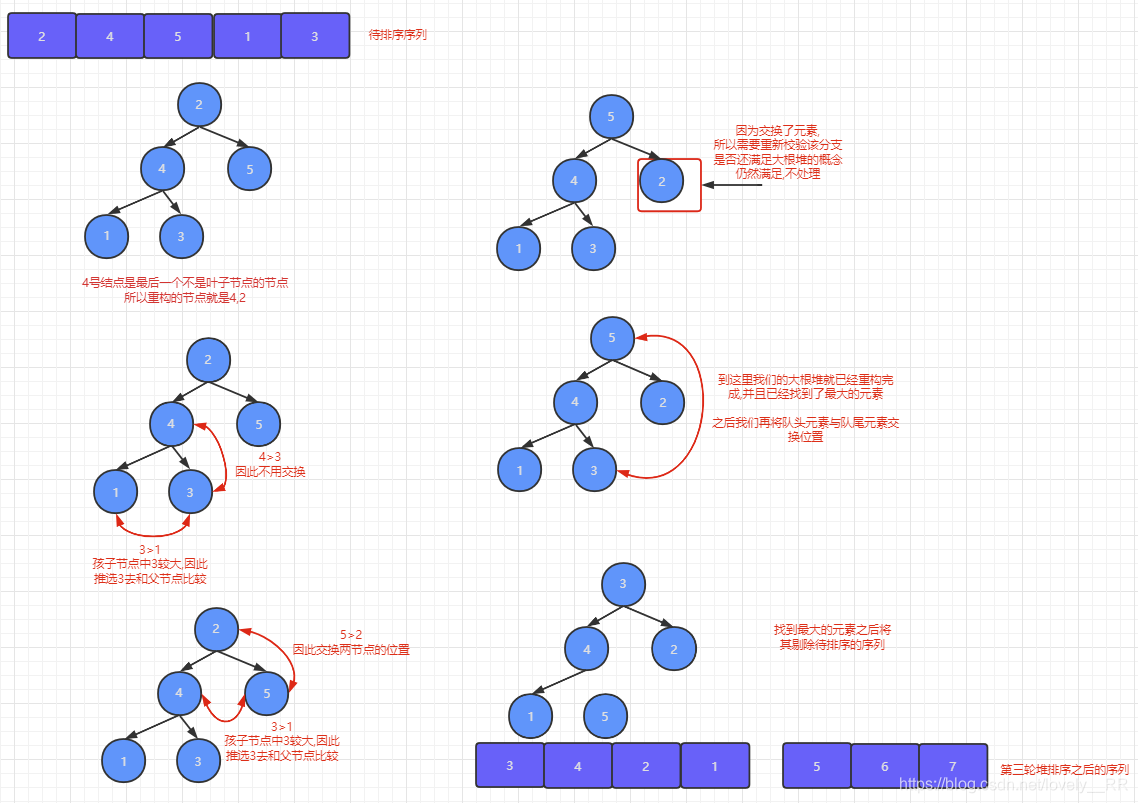 )
)
这里给大家模拟三次,大家应该就差不多懂这个流程了.主要是这图图画起来实在是太麻烦了.能力有限就只画这三次的了.在下面的代码里面,我还会着重讲重新校验的过程,大家如果这里还没理解的,也可以接着往下面看.
算法的基本思想大家应该基本上就能理解了.那么我们再来稍微聊聊堆排序的一些特点:
-
堆排序是
不稳定的,这个其实还是比较好理解的.因为我们在进行小分支的调整时时有序的,但是之后可能会出现小分支扩大到大分支进行重新的调整,那么这时候就有可能会出现元素的相对位置混乱的情况.这个混乱的过程其实有点像我们之前所说的
希尔排序,希尔排序也是小区间内的插入排序是有序的,但是一旦扩散到更大的区间进行二次的插入排序时就有可能造成相对位置混乱的情况.说的差不多了,那么我们接下来还是举一个例子来帮助大家更好的理解:
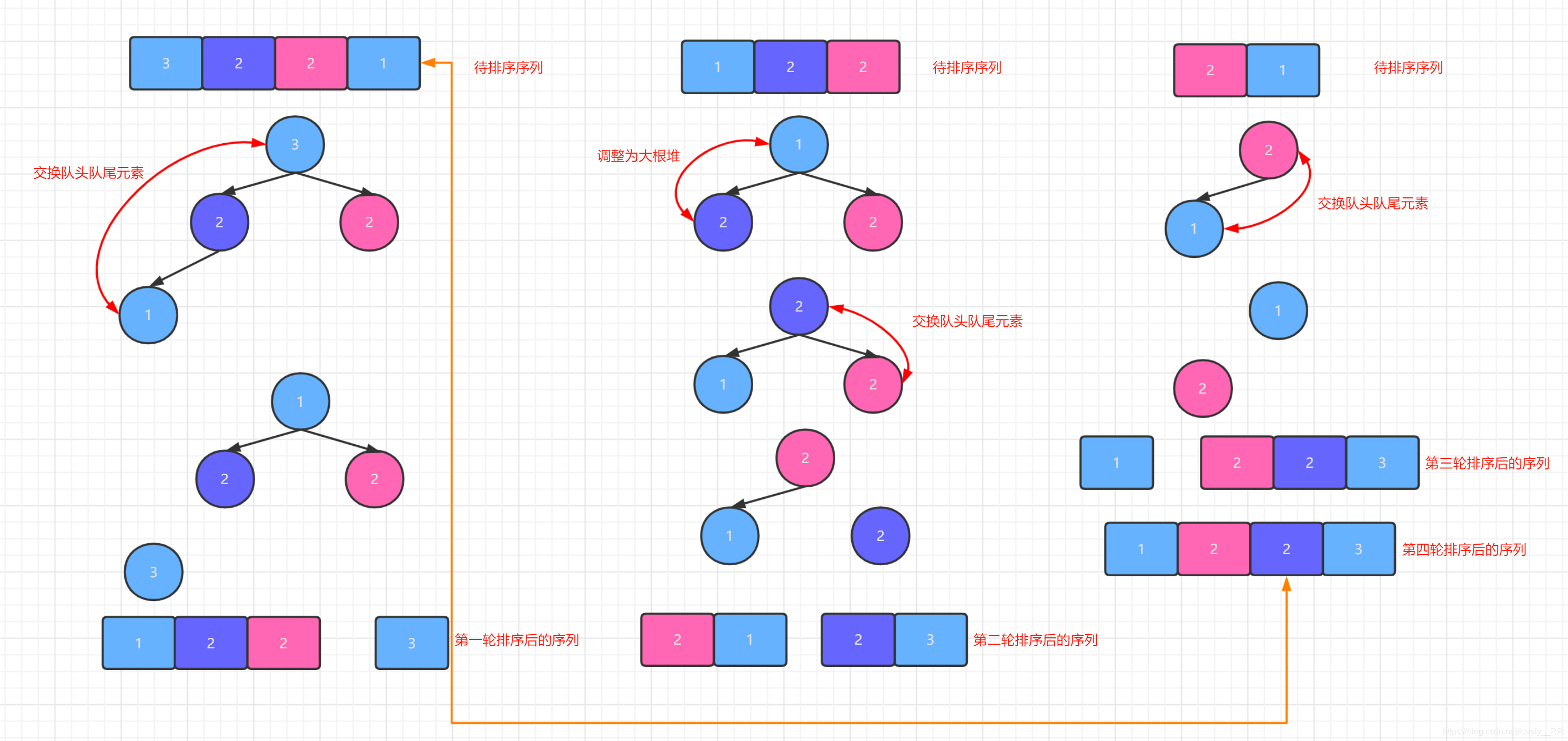
通过上面这张图,相信大家就能更好的理解堆排序为啥是不稳定的了. -
堆排序每轮排序都可以确定
一个元素的最终位置,这个大家看我上面的演示图也能看出来.
算法图解:

示例代码:
这是我写的第一版的代码:
//交换数组中的元素 public static void swap(int[]num ,int i,int j) { int temp=num[i]; num[i]=num[j]; num[j]=temp; } //将待排序的数组构建成大根堆 public static void buildbigheap(int []num,int end) { //从最后一个非叶子节点开始构建,依照从下往上,从右往左的顺序 for(int i=end/2;i>=0;i--) { int left=2*i+1; int right=2*i+2; int big=i; //判断小分支那个是大元素 if(left<end&&num[i]<num[left]) // swap(num, i, left); i=left; if(right<end&&num[i]<num[right]) // swap(num, i, right); i=right; swap(num, i, big); } } public static void main(String[] args) { int []num ={7,4,9,3,2,1,8,6,5,10}; long startTime=System.currentTimeMillis(); //第一次构建大根堆 buildbigheap(num, num.length); for(int j=num.length-1;j>0;j--) { //交换队头已经排序得到的最大元素与队尾元素 swap(num, 0, j); System.out.print("第"+(num.length-j)+"次排序: "); for(int k=0;k<num.length;k++) { System.out.print(num[k]+" "); } System.out.println(); //交换结束之后,大根堆已经内破坏,需要开始重新构建大根堆 buildbigheap(num,j); } long endTime=System.currentTimeMillis(); System.out.println("程序运行时间: "+(endTime-startTime)+"ms"); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
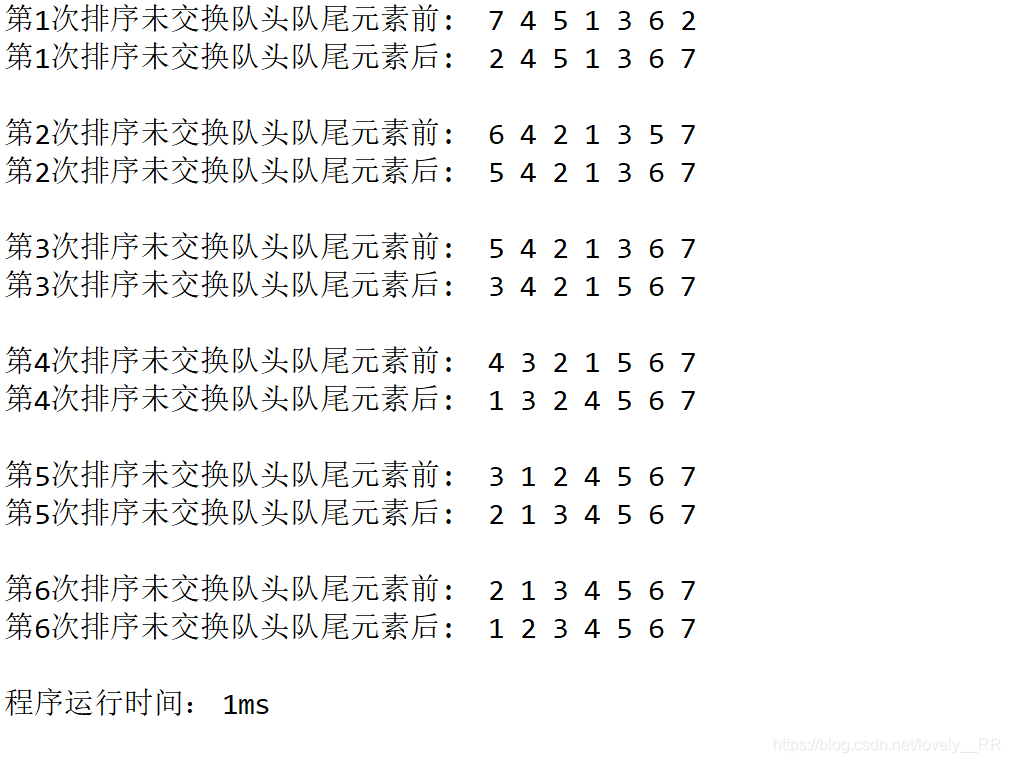
一开始我觉得我的代码是对的,并且运行出来的结果也和我预期的一样,但是当我自己画图以后画到这张图的时候我就知道算法还是有BUG的,这个BUG就是每次构建大根堆的时候:我们的确能够在每次构建大根堆的时候将最大的元素挑选出来,但是,我们在挑选出当前最大的元素之后,我们的大根堆真的还是大根堆吗,这里用上面画的图,我们就能看出来了:

很明显这个这一步我们的确已经将最大的元素挑选出来了,但是我们当前的已经不是大根堆了,所以我就在想我到底是哪一步做错了呢.之后我参考了网上的资料发现,该算法还有一个重点就是:如果我们发现根节点与孩子节点交换顺序之后,我们就需要重新检查交换之后的孩子节点以下的所有节点是否还满足大根堆的定义,因为可能我们交换后的孩子节点的值还是比他的孩子节点要小的.就比方上面那张图里我们所看到的.所以修改后的代码主要就是加上了重新校验的过程.
修改后的第二版代码:
//交换数组中的元素 public static void swap(int[]num ,int i,int j) { int temp=num[i]; num[i]=num[j]; num[j]=temp; } //将待排序的数组构建成大根堆 public static void buildbigheap(int []num,int end) { //从最后一个非叶子节点开始构建,依照从下往上,从右往左的顺序 for(int i=end/2;i>=0;i--) { adjustnode(i, end, num); } } //调整该节点及其以下的所有节点 public static void adjustnode(int i,int end,int []num) { int left=2*i+1; int right=2*i+2; int big=i; //判断小分支那个是大元素 if(left<end&&num[i]<num[left]) i=left; if(right<end&&num[i]<num[right]) i=right; if(i!=big) { //交换顺序之后需要继续校验 swap(num, i, big); //重新校验,防止出现交换之后根节点小于孩子节点的情况 adjustnode(i, end, num); } } public static void main(String[] args) { int []num ={5,3,7,1,4,6,2}; long startTime=System.currentTimeMillis(); //第一次构建大根堆 buildbigheap(num, num.length); for(int j=num.length-1;j>0;j--) { System.out.print("第"+(num.length-j)+"次排序前: "); for(int k=0;k<num.length;k++) { System.out.print(num[k]+" "); } //交换队头已经排序得到的最大元素与队尾元素 swap(num, 0, j); System.out.print("第"+(num.length-j)+"次排序后: "); for(int k=0;k<num.length;k++) { System.out.print(num[k]+" "); } System.out.println(); //交换结束之后,大根堆已经被破坏,需要开始重新构建大根堆 buildbigheap(num,j); } long endTime=System.currentTimeMillis(); System.out.println("程序运行时间: "+(endTime-startTime)+"ms"); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
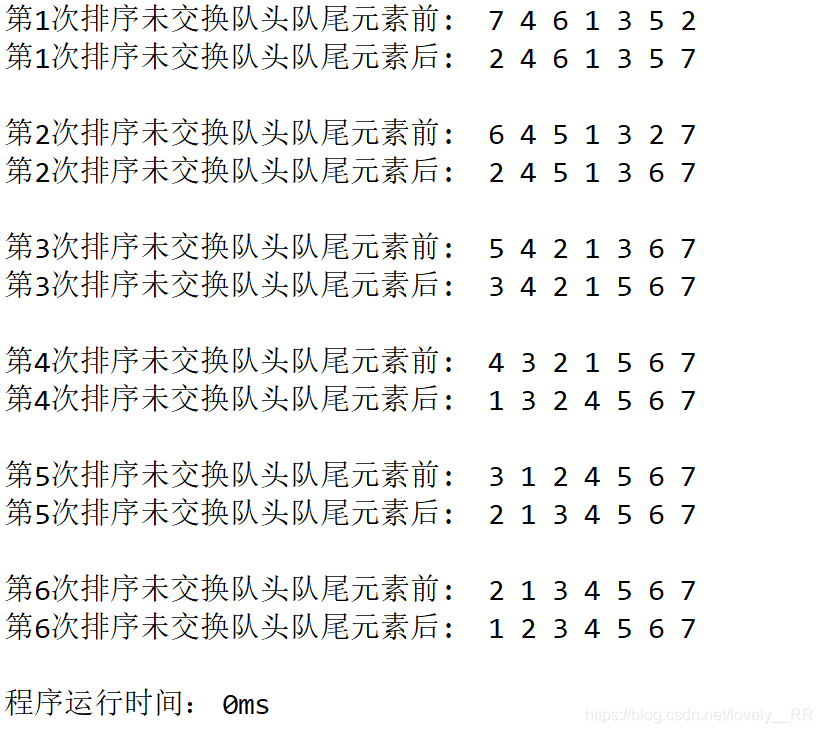
这里我们将这两个排序结果对比一下,大家就更加能了解重新校验步骤的重要性了.
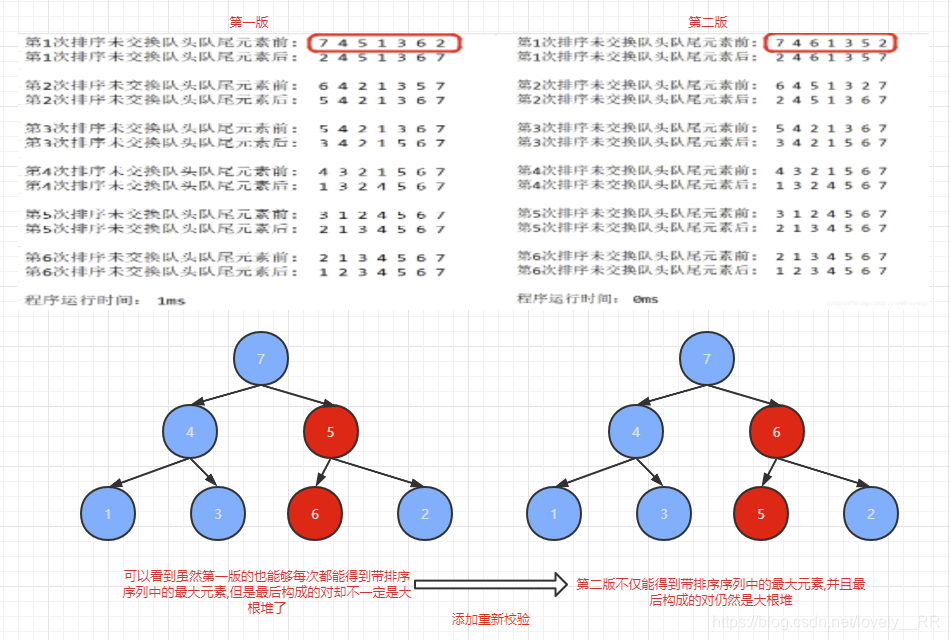
相信经过我这样的讲解之后,大家一定能够更好的理解堆排序了.
复杂度分析:
理解完堆排序的基本思想之后,我们就需要来分析一下他的时间复杂度,空间复杂度.
-
时间复杂度
堆排序的本质思想也是利用了二叉树的特性,所以根据他的遍历次数以及二叉树的层数可以得到堆排序的时间复杂度为
O(N*logn),不仅仅是平情况是这样最好与最坏的情况都是如此. -
空间复杂度
这个我们可以看到我们整个排序的过程中只增加一个存储交换元素的
temp,所以堆排序的空间复杂是常量级别的仅为O(1).
2-计数排序
算法思想:
计数排序最核心的思想就是计数序列中每个元素出现的次数,我们将每个元素的数量都记录下来之后.我们就可以通过按
了解完计数排序的基本思想之后,我们就来看看看这个算法的实现步骤又是怎么样的呢?主要就是下面这几个步骤:
-
1.第一次遍历序列,找出序列中的最大值以及最小值,然后根据
最大值MAX与最小值MIN创建一个MAX-MIN+1长度的数组.为什么创建这样长度的数组呢,因为只有创建了这样长度的数组,MIN-MAX区间内的每个元素才有对应的位置进行存放,如下图所示:
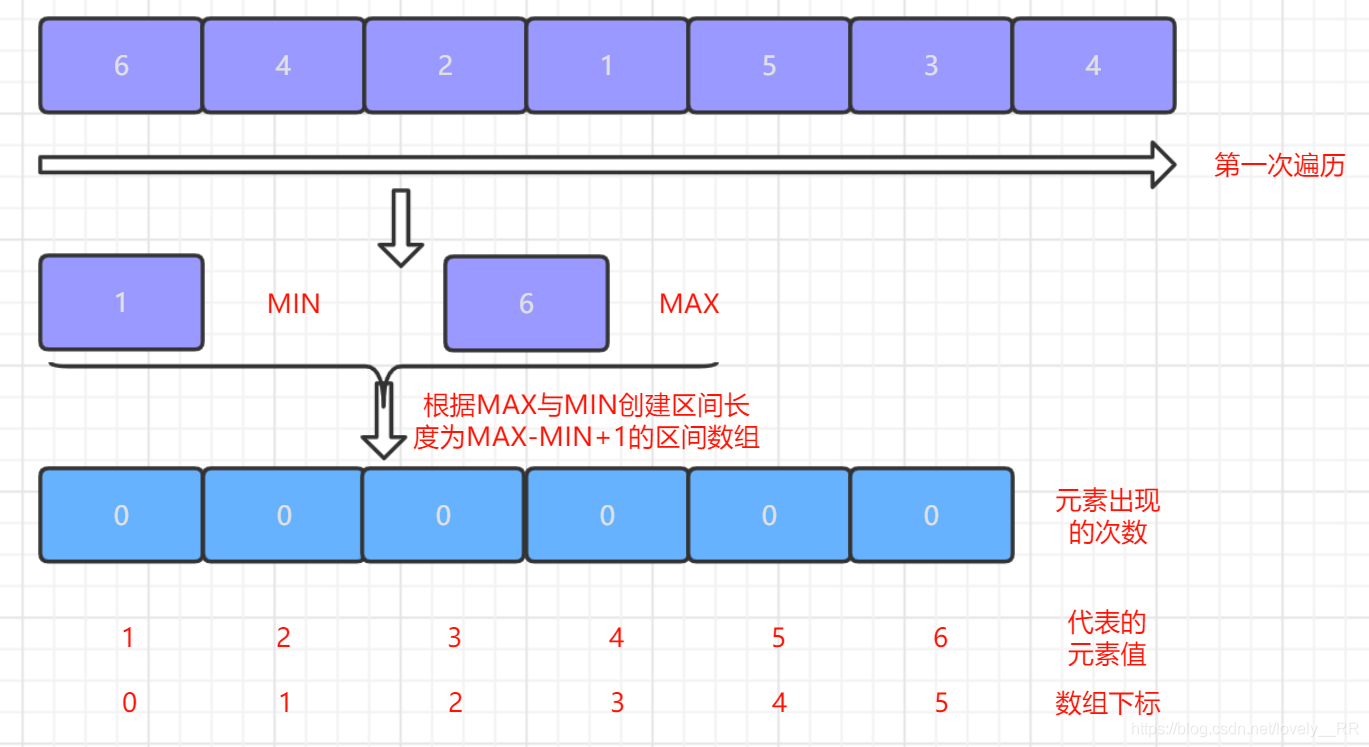
-
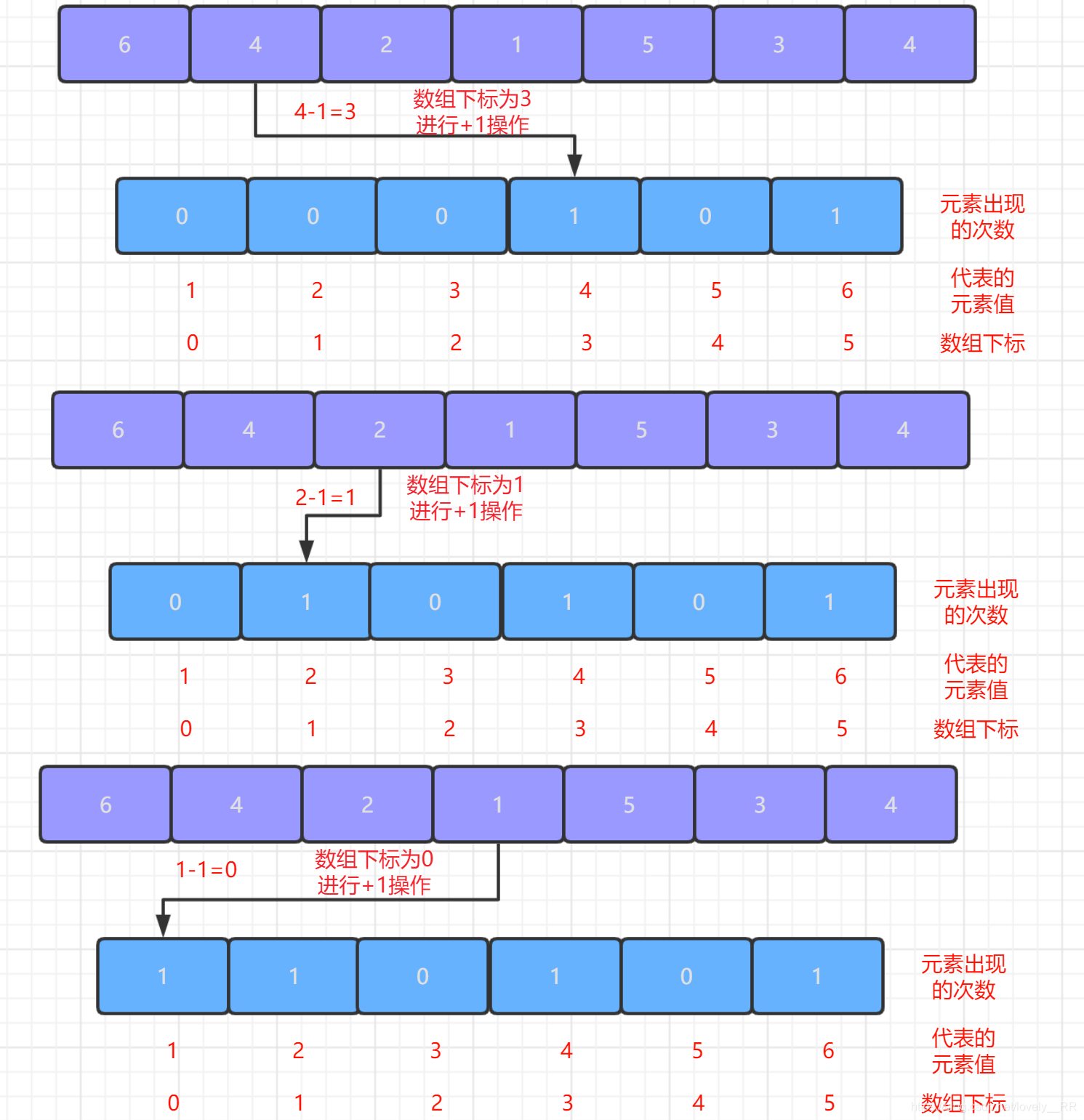
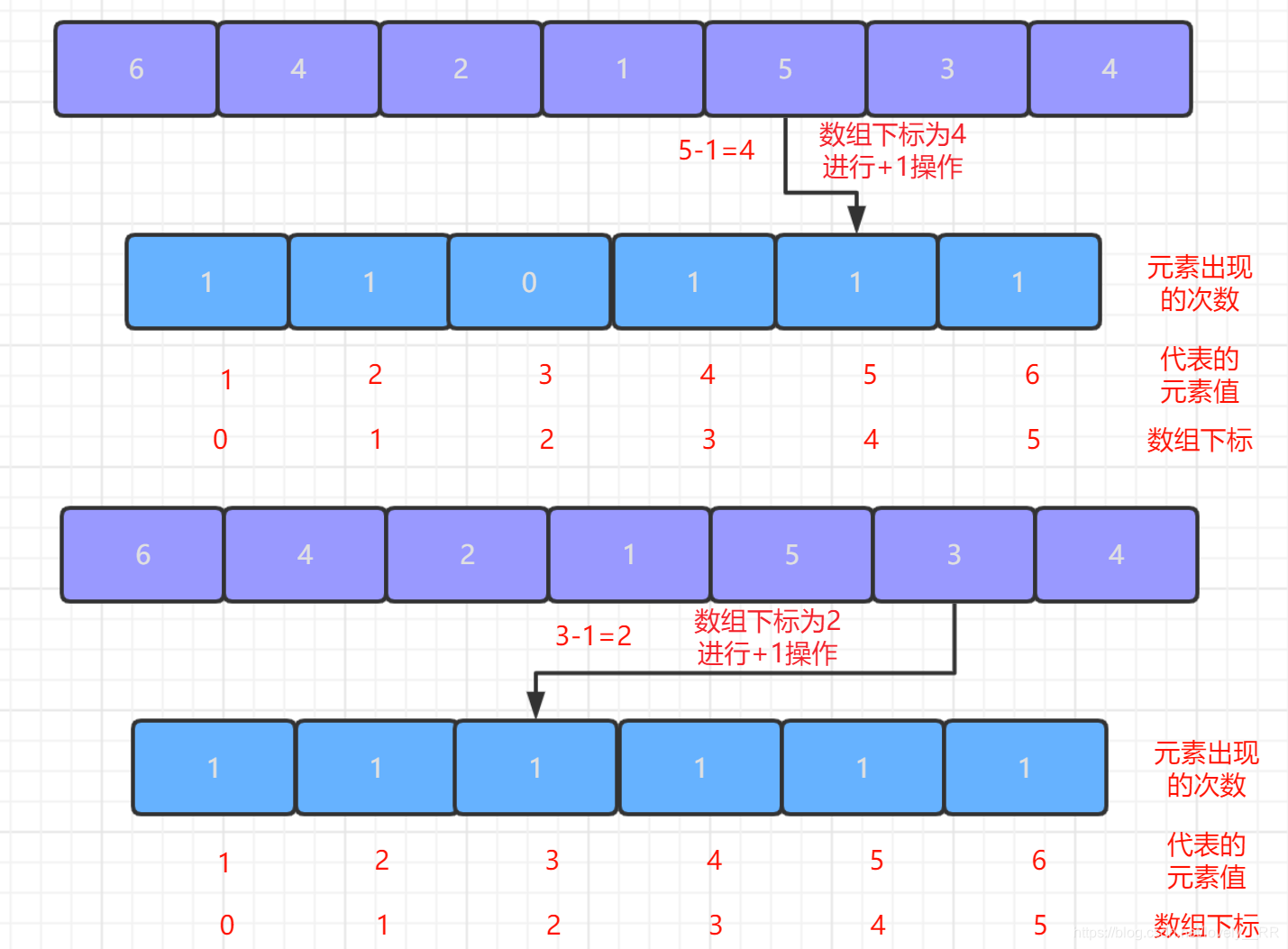
2.第二次遍历序列,我们每次遍历一个元素都将该元素所对应的区间数组对应的位置进行
+1操作,这个步骤其实就是我们计数排序的核心----计数了.遍历结束之后,区间数组中的元素值就代表相应元素出现的次数,如下图所示:
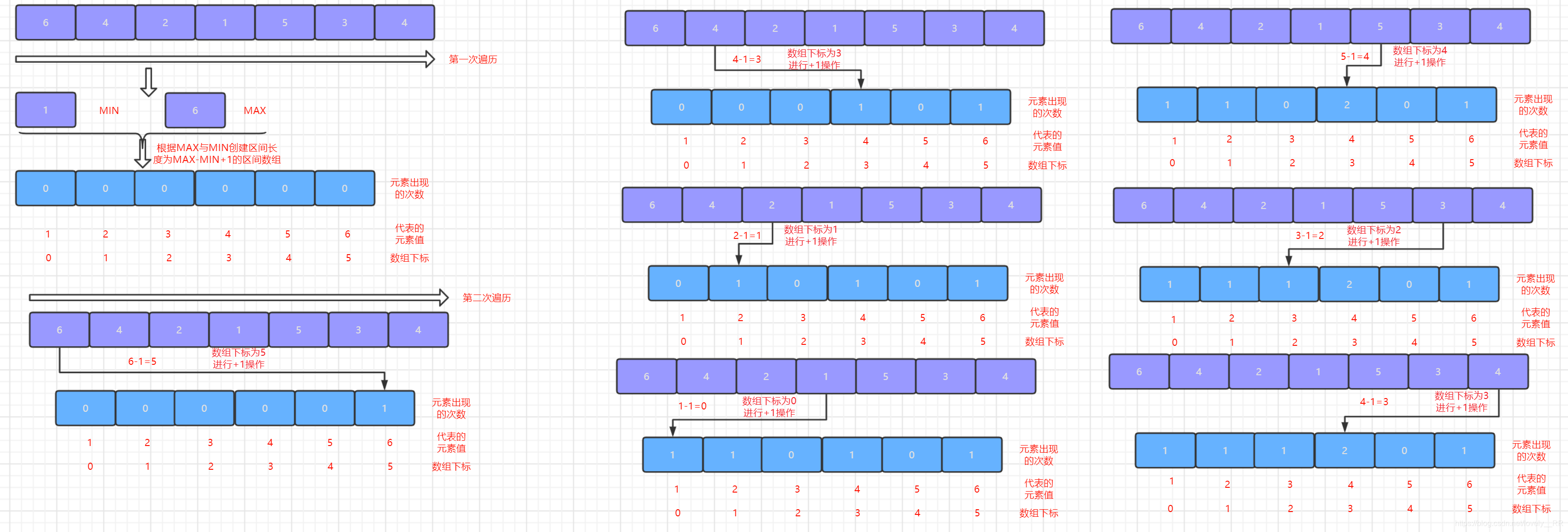
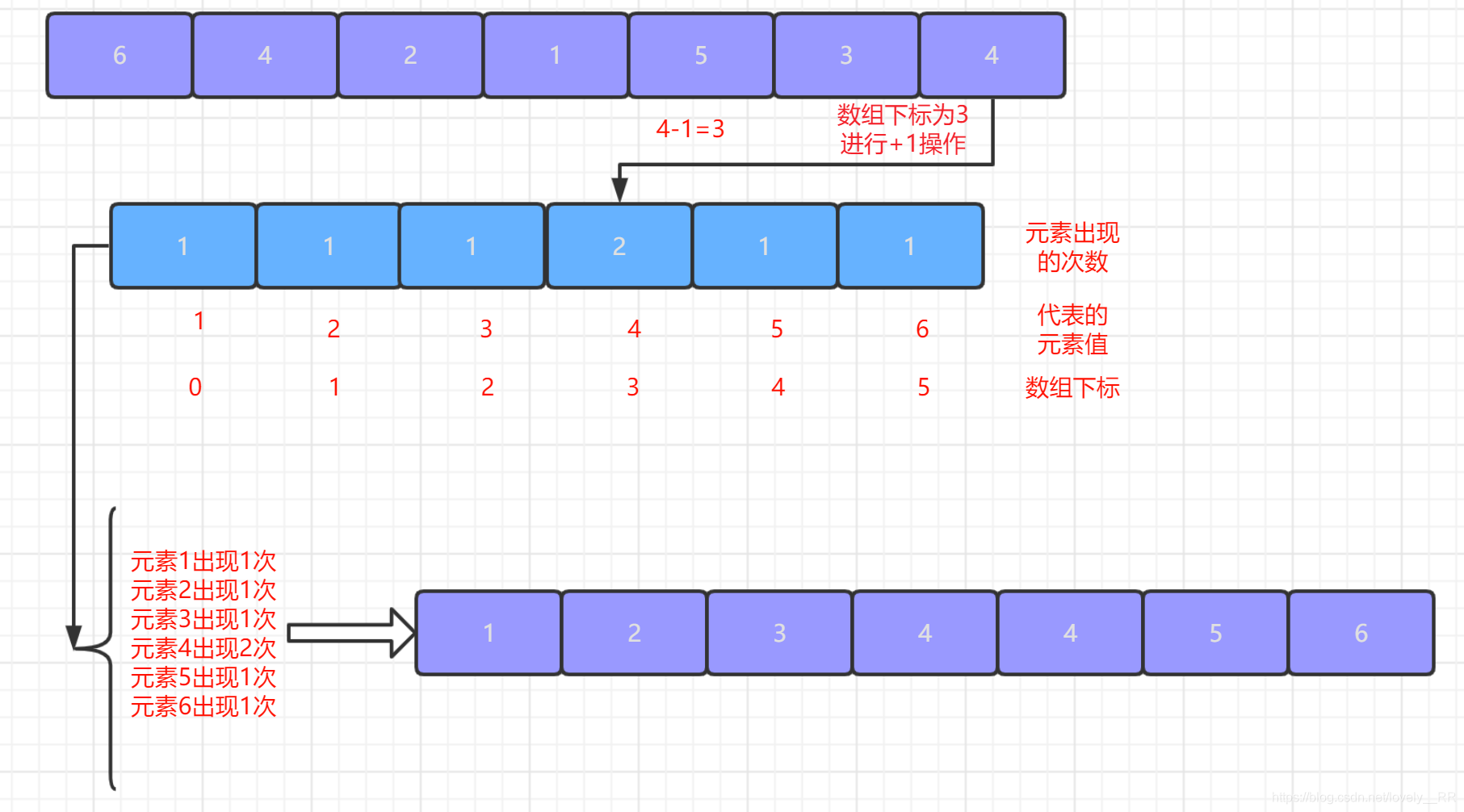
-
3.最后一步就只需要按照区间数组中的次数一次将该元素打印出来即可.如下图所示:
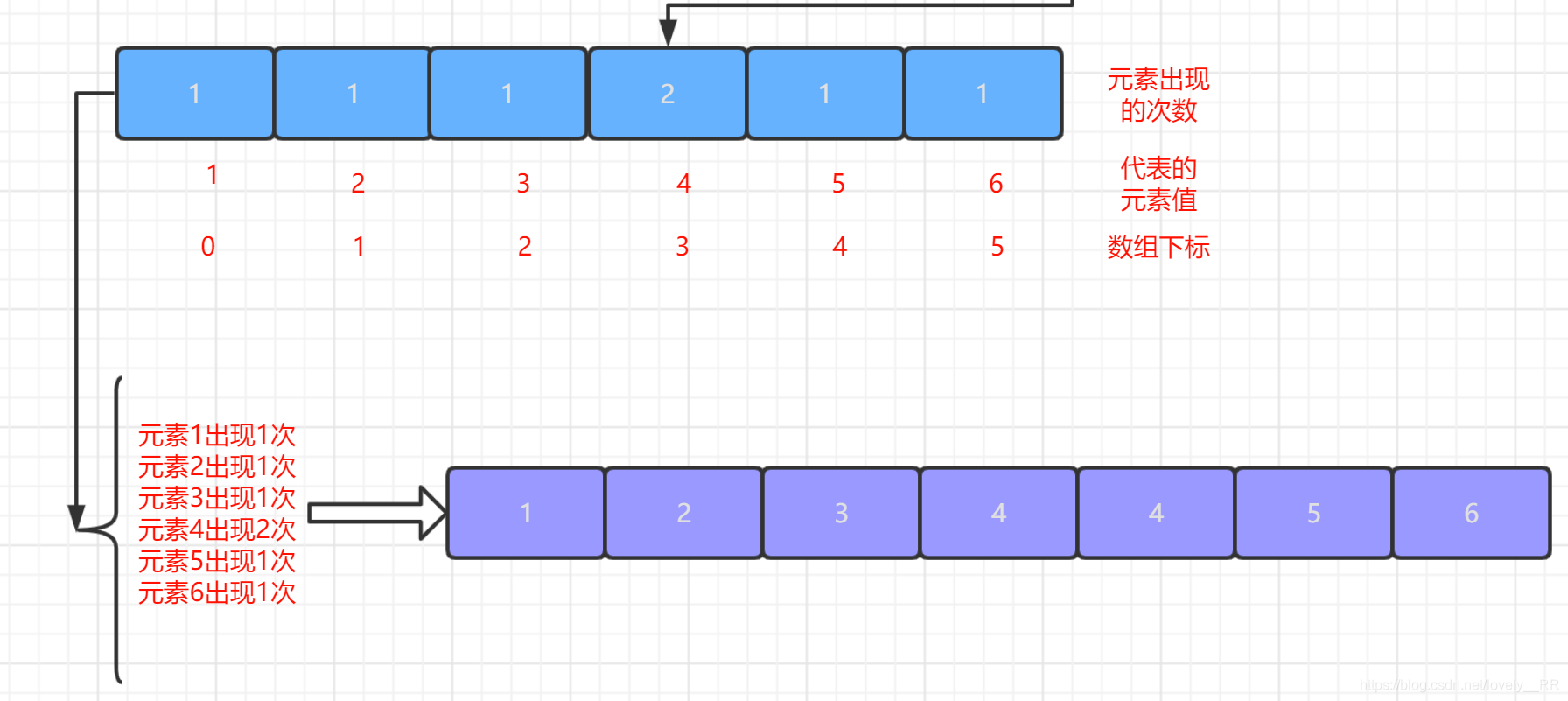
计数排序的基本思想基本就是这样,按照惯例,还是通过下面的图来帮助大家更好的理解计数排序的基本思想:
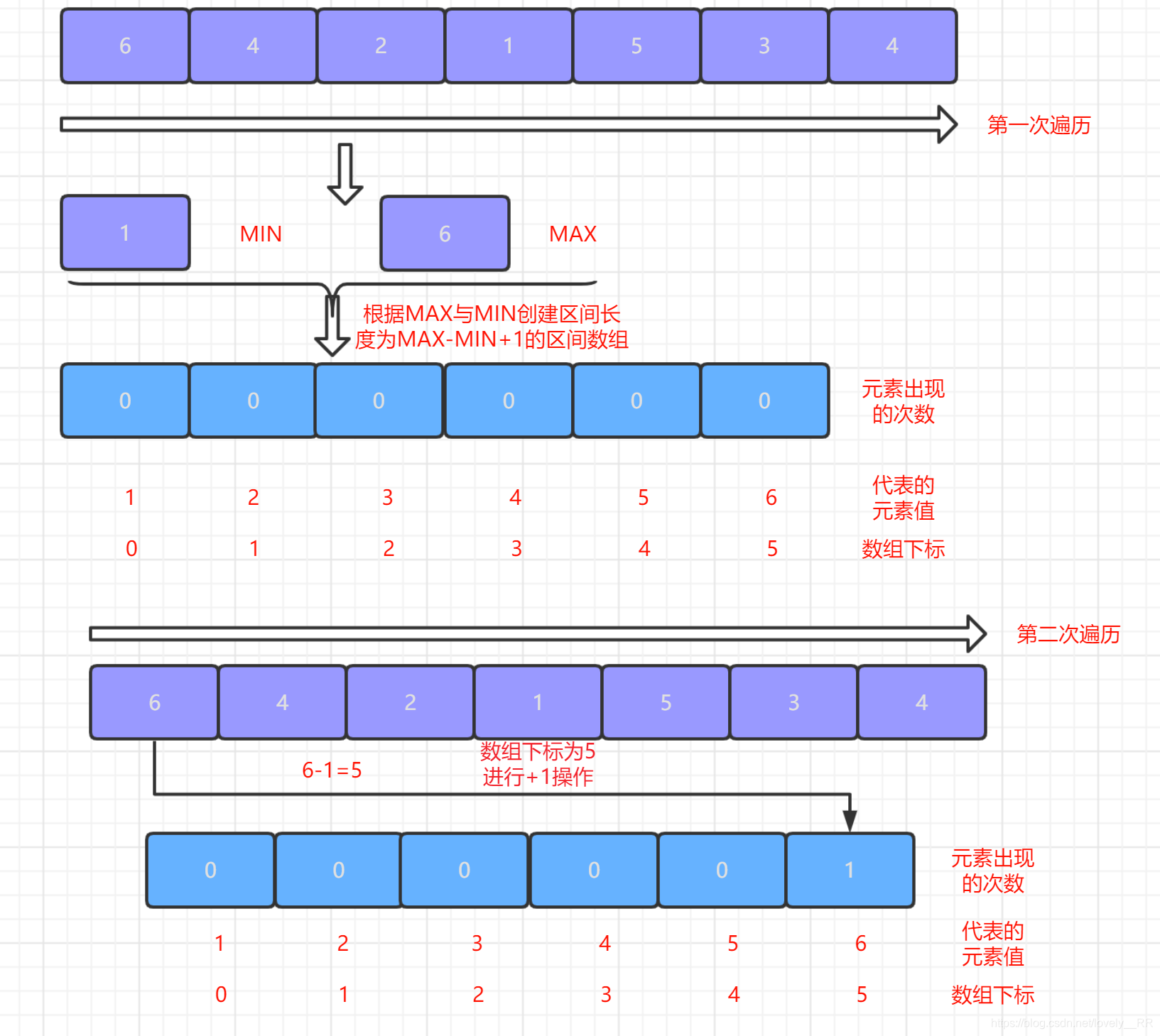
了解完计数排序的基本思想之后,我们还是按照惯例分析一下计数排序算法的一些特点:
-计数排序是稳定的 ,这个大家应该能很明显的看出来,因为计数排序本身并不是基于比较的算法.
-计数排序需要的额外空间比较大,这个大家很明显的看出来,并且空间浪费的情况也会比较严重,因为一旦序列中MAX与MIN的差距过大,那么需要的内存空间就会非常大.并且假如序列中的元素都是散布在一个特定的区间内,那么内存空间浪费的情况也会非常明显.
算法图解:
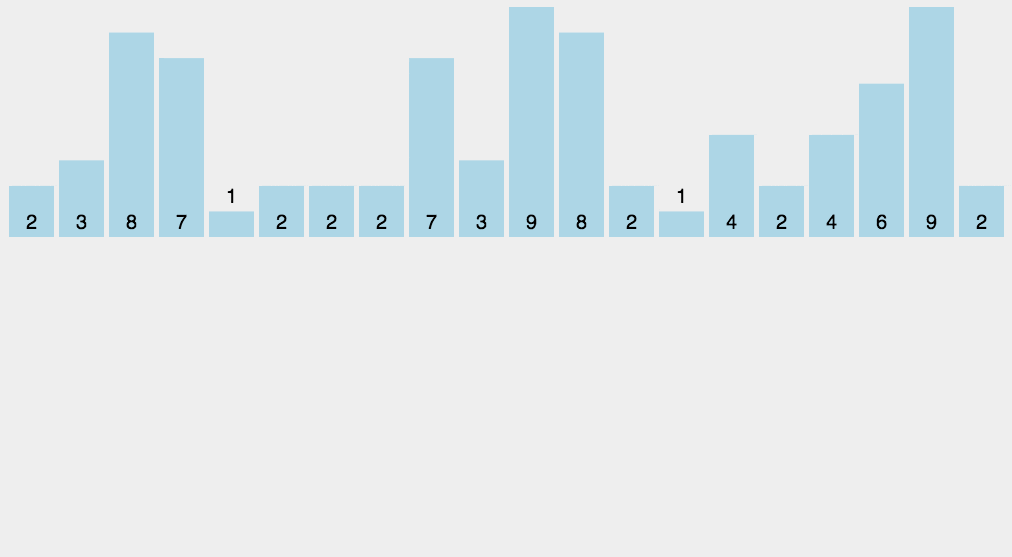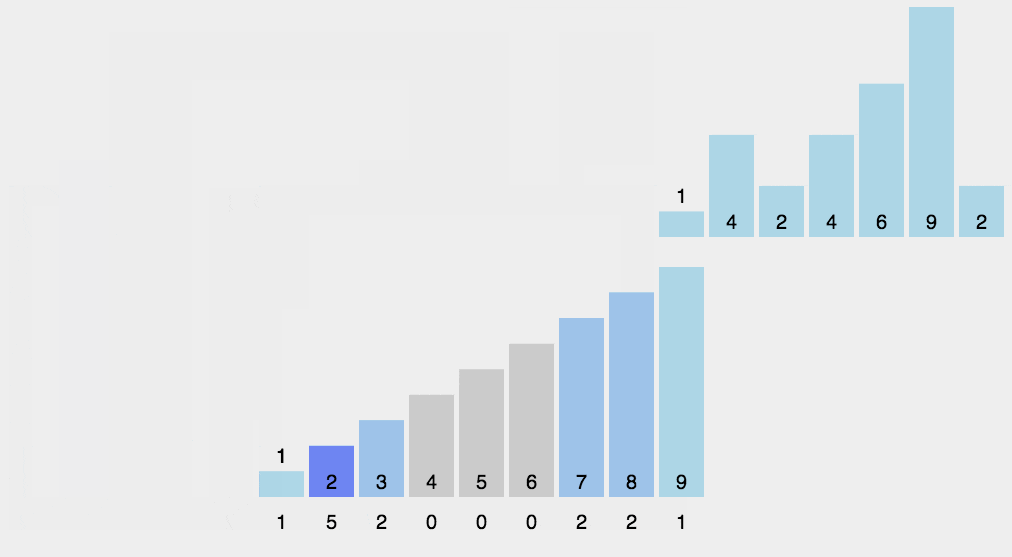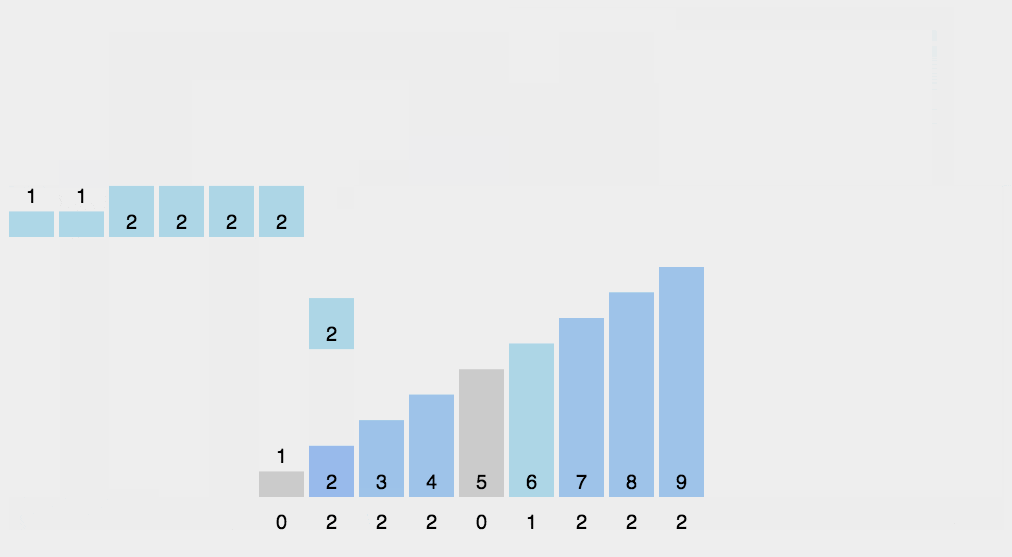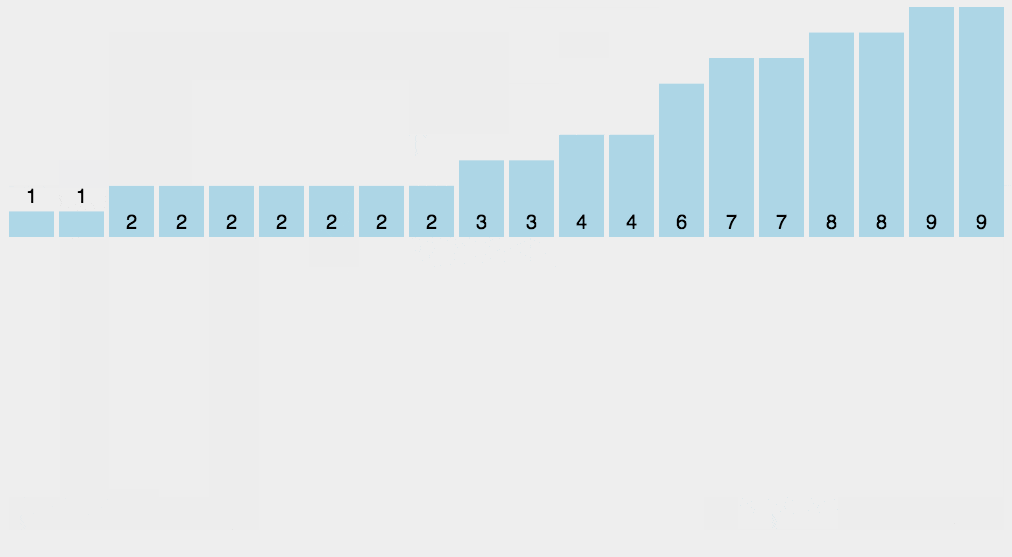
示例代码:
public static void main(String[] args) { int []num ={7,4,9,3,2,1,8,6,5,10}; long startTime=System.currentTimeMillis(); int min=Integer.MAX_VALUE; int max=Integer.MIN_VALUE; //先找出数组中的最大值与最小值 for(int i=0;i<num.length;i++) { if(num[i]<min) min=num[i]; if(num[i]>max) max=num[i]; } //创建一个长度为max-min+1长度的数组来进行计数 int []figure=new int [max-min+1]; for(int i=0;i<num.length;i++) { //计算每个数据出现的次数 figure[num[i]-min]++; } int begin=0; //创建一个新的数组来存储已经排序完成的结果 int []num1=new int [num.length]; for(int i=0;i<figure.length;i++) { //循环将数据pop出来 if(figure[i]!=0) { for(int j=0;j<figure[i];j++) { num1[begin++]=min+i; } } } System.out.println("数据范围:"+min+"~"+max); System.out.println("计数结果: "); for(int i=0;i<num.length;i++) System.out.println(" "+num[i]+"出现"+figure[num[i]-min]+"次"); System.out.print("排序结果: "); for(int i=0;i<num1.length;i++) System.out.print(num1[i]+" "); System.out.println(); long endTime=System.currentTimeMillis(); System.out.println("程序运行时间: "+(endTime-startTime)+"ms"); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40

复杂度分析:
理解完计数排序的基本思想之后,我们就需要来分析一下他的时间复杂度,空间复杂度.
-
时间复杂度
计数排序很明显是一种通过空间来换时间的算法,因为我们可以很明显的看到计数排序需要三次遍历,两次遍历我们的原序列,第三次是遍历我们的区间数组.那么很明显
时间复杂度一定是线性级别的但是因为第三次遍历的并不是我们的原序列,而是我们的区间数组,所以时间复杂度并不是我们的平常的O(n),而是应该加上我们遍历区间数组的时间,假设我们的区间数组长度为k的话,那么我们的时间复杂度就是O(n+k) -
空间复杂度
上面我们已经说过了,计数排序本身就是一个通过空间来换取时间的算法,所以很明显他的空间复杂度就会很高.并且这个空间复杂度主要就取决于我们区间数组的长度,所以假设我们的区间数组长度为k的话,那么我们的空间复杂度就为
O(k)
3-桶排序
算法思想:
大家第一眼看到这个算法的名字时相信大家的反应应该和我是一样的,桶排序?排序怎么还需要用到桶呢?桶排序里的桶又是主要是干什么的呢?
其实这个大家类比到我们平常生活中就能基本知道桶排序的桶是干嘛的呢?在我们的日常生活中,我们的桶一般都是用来装东西的,我们可能是用来装水,又或者是装钱的反正不管怎么样,我们的桶最后都是一个容器,是用来存储相应的物质的.

显然我们当前存在的只有我们的待排序的序列,那么我们的桶就是用来存储我们的序列中的元素的.就像下图所示:
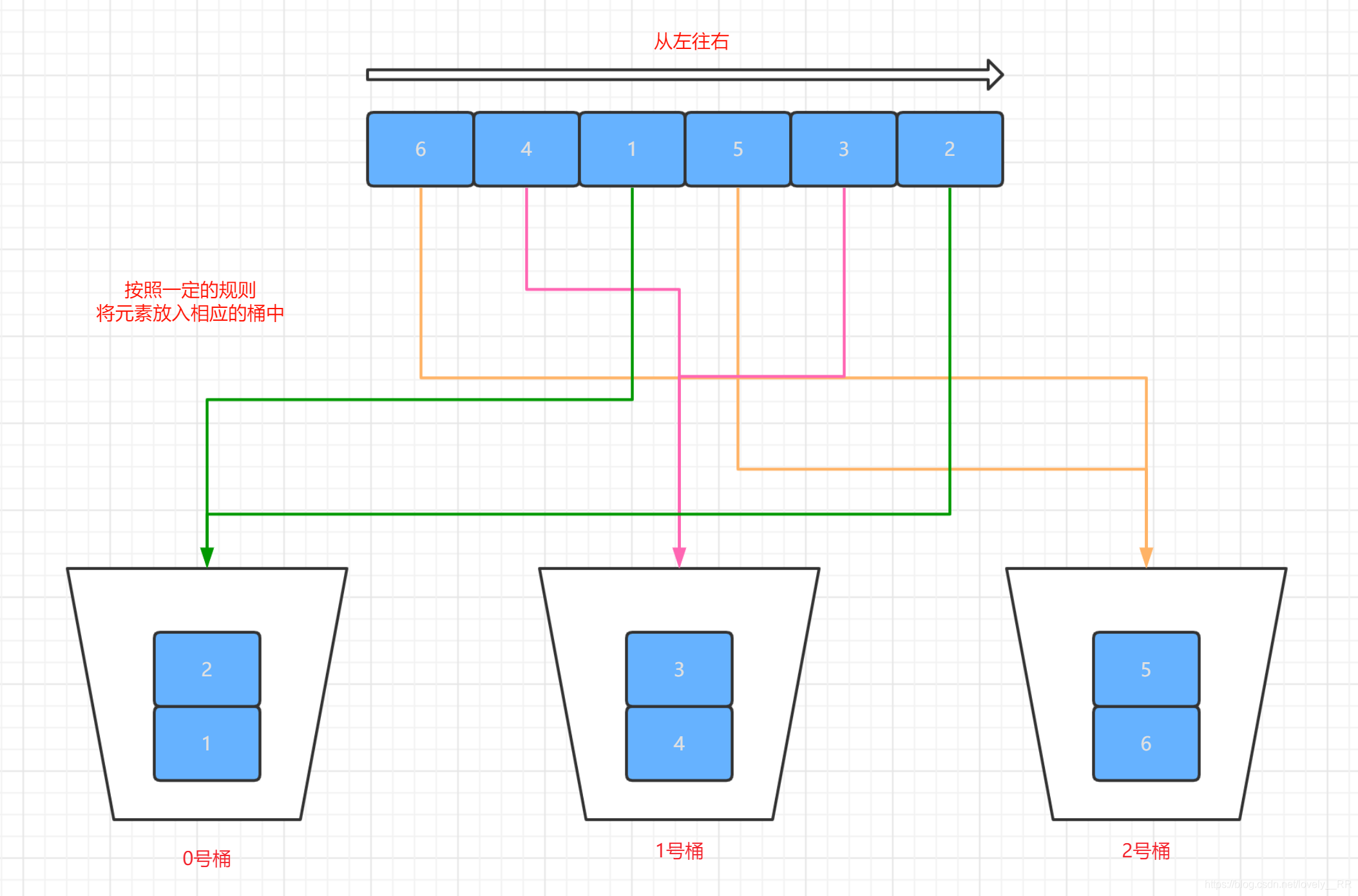
可以看到我们把相应的元素放入相应的桶里面了.这个放入的规则是这样的:桶是从大到小排列的,并且每一个桶都会有一个数据范围,意思就是0号桶存放是1~ 2数据范围的数据,1号桶存放3~4数据范围的数据,2号桶存放吧5 ~6数据范围内的数据.详细的放入规则我会在下面的实现步骤里面说.这里大家先简单了解一下.
这里大家要注意的一点就是,我们在把元素放入各自相应的桶里面的时候,是需要对桶内的序列进行排序的,意思就是等到每个元素都放入相应的桶里面之后,桶里面相应的序列本身也已经有序了.就如下图所示:

可以看到上面,每个桶内的序列都已经排好序了,那么很显然我们最后就只需要按照桶的序号大小将桶内的元素打印出来,那么我们的序列就已经排好序了.
说完桶排序的基本思想之后,我们接下来就说一下桶排序在代码上是如何实现的,大致有下面这几步:
-
1.我们首先需要第一次遍历我们的序列,得到我们序列中的最大值
MAX以及序列中的最小值MIN,找到我们序列中的最大值与最小值之后,那么我们就可以确定序列中的所有都是在MIN~MAX这个数据范围区间之中. -
2.第二步我们就是需要根据序列的数据范围来确定我们到底需要几个桶来存放我们的元素,这一步其实是比较关键的,因为桶的数量太多或者太少都会降低桶排序的效率.
我们举两个例子:
假设我们桶的数量太少,就比如说只有一个桶:
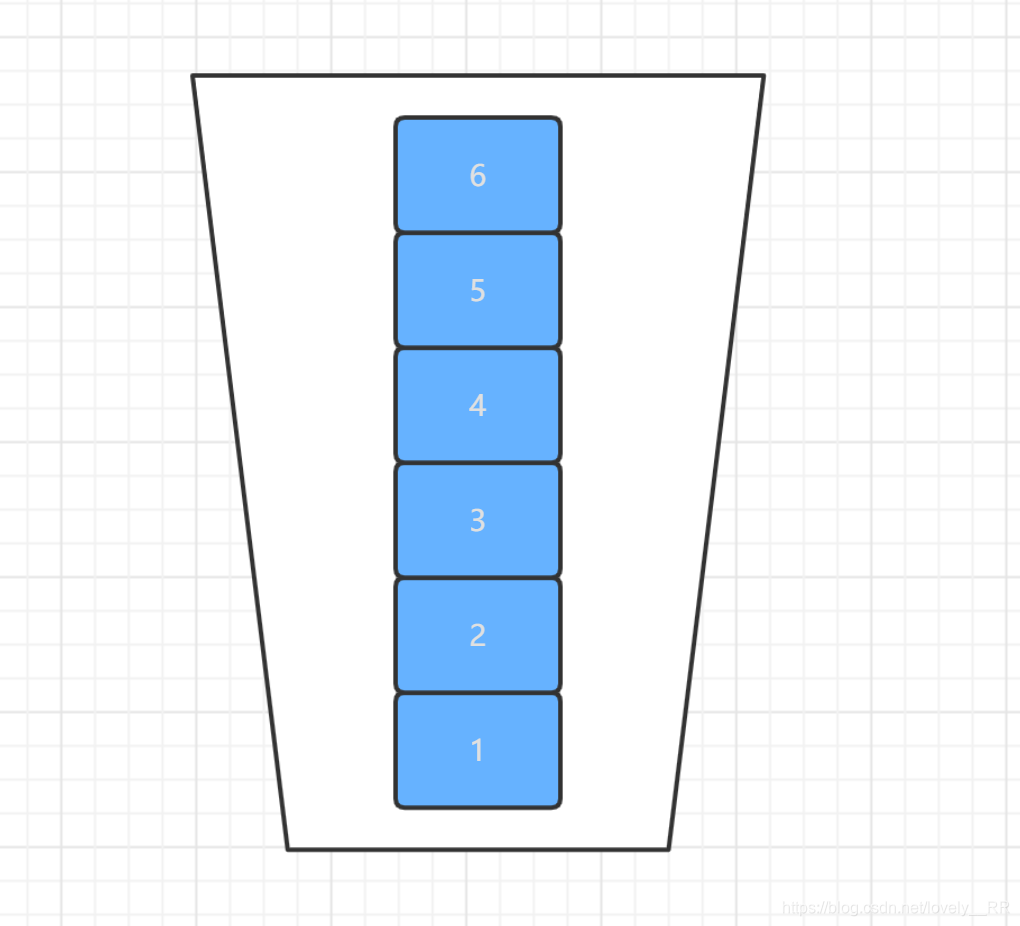
那么很显然我们的桶排序就又重新退化成我们前两篇内容里介绍的比较算法了.又假设我们桶的数量太多,就比如说有
MAX-MIN+1个桶:

那么很显然这时候的桶排序又重新退化成了我们上面刚刚讲解过的计数排序了.所以说我们需要确定好一个适中的桶的数量,不然回就会出现我们上面所说到的几种情况.但是有没有一个特定的公式来确定桶的数量.所以我们还是只能自己确定桶的数量.但是有一个规则我们还是可以考虑进去的,那就是
最好让元素平均的分散到每一个桶里. -
3.确定完桶的数量之后,我们就可以给每个桶来划分数据范围了.一般是这样划分的,
(MAX-MIN+1)/桶的数量,得到的结果就是桶长.之后每个桶的数据范围就通过桶的编号以及桶长就可以确定每个桶的数据范围.就如下面的公式:左闭右开
桶的数据范围=[MIN+(桶的编号-1)*桶长,MIN+桶的编号 *桶长)
有了每个桶的数据范围时候,我们第二次遍历序列将每个元素存到相应的桶里面了.这个过程我们要注意,在往桶里面添加元素的时候,就需要在每个桶里面将元素排好序. -
4.当我们第二次遍历结束之后,我们就只需要按照桶的编号,在将该编号的桶里面的元素打印出来,桶排序就已经完成了.
接下来我们还是通过下面的图来动态演示一下桶排序的过程:
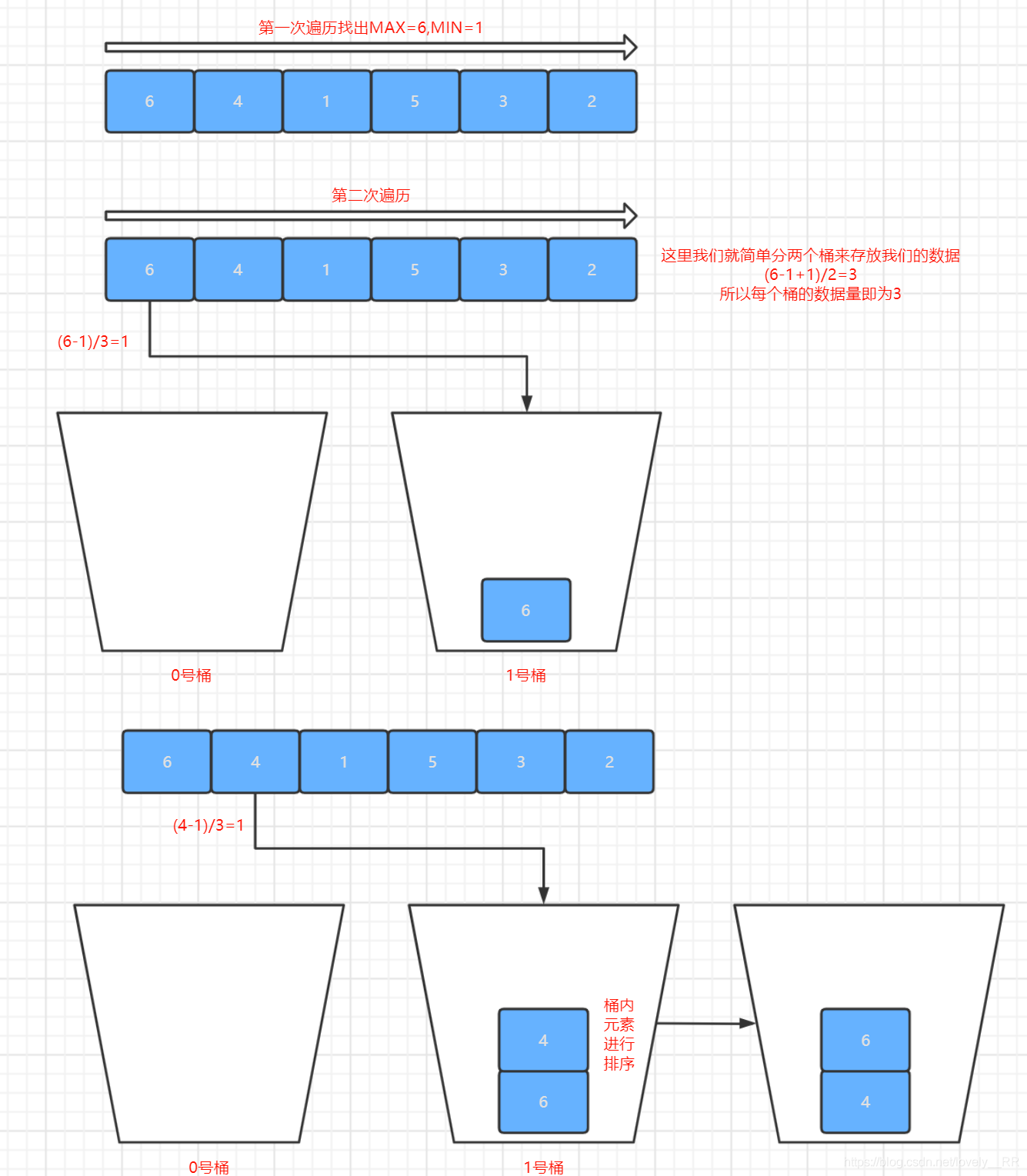
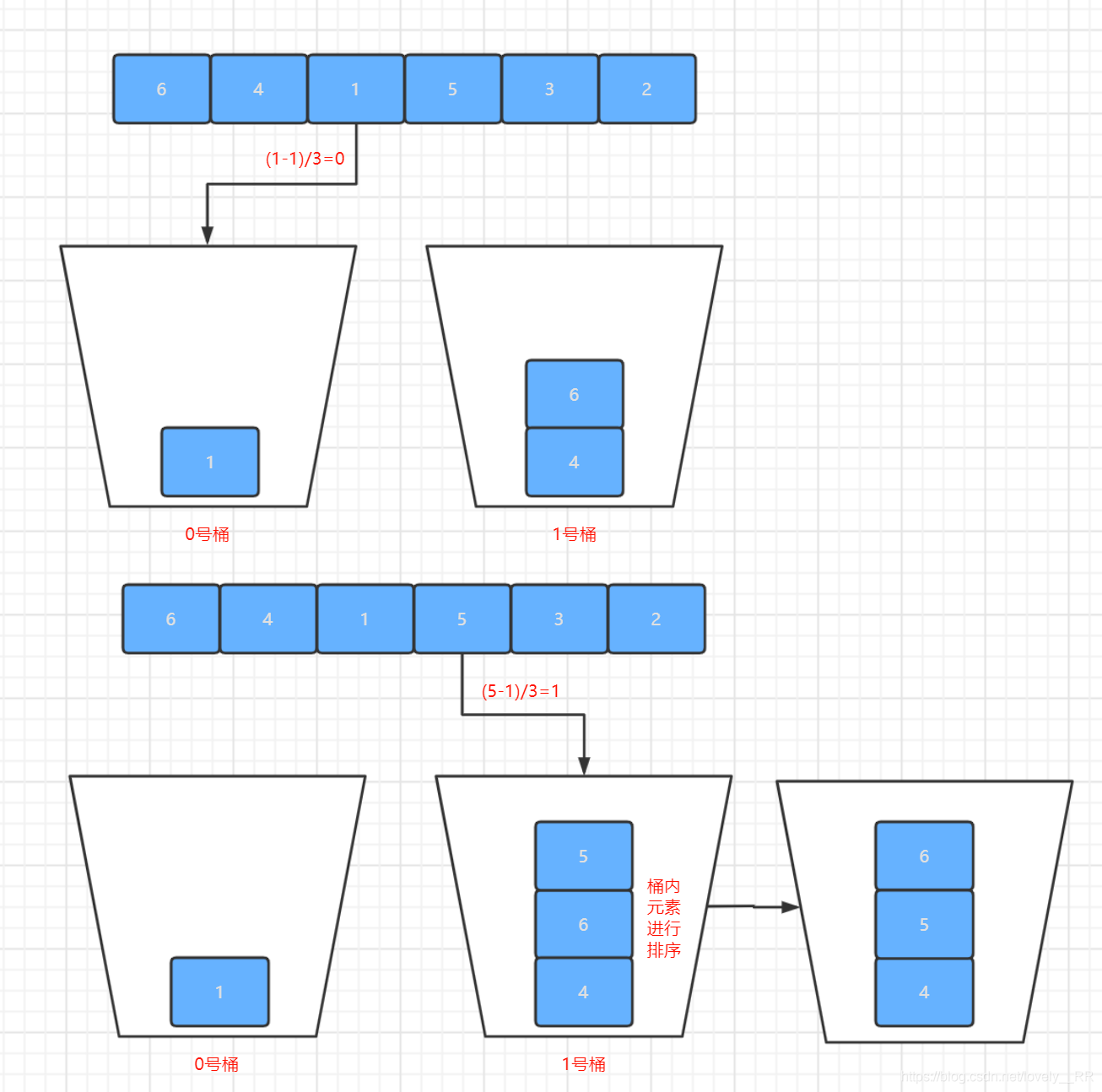
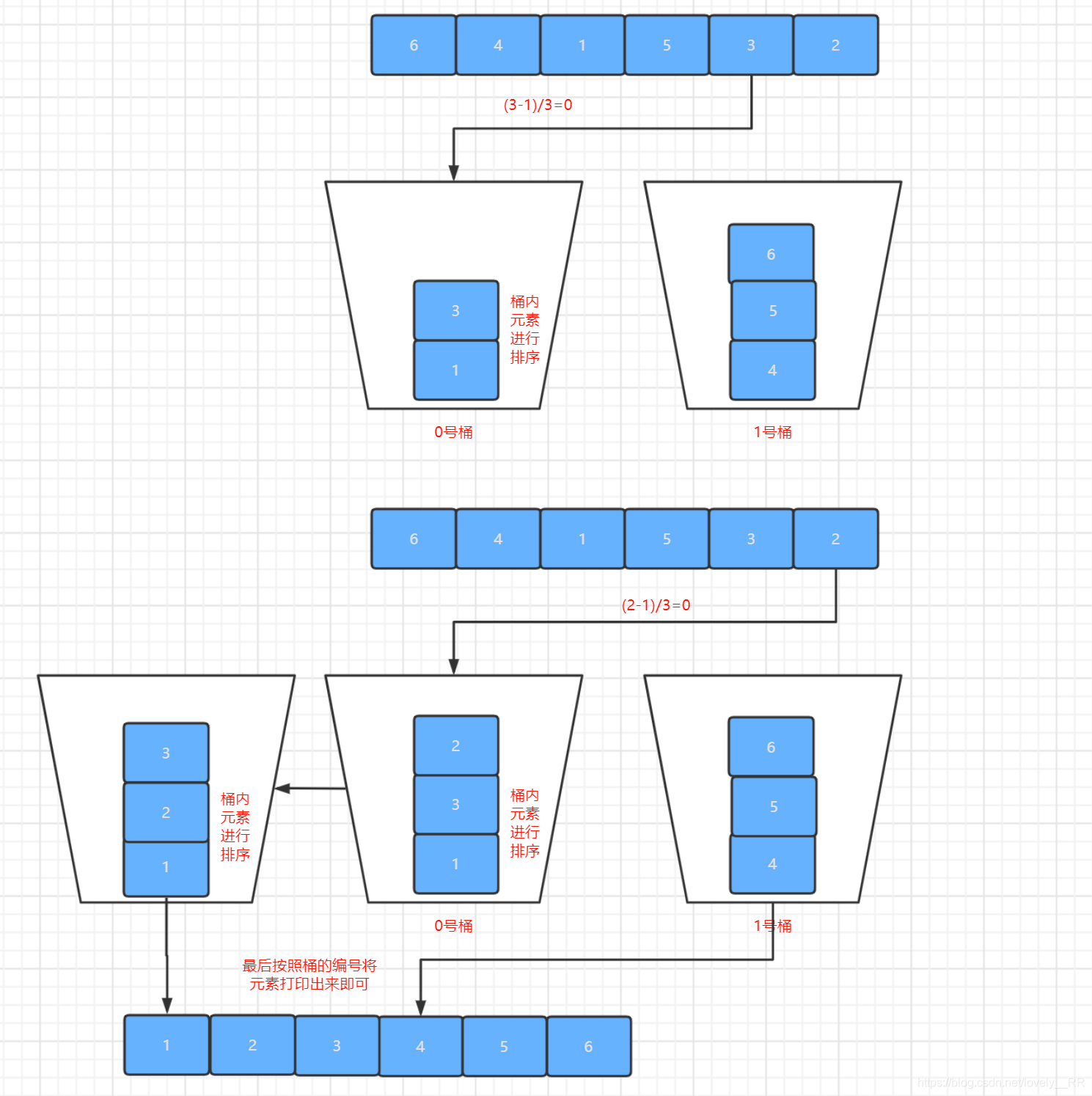
了解完桶排序的基本思想之后,按照惯例我们还是来简单分析一下他的一些特点:
- 桶排序是
稳定的,原因和上面计数排序的理由是一样的. - 桶排序也是一个
通过空间换取时间的算法,但是他的空间复杂度是可以控制的.就像我们上面说的主要就是控制桶的数量.如果桶的数量设置的合理,既能降低时间复杂度,也能降低空间复杂度.
算法图解:

示例代码:
//在链表中添加元素的同时需要进行元素的排序 public static void sort(ArrayList<Integer>list,int i) { if(list==null) list.add(i); //这里采用的排序方式为插入排序 else { int flag=list.size()-1; while(flag>=0&&list.get(flag)>i) { if(flag+1>=list.size()) list.add(list.get(flag)); else list.set(flag+1, list.get(flag)); flag--; } if(flag != (list.size()-1)) //注意这里是flag+1,自己可以尝试将这里换成flag看看,会出现数组越界的情况 list.set(flag+1, i); else list.add(i); } } public static void Bucketsort(int []num,int sum) { //遍历得到数组中的最大值与最小值 int min=Integer.MAX_VALUE; int max=Integer.MIN_VALUE; for(int i=0;i<num.length;i++) { min = min <= num[i] ? min: num[i]; max = max >= num[i] ? max: num[i]; } //求出每个桶的长度,这里必须使用Double double size=(double)(max-min+1)/sum; ArrayList<Integer>list[]=new ArrayList[sum]; for(int i=0;i<sum;i++) { list[i]=new ArrayList<Integer>(); } //将每个元素放入对应的桶之中同时进行桶内元素的排序 for(int i=0;i<num.length;i++) { System.out.println("元素:"+String.format("%-2s", num[i])+", 被分配到"+(int)Math.floor((num[i]-min)/size)+"号桶"); sort(list[(int)Math.floor((num[i]-min)/size)], num[i]); } System.out.println(); for(int i=0;i<sum;i++) { System.out.println(String.format("%-1s", i)+"号桶内排序:"+list[i]); } System.out.println(); //顺序遍历各个桶,得出我们 已经排序号的序列 for(int i=0;i<list.length;i++) { if(list[i]!=null){ for(int j=0;j<list[i].size();j++) { System.out.print(list[i].get(j)+" "); } } } System.out.println(); System.out.println(); } public static void main(String[] args) { int []num ={7,4,9,3,2,1,8,6,5,10}; long startTime=System.currentTimeMillis(); //这里桶的数量可以你自己定义,这里我就定义成了3 Bucketsort(num, 3); long endTime=System.currentTimeMillis(); System.out.println("程序运行时间: "+(endTime-startTime)+"ms"); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65

这里的时间是不准确的,因为我需要将每轮排序的结果打印出来给大家看,所以会多花费一些时间,如果大家想要看真实的时间的话,大家可以把我打印结果的代码注释掉再看看算法的执行时间.
复杂度分析:
理解完桶排序的基本思想之后,我们就需要来分析一下他的时间复杂度,空间复杂度.
-
时间复杂度
桶排序的时间复杂度和上面的计数排序是一样的,同样也是线性级别的,但是也是增加了桶的时间,所以也是
O(n+k) -
空间复杂度
上面我们已经说过了,桶排序本身也是一个通过空间来换取时间的算法,所以很明显他的空间复杂度就会很高.并且这个空间复杂度主要就取决于桶的数量以及桶的范围,所以假设有k个桶的话,那么空间复杂度就为
O(n+k)
4-基数排序
算法思想:
基数排序的实现步骤非常好理解,但是想要真正理解他的算法思想就稍微有点难度了.那么接下来就来讲解基数排序的算法思想.
首先基数排序是根据数位来进行排序的.他是从个位开始,然后按照每一位的数进行排序,如下图所示:
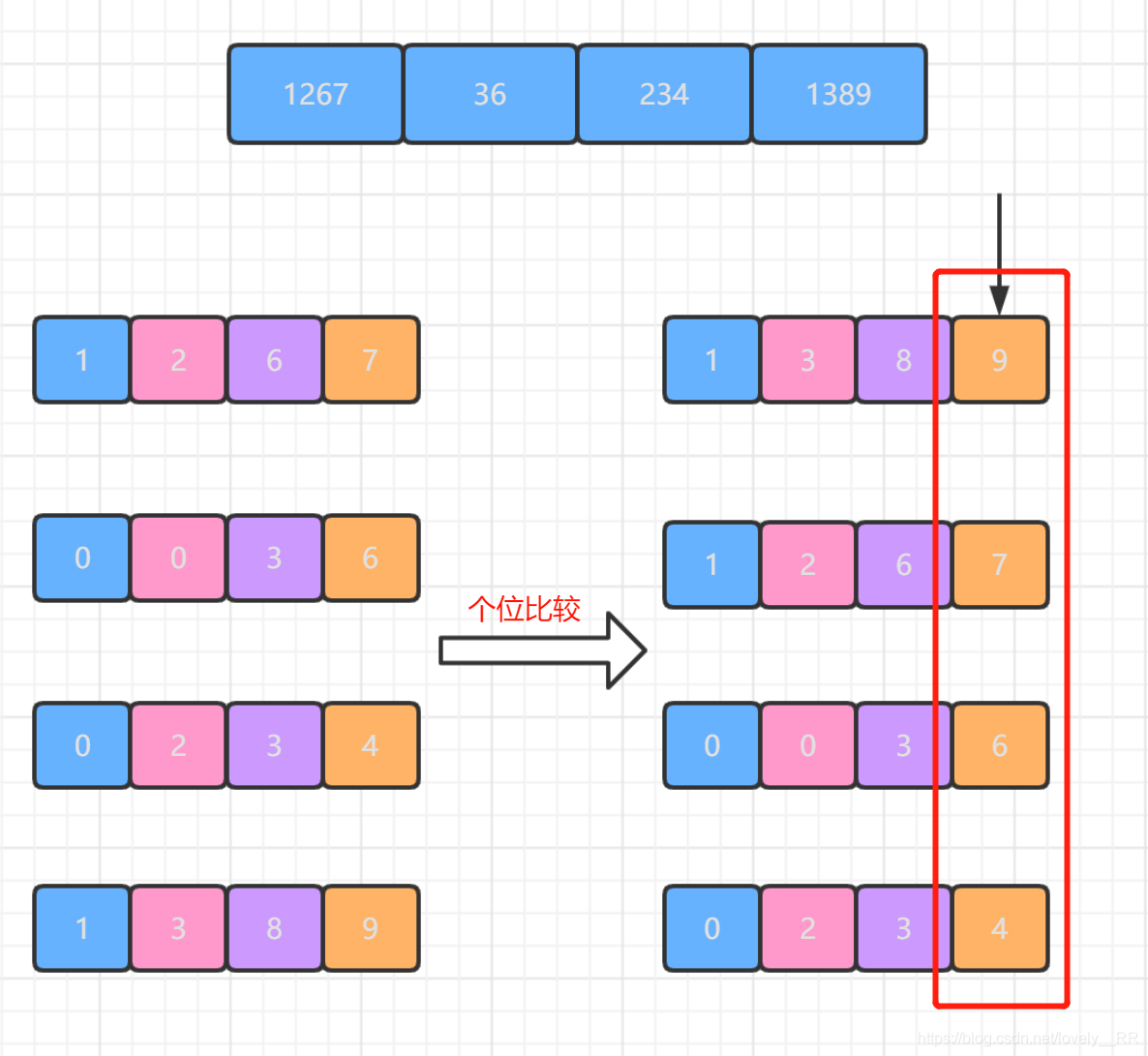
排完序之后就往前进一位,然后再将所有的数按照这一位所在的数进行排序,如下图所示:

重复这个过程直到所有的位数都已经被排过序了.如下图所示:
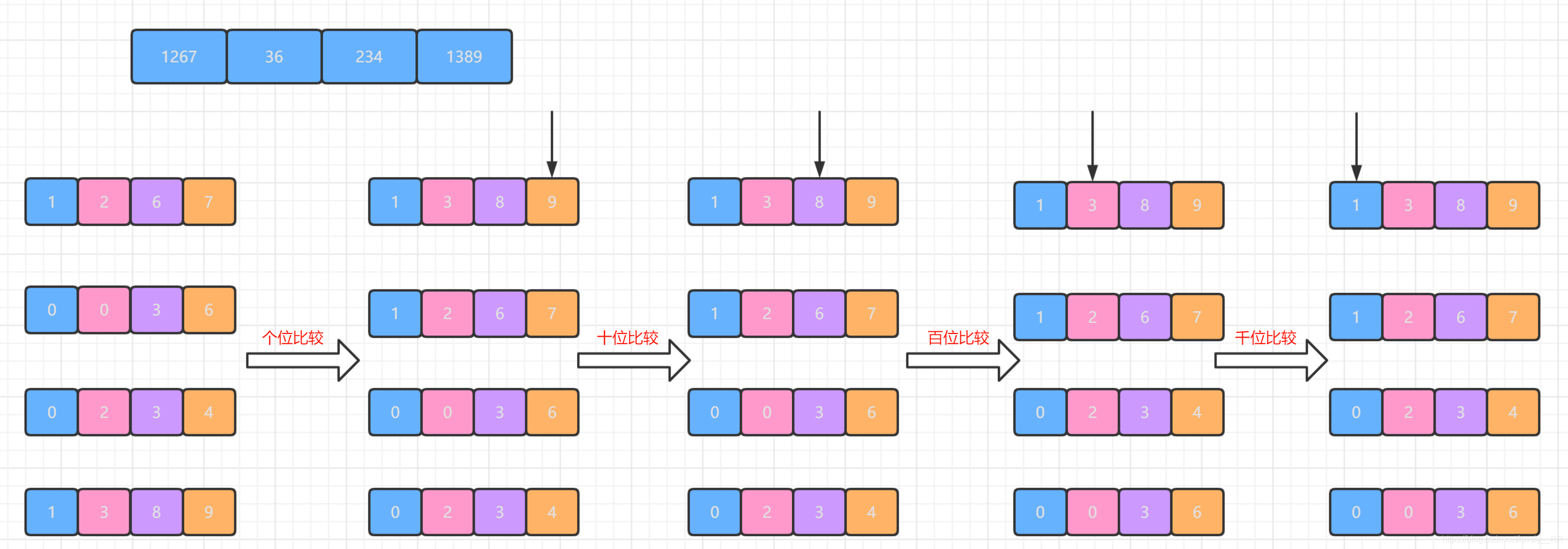
并且如果这个过程中碰到某个数在这个为上没有数的话就进行补零操作,将该位看成是0.就比方下图我用红框圈出来的部分:
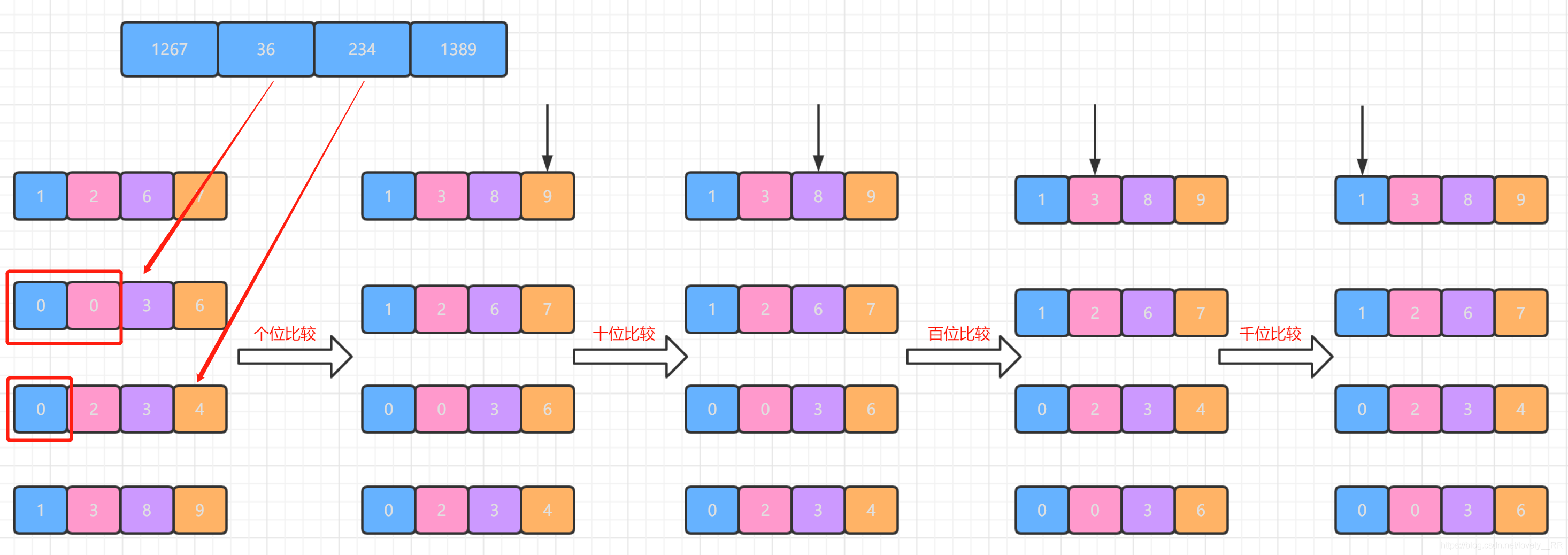
等到所有的位数都已经排序完毕之后,我们就可以看到我们已经排序好的序列了.
这个过程相信大家肯定都很好理解,但是相信大家如果是第一次看这个算法的肯定会有和我当初一样的困惑,那就是为什么基数排序选择的是从低位到高位来进行排序的呢,而不是像我们平常比较数据的大小一样,从高位到低位来比较呢?
这里呢我们先不讲为什么,我们先看下面这两个案例:
- 从高位到低位进行比较
| 原序列 | 百位排好序后 | 十位排好序后 | 个位排好序后 |
|---|---|---|---|
| 329 | 839 | 657 | 839 |
| 457 | 720 | 457 | 329 |
| 657 | 657 | 355 | 657 |
| 839 | 457 | 839 | 457 |
| 436 | 436 | 436 | 436 |
| 720 | 329 | 720 | 355 |
| 355 | 355 | 329 | 720 |
- 从低位到高位进行比较
| 原序列 | 个位排好序后 | 十位排好序后 | 百位排好序后 |
|---|---|---|---|
| 329 | 720 | 720 | 329 |
| 457 | 355 | 329 | 355 |
| 657 | 436 | 436 | 436 |
| 839 | 457 | 839 | 457 |
| 436 | 657 | 355 | 657 |
| 720 | 329 | 451 | 720 |
| 355 | 839 | 657 | 839 |
对比看了上面两个例子之后相信大家就知道了,很明显我们看到如果是从该我到低位来进行比较的话,我们会发现比较到最后之后序列仍然是无序的,但是从低位到高位进行比较的话,我们就会发现序列到最后已经排好序了.
是不是很奇怪,同样的执行过程,只不过执行的顺序发生了改变,为什么结果就回产生这样的结果呢?产生这个差异的重点就是在我们忽略了一个问题,那就是我们在进行高位到低位比较的时候,高位的权重是高于低位的.就比方下图所示:
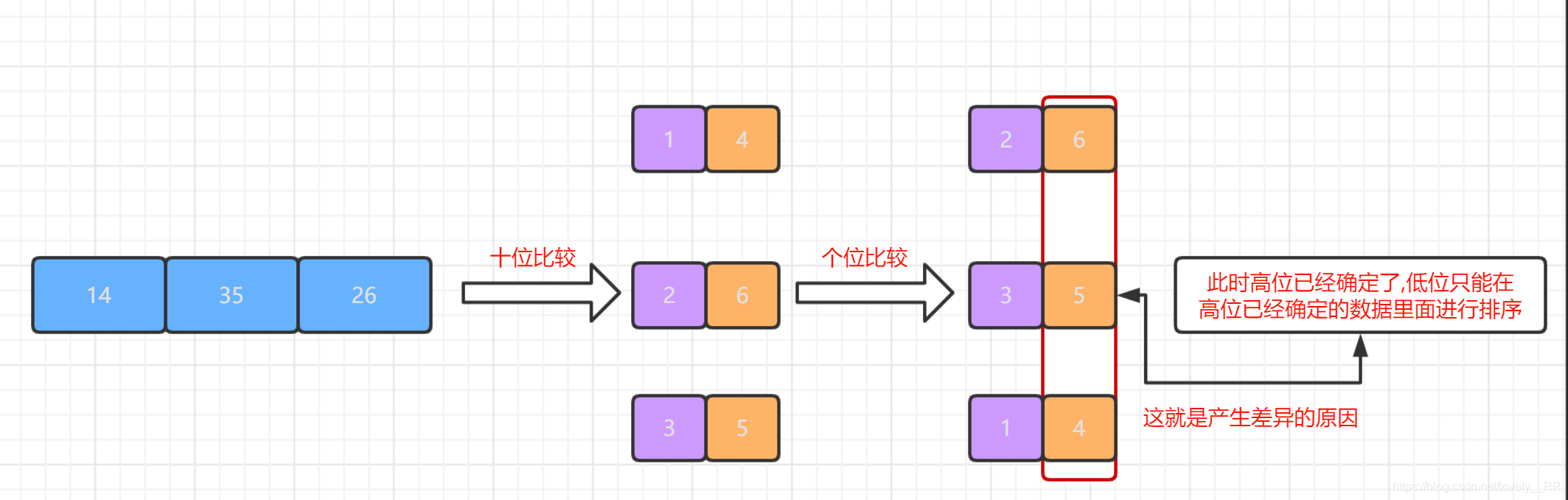
正是因为这个原因,所以我们采取的是从低位到高位比较的过程.
说完基本思想之后,我们来说一下算法的实现步骤:
-
1.我们第一次遍历序列.找出序列中的最大值MAX,找到MAX之后我们可以确定我们需要比较多少数位了.
-
2.这时候我们就需要按照元素在该位数对应的数字将元素存入到相应的容器之中.如下图所示:
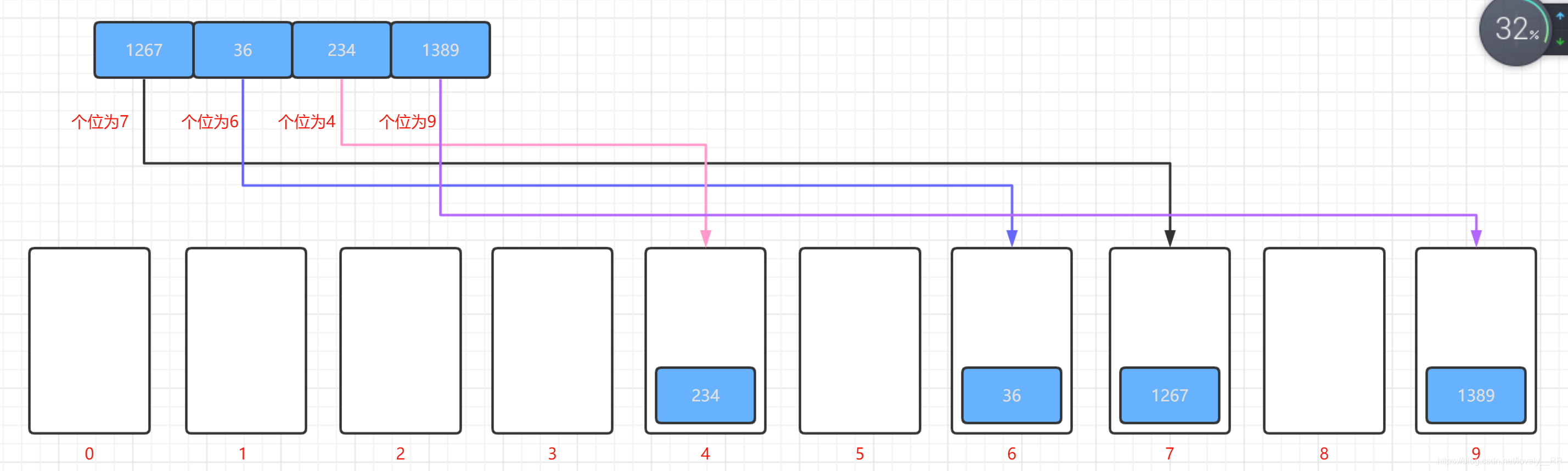
-
3.之后我们再按照容器的顺序将元素重新弹出构成我们接下来需要排序的序列,如下图所示:
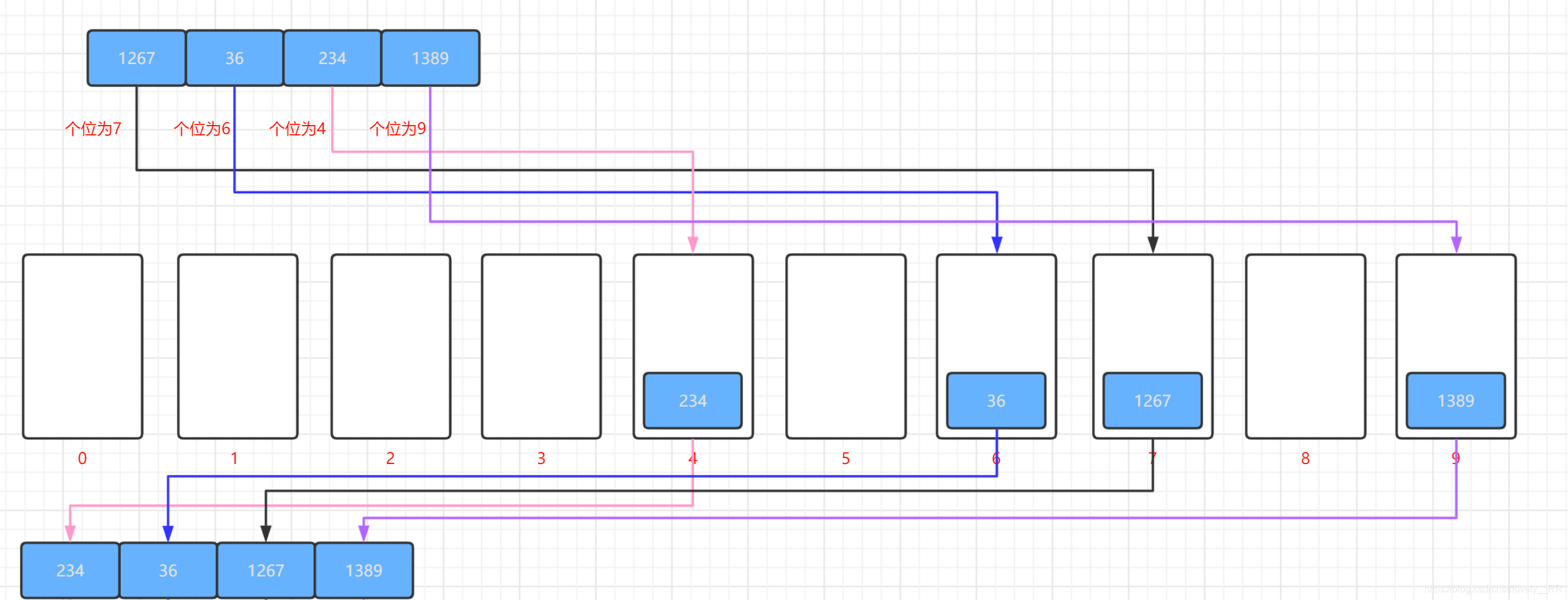
这个从容器弹出的过程需要注意一点,那就是遵循先进先出的原则,所以这个容器选择队列或者是链表比较合适,不能选择栈,因为栈是先进后出,拿取元素的时候回非常麻烦. -
4.最后只需要
重复2,3步骤,直到最高位也比较完毕,那么整个基数排序就已经完成了.
接下来我们还是通过下面的图来动态演示一下基数排序的过程:
个位排序:
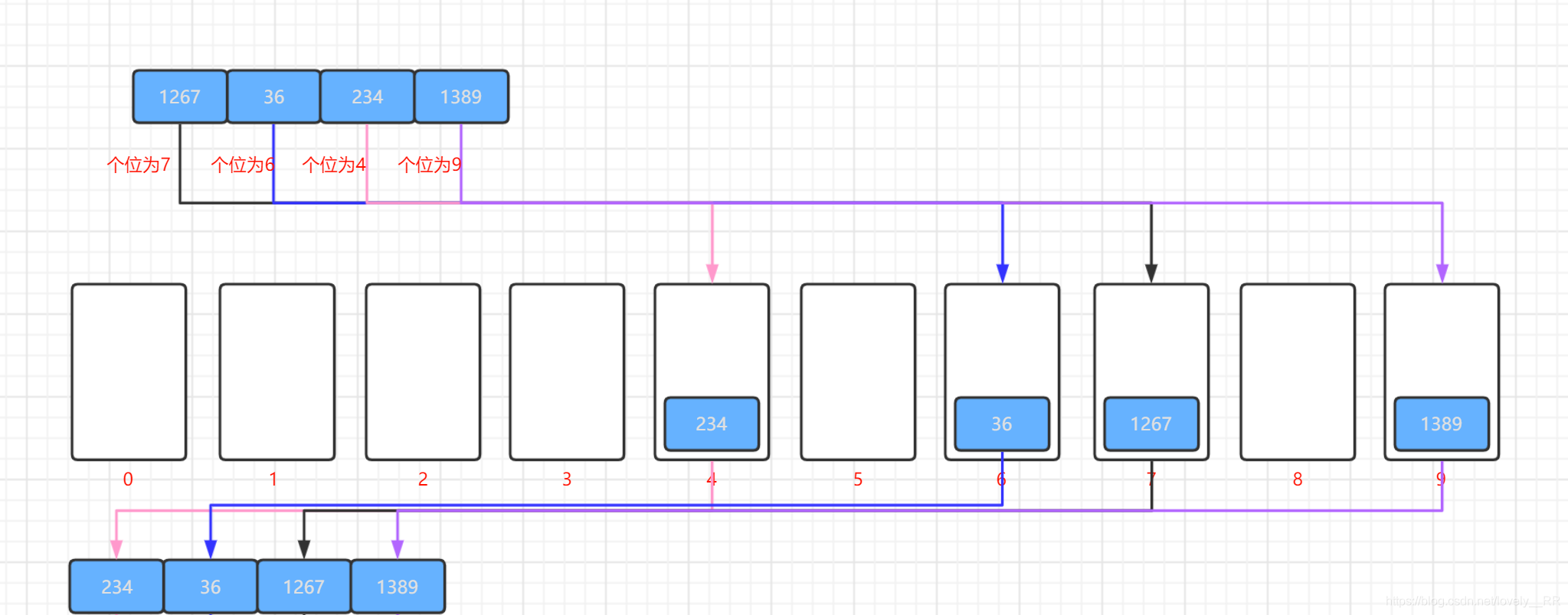
十位排序:
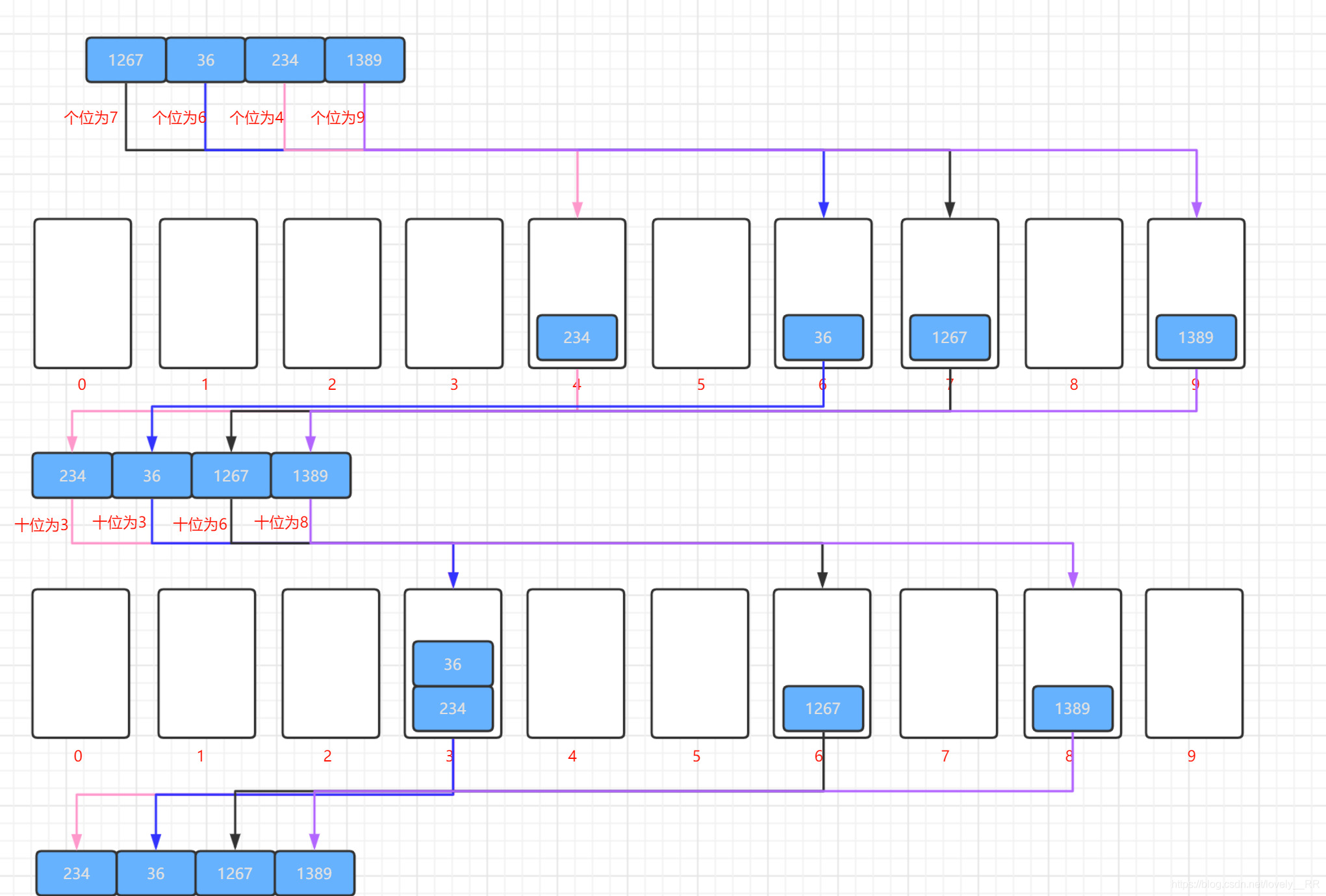
百位排序:
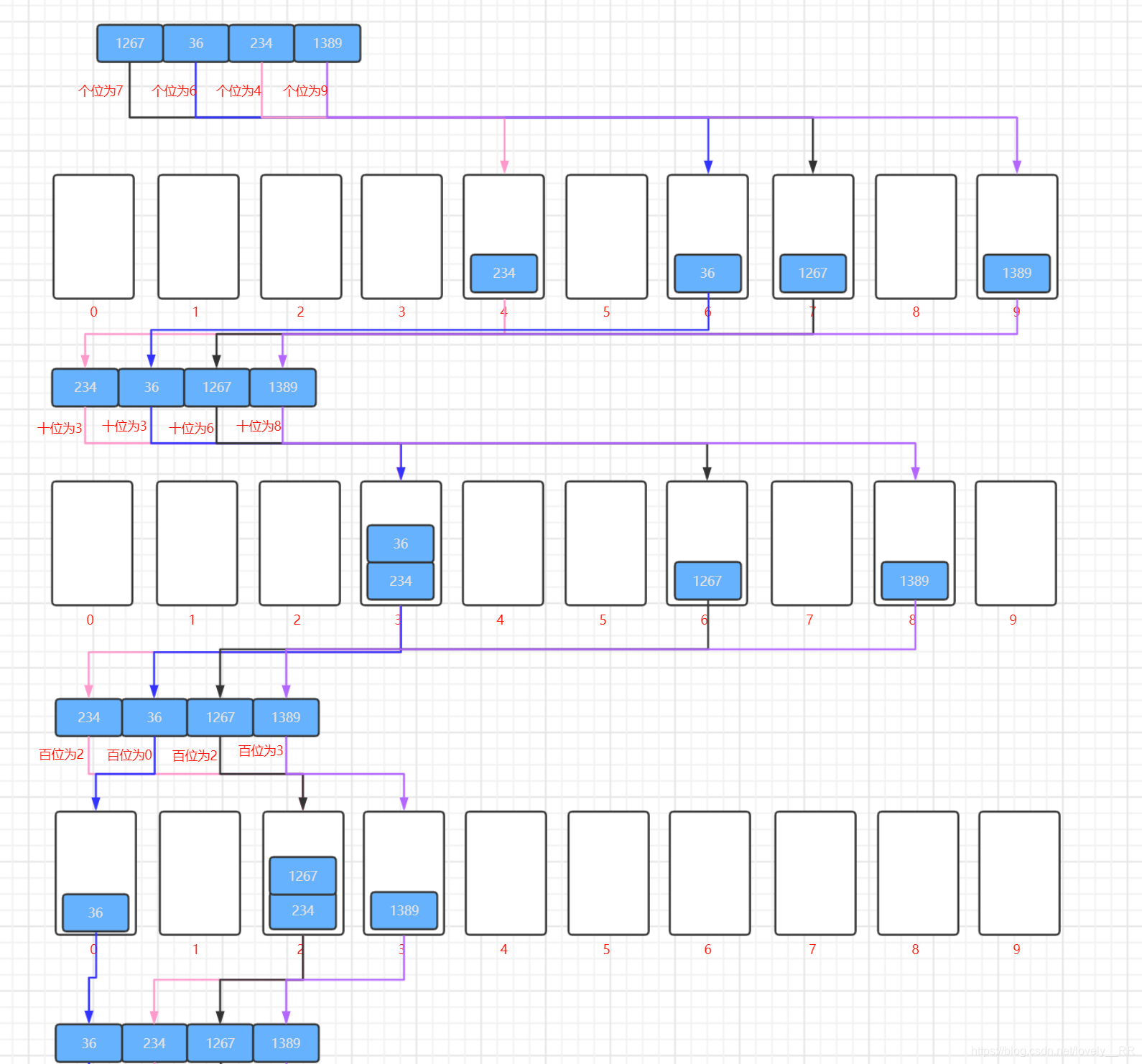
千位排序:

在了解完基数排序的基本思想之后,按照惯例我们还是来简单分析一下基数排序的特点:
- 基数排序是
稳定的,原因和桶排序以及计数排序的原因一样.
算法图解:

示例代码:
//将所有的数组合并成原来的数组 public static void merge(ArrayList<Integer> list[],int num[]) { int k=0; for(int i=0;i<list.length;i++) { if(list[i]!=null) { for(int j=0;j<list[i].size();j++) { num[k++]=list[i].get(j); System.out.print(num[k-1]+" "); } } //合并完成之后需要将链表清空,否则元素会越来越多 list[i].clear(); } System.out.println(); } //将所有的元素分散到各个链表之中 public static void split(ArrayList<Integer> list[],int num[],int k) { for(int j=0;j<num.length;j++) { list[num[j]/k%10].add(num[j]); } System.out.println("-----------------------------------------------------------------------"); System.out.println("个位开始数,第"+(String.valueOf(k).length())+"位排序结果:"); for(int j=0;j<10;j++) { System.out.println((String.valueOf(k).length())+"号位,数值为"+j+"的链表结果:"+list[j]); } } public static void main(String[] args) { ArrayList<Integer>list[]=new ArrayList [10]; for(int i=0;i<10;i++) { list[i]=new ArrayList<Integer>(); } int []num ={7,14,9,333,201,1,88,6,57,10,56,74,36,234,456}; long startTime=System.currentTimeMillis(); int max=Integer.MIN_VALUE; //第一次遍历获得序列中的最大值 for(int i=0;i<num.length;i++) { if(num[i]>max) max=num[i]; } int k=1; for(int i=0;i<String.valueOf(max).length();i++) { split(list, num, k); System.out.println("第"+(i+1)+"次排序"); merge(list, num); k=k*10; } long endTime=System.currentTimeMillis(); System.out.println("程序运行时间: "+(endTime-startTime)+"ms"); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49

复杂度分析:
理解完基数排序的基本思想之后,我们就需要来分析一下他的时间复杂度,空间复杂度.
-
时间复杂度
看完我们上面的动图演示之后我们可以看到基数排序只需要根据最大元素的位数,遍历相应次数的序列即可,所以我们可以确定基数排序的时间复杂度一定是线性级别的,但是虽然是线性级别的,但是有一个系数的,这个系数就是最大元素的位数K,所以时间复杂度应该是
O(n*k) -
空间复杂度
空间复杂度我们也可以看出来,主要就是取决于
链表的数量以及序列元素的数量,所以空间复杂度为O(n+k)
到这里十大经典排序算法详解的内容就已经全部讲解完毕了.这一次文章不管是在内容的质量上或者是在文章的排版上,都是目前工作量比较大的一期.所以如果大家觉得文章还行或者觉得文章对你有帮助的话,UP希望能关注一下我的公众号:萌萌哒的瓤瓤,或者觉得关注公众号麻烦的话,也可以给我的文章一键三连.新人UP真的很需要你的支持!!!

不点在看,你也好看!
点点在看,你更好看!



