动态规划DP之背包问题2---完全背包问题_dp完全背包

目录

DP分析：

状态转移方程：

代码：

例子：

---

        与 01背包问题 不同点在于，每种物品可以使用无限次。

有 N 种物品和一个容量是 V 的背包，每种物品都有无限件可用。

第 i 种物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。

DP分析：

        解决此类问题，需要从状态表示以及状态计算进行分析。

        状态表示：问题的某种特定情况或属性。这些状态是问题的解的一部分，它们包含了问题的关键信息，可以帮助我们描述问题的结构，并且可以通过状态之间的转移来推导出最优解。可以再细分为集合（方案），描述变量表示的是什么，属性即要取的值是最大，最小或者其他。

        状态计算（状态转移）：如下，通过  和   的状态计算  变量 和  变量的状态。

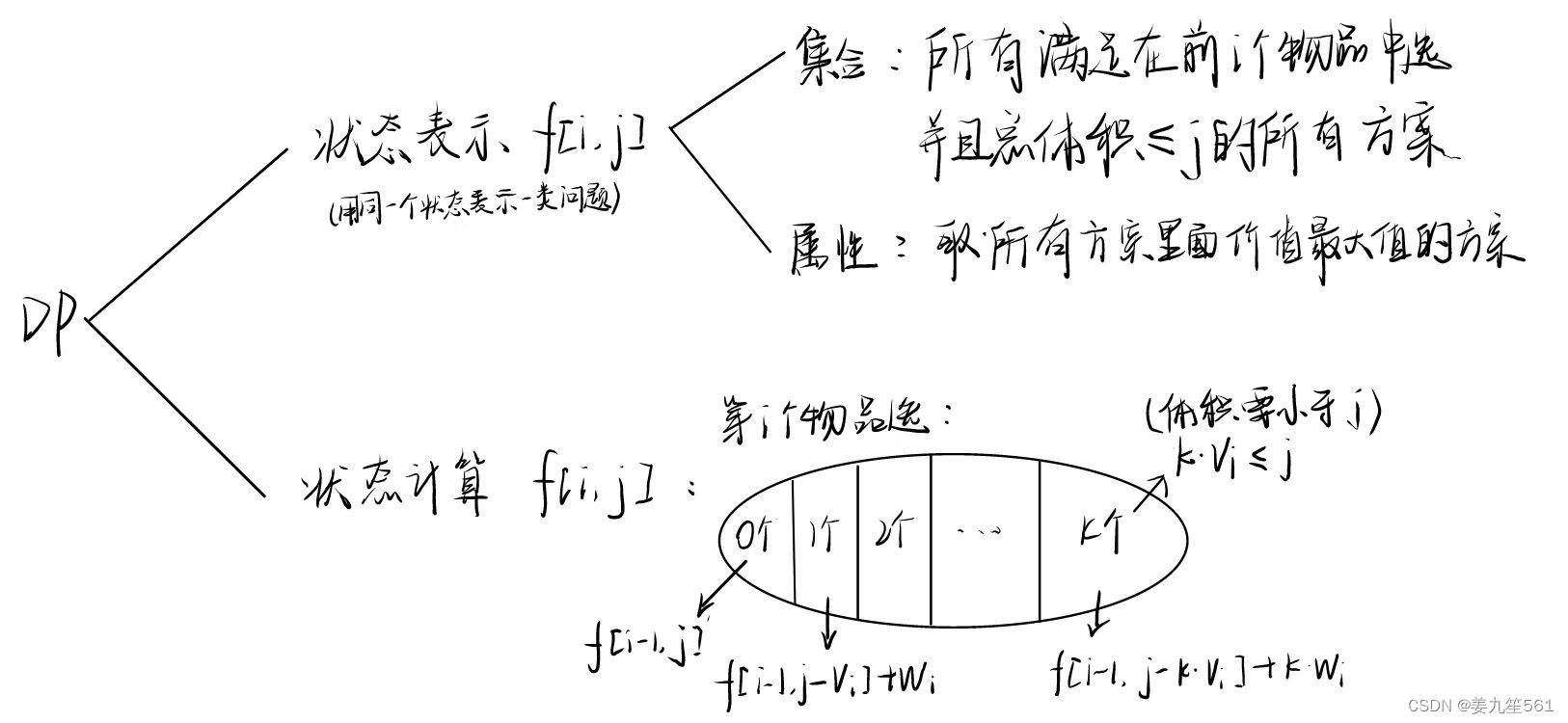
         对状态计算其中的一些分析：

​​​​​​​

     那么，最终  可以表示为：

        

        直到物品  的总体积小于         

     但是，可以发现，要对多个进行取max处理，需要多增加一层循环，时间复杂度可以达到O(n^3)，会有超时的风险。

     解决：

        

        可以发现， 可以代替  中除开  后面的所有值操作。

        即 

状态转移方程：

所以最终 的状态转移方程为：  

（很多人不理解该状态转移，理解过程如上DP分析所示，从最开始暴力解决开始分析，再依次优化，动态规划问题虽然代码看着简单，但是要理解其中原理和状态转移过程） 

        完全背包问题的状态转移方程看似和01背包问题的一样，但是其中转移过程却相隔十万八千里。动态规划DP之背包问题1---01背包问题-CSDN博客

代码：

        暴力 O(n^3)

for(int i=1;i<=n;i++){
            for(int j=0;j<=m;j++){
                f[i][j] = f[i-1][j];
                for(int k=1;k*v[i]<=j;k++)
                    if(j>=v[i]) f[i][j] = Math.max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
            }
        }

        二维优化：

for(int i=1;i<=n;i++){
    for(int j=1;j<=V;j++){ 
        f[i][j] = f[i-1][j]; // 可能一件物品都装不下
        if(j>=v[i]) // 背包体积大于物品体积
            f[i][j] = Math.max(f[i][j],f[i][j-v[i]]+w[i]); 
    }
}

         一维优化：

for(int i=1;i<=n;i++)
    for(int j=v[i];j<=V;j++)
        f[j] = Math.max(f[j],f[j-v[i]]+w[i]);

例子：

有 N 种物品和一个容量是 V 的背包，每种物品都有无限件可用。

第 i 种物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

输入格式

第一行两个整数，N，V，用空格隔开，分别表示物品种数和背包容积。

接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 种物品的体积和价值。

输出格式

输出一个整数，表示最大价值。

数据范围

0<N,V≤1000
0<vi,wi≤1000

输入样例

4 5
1 2
2 4
3 4
4 5

输出样例：

10

import java.io.*;
import java.util.*;
 
class Main{
    static int N = 1010;
    static int n,V;
    static int[] v = new int[N]; // 体积
    static int[] w = new int[N]; // 价值
    static int[] f = new int[N]; // 二维
    public static void main(String[] args) throws IOException{
        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
        String[] s = in.readLine().split(" ");
        n = Integer.parseInt(s[0]);
        V = Integer.parseInt(s[1]);
        
        for(int i=1;i<=n;i++){
            s = in.readLine().split(" ");
            v[i] = Integer.parseInt(s[0]);
            w[i] = Integer.parseInt(s[1]);
        }
        
        // 完全背包：
        for(int i=1;i<=n;i++)
            for(int j=v[i];j<=V;j++)
                f[j] = Math.max(f[j],f[j-v[i]]+w[i]);
        System.out.println(f[V]); 
    }
}