K均值聚类的失效性分析_k均值 分类失败

K均值聚类是一种应用广泛的聚类技术，特别是它不依赖于任何对数据所做的假设，比如说，给定一个数据集合及对应的类数目，就可以运用K均值方法，通过最小化均方误差，来进行聚类分析。

因此，K均值实际上是一个最优化问题。在一些已知的文献中论述了K均值聚类的一下一些缺点：

• K均值假设每个变量的分布是球形的；
• 所有的变量具有相同的方差；
• 类具有相同的先验概率，要求每个类拥有相同数量的观测；
• 上述三条任何一条不满足，K均值算法即失效了

一个典型的非球形分布如下图所示：

在这个图中，我们可以直观的看出 观测可以分成两类：中心位置的样本数据为一类、外围圆上的样本数据为一类。

使用K均值聚类的效果如下：

K均值试图最小化均方误差，并且得到了一个明显错误的聚类结果。

你可能会说，这不是一个公平的例子，没有聚类方法可以处理这么怪异的类分布。事实并非如此，single linkage hierachical clustering（层次聚类算法的一种）算法就是一个很不错的选择，下面是该算法得到的一个聚类效果：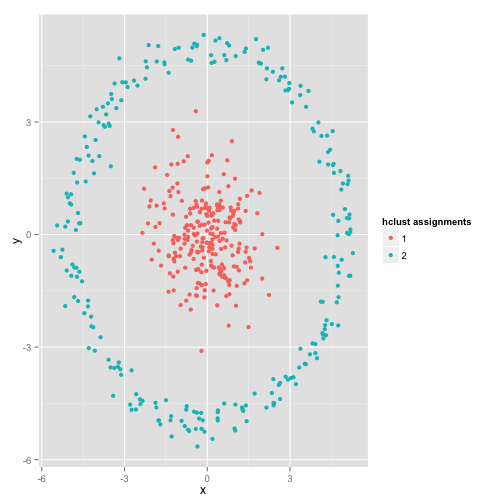

这是因为single linkage hierachical clustering算法对数据集做了正确的假设(实际上，在其他的情况下，该算法也可能会失效，同时任何算法本身就是有局限的)。

实际上，对于这类数据，K均值仍然可以正常的工作。在此，将以上数据转换成极坐标的形式，得到如下的聚类效果：

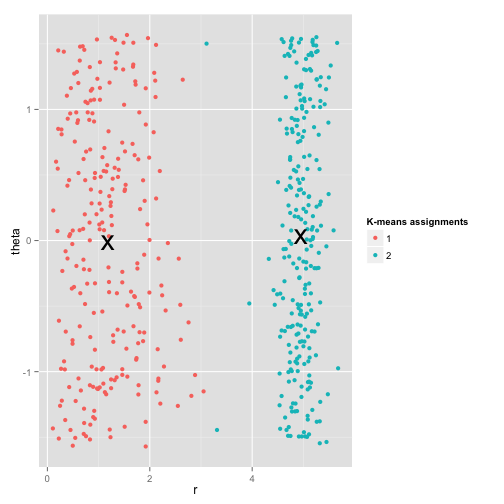因此，使用模型的时候，理解模型的过程及需要的运用条件是至关重要的。

在样本数量不均衡的情况下，K均值聚类的效果如何呢？在此，我们利用多维高斯分布生产了包含三个类的数据集，类样本的数量分别是20、100、500，如下图所示：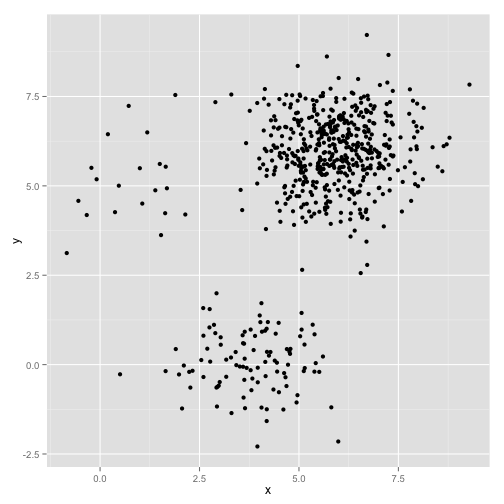

看起来K均值算法可以很好的处理这类问题，是骡子是马拉出来遛遛，使用K均值聚类效果如下：

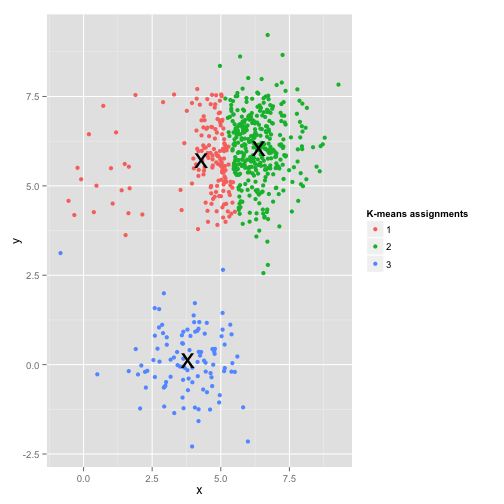在最小化均方误差的过程中，大类由于数量庞大，最终的误差基本取决于大类的误差，因此小类直接被忽视掉了。在这种情况下，小类最好的方式就是在空间上与大类保持一定的距离，聚类时，才能独立成类。否则，容易被误认为离群点进行处理。

“天下没有免费的午餐”，这句谚语在机器学习中非常受用，没有一个算法可以很好的处理所有的情况。理解每种算法，及其所需的假设，在运用具体的算法时，通过对数据的预处理有时可以将数据变换至对应的假设上，以使得算法能够正常的工作。