动态规划之状态压缩_js 若先出手的玩家是否能稳赢则返回 true ,否则返回 false 。假设两位玩家游戏时

---

464. 我能赢吗

在 “100 game” 这个游戏中，两名玩家轮流选择从 1 到 10 的任意整数，累计整数和，先使得累计整数和 达到或超过 100 的玩家，即为胜者。

如果我们将游戏规则改为 “玩家 不能 重复使用整数” 呢？

例如，两个玩家可以轮流从公共整数池中抽取从 1 到 15 的整数（不放回），直到累计整数和 >= 100。

给定两个整数 maxChoosableInteger （整数池中可选择的最大数）和 desiredTotal（累计和），若先出手的玩家是否能稳赢则返回 true ，否则返回 false 。假设两位玩家游戏时都表现 最佳 。
1 <= maxChoosableInteger <= 20
0 <= desiredTotal <= 300

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/can-i-win

一、解题思路

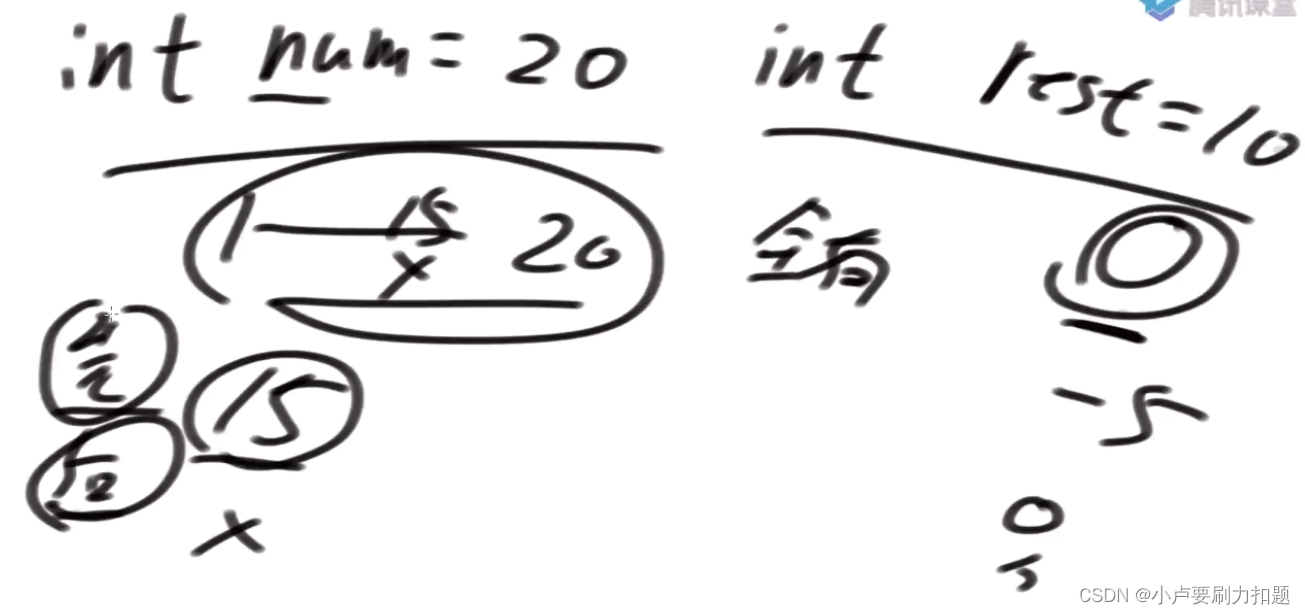
题意:你让对方最早面对一个零或负数的状态你赢。
定义f函数:你返回一个布尔类型的值,在先手和后手都绝顶聪明的情况下,先手会不会赢。如果先手会赢返回True,否则返回false,

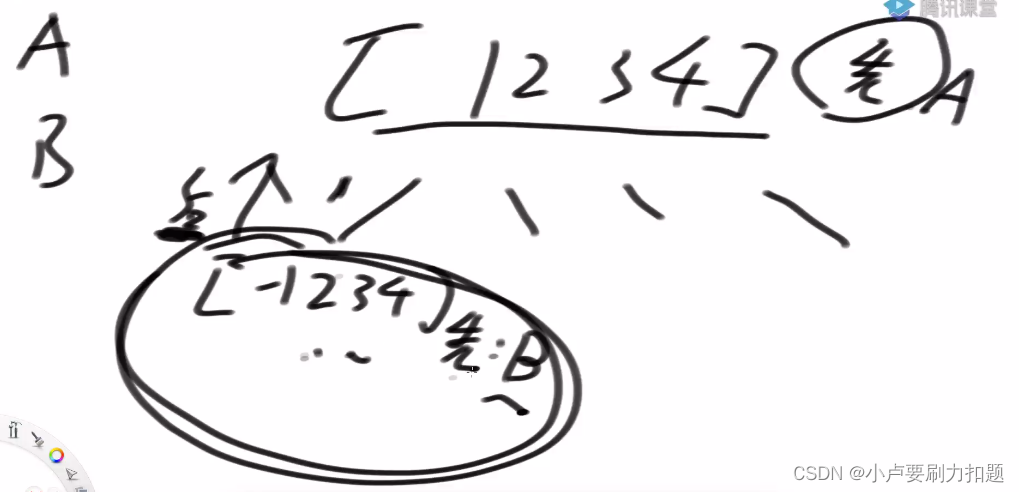
子过程的后手就是当前的先手

	// 1~choose 拥有的数字
	// total 一开始的剩余
	// 返回先手会不会赢
	public static boolean canIWin0(int choose, int total) {
		if (total == 0) {
			return true;
		}
		if ((choose * (choose + 1) >> 1) < total) {
			return false;
		}
		int[] arr = new int[choose];
		for (int i = 0; i < choose; i++) {
			arr[i] = i + 1;
		}
		// arr[i] != -1 表示arr[i]这个数字还没被拿走
		// arr[i] == -1 表示arr[i]这个数字已经被拿走
		// 集合，arr，1~choose
		return process(arr, total);
	}

	// 当前轮到先手拿，
	// 先手只能选择在arr中还存在的数字，
	// 还剩rest这么值，
	// 返回先手会不会赢
	public static boolean process(int[] arr, int rest) {
		if (rest <= 0) {
			return false;
		}
		// 先手去尝试所有的情况
		for (int i = 0; i < arr.length; i++) {
			if (arr[i] != -1) {
				int cur = arr[i];
				arr[i] = -1;
				boolean next = process(arr, rest - cur);
				arr[i] = cur;
				if (!next) {
					return true;
				}
			}
		}
		return false;
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

两个可变参数,arr可变参数的复杂程度突破了整形

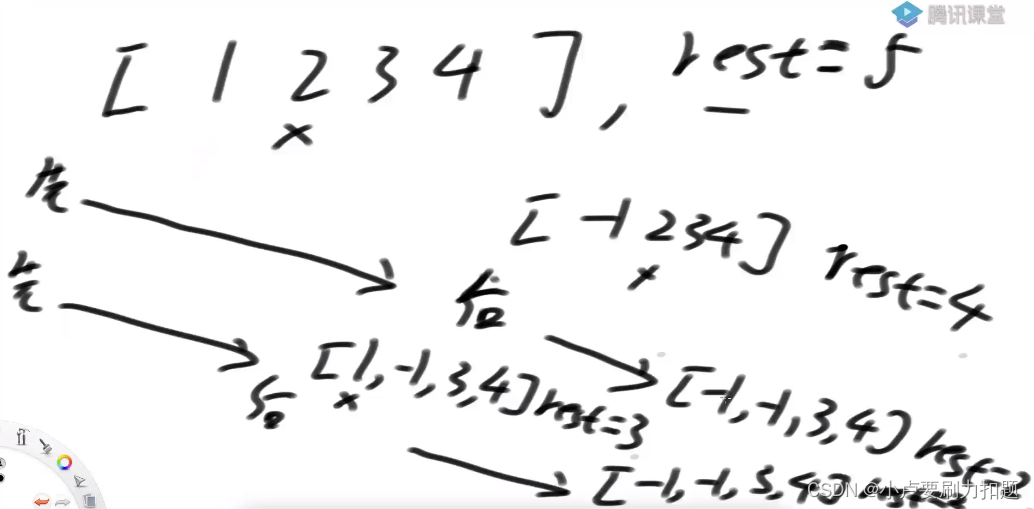
有重复过程,可以做缓存
我们说我们任何一个可变参数,你不要让它的复杂程度突破到整形以上。但是这个暴力过程f它的某一个可变参数,它是一个线性结构。
这个线性结构,它其实代表一个集合某个数字存在或不存在的这么一种状况。带着他可变参数去玩的一个尝试。但是它依然可以命中大量的重复计算。我们可变参数它只是这些数字出现的一种状态作为可变参数了,它确实比整形复杂,但是依然是有可能命中缓存的。
查看题目数字范围choose不会大于20, rest不会大于300,范围非常的窄。
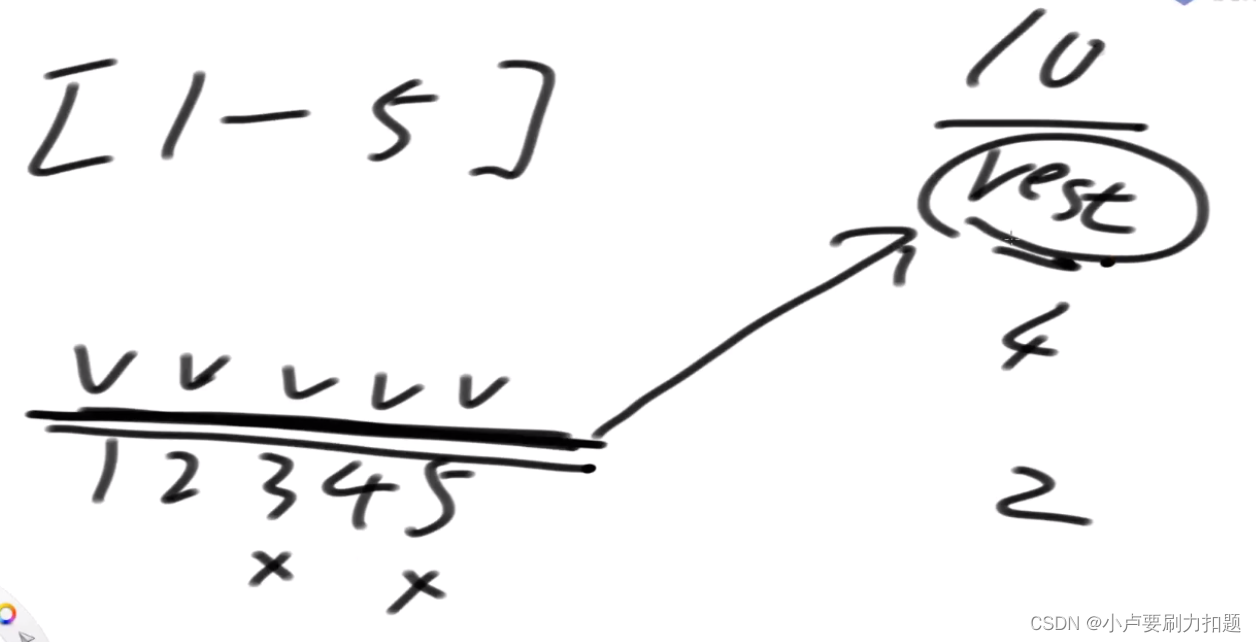
用位信息表示数字存在性

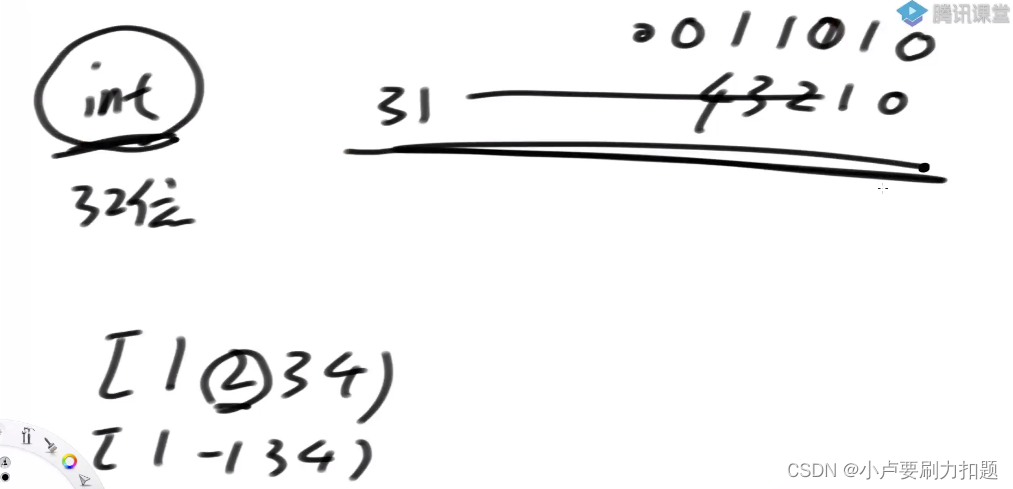
我用一个整型变量使用它的位信息。一个整型变量是有32位的,从0~31位。
所以我就可以把一个数存在不存在用位信息代替,
如果没有被拿走,那么该位为0,如果拿走了则为1

	public static boolean canIWin1(int choose, int total) {
		if (total == 0) {
			return true;
		}
		if ((choose * (choose + 1) >> 1) < total) {
			return false;
		}
		return process1(choose, 0, total);
	}

	// 当前轮到先手拿，
	// 先手可以拿1~choose中的任何一个数字
	// status   i位如果为0，代表没拿，当前可以拿
	//          i位为1，代表已经拿过了，当前不能拿
	// 还剩rest这么值，
	// 返回先手会不会赢
	public static boolean process1(int choose, int status, int rest) {
		if (rest <= 0) {
			return false;
		}
		for (int i = 1; i <= choose; i++) {
			if (((1 << i) & status) == 0) { // i 这个数字，是此时先手的决定！
				if (!process1(choose, (status | (1 << i)), rest - i)) {
					return true;
				}
			}
		}
		return false;
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

status可以决定rest,rest的状态决定不了status,它俩不独立,于是一维动态规划表就够了。

dp表变化范围,0位弃而不用,如果你有N个数。你就需要N加1位二进制位。需要准备N加1位二进制位大小的一张表

	public static boolean canIWin2(int choose, int total) {
		if (total == 0) {
			return true;
		}
		if ((choose * (choose + 1) >> 1) < total) {
			return false;
		}
		int[] dp = new int[1 << (choose + 1)];
		// dp[status] == 1  true
		// dp[status] == -1  false
		// dp[status] == 0  process(status) 没算过！去算！
		return process2(choose, 0, total, dp);
	}

	// 为什么明明status和rest是两个可变参数，却只用status来代表状态(也就是dp)
	// 因为选了一批数字之后，得到的和一定是一样的，所以rest是由status决定的，所以rest不需要参与记忆化搜索
	public static boolean process2(int choose, int status, int rest, int[] dp) {
		if (dp[status] != 0) {
			return dp[status] == 1 ? true : false;
		}
		boolean ans = false;
		if (rest > 0) {
			for (int i = 1; i <= choose; i++) {
				if (((1 << i) & status) == 0) {
					if (!process2(choose, (status | (1 << i)), rest - i, dp)) {
						ans = true;
						break;
					}
				}
			}
		}
		dp[status] = ans ? 1 : -1;
		return ans;
	}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

总结

它说明的是我一个F函数有某一个可变参数。它是一个线性结构。但它表示的状况是某个位置存在或者不存在。我可以把它转成整形,虽然转成了整形,但其实实质还是线性结构。所以在面试场上这样的题真的很少。这种类型的题目提醒你的特征是啥呢?看数据量,题目说拿的number不会突破20,所以复杂度是O(2^ 20*20)在10^ 8以内.所以你看到数据量少,一方面我们想到分治,另一方面就可能想到这玩意可能是一个状态压缩动态规划。它的设计参数的这个可变参数,它突破到了整形以上其实变成一种线性结构,虽然我可以拿整形来替代它,但它其实已经是线性的结构了。这种题出现的概率低于5%,这一类为题问题中最经典的一个就是TSP问题。

TSP问题

有N个城市，任何两个城市之间的都有距离，任何一座城市到自己的距离都为0。所有点到点的距 离都存在一个N*N的二维数组matrix里，也就是整张图由邻接矩阵表示。现要求一旅行商从k城市 出发必须经过每一个城市且只在一个城市逗留一次，最后回到出发的k城，返回总距离最短的路的 距离。参数给定一个matrix，给定k。

解题思路

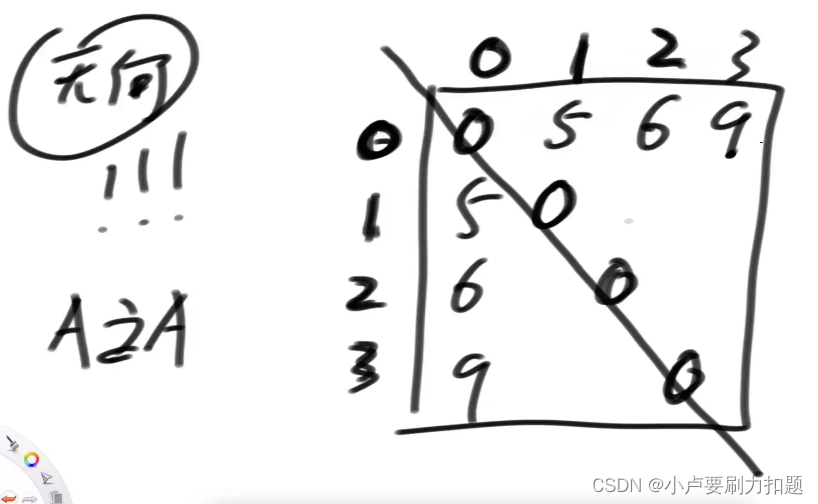
无向图,邻接矩阵中以对角线对称,自己到自己距离一定是0以这一条对角线做左右两边对称的一个矩阵从在这张表中。任何一个城市到任何一个城市都是有距离的。
问题是你怎么样选择一条路把所有城市,就比如说你选择从0出发都经过一遍,而且只经过一遍。最终回到0总距离最小。不用强调出发点,因为是一个环。
一个小人从某个点出发,比如从1出去,最后回到1,
沿途的每一个城市都必须经过一遍,而且只能经过一遍在这个过程中,我选哪条路让总距离最短
TSP问题有个特征不管从哪个城市出发最终回到哪个城市,最短的总距离是一样的因为你整个最优的路是一个环,也就是说TSP问题是不用指定从哪出发的,他不管从哪里出发,转一圆回来都是一样的,最优总距离

尝试怎么写?
假设我有一个递归函数第一个参数是一个集合
第二个参数,假设是某一个出发点,出发点一定是属于这个集合里的某个点
我有一个规定好的源出发点,一个外部信息,跟f没有关系
f函数含义:通过这个出发点把这个集合里面所有东西都联通之后,最终回到源出发点,请问最优总距离是多少?

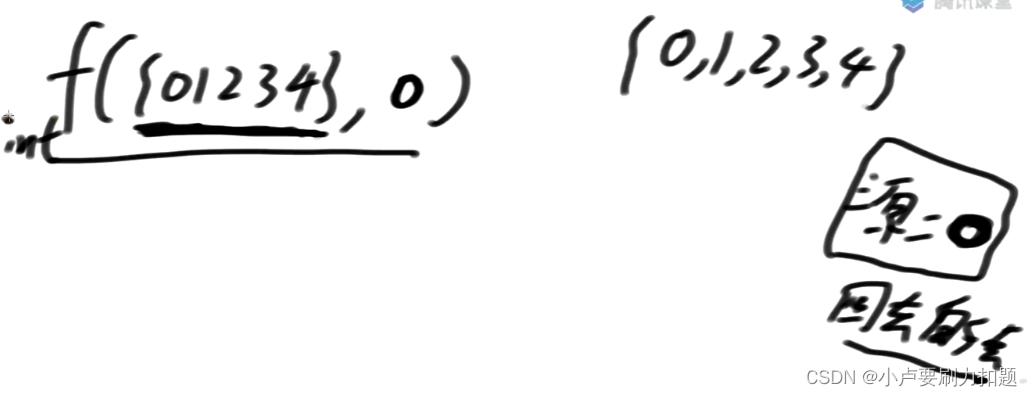
假设有5做城市0,1,2,3,4
假设源出发点就是0,最终要回去的点
主函数怎么调?f([0,1,2,3,4), 0)
集合里有0,1,2,3,4五座城,指定好了从0出发,最终把通过0,1,2,3,4城市之后再回到原来的点这个过程中最优距离是多少,请返回

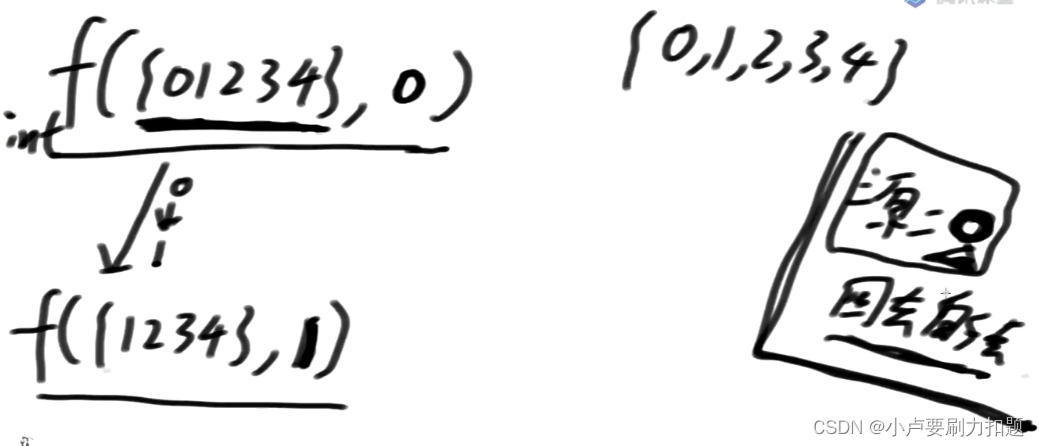
往下怎么调?现在来到0这个点,有几种选择?能怎么选?
我们可以选择从0出发到1,因此我们需要往下调f({1,2,3,4},1),
我们也可以选择从0出发到2,往下调f({1,2,3,4},2),
我们也可以选择从0出发到3,往下调f({1,2,3,4},3)
…
这些距离我求出来,最后选出最小距离

	public static int t1(int[][] matrix) {
		int N = matrix.length; // 0...N-1
		// set
		// set.get(i) != null i这座城市在集合里
		// set.get(i) == null i这座城市不在集合里
		List<Integer> set = new ArrayList<>();
		for (int i = 0; i < N; i++) {
			set.add(1);
		}
		return func1(matrix, set, 0);
	}

	// 任何两座城市之间的距离，可以在matrix里面拿到
	// set中表示着哪些城市的集合，
	// start这座城一定在set里，
	// 从start出发，要把set中所有的城市过一遍，最终回到0这座城市，最小距离是多少
	public static int func1(int[][] matrix, List<Integer> set, int start) {
		int cityNum = 0;
		for (int i = 0; i < set.size(); i++) {
			if (set.get(i) != null) {
				cityNum++;
			}
		}
		if (cityNum == 1) {
			return matrix[start][0];
		}
		// cityNum > 1  不只start这一座城
		set.set(start, null);
		int min = Integer.MAX_VALUE;
		for (int i = 0; i < set.size(); i++) {
			if (set.get(i) != null) {
				// start -> i i... -> 0
				int cur = matrix[start][i] + func1(matrix, set, i);
				min = Math.min(min, cur);
			}
		}
		set.set(start, 1);
		return min;
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

我们可以运用位运算优化,使线性结构变为整形,有多少座城就有多少个1,假设有7座城,那么状态码初始化为1111111
如果该位为0,则代表这座城已经去过

	public static int t2(int[][] matrix) {
		int N = matrix.length; // 0...N-1
		// 7座城 1111111
		int allCity = (1 << N) - 1;
		return f2(matrix, allCity, 0);
	}

	// 任何两座城市之间的距离，可以在matrix里面拿到
	// set中表示着哪些城市的集合，
	// start这座城一定在set里，
	// 从start出发，要把set中所有的城市过一遍，最终回到0这座城市，最小距离是多少
	public static int f2(int[][] matrix, int cityStatus, int start) {
		// cityStatus == cityStatux & (~cityStaus + 1)

		if (cityStatus == (cityStatus & (~cityStatus + 1))) {
			return matrix[start][0];
		}

		// 把start位的1去掉，
		cityStatus &= (~(1 << start));
		int min = Integer.MAX_VALUE;
		// 枚举所有的城市
		for (int move = 0; move < matrix.length; move++) {
			if ((cityStatus & (1 << move)) != 0) {
				int cur = matrix[start][move] + f2(matrix, cityStatus, move);
				min = Math.min(min, cur);
			}
		}
		cityStatus |= (1 << start);
		return min;
	}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

两个可变参数会不会撞到重复解?

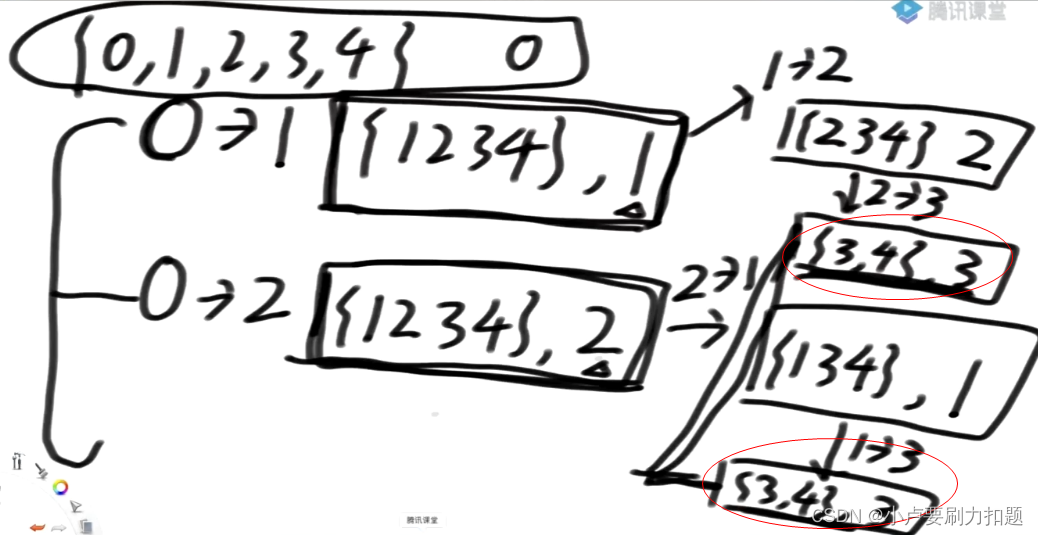
有重复解势,必存在某种形式的动态规划,不让它重复计算

	public static int t3(int[][] matrix) {
		int N = matrix.length; // 0...N-1
		// 7座城 1111111
		int allCity = (1 << N) - 1;
		int[][] dp = new int[1 << N][N];
		for (int i = 0; i < (1 << N); i++) {
			for (int j = 0; j < N; j++) {
				dp[i][j] = -1;
			}
		}
		return f3(matrix, allCity, 0, dp);
	}

	// 任何两座城市之间的距离，可以在matrix里面拿到
	// set中表示着哪些城市的集合，
	// start这座城一定在set里，
	// 从start出发，要把set中所有的城市过一遍，最终回到0这座城市，最小距离是多少
	public static int f3(int[][] matrix, int cityStatus, int start, int[][] dp) {
		if (dp[cityStatus][start] != -1) {
			return dp[cityStatus][start];
		}
		if (cityStatus == (cityStatus & (~cityStatus + 1))) {
			dp[cityStatus][start] = matrix[start][0];
		} else {
			// 把start位的1去掉，
			cityStatus &= (~(1 << start));
			int min = Integer.MAX_VALUE;
			// 枚举所有的城市
			for (int move = 0; move < matrix.length; move++) {
				if (move != start && (cityStatus & (1 << move)) != 0) {
					int cur = matrix[start][move] + f3(matrix, cityStatus, move, dp);
					min = Math.min(min, cur);
				}
			}
			cityStatus |= (1 << start);
			dp[cityStatus][start] = min;
		}
		return dp[cityStatus][start];
	}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40