08 高斯滤波

---

前言

之前在07 Canny算子中，第一步就要进行高斯滤波的操作，本文实现手写一个函数完成高斯滤波的功能。

---

一、高斯滤波是什么？

高斯滤波是一种线性平滑滤波，适用于消除高斯噪声，广泛应用于图像处理的减噪过程。

通俗的讲，高斯滤波就是对整幅图像进行加权平均的过程，每一个像素点的值，都由其本身和邻域内的其他像素值经过加权平均后得到。高斯滤波的具体操作是：用一个模板（或称卷积、掩模）扫描图像中的每一个像素，用模板确定的邻域内像素的加权平均灰度值去替代模板中心像素点的值。
只不过这个模板是服从高斯分布的。

二、理论储备

1.一维高斯

一维高斯函数的构造如下：

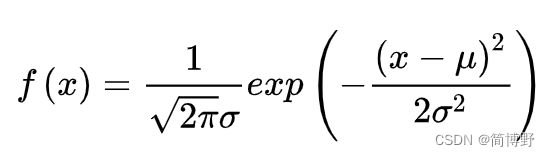
代码如下（示例）：

import numpy as np
import matplotlib.pyplot as plt
mu=0        #均值
#sigma=0.2   #标准差
x=np.linspace(-3,3,60)
for i in range(2,10,2):
    sigma = i/10
    y=np.exp((-(x-mu)**2)/(2*(sigma**2)))/(np.sqrt(2*np.pi)*sigma)
    plt.plot(x,y,"b-",)
plt.grid(True)
plt.show()
1
2
3
4
5
6
7
8
9
10
11

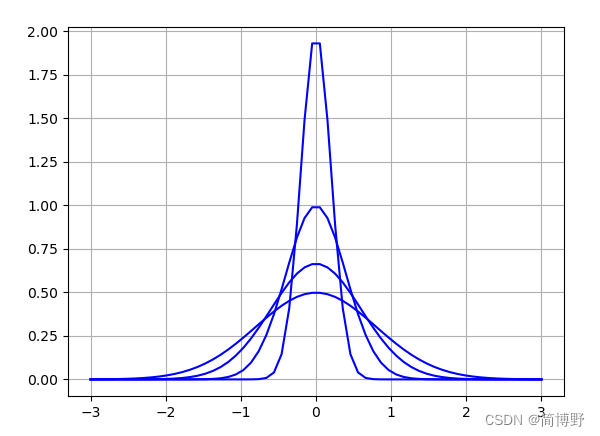
上图为只改变sigma的一维高斯函数。但是看上去很乱，而且也不知道相应的sigma。

import numpy as np
import matplotlib.pyplot as plt
mu=0        #均值
#sigma=0.2   #标准差
x=np.linspace(-3,3,60)
colors = ['b', 'g', 'r', 'c', 'm']  # 定义不同颜色
for i in range(2,10,2):
    sigma = i/10
    y=np.exp((-(x-mu)**2)/(2*(sigma**2)))/(np.sqrt(2*np.pi)*sigma)
    plt.plot(x,y,color=colors[(i//2)-1], label='sigma={}'.format(sigma))
plt.grid(True)
plt.legend()  # 显示图例
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13

因此，将上面代码进行修改如下：

2.二维高斯函数

由于图像是二维的，一维高斯函数肯定是不能满足我们的需求的。其中x表示邻域像素距离中心点水平方向的间距，y表示垂直方向的间距：

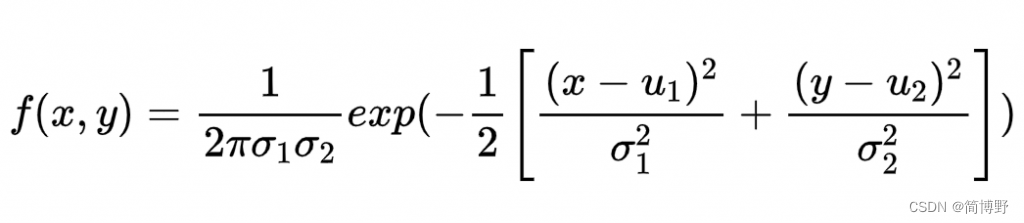
代码如下（示例）：

import numpy as np
import matplotlib.pyplot as plt
def two_dim_gaussian(x, y, sigma_x, sigma_y, x0, y0):
    Z = np.exp((-0.5)*((x-x0)**2/(sigma_x)**2 +(y-y0)**2/(sigma_y)**2))/(np.pi*2*sigma_y*sigma_x)
    return Z
X = np.arange(-3, 3.1, 0.1,dtype=np.float64).reshape(-1,1)
Y = np.arange(-3, 3.1, 0.1,dtype=np.float64)
mux,muy=0,0
sigmax,sigmay = 0.8,0.8
Z = two_dim_gaussian(X,Y,sigmax,sigmay,mux,muy)
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.plot_surface(X, Y, Z, cmap='coolwarm')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

3生成高斯卷积核

import numpy as np
import matplotlib.pyplot as plt
def two_dim_gaussian(x, y, sigma_x, sigma_y, x0, y0):
    Z = np.exp((-0.5)*((x-x0)**2/(sigma_x)**2 +(y-y0)**2/(sigma_y)**2))/(np.pi*2*sigma_y*sigma_x)
    return Z
X = np.arange(-2, 3, 1,dtype=np.float64).reshape(-1,1)
Y = np.arange(-2, 3, 1,dtype=np.float64)
mux,muy=0,0
sigmax,sigmay = 0.8,0.8
Z = two_dim_gaussian(X,Y,sigmax,sigmay,mux,muy)
print(Z)
1
2
3
4
5
6
7
8
9
10
11

生成5*5卷积核：

对这部分进行归一化得到：

---