数据结构（树）

数据结构（树）

        度：每一个节点的子节点数量

 二叉查找树：

          每一个节点上最多有两个子节点；

         任意节点左子树上的值都小于当前节点；

         任意节点右子树上的值都大于当前节点。

        添加节点规则：

        小的存左边，大的存右边，一样的不存

        查找规则：和添加一样

        弊端：

        当数据有序时，插入效率低

二叉树的遍历方式：

        前序遍历：

        从根节点开始，然后按照当前结点，左子结点，右子结点的顺序遍历

        中序遍历：

        从最左边的子节点开始，然后按照左子结点，当前结点，右子结点的顺序遍历

        后序遍历：

        从最左边的子节点开始，然后按照左子结点，右子结点，当前结点的顺序遍历

        层序遍历：

        从根节点开始一层一层的遍历

平衡二叉树：

        规则：

        任意节点左右子树高度差不超过1

        平衡机制：

         规则1：左旋

        确定支点：从添加的结点开始，不断往父节点找不平衡的节点

        步骤： 1） 把不平衡的点作为支点，把支点左旋降级，变成左子结点，晋升原来的右子节点

        把不平衡的点作为支点；将根节点的右侧往左拉；原先的右子节点变成新的父节点，并把多余的左子节点出让，给已经降级的根节点当右节点

         规则2：右旋

         确定支点：从添加的结点开始，不断往父节点找不平衡的节点

        步骤： 1） 把不平衡的点作为支点，把支点右旋降级，变成右子结点，晋升原来的左子节点

         把不平衡的点作为支点；将根节点的左侧往右拉；原先的左子节点变成新的父节点，并把多余的右子节点出让，给已经降级的根节点当左子节点

         触发时机：当添加一个节点之后，该树不再是一颗平衡二叉树

需要旋转的四种情况：

        左左：

        当根节点左子树的左子树有节点插入，导致二叉树不平衡

        需要一次右旋

        左右：

        当根节点左子树的右子树有节点插入，导致二叉树不平衡

        先局部左旋，到左左情况，然后再整体右旋

        右右：

         当根节点右子树的右子树有节点插入，导致二叉树不平衡

        需要一次左旋

        右左：

        当根节点右子树的左子树有节点插入，导致二叉树不平衡

        先局部右旋，到右右情况，然后再整体左旋

红黑树：

        红黑树是一种自平衡的二叉查找树，每个节点上都有存储位表示节点的颜色；

        每一个节点可以是红或者黑；

        红黑树不是高度平衡的，它的平衡是通过“红黑规则”进行实现的

        红黑规则：

        每一个节点是红色或是黑色；

        根节点必须是黑色；

        如果一个节点没有子节点或者父节点，则该节点相应的指针属性值为Nil，这些Nil视为叶节点，每个叶节点（Nil）是黑色的；

        如果某一个节点是红色，那么它的子节点必须是黑色（不能出现两个红色节点相连的情况）；

        对每一个节点，从该节点到其所有后代叶节点的简单路径上，均包含相同数目的黑色节点

        

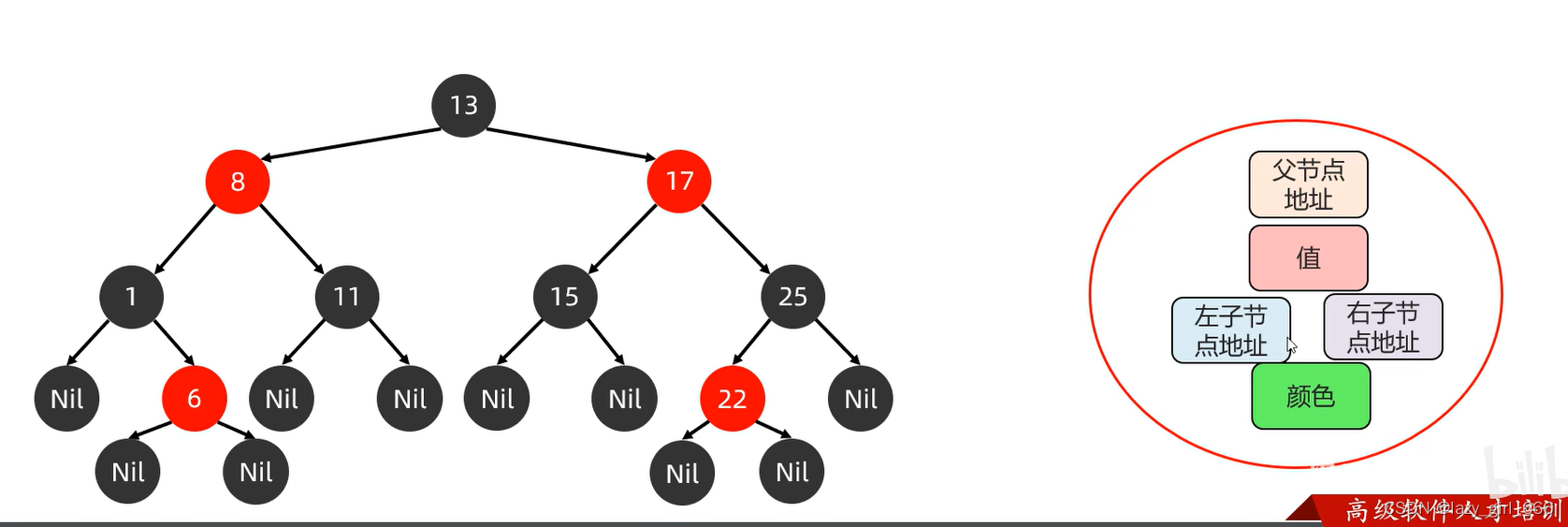
        图来自黑马程序员网课 

        添加节点规则：

        默认颜色：红色（效率高）

        

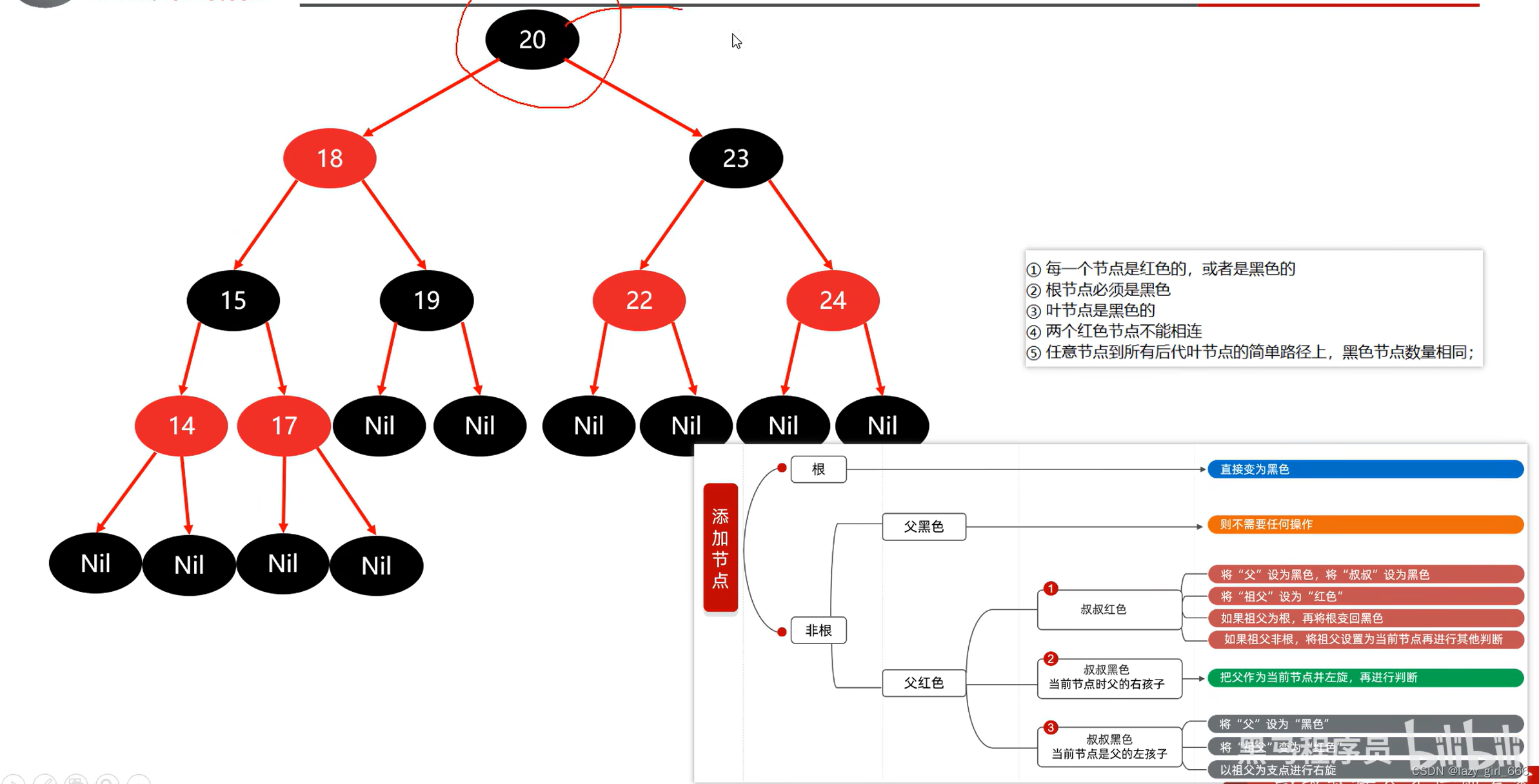
                图来自黑马程序员 

        

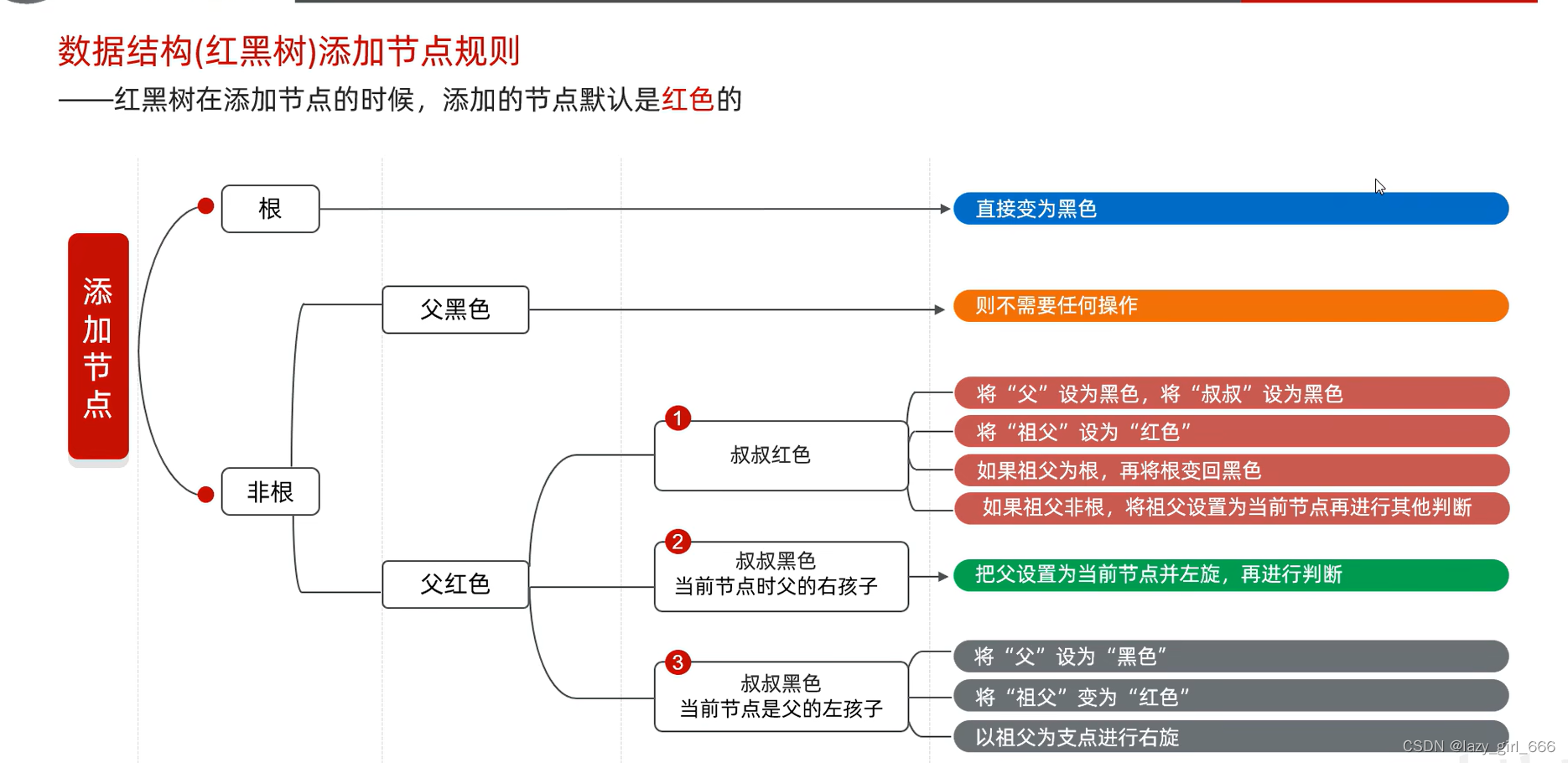
                                图来自黑马程序员 

        红黑树增删改查性能较好