（数据结构）有向图的拓扑排序 Kahn算法

拓扑排序是对有向无圈图的顶点的一种排序，使得如果存在一条从vi到vj的路径，那么在排序中，vi必须出现在vj的前面。

首先，我们需要准备一个vector<int> link[maxn]，link[i] 存放顶点i所有连接到的顶点，同时还要维护一个队列或者栈来存放所有入度为0的顶点。

下面，直接上图：

假如有这样一个有向图：

1. 我们发现只有顶点1的入度为0，所以把顶点1给去掉，并把1加入结果数组。res=[1]
   
2. 目前就还剩顶点2和顶点5的入度为0，随机去掉一个，我们去掉2，并把2加入res数组res=[1,2]

3. 目前顶点5的入度为0，把顶点5给去掉。res=[1,2,5]

4. 目前顶点4的入度为0，把顶点4给去掉。res=[1,2,5,4]

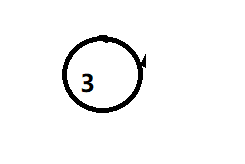
5. 目前顶点3的入度为0，把顶点3给去掉。res=[1,2,5,4,3]

直到最后不剩下顶点时，排序结束，1 2 5 4 3即为该图的一个拓扑排序。

细节：

1. 拓扑排序的结果并不唯一，比如在上面第二步，我们先去掉的是顶点2，如果我们先去掉的是顶点5，那么拓扑排序的结果可能是1 5 4 3 2
2. 假如图中有环，比如下图，那么所有的顶点的入度都不为0，排序无法进行下去，拓扑排序将不存在。所以可以通过拓扑排序来判断图中有没有环。
   

代码如下：

// Kahn算法

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define maxn 1024
vector<int> link[maxn];   //顶点i的邻接表
queue<int> q;  //存放所有入度为0的顶点
int in[maxn];   //顶点i的入度
int n;  //顶点个数
int m;  //边的个数
int res[maxn];   //存放排序后的结果

/*
新增一条由n1指向n2的有向边
*/
void lnk(int n1,int n2){
    link[n1].push_back(n2);   //n1顶点的邻接表加入n2
    ++in[n2];                 //n2的入度+1
}

int main() {
	ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    //建图
	n = 13;
    m = 15;
    lnk(1,2);
    lnk(1,6);
    lnk(1,7);
    lnk(3,1);
    lnk(3,4);
    lnk(4,6);
    lnk(6,5);
    lnk(7,4);
    lnk(7,10);
    lnk(8,7);
    lnk(9,8);
    lnk(10,11);
    lnk(10,12);
    lnk(10,13);
    lnk(12,13);
    //扫描in数组，将入度为0的顶点加入队列
    for(int i = 1;i <= n;++i){
        if(!in[i]){
            q.push(i);
        }
    }

    int index = 0;   //res的下标
    while(!q.empty()){
        int node = q.front();
        q.pop();    //拿出一个结点
        res[index++] = node; //存入结果数组
        //逐一移除跟它相连的边
        for(auto it = link[node].begin();it != link[node].end();++it){
            --in[*it];   //顶点入度-1
            if(!in[*it]){
                //如果入度为0，加入队列
                q.push(*it);
            }
        }
    }
    //如果index<n，那么加入结果数组的顶点数量一定是小于n的
    //说明该图有环
    if(index == n){
        for(int i = 0;i<n;++i){
            cout << res[i] << " \n"[i == n-1];
        }
    }else{
        cout << "circulation" << endl;
    }

	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74

练习：LeetCode No207. 课程表