排序——快速排序

目录

快速排序

快排过程文字讲解：（都以升序为最终结果）

快排步骤

快排代码部分

三数取中代码：

快排细节问题：

快排优化：小区间优化（release下没有用）

快排单趟排序的不同写法

挖坑法

双指针法

双指针文件讲解：

双指针流程图：

双指针代码实现

快排非递归实现

快排非递归代码：

---

快速排序

快排过程文字讲解：（都以升序为最终结果）

        快排又被称为霍尔排序（huoer发明的），类似于二叉树的前序遍历（根->左->右）。设置数组首的元素是keyi，快排的每次排序就相当于给keyi位置的数，找到它完成排序后应该在的位置，然后递归左右区间，给每个数都找到对应的位置。注意：在有序情况下快排会很慢。

        时间复杂度O(N*logN)；空间复杂度为O(logN)；由于快排本质类似于二叉树的前序遍历，会将数组不断地拆分递归，如果两个相同大小的数字，有一个被选中了当keyi，那么他最后会在另一个相同数字的前面还是后面呢？这也是无法控制的（两个相同的数字的相对位置就会发生改变），所以快排是不稳定排序。

快排步骤

        先三数取中，三数分别为首尾中，找到一个三个数之间的中间值，与数组首元素交换，再把首元素设置为keyi，左边从首元素开始找，右边从最末尾开始找。若不加三数取中，那么当快排遇到了本就有序的数据，耗时会更多，时间复杂度就变为了O(N^2)，很不划算，所以一定要有三数取中。

        先从最右边往左找比keyi小的元素，若找到，再从左边找比keyi大的元素，找到，交换二者的值。如果左边没有找打大的元素，直到left=right，循环也要停止。循环结束后把keyi元素和找到的值进行交换，这样就把keyi的元素放到了正确的位置。（注意：keyi设在最左边，右边先走；keyi设在最右边，左边先走）

        接着要先给keyi的位置改变，改变为left和right二者相遇的位置，递归keyi位置的左右两边区间，把数组分为三分 (begin,keyi-1)   keyi   (keyi+1,end)，函数递归结束条件设置为begin>=end，若begin=left，就说明递归到了只剩一个元素的一边；若begin>end，就说明递归到了没有元素的那边。这俩种情况，循环都要终止。

快排代码部分

//霍尔版本方法（容易出错）
void QuickSort(int *arr, int begin, int end)
{
	//递归结束条件
	//若begin=left，就说明递归到了只剩一个元素
	//若begin>end，就说明递归的没有元素的那边
	if (begin >= end)
		return;
 
	取三数，找中间值,并与beign交换（因为begin当前递归中的首元素）
	int media = Media(arr,begin,end);
	swap(&arr[begin], &arr[media]);
 
	//left和right从两端开始
	int left = begin;
	int right = end;
	int keyi = left;//把keyi位置设至当前首元素位置，对应我们后续找值
 
	//直到left和right相遇才退出循环
	while (left < right)
	{
		//先右边找小（等于循环也要继续找）
		while (left<right && arr[right] >= arr[keyi])
		{
			right--;
		}
		
		//左边找大
		while (left < right && arr[left] <= arr[keyi])
		{
			left++;
		}
		//找到交换二者的值
		swap(&arr[left], &arr[right]);
	}
 
	//交换keyi位置和相遇位置的值
	//这里right和left都行，因为只有left和right相等，代码才能走到这里
	swap(&arr[keyi], &arr[left]);
	keyi = left;//把keyi位置换到相遇的位置，方便后面进行左右递归
 
	//把数组分为三分 (begin,keyi-1)   keyi   (keyi+1,end)
	QuickSort(arr, begin, keyi - 1);
	QuickSort(arr, keyi+1, end);
}

三数取中代码：

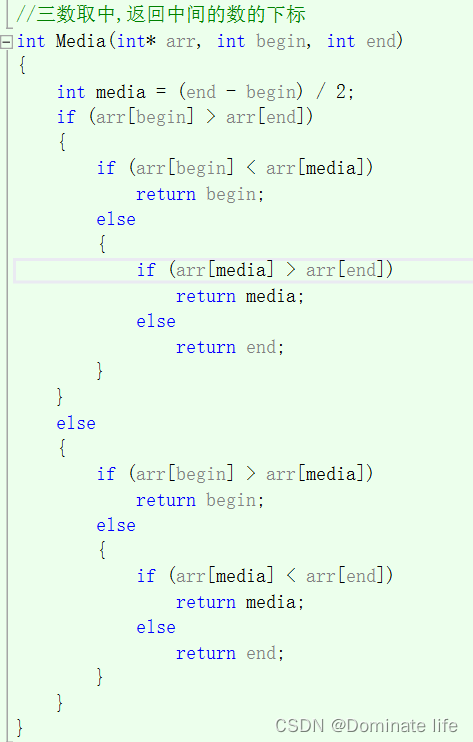
//三数取中,返回中间的数的下标
int Media(int* arr, int begin, int end)
{
	int media = (end - begin) / 2;
	if (arr[begin] > arr[end])
	{
		if (arr[begin] < arr[media])
			return begin;
		else
		{
			if (arr[media] > arr[end])
				return media;
			else
				return end;
		}
	}
	else
	{
		if (arr[begin] > arr[media])
			return begin;
		else
		{
			if (arr[media] < arr[end])
				return media;
			else
				return end;
		}
	}
}

快排细节问题：

        问题：若keyi=begin，且排升序，为什么相遇的值一定比keyi位置的值小？

        因为我们先从右边找小与keyi位置的值。分析R和L相遇只有两种情况：

        情况一：R遇L，R一直没有找到比keyi位置还小的值，直到碰到了L，跳出循环，交换L和keyi的值，由于L也是从begin位置开始的，所以这样就相当于没有交换任何数据。

        情况二：R找到了，L向右找，但没找到比keyi位置还大的值，碰到了R，退出循环，交换R和keyi位置的值，这样还是能够确保交换后keyi位置左边的数据比keyi小，右边的数据比keyi大，keyi位置的数据就相当于呆在了排序后会在的位置。

快排优化：小区间优化（release下没有用）

        在debug版本下，函数递归过深可能会导致栈溢出，系统运行也会比较慢。因为快排类似于二叉树前序遍历，而我们又知道，最后一层的二叉树的节点个数大约占整个数节点的50%。如果正常递归，后面对小区间递归时会很浪费空间和时间，所以我们当我们递归到接近最下面两层数据时，就可以用直接插入排序，从而减少最后两层原本的需要进行的大量的小递归，时间复杂度就会降低（由于release版本下对递归的空间使用优化太好了，节约了多少时间几乎看不出来，有时候可能还会导致更慢）具体代码如下：

        注意：设置的小区间不能过大，过大会导致因为过大的插入排序而造成耗时更久。

快排单趟排序的不同写法

        由于霍尔版本的单趟排序代码容易写错，所以有其他两种方法来优化单趟排序（时间复杂度没有变化）。快排函数递归部分不变，但是把单趟排序拆分出来用其他方法来写，这些函数进行单趟排序，然后返回当前数组范围内begin位置的数的正确放置位置。两种方法分别为：挖坑法和双指针法。下图为快排整体代码，挖坑法和双指针法只改变和返回keyi的位置。

//快排整体代码
void QuickSort1(int *arr, int begin, int end)
{
	//递归结束条件
	//若begin=left，就说明递归到了只剩一个元素
	//若begin>end，就说明递归的没有元素的那边
	if (begin >= end)
		return;
 
	取三数，找中间值,并与beign交换（因为begin当前递归中的首元素）
	int media = Media(arr, begin, end);
	swap(&arr[begin], &arr[media]);
 
	//使用挖坑法
	//DigHole会返回坑位的位置，这个位置就是上述begin的正确位置
	//int keyi = DigHole(arr,begin,end);
 
	//使用双指针法
	//DoublePointer会返回坑位的位置，这个位置就是上述begin的正确位置
	int keyi = DoublePointer(arr, begin, end);
 
	//把数组分为三分 (begin,keyi-1)   keyi   (keyi+1,end)
	QuickSort1(arr, begin, keyi - 1);
	QuickSort1(arr, keyi + 1, end);
}

挖坑法

        默认begin位置为坑位，把begin位置的数先额外存储在key中，方便后面覆盖。然后先从右边找到比key更小的数，将其填入坑中，再把他的位置设为坑，再从左边找比key更大的数，存入刚才重新设置的坑中，左右不断重复挖坑填坑，直到begin和end相遇，就说明相遇位置左边的数比key小，右边的数比key大，最后在把key存入相遇的坑中，就实现课单趟的排序。但最后函数要返回单趟排序后，key的位置，用于QuickSort函数递归划分区域。

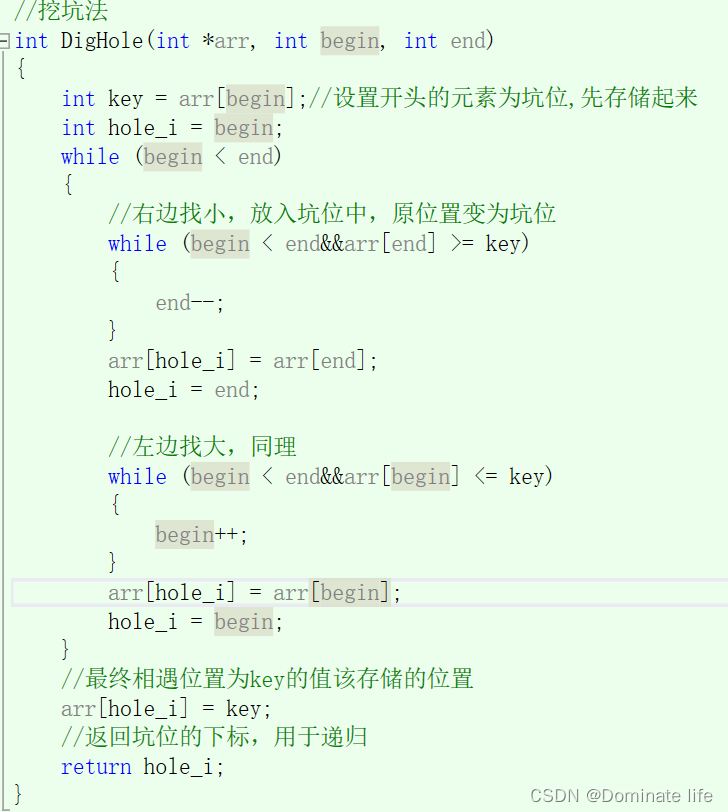
//挖坑法
int DigHole(int *arr, int begin, int end)
{
	int key = arr[begin];//设置开头的元素为坑位,先存储起来
	int hole_i = begin;
	while (begin < end)
	{
		//右边找小，放入坑位中，原位置变为坑位
		while (begin < end&&arr[end] >= key)
		{
			end--;
		}
		arr[hole_i] = arr[end];
		hole_i = end;
 
		//左边找大，同理
		while (begin < end&&arr[begin] <= key)
		{
			begin++;
		}
		arr[hole_i] = arr[begin];
		hole_i = begin;
	}
	//最终相遇位置为key的值该存储的位置
	arr[hole_i] = key;
	//返回坑位的下标，用于递归
	return hole_i;
}

双指针法

双指针文件讲解：

        用cur和prev表示快慢指针，keyi还是设为最左边，arr[keyi]就是我们需要调整的数。Prev从begin开始走，cur从begin+1开始走，一前一后。如果arr[cur]<arr[keyi]，即遇到小于keyi位置的数，prev++，再把cur位置的值与prev位置的值进行互换；如果arr[cur]>=arr[keyi]，就只进行cur++，继续往后找小。

        前后快慢指针的方法目的就是不断地把大于keyi位置的数往后移动，遇到小的就与前面的prev位置的数交换，从而确保prev和prev之前的数据一定比keyi位置的数小。这样直到cur走到end之后的位置之后，prev和cur之间的数就是大于keyi位置的数，最后交换prev和keyi位置的数就完成了一次单趟的排序。

双指针流程图：

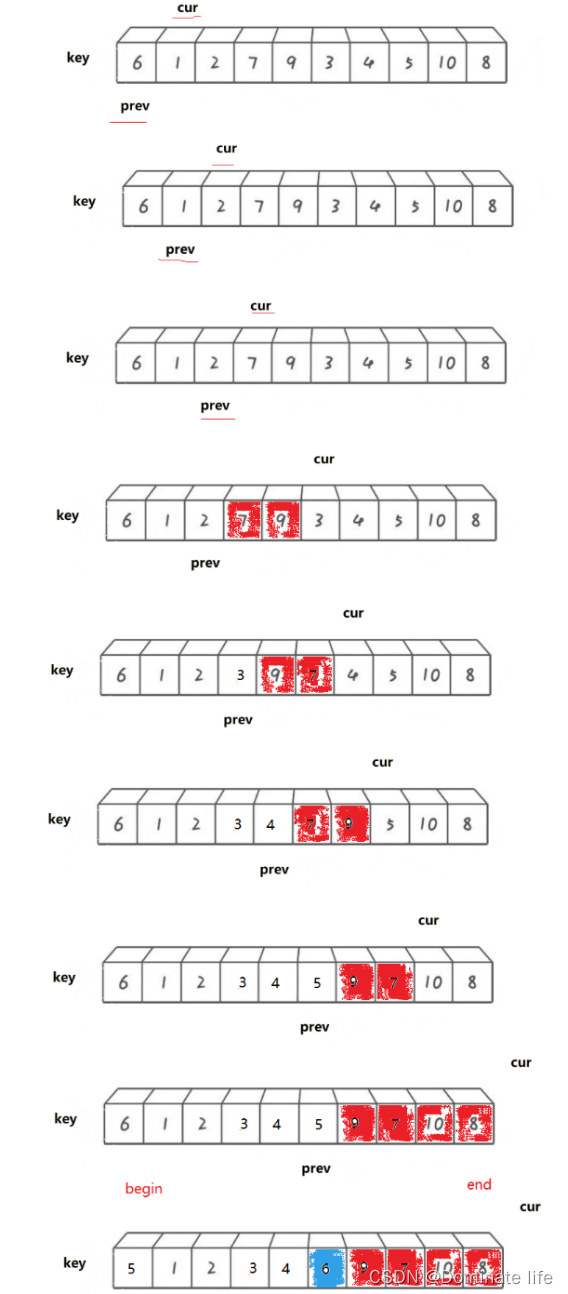
双指针代码实现

快排非递归实现

        快排递归我们不能直接转成非递归实现，需要用到数据结构：栈。因为我们要用循环和栈来模拟实现递归的效果。每次找到keyi的位置后要拆分成左和右两个区间，而拆出来的左区间就也是要找它的keyi位置再拆分的，不断的拆左区间，直到拆到的区间只剩一个元素或者没有元素才结束，然后由于栈的特性，左区间全部拆完后，才轮到右边，拆解右区间也是同理。总拆解过程就是把一个一个区间的范围存储起来，保持后进先出的规则，直到栈内没有然后元素就说明排序完成。

        例如下图，假设有十个数，拆解范围为0-9，对应的keyi位置下标为5，所以拆为0-4和6-9两个区间，因为0-4后入栈，所以有限拆0-4，直到把0-4范围拆解完毕才会去拆解6-9，就是一个模拟递归的过程。

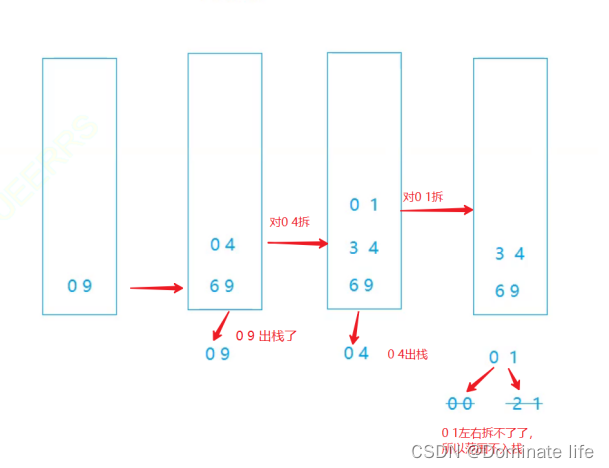
快排非递归代码：

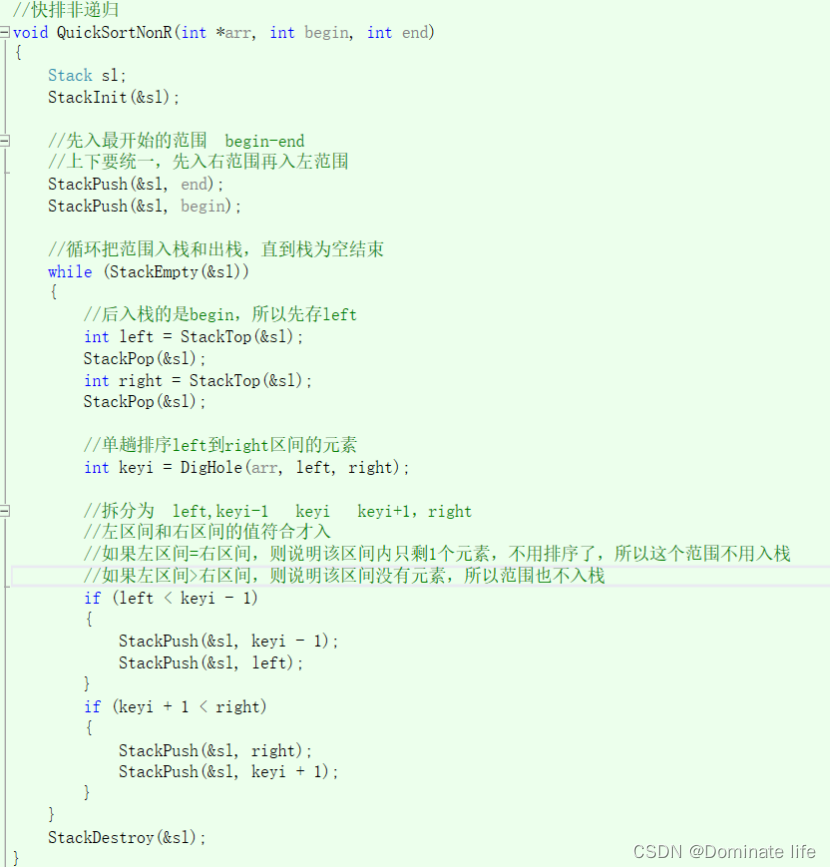
//快排非递归
void QuickSortNonR(int *arr, int begin, int end)
{
	Stack sl;
	StackInit(&sl);
 
	//先入最开始的范围  begin-end
	//上下要统一，先入右范围再入左范围
	StackPush(&sl, end);
	StackPush(&sl, begin);
 
	//循环把范围入栈和出栈，直到栈为空结束
	while (StackEmpty(&sl))
	{ 
		//后入栈的是begin，所以先存left
		int left = StackTop(&sl);
		StackPop(&sl);
		int right = StackTop(&sl);
		StackPop(&sl);
 
		//单趟排序left到right区间的元素
		int keyi = DigHole(arr, left, right);
 
		//拆分为  left,keyi-1   keyi   keyi+1，right
		//左区间和右区间的值符合才入
		//如果左区间=右区间，则说明该区间内只剩1个元素，不用排序了，所以这个范围不用入栈
		//如果左区间>右区间，则说明该区间没有元素，所以范围也不入栈
		if (left < keyi - 1)
		{
			StackPush(&sl, keyi - 1);
			StackPush(&sl, left);
		}
		if (keyi + 1 < right)
		{
			StackPush(&sl, right);
			StackPush(&sl, keyi + 1);
		}
	}
	StackDestroy(&sl);
}