java数据结构PriorityQueue_java priorityqueue的遍历

PriorityQueue

PriorityQueue 是具有优先级别的队列，优先级队列的元素按照它们的自然顺序排序，或者由队列构造时提供的 Comparator 进行排序，这取决于使用的是哪个构造函数

图像

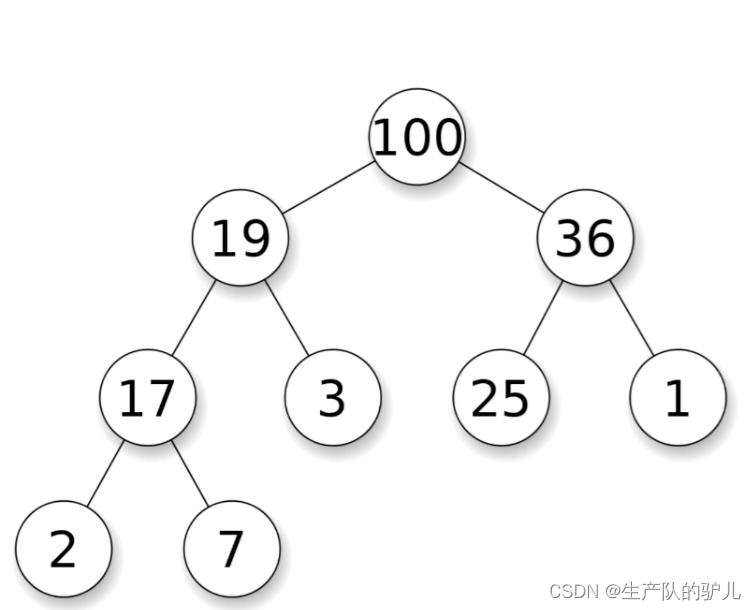
手写实现PriorityQueue

通过链表结构实现

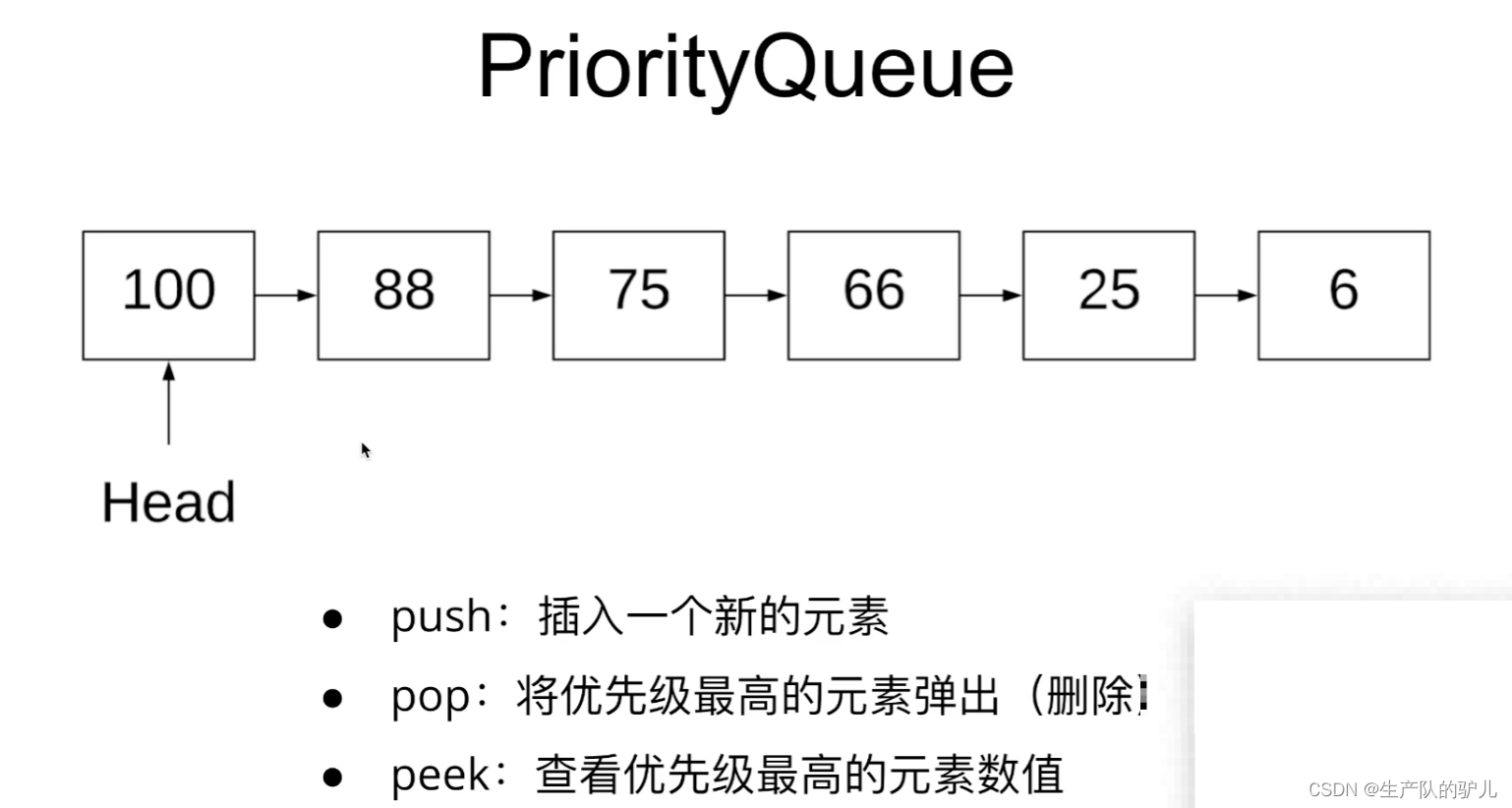
class PriorityQueue{
    static class Node{
        int val;
        int priority; // 优先级 Prioritization
        Node next;

        public Node(int value, int priority) {
            this.val = value;
            this.priority = priority;
        }
    }

    Node head = null;


    public void push(int val, int priority) {
        if (head == null) {
            head = new Node(val, priority);
            return;
        }
        Node cur = head;
        Node newNode = new Node(val, priority);

        // 当新节点的优先级 高于 head节点
        if (head.priority < priority) {
            newNode.next = head;
            this.head = newNode;
        } else {
            while (cur.next != null && cur.next.priority > priority) {
                cur = cur.next;
            }
            newNode.next = cur.next;
            cur.next = newNode;
        }
    }

    public Node peek(){
        return head;
    }

    public Node pop(){
        if(head == null) return null;
        Node temp = head;
        head = head.next;
        return temp;
    }
    public boolean isEmpty(){
        return head == null;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

时间复杂度分析
push O(n）
peek O(1)
pop O(1)
isEmpty O(1)

那么可以考虑优化push的时间复杂度

是用heap 进行优化

insert 插入节点

poll删除节点

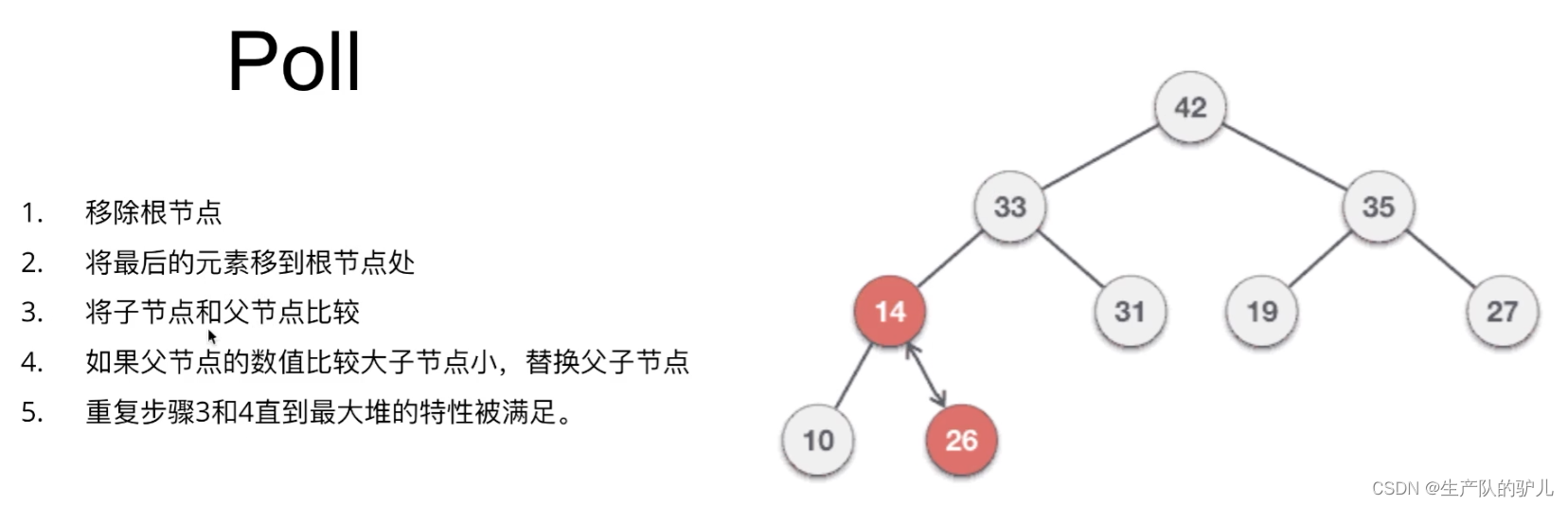
heap本质 是一个 平衡二叉树 balance binary search tree

import java.util.Arrays;
import java.util.NoSuchElementException;


// 使用array 作为 数据的容器 模拟 heap
// Simulate heap using array as the container of data
public class Maxheap{
    private int capacity; // 容量

    // 每添加一个新元素 size加一
    // 每减少一个旧元素 size减一
    // 当size 等于 capacity的时候，需要将 容量翻倍增加

    private int size = 0;
    private int[] array;

    // 构造器 constructor
    // 根据capacity to
    public Maxheap(int capacity) {
        this.capacity = capacity;
        this.array = new int[capacity];
    }

    private int getLeftChildIndex(int parIndex){
        return 2 * parIndex + 1;
    }

    private int getRightChildIndex(int parIndex){
        return 2 * parIndex + 2;
    }

    private int getParentIndex(int chIndex){
        return (chIndex - 1) * 2;
    }

    private boolean hasLeftChild(int index){
        return getLeftChildIndex(index) < size;
    }

    private boolean hasRightChild(int index) {
        return getRightChildIndex(index) < size;
    }

    private boolean hasParent(int index) {
        return getParentIndex(index) >= 0;
    }

    private int leftChild(int parIndex) {
        return array[getLeftChildIndex(parIndex)];
    }

    private int rightChild(int parIndex) {
        return array[getRightChildIndex(parIndex)];
    }

    private int parent (int chIndex) {
        return array[getParentIndex(chIndex)];
    }

    // time complexity: O(logN)
    private void insert(int item) {
        if (size == capacity) { // 扩大数组容量 Expand array capacity
            array = Arrays.copyOf(array, capacity * 2);
            capacity *= 2;
        }
        array[size] = item;
        size++;
        heapifyUp(); // 使用相同的方式 来处理这个节点  Use the same method to handle this node 
    }

    private void heapifyUp(){
        int index = size - 1;
        // 判断当前节点有无父节点 Determine whether the current node has a parent node
        // 如果新增节点 有 父节点 If the new node has a parent node
        // 且 父节点 < array[index]的元素
        // 那么 交换 父节点 和 该节点 位置 并更新
        while (hasParent(index) && parent(index) < array[index]) {
            swap(getParentIndex(index), index);
            index = getParentIndex(index);
        }
    }
    
    // remove the top element from heap
    private void poll(){
        if (size == 0) {
            throw new NoSuchElementException();
        }
        int element = array[0];
        array[0] = array[size - 1];
        // delete the first element
        // Replace the first element with the last element.
        size--;
        heapifyDown();
    }

    private void heapifyDown(){
        int index = 0;
        while (hasLeftChild(index)) {
            int largeChildIndex = getLeftChildIndex(index);
            if (hasRightChild(index) && rightChild(index) > leftChild(index)) {
                largeChildIndex = getRightChildIndex(index);
            }
            if (array[index] < array[largeChildIndex]) {
                swap(index, largeChildIndex);
            } else {
                break;
            }
            // 将large 赋值 给index 
            // Assign large to index
            index = largeChildIndex;

        }
    }

    public int peek(){
        if (size == 0) {
            throw new NoSuchElementException();
        }
        return array[0];
    }

    private void swap(int a, int b) {
        int temp = array[a];
        array[a] = array[b];
        array[b] = temp;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127

java中 constructor 构造函数

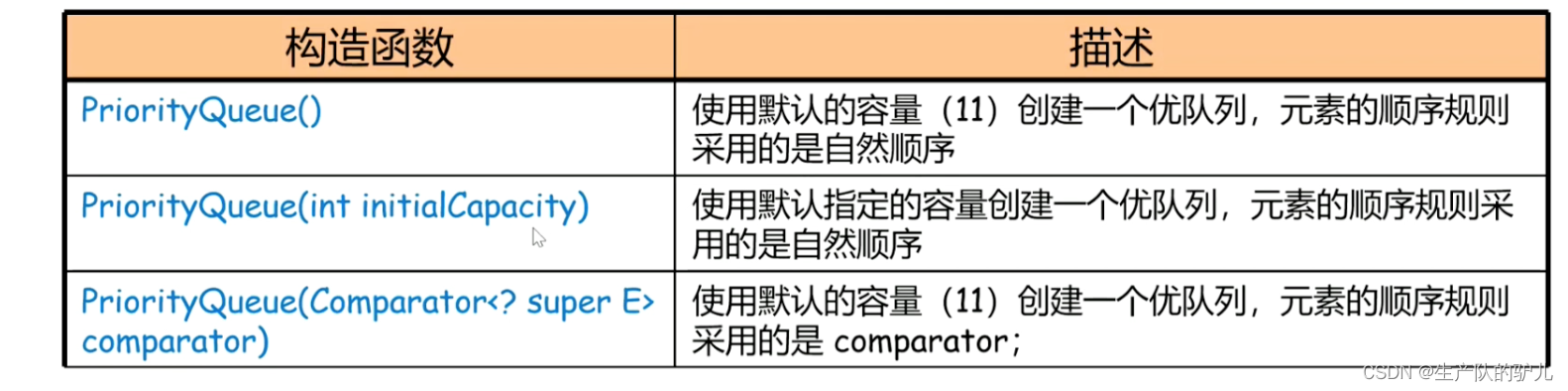
例子

import java.util.PriorityQueue;

class Customer implements Comparable<Customer>{
    String name;
    int level;

    public Customer(String name, int level) {
        this.name = name;
        this.level = level;
    }

    @Override
    public String toString() {
        return "Customer{" +
                "name='" + name + '\'' +
                ", level=" + level +
                '}';
    }

    @Override
    public int compareTo(Customer o) {
        return this.level - o.level;
    }
}

public class Solution {
    public static void main(String[] args) {
        PriorityQueue<Customer> pq = new PriorityQueue<>();

        pq.add(new Customer("张飞",1));
        pq.add(new Customer("关羽",2));
        pq.add(new Customer("诸葛亮",1));
        pq.add(new Customer("孙权",3));
        pq.add(new Customer("曹操",10));
        pq.add(new Customer("刘备",1));

        while (!pq.isEmpty()) {
            System.out.println(pq.poll());
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

结果

Customer{name='张飞', level=1}
Customer{name='刘备', level=1}
Customer{name='诸葛亮', level=1}
Customer{name='关羽', level=2}
Customer{name='孙权', level=3}
Customer{name='曹操', level=10}
1
2
3
4
5
6

练习leetcode

给定无序数组array，长度为n，将数组排成有序序列要求时间复杂度为O(NlogN)，空间复杂度为O(1）

Kth Largest Element in an Array leetcode 215

https://leetcode.com/problems/kth-largest-element-in-an-array/submissions/902686980/

遍历数组
创建pq
直接 往pq中插入数字
当数字容量大于k的时候，弹出顶端元素，因为顶上面的元素最大
遍历完数组之后，留下来的就是 前k个最小数了
返回 pq的顶上，就是 第 k个最小值

使用max heap
如果 元素容量超过 k了，我们就丢弃掉最大的那个
始终保持 pq中只有 k个元素
If the element capacity exceeds k, we will discard the largest one
Always keep only k elements in pq

class Solution {
    public int findKthLargest(int[] nums, int k) {
        PriorityQueue<Integer> pq = new PriorityQueue();
        for (int num: nums) {
            pq.offer(num);

            if (pq.size() > k) pq.poll();
        }
        return pq.peek();
    }
}
1
2
3
4
5
6
7
8
9
10
11

Top K Frequent Elements 347

Given an integer array nums and an integer k, return the k most frequent elements. You may return the answer in any order.

题目理解

给了n个数
这些数字 无序
而且 有重复

需要找出 k个最常出现的数

思路

首先 通过hashmap 对 数组中出现的数进行 统计频率
First, count the frequency of the number appearing in the array through hashmap

然后 创建priorityqueue， 规则 按照频率大小插入 pq中
最上面的元素 频率最小

遍历hashmap 将数字 插入 pq中
当 数组容器 小于 k时候，直接插入

大于k的话，比较 当前数的频率 和 数组中最小频率，如果大于后者
则插入 pq中
因为 我们只需要 最大的频率， 淘汰掉小频率，所以使用min heap在这里
选出最小的 然后 淘汰它
Because we only need the maximum frequency and eliminate the small frequency, we use min heap here
Select the smallest and eliminate it

class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        Map<Integer, Integer> map = new HashMap<>();
        for (int num: nums) {
            map.put(num, map.getOrDefault(num,0) + 1);
        }
		// 小顶堆，最上面的元素 频率最小
        PriorityQueue<int[]> pq = new PriorityQueue<>((pair1,pair2) -> pair1[1] - pair2[1]);

        for (Map.Entry<Integer,Integer> entry: map.entrySet()) {
            int[] pair = new int[2];
            pair[0] = entry.getKey();
            pair[1] = entry.getValue();

            if (pq.size() < k) {
                pq.add(pair);
            } else {
                if (pair[1] > pq.peek()[1]) {
                    pq.poll();
                    pq.add(pair);
                }
            }
        }

        int[] res = new int[k];

        for(int i = k - 1; i >= 0; i--) {
            res[i] = pq.poll()[0];
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

merge k sorted lists leetcode 23

合并 k个链表

思路

创建priorityqueue 然后，是 min heap
(a,b) -> a-b 这种

pq中存放ListNode类型，比较为node.val大小
创建 辅助空链表 dummyNode
首先将k 个头 存放到pq中

然后 while pq is not empty
就 将 pq取出的小节点 往后遍历一个
然后 将小节点 连接到 辅助 dummyNode上

代码

class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        if (lists == null || lists.length == 0) {
            return null;
        }

        PriorityQueue<ListNode> pq = new PriorityQueue<>((a,b) -> a.val - b.val);

        ListNode dummy = new ListNode(-1);
        ListNode cur = dummy;
        for(ListNode head: lists) {
            if (head != null) {
                pq.offer(head);
                head = head.next;
            }        
        }

        while (!pq.isEmpty()) {
            ListNode node = pq.poll();
            cur.next = node;
            cur = cur.next;
            if (node.next != null) {
                node = node.next;
                pq.offer(node);
            }
        }

        return dummy.next;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

单调递增序列 leetcode239

本题 使用的是 monotonic queue 和 priorityqueue 有一点点关系
但是 也可以说没关系

monotonic queue
单调队列： 队列中的元素全都是单调递增（或递减）的

题目理解

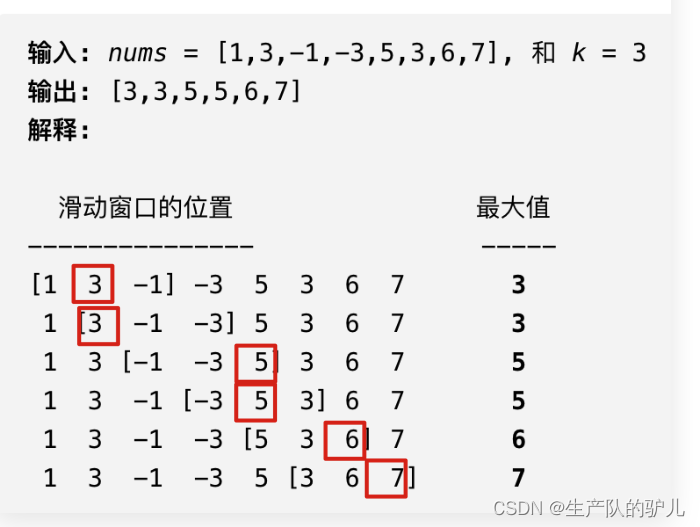
思路

每次找到 window中的最大值，然后添加到 res中，最后返回res数组。
首先考虑 priorityqueue， max heap，top值就是最大值，每次添加， 直接将top值加入res就好
但是 pq结构没有 考虑，到元素 添加 进去之后，如果溢出 最先进入的元素的话，怎么办
pq没有 考虑 元素的 添加顺序。

给你一个数组 window，已知其最值为 A，
如果给 window 中添加一个数 B，那么比较一下 A 和 B 就可以立即算出新的最值；

但如果要从 window 数组中减少一个数，就不能直接得到最值了，因为如果减少的这个数恰好是 A，就需要遍历 window 中的所有元素重新寻找新的最值。

class MonotonicQueue{
    LinkedList<Integer> q = new LinkedList<>();

    public void push(int x) {
        while (!q.isEmpty() && q.getLast() < x) {
            q.pollLast();
        }
        q.addLast(x);
    }

    public int max(){ return q.getFirst();}

    public void pop(int x){
        if (x == q.getFirst()) {
            q.pollFirst();
        }
    }
}

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        MonotonicQueue win = new MonotonicQueue();
        List<Integer> res = new ArrayList<>();

        for (int i = 0; i < nums.length; i++) {
            if (i < k - 1) {
                win.push(nums[i]);
            } else {
                win.push(nums[i]);
                res.add(win.max());
                win.pop(nums[i - k + 1]);
            }
        }

        int[] out = new int[res.size()];
        for (int i = 0; i < res.size(); i++) {
            out[i] = res.get(i);
        }
        return out;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

对于 PrioriyQueue理解Tips

小顶堆
小顶堆 pq 理解成一个筛子，较大的元素会沉淀下去，较小的元素会浮上来；当堆大小超过 k 的时候，我们就删掉堆顶的元素，因为这些元素比较小，而我们想要的是前 k 个最大元素嘛。

References

https://turingplanet.org/2020/03/07/%e4%bc%98%e5%85%88%e9%98%9f%e5%88%97-priorityqueue/

https://labuladong.github.io/algo/di-yi-zhan-da78c/shou-ba-sh-daeca/dan-diao-d-32cd5/