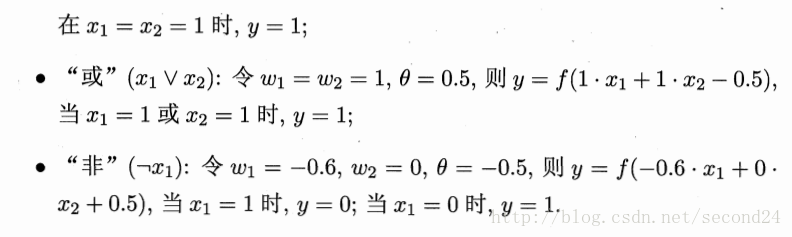机器学习--归纳总结_机器学习是归纳还是演绎

假设空间

归纳与演绎

归纳是从特殊到一般的“泛化”过程。演绎则是从一般到特殊的“特化”过程。“从样例中学习”显然是一个归纳的过程，因此也成为“归纳学习”。这又分为狭义和广义之分，广义的归纳学习大体相当于从样例中学习，而狭义的归纳学习则要求从训练数据中学得概念，因此也成为“概念学习”或“概念形成”。但是这种学习应用较少，因为要学得泛化性能好且语义明确的概念实在太困难了。

布尔概念学习

概念学习中最基本的是布尔概念学习，即对“是”“不是”这样的可表示为0和1布尔值的目标概念学习。以一个西瓜的数据集为例

版本空间

现实问题中我们常面临很大的假设空间，但学习过程是基于有限样本训练集进行的，因此，可能有多个假设与训练集一致，即存在着一个与训练集一致的“假设集合”，称为“版本空间”。西瓜问题对应的版本空间如图：

归纳偏好

归纳偏好可看作学习算法自身在一个可能很庞大的假设空间中对假设进行选择的启发式或“价值观”。

线性回归

基本形式

给定由d个属性描述的示例x=（x1;x2；…xd）,其中xi是x在第i个属性上的取值，线性模型试图学得一个通过属性的线性，线性模型试图学得一个通过属性的线性组合来进行预测的函数，即

f（x）=w1x1+w2x2+…+wdxd+b，
一般用向量形式写成

线性回归

对于离散属性，若属性值间存在“序”关系，可通过连续化将其转化为连续值，比如，二值属性“体重”的取值有“胖“ ”瘦”可转化为{1.0,0.0}，三值属性“高度”的取值“高”“中”“低”可转化为
{1.0,0.5,0.0};若属性值间不存在序关系，假定有k个属性值，则通常转化为k维向量，例如属性“瓜类”的取值“西瓜”“南瓜”“黄瓜”可转化为（0，0，1），（0，1，0），（1，0，0）。
线性回归试图学得一个一元函数，因此确定两个系数w和b尤为重要。均方误差是回归任务中最常用的性能度量，因此使试图让均方误差最小化，即

最小二乘“参数估计”

求解w和b使E 最小化的过程，称为线性回归模型的最小二乘“参数估计”。然后对这个的两个变量分别求导得到最优解

对数几率回归

这种回归主要用于分类任务，而在广义线性模型中，只需找一个单调可微函数将分类任务的真实标记y与线性回归模型的预测值联系起来。

单位阶跃函数

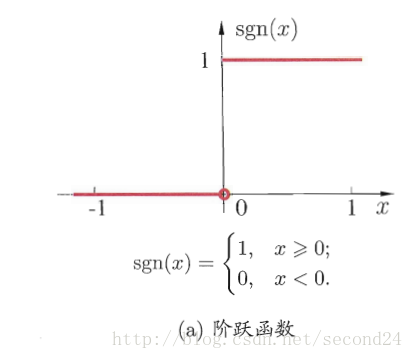
即z的值大于0就判为正例，小于零则判为反例，预测值为临界值零则可任意判别。

线性判别分析

线性判别分析的英文简称为ＬＤＡ，给定训练样例集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离；在对新样本进行分类时，将其投影到同样的这条直线上，再根据投影点的位置来确定新样本的类别。

如图：

多分类任务

多分类学习的基本思路是“拆解法”，即将多分类任务拆为若干个二分类任务求解。这里的关键是如何对多分类任务进行拆分，以及如何对多个分类器进行集成。

最经典的拆分策略有三种：

“一对一”（OVO）
“一对其余”（OvR）
“多对多”（MvM）

很明显看出，OvR只需训练N个分类器，而OvO需训练N（N-1）/2个分类器，因此，OvO的存储开销和测试时间开销通常比OvR大。但在训练时，OvR的每个分类器均使用全部训练样例，而OvO的每个分类器仅用到两个类的样例，因此，在类别很多时，OvO的训练时间开销通常比OvR小。
MvM是每次将若干类作为正类，若干个其他类作为反类。显然，OvO和OvR是MvM的特例。

神经网络

1. 神经元模型

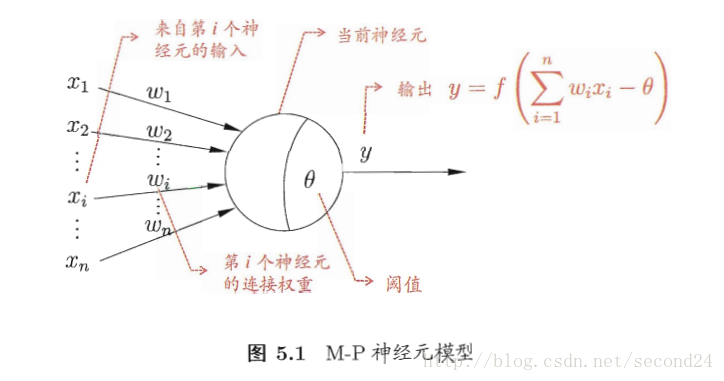
“M-P神经元模型”

在这个模型中，神经元接收到来自n个其他神经元传递过来的输入信号，这些输入信号通过带权重的连接进行传递，神经元接收到的总输入值与神经元的阈值进行比较，然后通过“激活函数”处理以产生神经元的输出。

原理图如下：

激活函数

主要分为两种形式
1. 阶跃函数

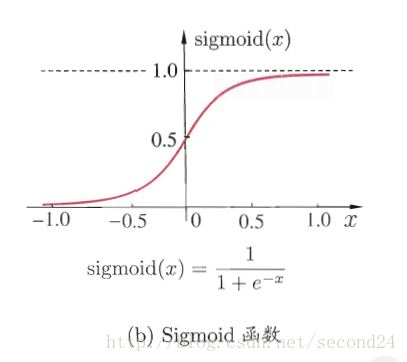
1. Sigmoid函数

2. 感知机与多层网络

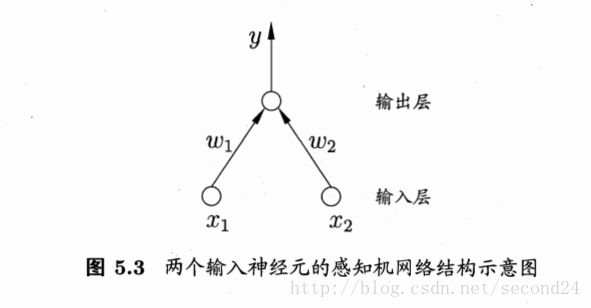
感知机由两层神经元组成，如图5.3所示，输入层接收外界输入信号后传递给输出层，输出层是M-P神经元（阈值逻辑单元）

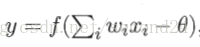
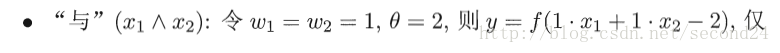
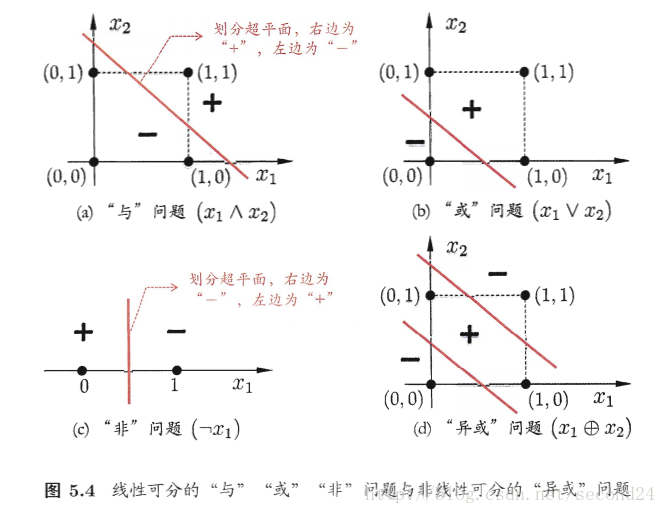
感知机能容易地实现逻辑与、或、非运算。注意到 ，假定f是图5.2中的阶跃函数，有

需要注意的是，感知机只有输出层神经元进行激活函数处理，即只拥有一层功能神经元，其学习能力非常有限。事实上，上述与、或、非问题都是线性可分的问题。

收敛：若两类模式是线性可分的，即存在一个线性超平面能将它们分开，则感知机的学习过程一定会收敛而求得适当的权向量；否则感知机学习过程将会发生震荡，权向量难以稳定下来，不能求得合适解。

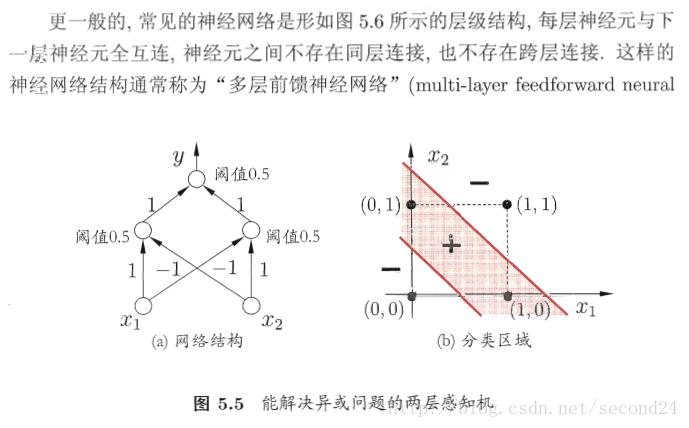
隐层

解决非线性可分问题，需考虑使用多层功能神经元。例如简单的两层感知机就能解决异或问题。输出层与输入层之间的一层神经元，被称为隐层或隐含层，隐含层和输出层神经元都是拥有激活函数的功能神经元。

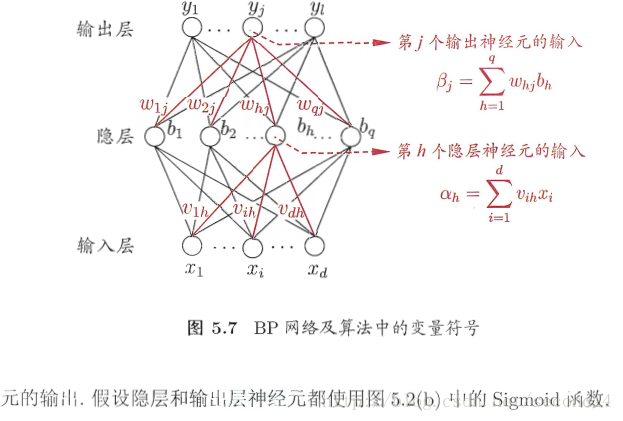
3. 误差逆传播算法

这种算法（简称BP）是为了训练多层网络，BP算法不仅可用于多层前馈神经网络，还可用于其他类型的神经网络，例如训练递归神经网络。

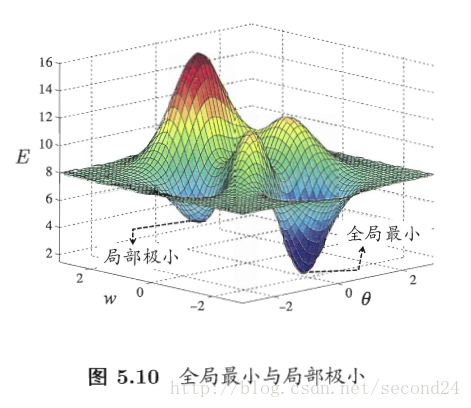
4. 全局最小和局部极小

若用E表示神经网络在训练集上的误差，则它显然是关于连接权w和阈值theta的函数。此时，神经网络的训练过程可看作一个参数寻优过程，即在参数空间中，寻找一组最优参数使得E最小。

我们在参数寻优过程中是希望找到全局最小。

参数寻优方法

基于梯度的搜索是使用最广泛的参数寻优方法。在此类方法中，我们从某些初始解出发，迭代寻找最优参数值。每次迭代中，我们先计算误差函数在当前点的梯度，然后根据梯度确定搜索方向。但是，若误差函数在当前点的梯度为零，则已达到局部极小，更新量将为0，这意味着参数的迭代更新将在此停止。显然，如果误差函数仅有一个局部极小，那么此时找到的局部极小就是全局最小；然而，如果误差函数具有多个局部极小，这显然不是我们希望的。

“跳出”局部极小

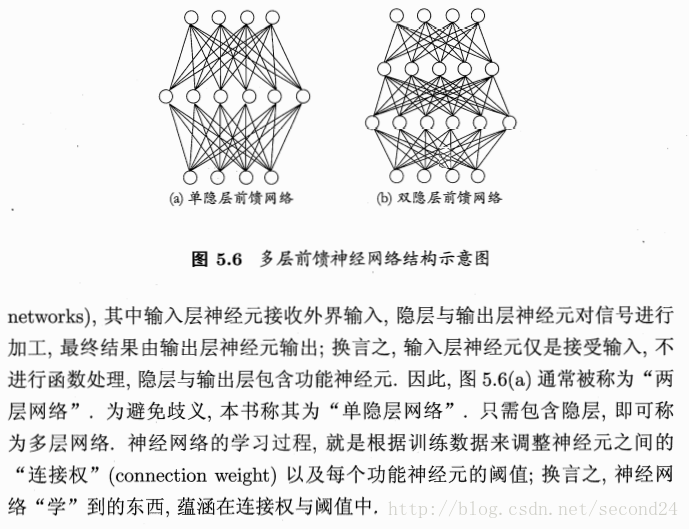
5. 其他常见神经网络

RBF网络

ART网络

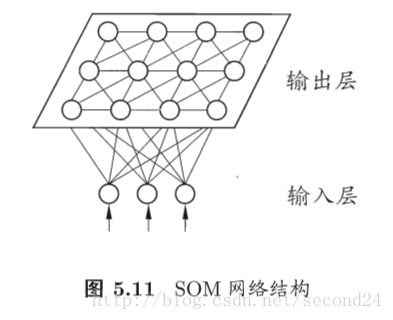
SOM网络

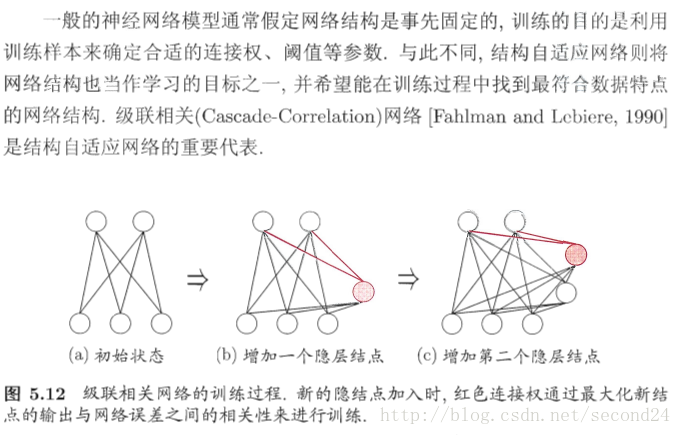
级联相关网格

支持向量机

1. 间隔与支持向量

为了对样本进行分类，需要在训练集中找到一个划分超平面，但能将样本分开的超平面有很多，按直观上看的话，应该去找位于两类训练样本“正中间”的划分超平面，如图。

在样本空间中，划分超平面可通过如下线性方程来描述：

至于间隔的话，我们可以通过约束参数w和b，使得r最大，来获得最大间隔。

由上式很容易看到，为了最大化间隔，只需最大化分母的-1次方，等价于最小化w的平方，于是，式6.5重写为

这就是支持向量机（SVM）的基本形。

2. 对偶问题

我们为了得到大间隔超平面所对应的模型，需要求出模型参数w和b。注意到式6.6是一个凸二次规划问题，能直接用现成的优化计算包求解，但我们可以有更高效的办法。

SMO算法

当求解式6.11 时， 不难发现，这是一个二次规划问题，如果使用通用的方法求解，那么会在实际中造成很大开销，因为该问题的规模正比于训练样本数。为了避开这个障碍，人们通过利用问题本身的特性，提出了很多高效算法，SMO是其中一个代表。

3. 核函数

当我们无法用一个划分超平面能将训练样本正确分类的时候，例如“异或”问题就不是线性可分的，对这样的问题，可将样本从原始空间映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分。例如在图6.3中，若将原始的二维空间映射到一个合适的三维空间，就能找到一个合适的划分超平面。而且只要满足原始空间是有限维，即属性数有限，那么一定存在一个高维特征空间使样本可分。

几种常用的核函数

4. 软间隔与正则化

有的时候，即便恰好找到了某个核函数使训练集在特征空间中线性可分，也很难断定这个貌似线性可分的结果不是由于过拟合造成的。

软（硬）间隔

缓解上述问题的一个方法是，允许支持向量机在一些样本上出错，为此，引入“软间隔”的概念，就是允许某些样本不满足约束条件，而前面几节的SVM的形式是要求所有样本均满足约束，即所有样本都必须划分正确，称为“硬间隔”。如图

当然，在最大化间隔的同时，不满足约束的样本应尽可能少。于是，优化目标可写为

显然，当C为无穷大时，式6.29迫使所有样本均满足约束（6.28），于是式（6.29）等价于（6.6）;当C取有限值时，式（6.29）允许一些样本不满足约束。

替代损失函数

5. 支持向量回归

6. 核方法

给定一些训练样本，若不考虑偏移项b，则无论SVM还是SVR，学得的模型总能表示成核函数的线性组合.

聚类

聚类任务

聚类是为了解决在无监督学习中，训练样本的标记信息是未知的。它试图将数据集中的样本划分为若干个通常是不相交的子集，每个子集称为一个“簇”。通过这样的划分，每个簇可能对应于一些潜在的概念，然而这些概念对聚类算法而言事先是未知的，聚类过程仅能自动形成簇结构，簇所对应的概念语义需由使用者来把握和命名。

例如在一些商业应用中需对新用户的类型进行判别，但定义“用户类型”对商家来说却可能不太容易，此时可先对用户数据进行聚类，根据聚类结果对每个簇定义为一个类，然后再基于这些类训练分类模型，用于判断新用户的类型。

聚类算法的基本问题

性能度量

聚类性能度量称为“有效性指标”。与监督学习中的性能度量作用类似，对聚类结果，我们需通过某种性能度量来评估好坏，另一方面，若明确了最终将要使用的性能度量，则可直接将其作为聚类过程的优化目标，从而更好地得到符合要求的聚类结果。
聚类性能度量大致有两类。一类是将聚类结果与某个“参考模型”进行比较，称为“外部指标”;另一类是直接考察聚类结果而不利用任何参考模型，称为“内部指标”。

距离计算

假如有个函数dist（,）,若它是一个“距离度量”，则需满足一些基本性质：

最常用的度量方法

连续属性和离散属性

我们常将属性划分为“连续属性”和“离散属性”，前者在定义域上有无穷多个可能的取值，后者在定义域上是有限个取值。而在讨论距离计算时，属性上是否定义了“序”关系更为重要。例如定义域{1,2,3}的离散属性与离散属性与连续属性的性质更接近一些，这样的属性称为“有序属性”；而定义域为{飞机，火车，轮船}这样的离散属性则不能直接在属性值上计算距离，称为“无序属性”。

VDM

原型聚类

原型聚类称为“基于原型的聚类”，此类算法假设聚类结构能通过一组原型刻画，在现实聚类任务中极为常用。通常情形下，算法先对原型进行初始化，然后对原型进行迭代更新求解。

k均值算法

具体的算法描述

学习向量量化

与k均值算法类似，“学习向量量化”也是试图找到一组原型来刻画聚类结构，但与一般聚类算法不同的是，ＬＶＱ假设数据样本带有类别标记，学习过程利用样本的这些监督信息来辅助聚类。

算法描述

高斯混合聚类

与前两个聚类结构不同，高斯混合聚类采用概率模型来表达聚类原型。

算法描述

密度聚类

密度聚类也称为“基于密度的聚类”，此类算法假设聚类结构能通过样本分布的紧密程度确定。通常情形下，密度聚类算法从样本密度的角度来考察样本之间的可连续性，并基于可连接样本不断扩展聚类簇以获得最终的聚类结果。

DBSCAN算法

它基于一组“邻域”参数来刻画样本分布的紧密程度。

算法描述

降维

k近邻学习

k近邻（简称kNN）学习是一种常用的监督学习方法，其工作机制是给定测试样本，基于某种距离度量找出训练集中与其最靠近的k个训练样本，然后基于这k个“邻居”的信息来进行预测。
图10.1给出了k近邻分类器的一个示意图。显然，k是一个重要参数，当k取不同值时，分类结果会有显著不同。另一方面，若采用不同的距离计算方式，则找出的“近邻”可能有显著差别，从而也会导致分类结果有显著不同。

低维嵌入

事实上，在高维情形下出现的数据样本稀疏，距离计算困难等问题，是所有机器学习方法共同面临的严重障碍，被称为“维数灾难”。
缓解维数灾难的一个重要途径是降维，亦成“维数约简”，即通过某种数学变换将原始高维属性空间转变为一个低维“子空间”，在这个子空间中样本密度大幅提高，距离计算也变得更为容易。

多维缩放（MDS）

这个算法用于，要求原始空间中样本之间的距离在低维空间中得以保持，即得到
“多维缩放”。

算法描述：

主成分分析

这也是一种最常用的降维方法。

算法描述：