Spark机器学习（二）-机器学习基础知识_spr chi 机器学习

目录

 

机器学习基础知识

机器学习流程

机器学习模型的分类

评估模型效果的指标

分类算法模型

回归算法模型

聚类算法模型

---

机器学习基础知识

这次主要是记录自己学习《Spark机器学习》这本书的学习过程，并不会长篇大论讲述机器学习的基础理论，这里简单点一下即可。

机器学习流程

机器学习流程主要可分为以下几部分：

1. 数据收集

2. 数据预处理

3. 特征工程

4. 模型训练

5. 模型测试验证

6. 模型部署上线

机器学习模型的分类

可以分为两大类：

监督学习：使用已标记数据来学习。“已标记”很关键，训练集必须是有标签的，不然就很难使用监督学习的模型。像经典的Kaggle的泰坦尼克号那个比赛就是典型的监督学习模型，还有一些推荐系统中用到的模型。监督学习一般都有2个主要任务：回归和分类。

回归：预测连续的、具体的数值。

分类：对各种食物分门别类，用于离散型预测。

常用的监督学习算法：

 

 

 

无监督学习：刚好和监督学习相反，训练过程中，不需要已标记的数据。模型会根据数据进行特征提取。一般都会用到聚类算法。如：

1. K均值聚类算法：是一种迭代求解的聚类分析算法，其步骤是，预将数据分为K组，则随机选取K个对象作为初始的聚类中心，然后计算每个对象与各个种子聚类中心之间的距离，把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。每分配一个样本，聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是没有（或最小数目）对象被重新分配给不同的聚类，没有（或最小数目）聚类中心再发生变化，误差平方和局部最小。

2. 分层聚类算法：对给定数据对象的集合进行层次分解，根据分层分解采用的分解策略，分层聚类法又可以分为凝聚的(agglomerative)和分裂的(divisive)分层聚类。

• 凝聚的分层聚类：它采用自底向上的策略，首先将每一个对象作为一个类，然后根据某种度量(如2个当前类中心点的距离)将这些类合并为较大的类，直到所有的对象都在一个类中，或者是满足某个终止条件时为止，绝大多数分层聚类算法属于这一类，它们只是在类间相似度的定义上有所不同。

• 分裂的分层聚类：它采用与凝聚的分层聚类相反的策略——自顶向下，它首先将所有的对象置于一个类中，然后根据某种度量逐渐细分为较小的类，直到每一个对象自成一个类，或者达到某个终止条件(如达到希望的类个数，或者2个最近的类之间的距离超过了某个阈值)。

1. 基于密度的聚类算法（DBSCAN，Density-Based Spatial Clustering of Applications with Noise）：与划分和层次聚类方法不同，它将簇定义为密度相连的点的最大集合，能够把具有足够高密度的区域划分为簇，并可在噪声的空间数据库中发现任意形状的聚类。

评估模型效果的指标

分类算法模型

准确率（Accuracy）

准确率计算公式：

Accuracy=(TP+TN) / (TP+FN+FP+TN)

即正确预测的正反样本数 / 总数

说明：

真正(True Positive , TP)：被模型预测为正的正样本。

假正(False Positive , FP)：被模型预测为正的负样本。

假负(False Negative , FN)：被模型预测为负的正样本。

真负(True Negative , TN)：被模型预测为负的负样本。

精确率（Precision）

精确率和准确率是不一样的，精确率只统计预测正确的正样本，并不是所有预测正确的样本。表示为预测出是正的里面有多少真正是正的，可理解为查准率。

公式：

Precision=TP / (TP+FP)

即正确预测的正样本数 / 预测正样本总数

召回率（Recall）

在实际正样本中，模型能预测出多少正样本。

公式：

Recall=TP / (TP+FN)

即正确预测的正样本数 / 实际正样本总数

F1 Score

F1 Score，是统计学中用来衡量二分类模型精确度的一种指标。它同时兼顾了分类模型的精确率和召回率。F1分数可以看作是模型精确率和召回率的一种调和平均，它的最大值是1，最小值是0。

公式：

F1 Score=2 * (Precision * Recall) / (Precision + Recall)

ROC曲线

指在特定刺激条件下，以被试在不同判断标准下所得的虚报概率P（y/N）为横坐标，以击中概率P（y/SN）为纵坐标，画得的各点的连线。

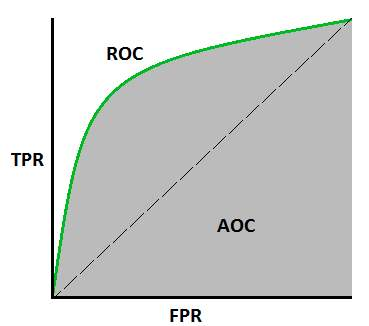
ROC曲线指受试者工作特征曲线 / 接收器操作特性曲线(receiver operating characteristic curve), 是反映敏感性和特异性连续变量的综合指标,是用构图法揭示敏感性和特异性的相互关系，它通过将连续变量设定出多个不同的临界值，从而计算出一系列敏感性和特异性，再以敏感性为纵坐标、（1-特异性）为横坐标绘制成曲线，曲线下面积越大，诊断准确性越高。在ROC曲线上，最靠近坐标图左上方的点为敏感性和特异性均较高的临界值。

总之：ROC曲线越接近左上角，该算法模型的性能越好。而且一般来说，如果ROC曲线是光滑的，那该算法模型就没有太大的过拟合。

AUC

AUC（Area Under Curve）被定义为ROC曲线下与坐标轴围成的面积，显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方，所以AUC的取值范围在0.5和1之间。AUC越接近1.0，检测方法真实性越高;等于0.5时，则真实性最低，无应用价值。

PR曲线

PR曲线实则是以precision（精准率）和recall（召回率）这两个为变量而做出的曲线，其中recall为横坐标，precision为纵坐标。

回归算法模型

平均绝对误差（MAE）

平均绝对误差是所有单个观测值与算术平均值的偏差的绝对值的平均。平均绝对误差可以避免误差相互抵消的问题，因而可以准确反映实际预测误差的大小

均方误差（MSE）

均方误差（mean-square error, MSE）是反映估计量与被估计量之间差异程度的一种度量。设t是根据子样确定的总体参数θ的一个估计量，(θ-t)2的数学期望，称为估计量t的均方误差。它等于σ2+b2，其中σ2与b分别是t的方差与偏倚。

均方根误差（RMSE）

均方根误差亦称标准误差，其定义为 ，i=1，2，3，…n。在有限测量次数中，均方根误差常用下式表示：√[∑di^2/n]=Re，式中：n为测量次数；di为一组测量值与真值的偏差。如果误差统计分布是正态分布，那么随机误差落在±σ以内的概率为68%。

决定系数

与复相关系数类似的，表示一个随机变量与多个随机变量关系的数字特征，用来反映回归模式说明因变量变化可靠程度的一个统计指标，一般用符号“R”表示，可定义为已被模式中全部自变量说明的自变量的变差对自变量总变差的比值。

聚类算法模型

兰德系数（Rand index）

用于聚类模型的性能评估，取值范围为[0,1]，值越大意味着聚类结果与真实情况越吻合。

互信息（Mutual Information）

互信息是信息论里一种有用的信息度量，它可以看成是一个随机变量中包含的关于另一个随机变量的信息量，或者说是一个随机变量由于已知另一个随机变量而减少的不肯定性。

轮廓系数

轮廓系数（Silhouette Coefficient），是聚类效果好坏的一种评价方式。它结合内聚度和分离度两种因素。可以用来在相同原始数据的基础上用来评价不同算法、或者算法不同运行方式对聚类结果所产生的影响。