【排序算法】插入排序和希尔排序

制作不易，三连支持一下吧！！！

---

---

前言

从这篇博客开始，我们将介绍几种常见的排序算法！

插入排序算法是希尔排序的基础，所以理解希尔排序前一定要先理解插入排序！！！

---

一、插入排序的原理及实现

相信大家在日常生活中都打过扑克牌，当我们要整理牌序时，是不是就是将新摸到的牌直接插入到它合适的位置，然后再摸一张牌，循环上述过程，最后我们手里的牌都变得有序了。

我们这里要介绍的插入排序原理和整理扑克牌的原理是相同的。

插入排序的思想就是：假设前n项已经有序，然后将第n+1项插入进去，使得前n+1项也变得有序，循环往复，直到最后一个数据也插入有序后，整个数据就有序了。 

动画演示如下：

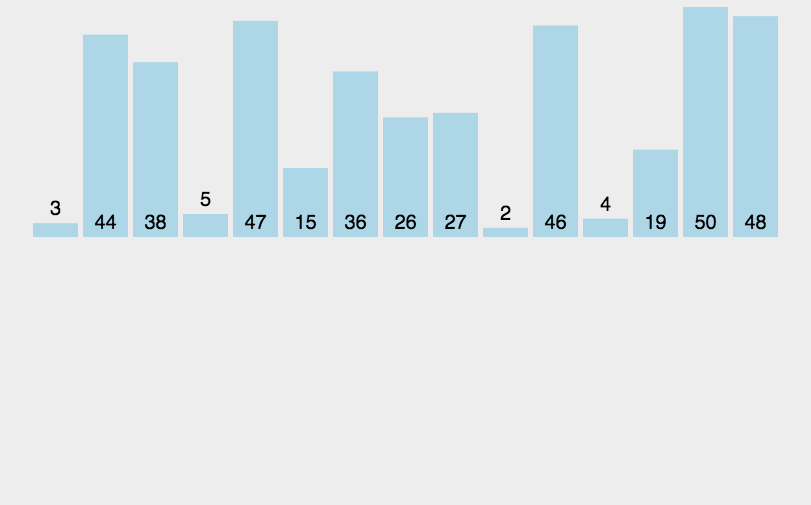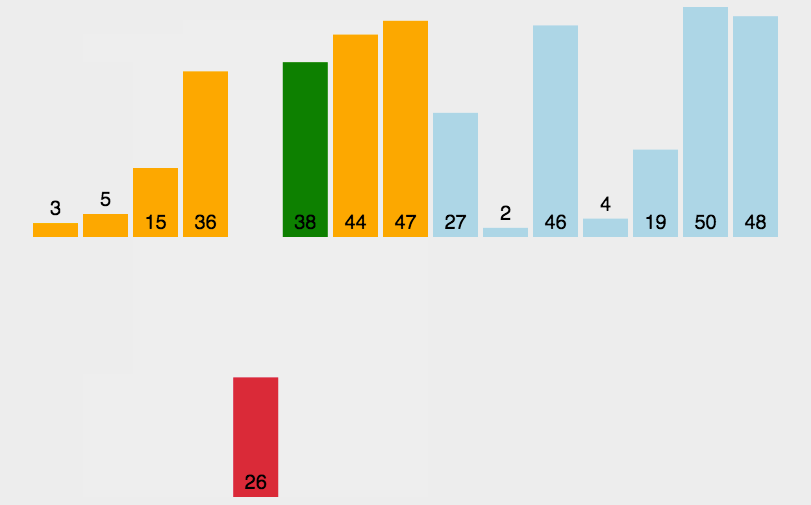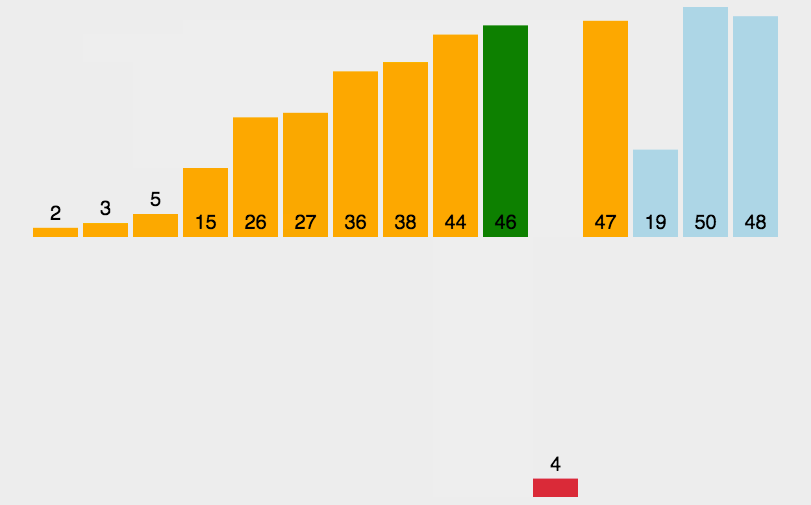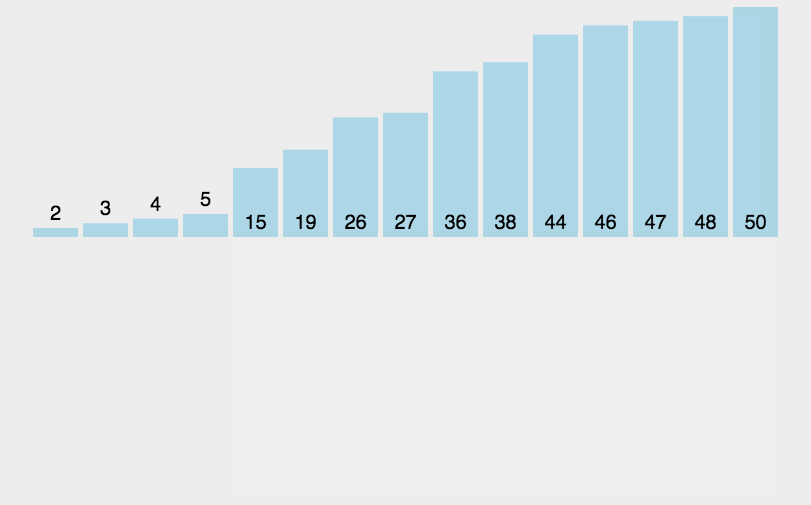
我们先来实现单趟插入排序

单趟插入排序就是在前面的有序序列中从后向前依次比较，假设我们要排成升序，那我们就要找比要插入的数据小的值，遇到比他大的值就继续向前，最后将新数据放到第一个比他小的值得后面。

代码实现：

		int end = i;
		int tmp = a[end + 1];
		while (end >= 0)
		{
			if (tmp < a[end])
			{
				a[end + 1] = a[end];
				end--;
			}
			else {
				break;
			}
		}
		a[end + 1] = tmp;

然后我们只需要让他循环单趟操作，并更新end的值即可。

注意因为我们这里新插入的元素的下标是end+1，所以end的范围应该是【0，n-2】，n是数组的元素个数。 

代码实现：

//直接插入排序
void InsertSort(int* a, int n)
{
	for (int i = 0; i < n - 1; i++)
	{
		int end = i;
		int tmp = a[end + 1];
		while (end >= 0)
		{
			if (tmp < a[end])
			{
				a[end + 1] = a[end];
				end--;
			}
			else {
				break;
			}
		}
		a[end + 1] = tmp;
	}
}

 

我们分析一下直接插入排序的时间复杂度：

按最坏的情况考虑，那就是所给序列与我们要排的序列是逆序的，这样我们每次插入新数据时都会插入在下标为0的位置，这种情况下每次插入的消耗是最大的。

这样可得O（N）=1+2+3+…+(n-1)=  .

所以时间复杂度为N^2.

二、希尔排序的原理及实现

希尔排序是希尔研究直接插入排序时发现，如果所给序列很接近有序，那么直接插入排序的效率就非常高，达到O（N），在排升序的情况下，他认为，如果新插入的元素较小，那么我们需要一步一步将他挪动到开头的位置处，这样操作效率太低。所以他就想到，以gap为间距，来进行直接插入排序，这样经过多次后，整个序列将会接近有序，最后再以gap为1进行一次直接插入排序，整个序列就有序了！！！

实现逻辑： 

① 先取一个小于n的整数d1作为第一个增量，把文件的全部记录分成d1个组。
② 所有距离为d1的倍数的记录放在同一个组中，在各组内进行直接插入排序。
③ 取第二个增量d2小于d1重复上述的分组和排序，直至所取的增量dt=1(dt小于dt-l小于…小于d2小于d1)，即所有记录放在同一组中进行直接插入排序为止。 

动图演示：

我们还是先来实现单趟：

 希尔排序的单趟与直接插入排序十分相似，因为希尔排序中的gap==1时就是直接插入排序。

int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
	if (tmp < a[end])
	{
		a[end + gap] = a[end];
		end -= gap;
	}
	else {
		break;
	}
}
a[end + gap] = tmp;

然后我们还是再套一层循环，让它重复上述过程。

for (int i = 0; i < n - gap; i++)
{
	int end = i;
	int tmp = a[end + gap];
	while (end >= 0)
	{
		if (tmp < a[end])
		{
			a[end + gap] = a[end];
			end -= gap;
		}
		else {
			break;
		}
	}
	a[end + gap] = tmp;
}

最后再套一层循环来实现不同gap的多次预排序。 

void ShellSort(int* a, int n)
{
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;
		for (int i = 0; i < n - gap; i++)
		{
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (tmp < a[end])
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else {
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}
}

最后，我们的希尔排序就写好了！！！ 

下面我们对希尔排序的性能分析一下：

希尔排序的时间复杂度难以计算，我们只能通过大量数据分析得出规律。

希尔排序的时间复杂度是 O (n^ (1.3-2)) ，空间复杂度为常数阶 O (1)1234。希尔排序的效率取决于它的增量序列5。希尔排序的基本思想是先将整个待排序列分割成若干个子序列，分别进行直接插入排序，然后依次缩减增量再进行排序，待整个序列中的记录“基本有序”时，再对全体记录进行一次直接插入排序2。希尔排序的时间复杂度与增量序列的选择有关，最坏情况下为O (n^2)，最好情况下为O (n log n)2

---

总结

希尔排序是直接插入排序的升级，我们理解了直接插入排序，希尔排序应该会很轻松。