动态规划——力扣篇_动态规划力扣

最长回文子串

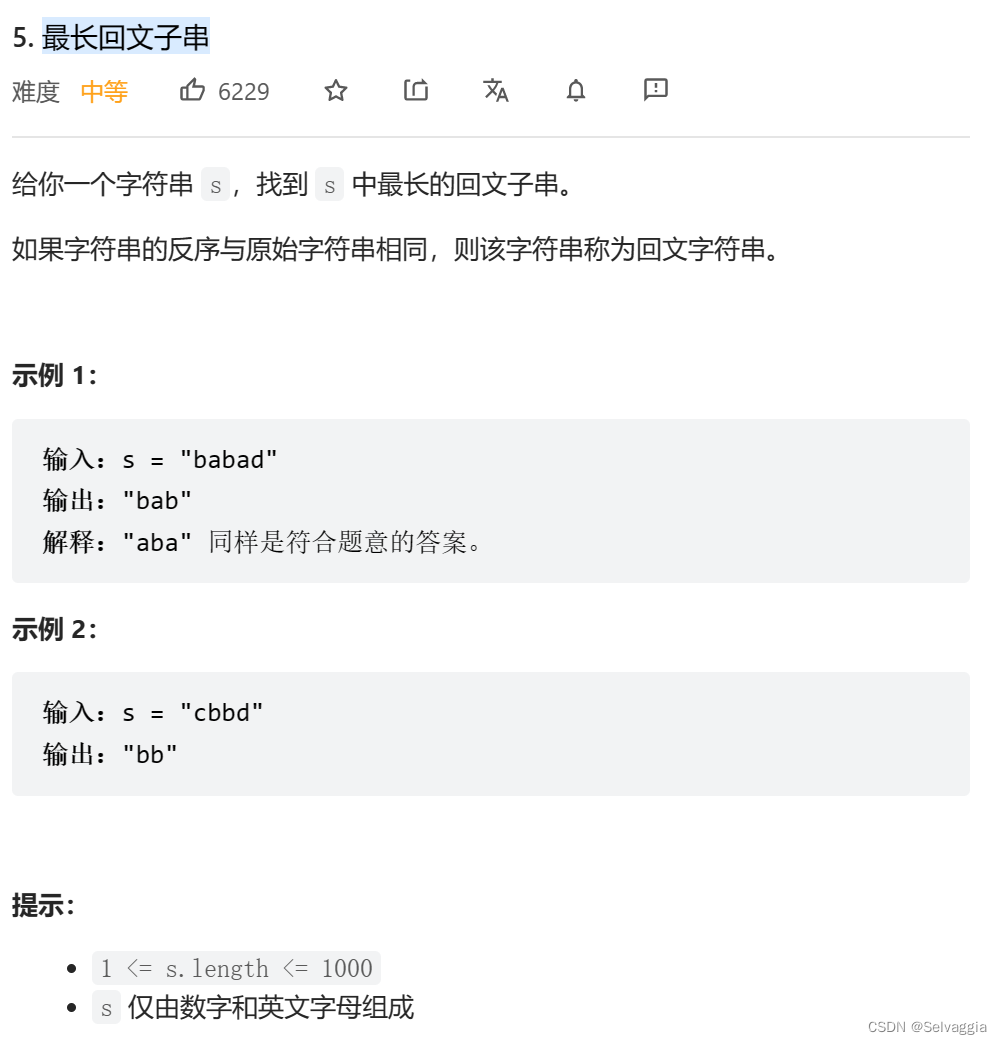
class Solution {
public:
    string longestPalindrome(string s) {//最长的回文子串
    	int n=s.size();
		vector<vector<bool> > dp(n,vector<bool>(n));
		for(int i=0;i<n;i++)dp[i][i]=true;
//		int maxlen=0;
//		int pos=-1; 太草率，要考虑没有一个长度大于1 的回文串，那输出就是 s[0]
		int maxlen=1;
		int pos=0;
		for(int len=2;len<=n;len++){//字符串枚举子串，最外层字串长度
			for(int i=0;i+len<=n;i++){
				int j=i+len-1;
//				dp[i][j]= dp[i+1][j-1] && (s[i]==s[j]);没考虑到j=i+1
				if(s[i]!=s[j]){
					dp[i][j]=false;
				}
				else{
					if(len==2)dp[i][j]=true;
					else dp[i][j]= dp[i+1][j-1];
				}
				if(dp[i][j]&&len>maxlen){
					maxlen=len;
					pos=i;
				}
			}
		}
		return s.substr(pos,maxlen);
    }
};
//暴力思想就是双重循环暴力枚举每个子串再判断是否是回文串
//dp[i][j]判断 [i,j]这段子串是否为回文串
//转移方程 s[i]==s[j] 则 dp[i][j]= dp[i+1][j-1] && s[i]==s[j]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

单词拆分

这里是线性dp，目前觉得，线性dp还是枚举左右端点的好（no，不是简单的双重循环枚举左右端点，动态规划基础题求最长上升子序列，啊，乱了，总之线性dp本来就是主打计算一重循环，另一重是为了判断，，，，看代码，对于$0$ ~ $i$这段，端点i能否可行，需要遍历$0$ ~ $i-1$是否有可行的并能转化到i状态，从而决定 $i$ 状态是否可以达成true
序列dp再考虑枚举子串长度和左端点
枚举方式 和 截取子串的长度涉及到下标，有点烦人
举个小规模例子来确定 i-j 要不要加1

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
    	set<string> S;
    	S.clear();
    	for(int i=0;i<wordDict.size();i++){
    		S.insert(wordDict[i]);
		}
    	int n=s.size();
		vector<bool> dp(n+1,false);
		dp[0]=true;
		//n+1因为这里需要初始化 最开始的下标前一个为true进行递推,因此dp下标从1开始计算
//		for(int len=1;len<=n;i++){
//			for(int i=0;i<n;i++){
//				int l=i+1;
//				int r=l+len-1;
//				dp[r]=dp[]
//			}
//		}
//		for(int i=1;i<=n;i++){
//			for(int j=i;j<=n;j++){
//				if(!dp[i])dp[j]=false;//不一定啊，可能i-1~j这个单词存在于字典
//				else{
//					string str=s.substr()
//				}
//			}
//		}
		for(int i=1;i<=n;i++){//s[i-1]  i 5(s[4])  j 2(s[2])   
			for(int j=0;j<i;j++){//s[j]
				if(dp[j]){
					string str=s.substr(j,i-j);
					if(S.find(str)!=S.end()){
						dp[i]=true;
						break;
					}
				}
				
			}
		}
		return dp[n];
    }
};
//暴力思想有点难达成
//动态规划 可以假设已经求解除了一部分
//dp[i]表示s[0,i]是否可以通过字典中单词表示，
//dp[j](i<j)=dp[i]&& s[i,j]这个单词是否存在于字典中
//大概思想是如上所写，但是由于下标的缘故dp[i]表示s[0,i-1]，
//即dp[i]的i表示的是s前i个字符是否可以用字典表示
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

未知由已知推到

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        vector<string>& w = wordDict;
        int n = s.size(), m = w.size();
        vector<bool> rec(n, false);
        rec[0] = true;
        for (int i = 0; i != n; i++) {
            if (rec[i]) {
                for (int j = 0; j != m; j++) {
                    int temp = s.find(w[j], i);
                    if (temp == i) {
                        if (i + w[j].size() == n)  return true;
                        else if (i + w[j].size() < n)
                            rec[i + w[j].size()] = true;
                    }
                }
            }
        }
        return false;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

单词拆分Ⅱ(递归+回溯（典型⭐））

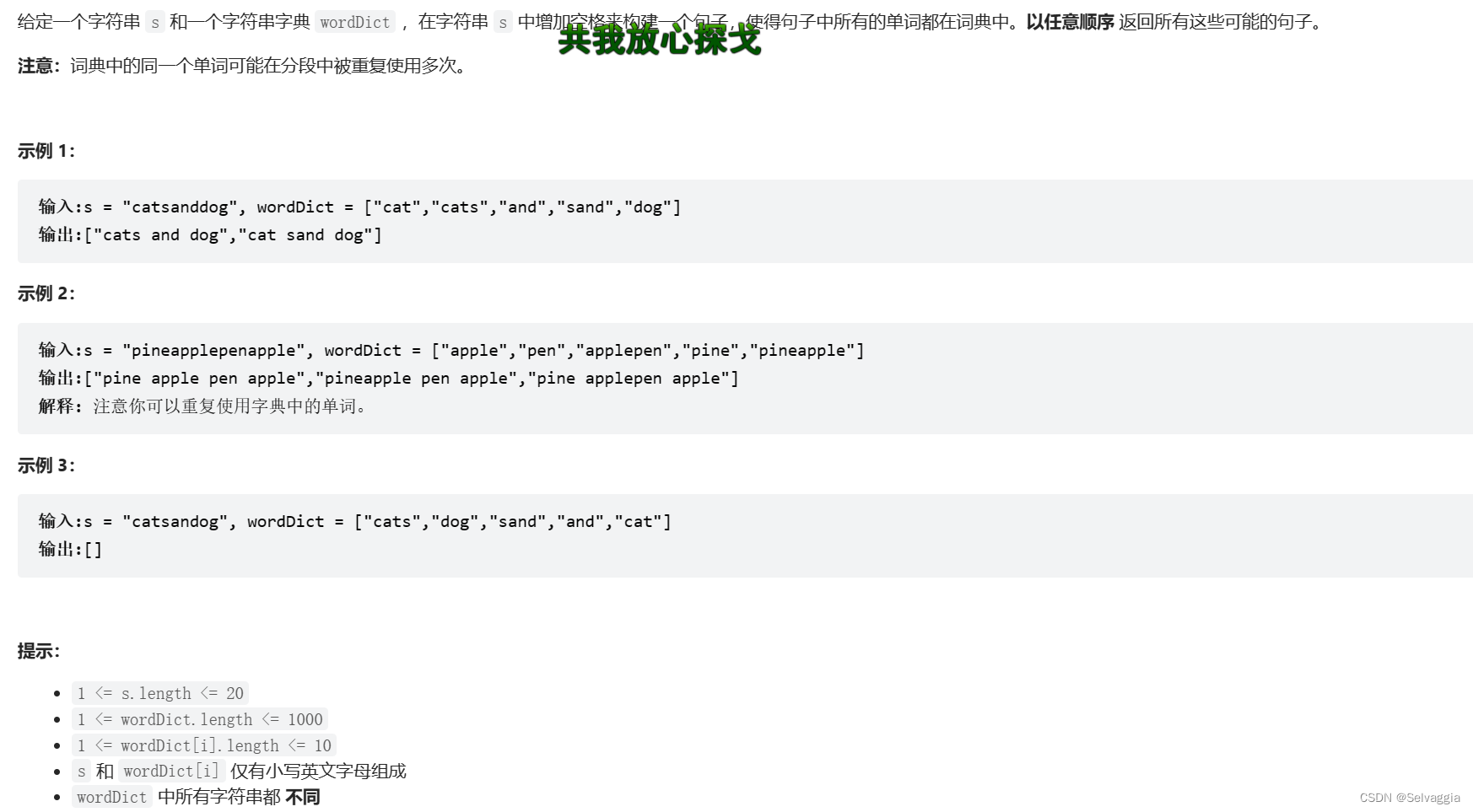
class Solution {
private:
	set<string> S;
	map<int,vector<string> > mp;//mp[i] s[i~n-1]的所有 拆分结果
public:
	void dfs(const string & s,int index){
		if (mp.count(index))return ;//剪枝，mp[index]对应的是
//		下标index之后字符串的所有拆分方式，是唯一的，如果已经计算出该结果，通过mp
//		避免重复计算，就像 sandfffff,fffff分割方式是固定的，只要用前面分割的单词
//		添加到mp[4]vector数字每一个字符串之前就好
		
//		错误想法
//一种分割方法就好，可能index会是不同种
//		catsand本来担心的是，假如字典中只有sand没有and，
//		那么如果选取了cats就无法成功分割
//		但是如果字典只有cats和sand，那么必定是无法分割的，一定还有cat
//		所以，我觉得先遇到的可以分割出去的单词一定要先分出去，
//		如果有答案这种做法一定能取得答案
		if(index==s.size()){
			mp[index].push_back("");
			return;
		}
//		mp[index] = {};//因为对于不同组的结果
//下标index之后字符串的拆分方式不同，但是已经剪枝，可以不需要
		for(int i=index+1;i<=s.size();i++){//为什么可以获得多组结果，catsand
//		先是cat，dfs("sand"),i继续后移，找到cats dfs("and")
			string str=s.substr(index,i-index);
			if(S.find(str)!=S.end()){
				dfs(s,i);//递归的妙处，
//等下标i之后的字符串根据字典划分出来之后便，再把划分结果添加到之前的尾部
				
//				if(mp[i].size()==0)mp[index].push_back(str);
//				else{
//					mp[index].push_back(str+" ");
//				}
//				for(auto tmp:mp[i]){//const string& tmp:
//					mp[index].push_back(tmp);
//				}此注释部分错误，输出所有分割可能而不是任意一个
				for (const string& succ: mp[i]) {
                       mp[index].push_back(succ.empty() ? str : str + " " + succ);
                }
			}
		}
	}
    vector<string> wordBreak(string s, vector<string>& wordDict){
    	
    	for(int i=0;i<wordDict.size();i++){
    		S.insert(wordDict[i]);
		}
    	
		dfs(s,0);
		return mp[0];
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55