[图形学渲染]大白话推导三维重建(二)-对极几何(Epipolar Geometry)、基础矩阵(Fundamental Matrix)、八点算法(Eight Point Algorithm)_基础矩阵一般推导

---

前言

本章将尽量以通俗易懂的方式推导三维重建中常用到的对极几何和基础矩阵的几个概念，涉及数学公式较多但并不困难，如有错误，欢迎指出。

书接上回： [图形学渲染]大白话推导三维重建(一)-摄像机内参外参、世界坐标转换、3D物体投影、单双目摄像头、视差

上文我们已经明白了3D空间中的一个点 Xw = [X, Y, Z] 是如何变换到 2D图像的一个像素点 x = [x, y] ：

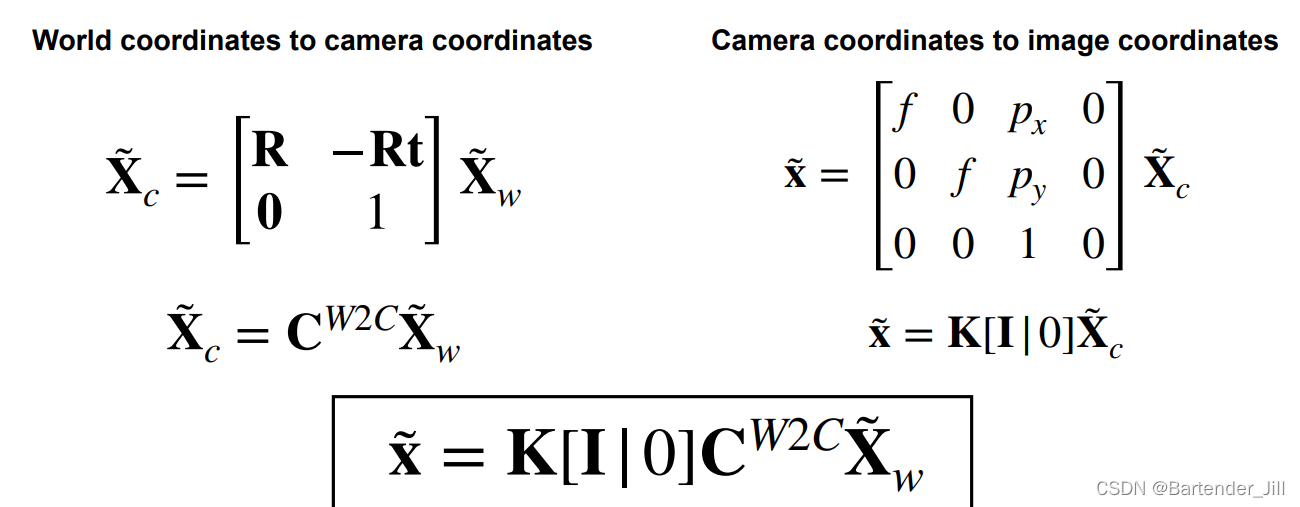
即：将世界坐标系下的一个3D点 $\widetilde{X_w}$ =(X,Y,Z) 转换成2D图像实际像素上的坐标点 $\tilde{x}$ = (x,y) 。

而三维重建则是将上述步骤反过来，要从2D图像恢复出3D场景，故我们最容易想到的便是对上面3D到2D的式子求逆运算。

但实际上2D图像恢复成3D场景还缺乏一个 深度信息 ，无法简单地通过公式求逆进行恢复，所以我们还要用双目摄像头计算出深度信息Z：

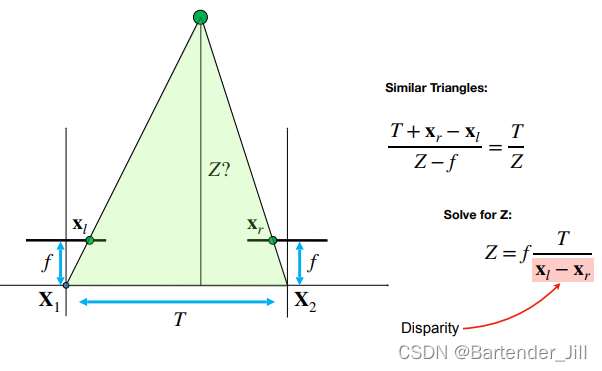
既然有了2D像素坐标(x,y)，以及双目摄像头计算得到的深度信息Z，那么从2D的(x, y)恢复成3D的(X,Y,Z)应该没什么问题吧？

但其实该推理过程都是在较为理想的情况下推导出来的，在现实中还会遇到许多问题：

1. 如何确保两个相机中的2D图像所看的 像素点 对应的是同一个3D空间中的点？
2. 如果两台摄像机的观看高度和角度发生变化怎么办？缺乏相对位姿信息便难以计算Z值，难道每次都要用设备测量一次两个摄像机的相对位姿信息?

为此，我们要引入对极几何( Epipolar Geometry ) 这个概念。

一、Epipolar Geometry （发音类似于Epic Polar）

1.1 背景知识

假设我们在用两个相机看同一个场景中的同一处物体，在图像上的成像位置分别是 x₁，x₂：

两个相机都有自己的相机平面，假设现在只看 相机1，该相机图像上有一点 x₁ ， 那么其可能对应空间上的哪些点呢：

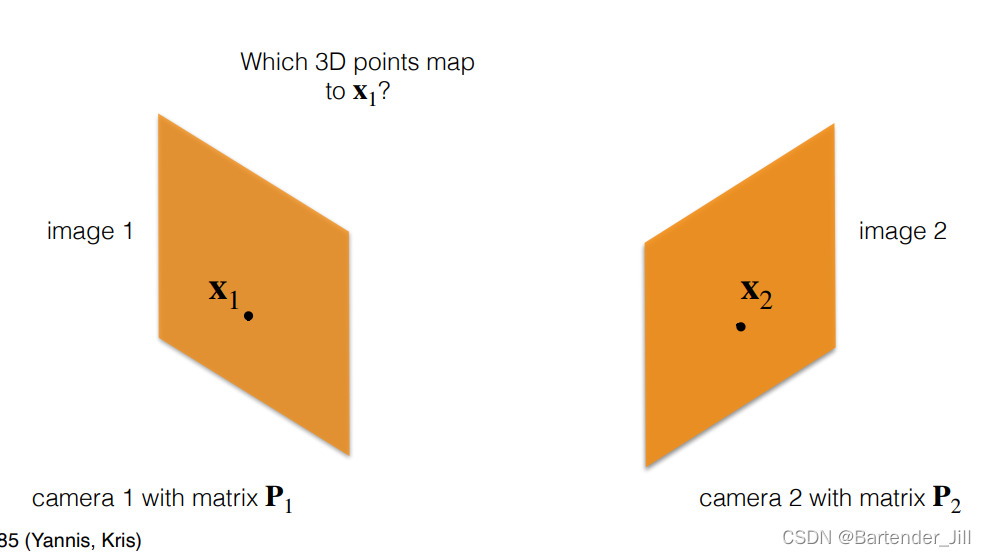
在缺乏深度信息的情况下，我们只能知道这个点对应一条直线：

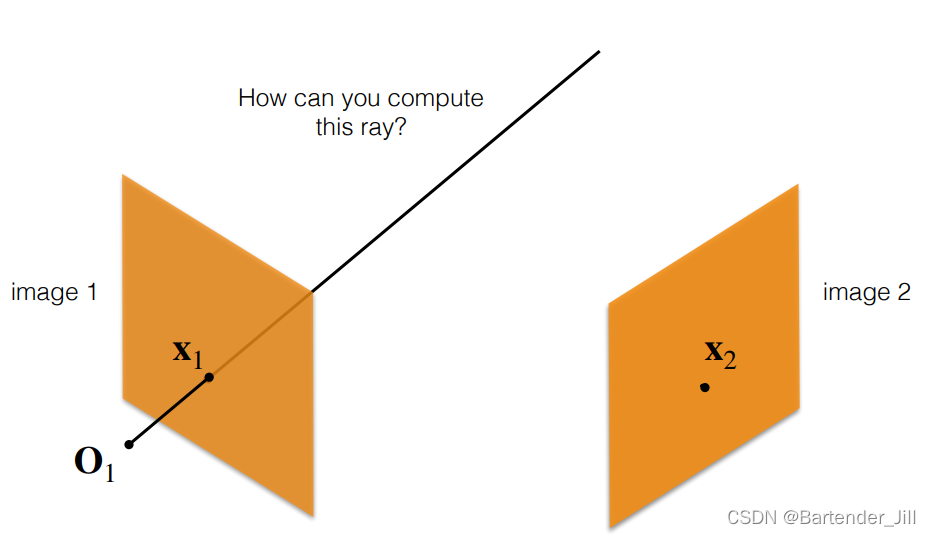
且该直线的方程可以表示为一个向量公式，即 摄像机原点的位置O1 + 2D点转3D点后的直线向量：

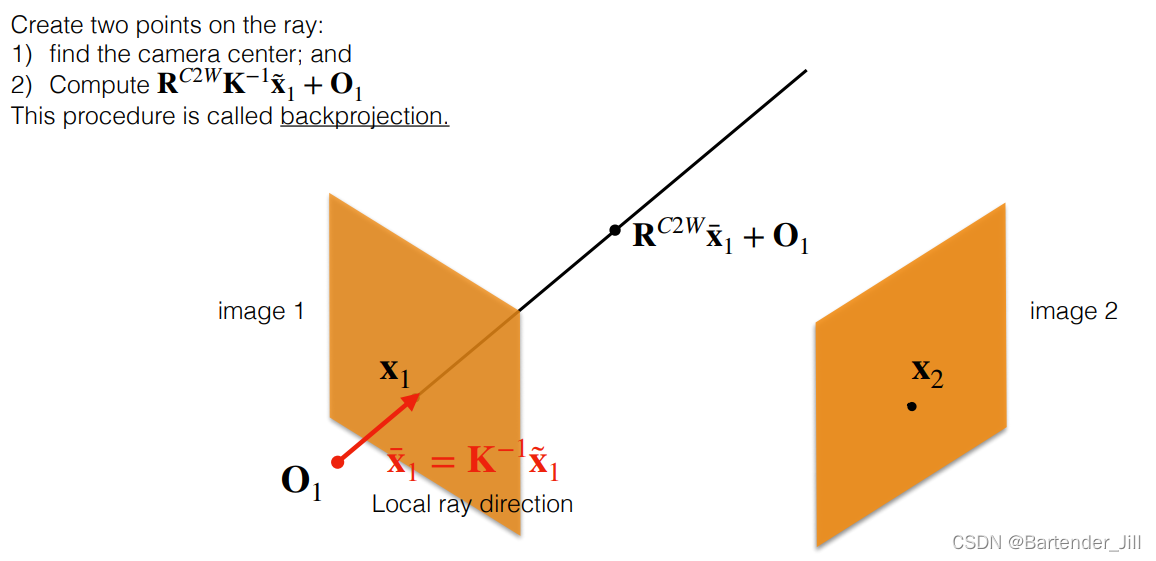
注：此时的 x₁ 是相机捕获到的图像上的一个 2D点，但并不是相机传感分辨率上的 x₁~ ，需要将其坐标进行换算才得到。

不太理解该公式推导的，可以详细下大白话推导三维重建(一)的第三章部分。

为什么要对该直线以参数的形式表达出来呢？ 因为参数化直线才方便后续求交点，求平面等运算。

现在问题来了，我们让相机2也对着 x2 发射一条射线，那这两条线可能会相交吗？

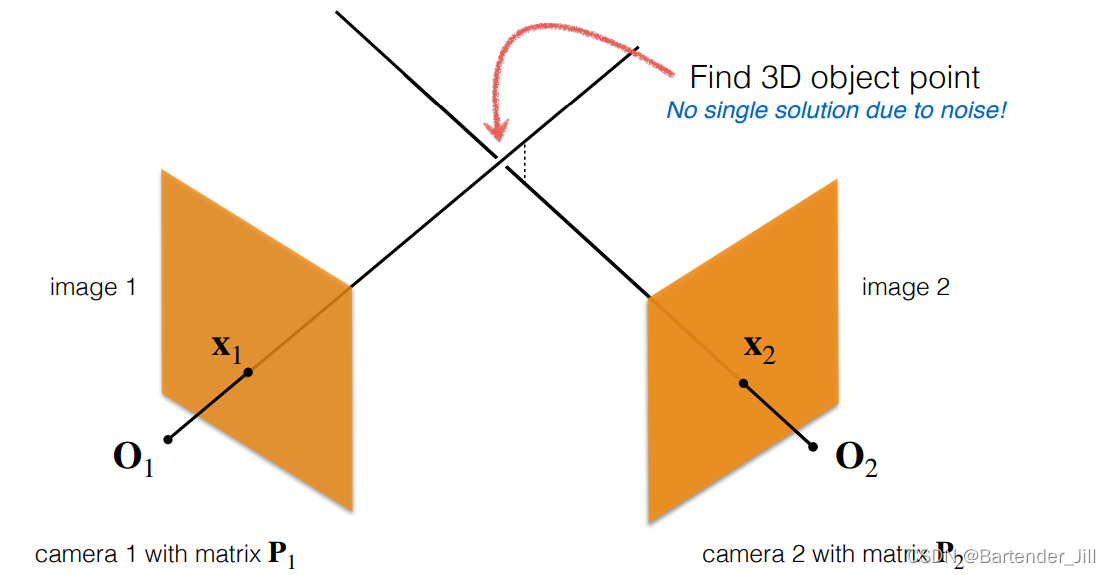
答案是不一定，相机拍摄的画面总带有一定噪声，你无法确保两个相机的拍摄到的两个像素点一定是对应同一个空间中的3D点，可能会有少许偏差。

除此之外，在现实生活中，有时我们并不知道相机的位姿状态。
比如举着个手机围绕客厅拍了一圈，相机的位姿是时时刻刻在变化的，我们难以知道其与世界坐标的转换关系：

没有位姿，就意味着难以计算出同一个场景在不同图像里的对应关系，不好计算出深度。

你可能会想：大部分情况下摄像机都是固定且数目很少，那直接利用物理测量手段(卷尺、激光等设备)测量摄像机的位姿信息不就行吗？

事实上，哪怕是相机很少且固定的情况，用 物理手段测量两相机之间相对位姿信息 也极其不方便，这就是为什么我们要学 对极几何 与 基础矩阵 等相关概念，它们能够帮我们恢复摄像机的位姿信息。

1.2 对极几何定义 （Epipolar Plane/Line/Pole）

假设已知两个相机的位姿信息P1和P2，且由于两张图像拍摄到的像素点不一定对应同一个3D空间中的点：

那么我们如何在 相机2 中找到 相机1 中的 x₁ 点？

或者说，这个 x₁ 点 最可能对应 相机2 图像中的哪个点？

我们不妨构造这样一个平面：

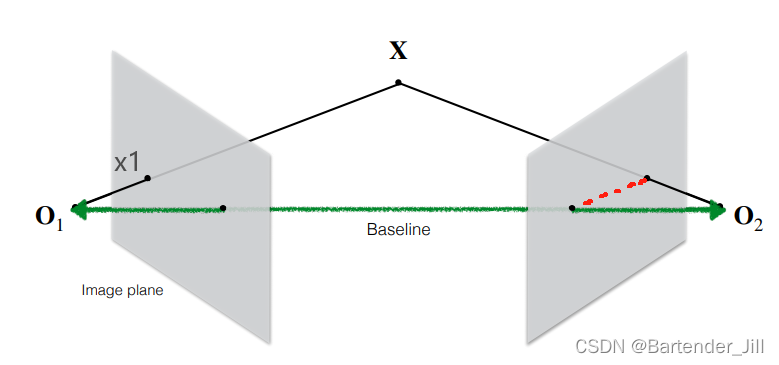
其中，Baseline 指的是两个相机位置之间的连线，红色虚线代表 相机2 所有可能的 x₁ 候选点所构成的直线。

这并不难理解，x₁ 在不知道具体深度的情况下，于3D空间中其实对应一条直线，x₁ 可以是该直线上任意的一个点。而这也意味着 x₁ 在相机2图像上的候选点也构成了一条直线。

不妨再严谨化一点，给这些东西取个学名：

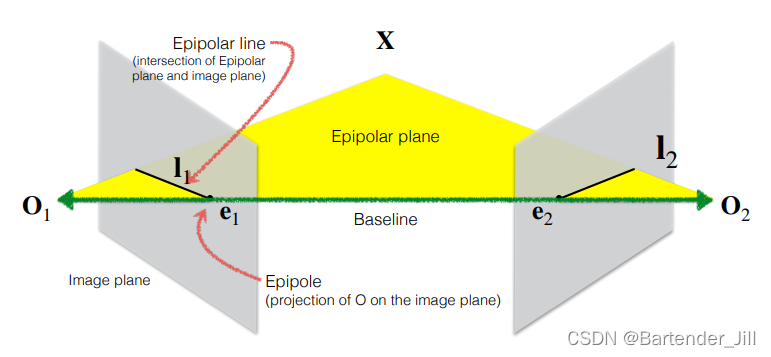
• O1-X-O2 构成的平面称为 Epipolar Plane。
• 候选点所构成的直线，即 相机平面 与 Epipolar Plane 的相交直线称之为 Epipolar line。
• O1-O2 连线在相机平面上的投影为 Epipole。

故 x₁ 在 相机2 上的候选点即为 I₂：

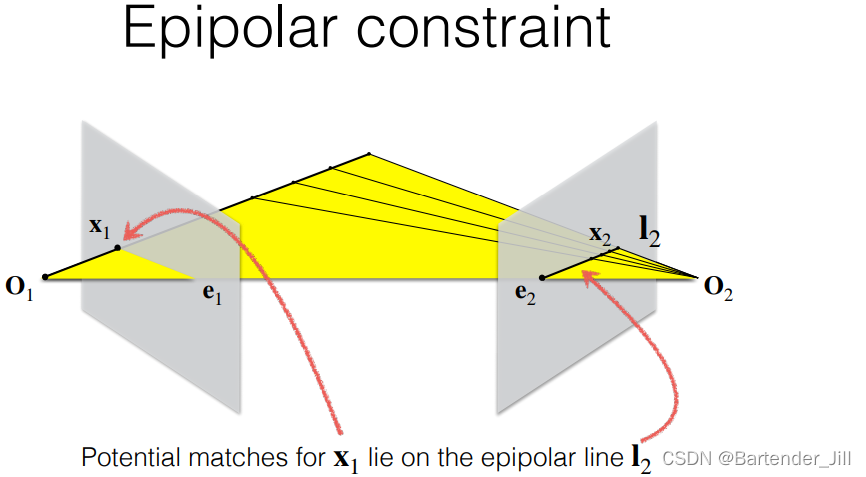
这一块可能比较绕，网上还有不少对极几何资料可供参考：

• 对极几何（Epipolar Geometry）基础及OpenCV实现
• SLAM基础-Epipolar Geometry、PnP、ICP
• 极线几何（Epipolar Geometry）

Q： 为什么要以 baseline 为底构造Epipolar Plane？
A： 因为两个相机可能处于不同高度，为了确保 候选点 能落在另一个相机的 一条直线 上，需要先构造出两个相机所在平面。

Q：为什么要让 候选点 落在另一个相机的 直线 上？这条 Epipolar Line 有什么意义？
A：意义很大，这限制了寻找对应点的搜索空间，提供了一定的约束条件，使立体匹配算法更加高效；Epipolar line 还描述了两个摄像机视图和它们捕捉的3D场景之间的关系，方便后续对齐。

为了更好地利用起Epipolar Geometry，我们还需要了解 基础矩阵 、本质矩阵 等概念以及相关数学推导。

二、 基础矩阵（Fundamental Matrix）

2.1 基础矩阵定义

为了理解基础矩阵，我们需要先理解 齐次坐标系下的直线性质。

假设现在有一条直线 ax + by + c = 0 ，我们将系数提取成 向量形式I：

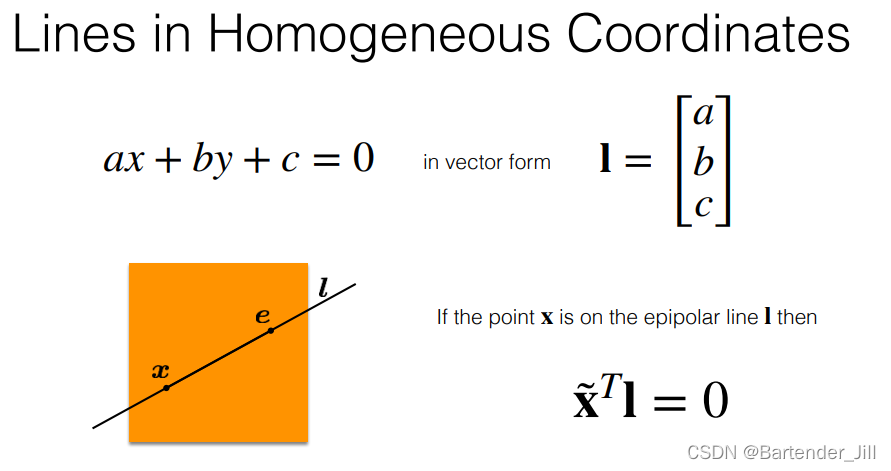
那我们可以发现一些 齐次坐标系 有趣的性质：

• 该直线上的点 点乘上 向量I 后，结果为0.
• 该直线外的点 点乘上 标准化的向量I 后，结果为点到该直线上的距离。
• 已知2维平面上两个不同的点的齐次坐标(x,y,1) 和 (x2,y2,1)，让这两个点作叉乘可以得到经过这两点的直线。

接下来，我们就要用这些性质进一步推导要讲的 基础矩阵 F ：

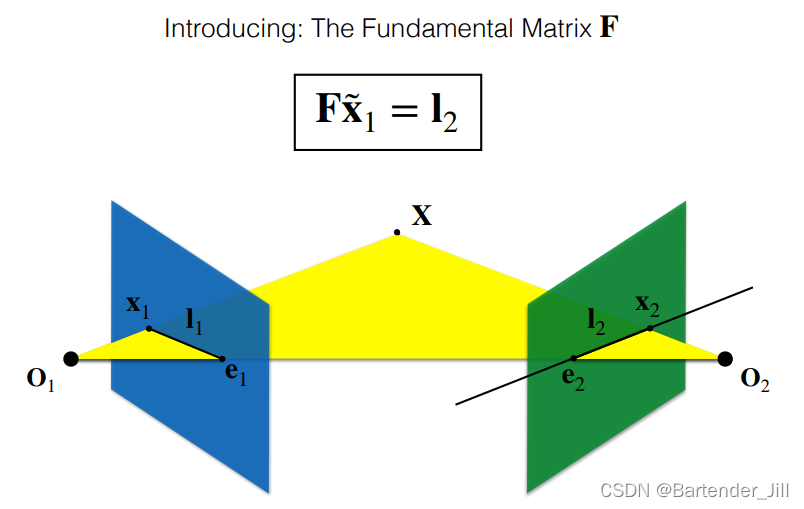
基础矩阵是什么？

1. 基础矩阵是一个 3x3 的矩阵，且encodes了整个 Epippolar Geometry 信息。（这里用英文是为了不丢失原意）
2. 给定 相机1上的一个点 x₁~，左乘上 基础矩阵F，则可以得到 相机2 的直线I₂。
3. 基础矩阵的含义是表达了相机2 对于 相机1的相对位置关系。

2.2 前置公式推导

我们不妨将上面说到的公式结合起来看：

已知：

• 基础矩阵F 乘 相机1上的某个像素点坐标 ，结果为相机2上的 候选点直线I₂。
• I₂直线上的任意一点x₂ 乘上 向量I₂ ，结果为 0。

两个式子结合起来，结果为0：

解：F * x1 = I2，然后 x2 * I2 = 0

我们虽然推导出了这个公式，但是我们还是不知道 ** F** 是什么，故这个公式现在还派不上用场，仍需要引入其他的定义。

假设 摄像机原点O 到 图像上的点x 的向量为$\bar{x}$ ，那么两个相机的 $\bar{x}$ 变换关系如下所示：

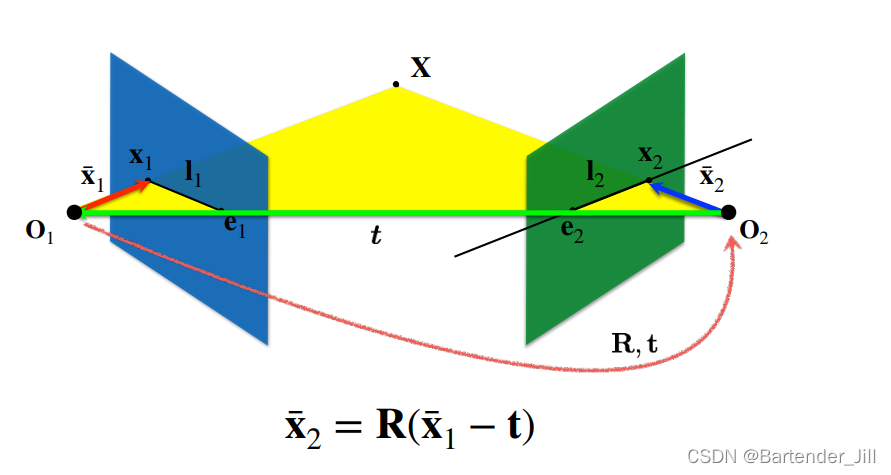
其中 t 是两相机之间距离， R 是旋转矩阵。(这里不懂的可以看 大白话推导三维重建[一] 的第三章摄像机外参部分)

而这两个向量可以由已知的相机像素坐标 $\tilde{x}$ 乘以内参矩阵的逆 K^-1 得到：

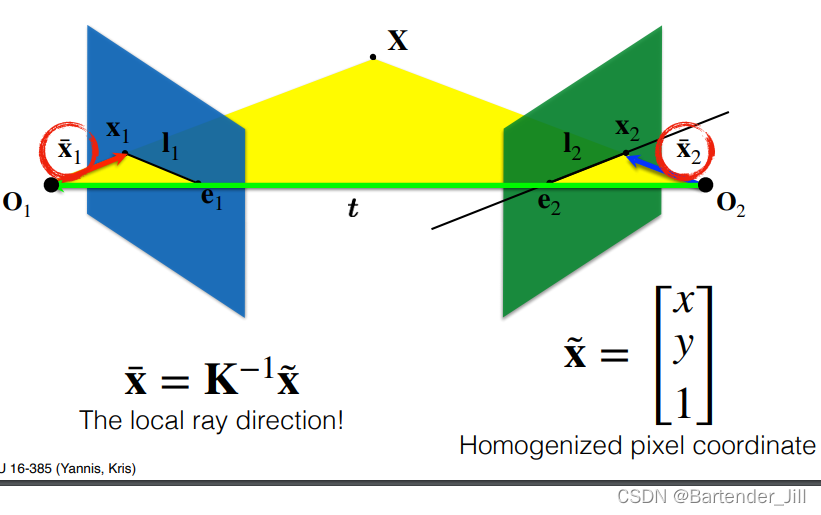
(这里不懂的可以看 大白话推导三维重建[一] 的第二章摄像机内参部分)

除此之外，由于这三个向量共面(coplanar)：

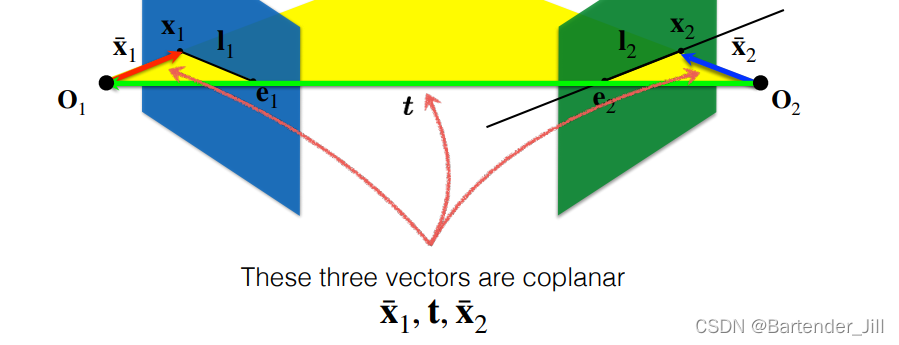
我们还能顺理成章推出以下两个公式 (不需要知道具体怎么算，利用叉乘点乘性质即可得到)：

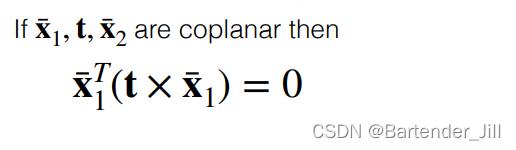
解：叉乘会得到一个垂直于平面的向量，两互相垂直向量点乘为0

且同理可得：

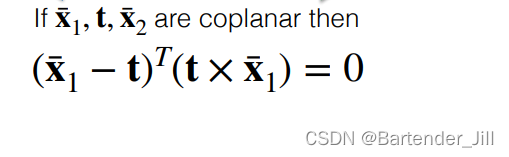
解：前一个括号得到的向量与后一个括号得到的向量互相垂直，两互相垂直向量点乘为0

2.3 基础矩阵公式推导

经过上述推导，我们手里已经有的条件有以下5个公式：

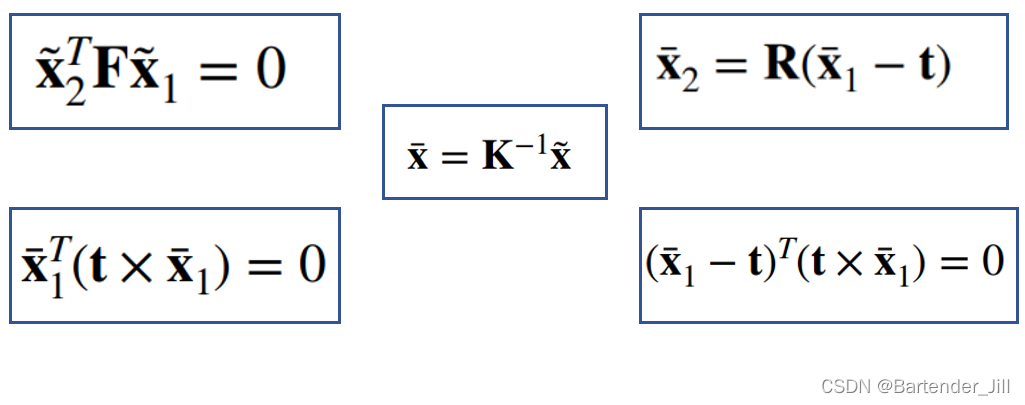
2.3.1 获取位移向量 [ t ] _x

把其中两个公式结合起来，可得：

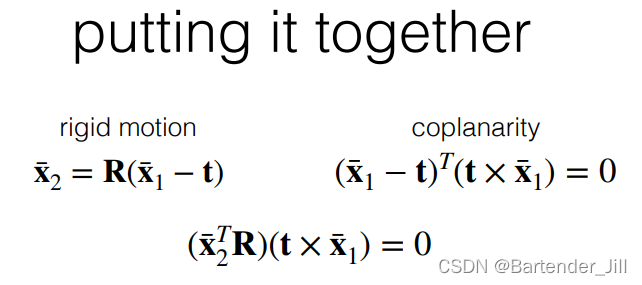
从而求解得到 baseline 的位移向量 t 的叉积化矩阵形式 ：

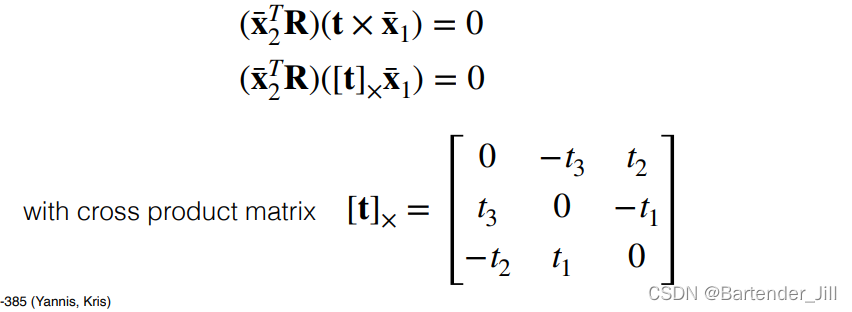
至于向量叉积如何写成矩阵形式 ：

(这里可以参考网上资料 CSDN：向量叉乘与叉乘矩阵 )

2.3.2 代入剩余公式

继续将其余三个公式代入，将向量方向 $\bar{x}$ 用已知的像素坐标 $\tilde{x}$ 表示：

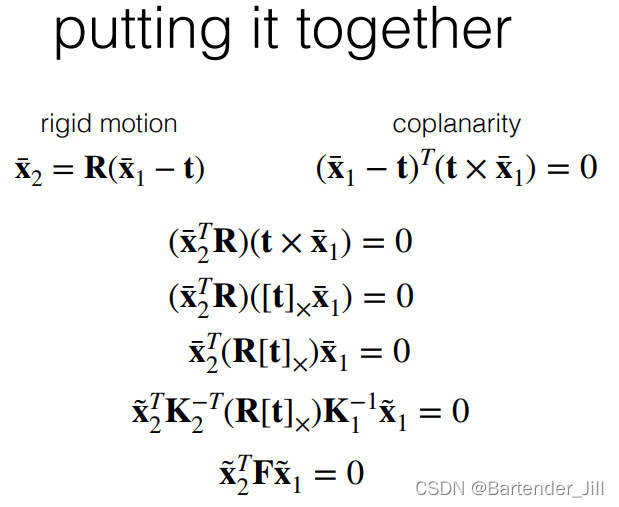
由上图可知，我们经过一轮推导，费尽周折，最后得到的就是这两个公式：

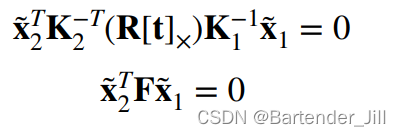
这两个公式联合起来看是不是有点眼熟？

基础矩阵F 不就正是中间那一大串吗：

这意味着什么？这意味着基础矩阵F包含了两个相机的内参信息(K₁ 和 K₂)、和相对位姿信息( R 和 t)。

所以我们可以得出结论：已知两个相机的内参矩阵 K₁、K₂，以及两个相机之间的旋转关系 R 和位移关系 t，可以求解基础矩阵F，以及相机1上的某个点所对应相机2的候选点直线 I₂：

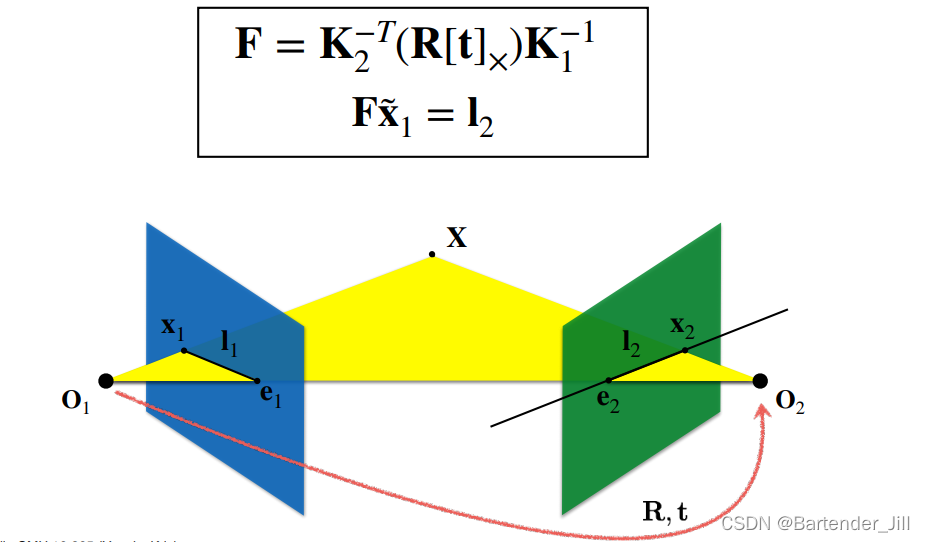
这个 基础矩阵F 是我们在已知两个相机内参和相对位姿等信息后推导出来的。

那么反过来想，在不知道两相机相对位姿的情况下，我们能否以某种其他的方式推导出这个基础矩阵F，从而恢复出这两个相机的相对位姿信息呢？

比如我们在用手机绕着客厅拍了一圈视频，我们能否仅根据这多视角的图片信息来恢复出不同相机之间的位姿关系，从而计算出3D空间中的点深度呢？答案是可以的。

求解相机相对位姿的算法有很多种，我这里只简单介绍一个较为经典的算法。

三、八点算法（The Eight-Point Algorithm）

八点算法(The Eight-Point Algorithm)就是一个利用 基本矩阵 得到一对相机之间的位姿关系的方法。顾名思义，其只需要八对特征点即可得到相机一相对于相机二的朝向信息等。

我们前面说过，基础矩阵F是一个3x3的矩阵，即有9个未知数F11~F33，$\tilde{x}$为相机1和相机2在3D空间同一点所对应的像素坐标：

因为点乘满足交换律，故我们不妨拆开来写成这种形式：

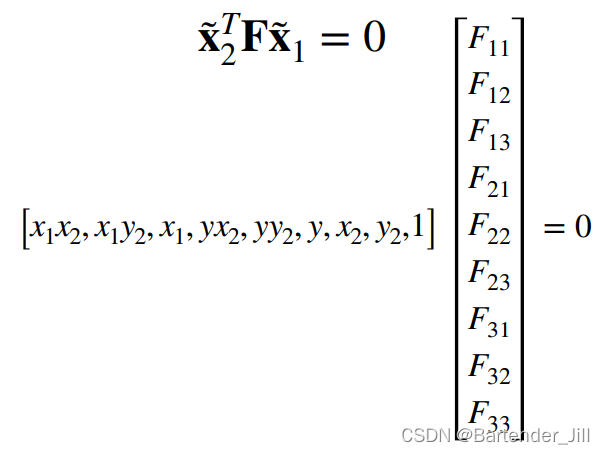
而要求解出F11-F33这九个参数，共需要 8 对特征点。(为什么是8对主要跟矩阵的秩有关，具体可以参考：CSDN：本质矩阵8点法中的线代知识)

求解的过程相当于求解一个齐次方程：

而齐次方程求解有很多种方式，如奇异值分解SVD等。

由于篇幅所限这里就不过多展开，详细解法可以看 Wikipedia：Eight-point algorithm。

四、补充知识：像素匹配

用RGB值来判断两张图片是否有对应像素显然行不通，比如图像上有一面白墙，那所墙上的点都没有区分度，并不能用于特征点匹配。

故现在用的特征点一般都包含了形状信息，即该像素值与周围像素的梯度变化情况作为特征，常用的特征点方法有：Harris 角点、SIFT等。匹配方法有RANSAC等：

总结

本篇文章主要讲解了对极几何的基本推导过程以及基础矩阵的作用，本人也是初学者，如有错误，欢迎指出。