- 1Caused by: java.lang.ClassNotFoundException: org.apache.hadoop.yarn.exceptions.YarnRuntimeException
- 2Ubuntu 20.04 安装RVM
- 3LLaMA: 高效且开源的基础语言模型
- 4网易+腾讯必问题库精选 C++经典编程面试题
- 5UE5 Lightmap使用
- 6[pyqt5][python][原创]pyqt5登陆界面跳转并关闭子窗口全部退出_pyqt5 关闭子窗口
- 72022年简历石沉大海,别投了,软件测试岗位饱和了...._软件测试投简历海投吗
- 8centos7安装cuda、dudnn、Nvidia驱动[最详细的教程和报错解决方案]_no package /root/libcudnn7-7.6.5.32-1.cuda10.0.x86
- 9QGIS插件开发详细教程
- 10Unity3d C# 实现滑动条(Slider)的拖拽开始和结束、点击等事件的拓展功能(含源码)_u3d slider点击拖拽弹出提示
三次样条插值原理及openCV实现三种边界条件(CSDN为数不多的正确版本)_三次样条边界条件
赞
踩
前情总结
同事在工作中遇到需要样条插值的情况,帮他找实现代码的时候想根据博客推一遍原理,结果发现大家的博客都是孪生兄弟,而且错的地方也都遗传了,所以推完过来水一篇博客。(能听出我跃跃欲试想说自己好单纯好不做作的意思吗?)
参考博客1
参考博客2
其实以上两位都很厉害,有些地方我也不算完全掌握,只是做了推导修正和c++代码实现,还优化了溢出的处理等等。
那这么看起来我也蛮厉害,那不谦虚了。
算法介绍及原理解析
写算法过程中会遇到一些需要插值的时候,我以前常用的是拟合,基本只能图个神似,很多时候拟合出来的曲线不过原来的点。插值会好很多,毕竟原来的正确点可以保留,而且能平滑预测未知点。
三次样条插值原理是分段插值,每段计算一个三次多项式。输入是你已知的一系列点,设其x坐标是
[
x
0
,
x
1
,
x
2
,
x
3
.
.
.
.
,
x
n
]
[x_{0},x_{1},x_{2},x_{3}....,x_{n}]
[x0,x1,x2,x3....,xn]
每个
x
i
x_{i}
xi都有对应的
y
i
y_{i}
yi。他们也把[
x
0
x_{0}
x0,
x
n
x_{n}
xn]这个区间分成了n段,我们现在就是要每段求解一个三次多项式。三次样条插值需要符合的条件如下:
- 在每个区间段[ x i , x i + 1 ] 上 , S i ( x ) x_{i},x_{i+1}]上,S_{i}(x) xi,xi+1]上,Si(x)都是一个三次方程
- 必须与已知点重合,即 S ( x i ) = y i ( i = 0 , 1 , . . . . , n ) S(x_{i})=y_{i} (i=0,1,....,n) S(xi)=yi(i=0,1,....,n)
- 曲线光滑,即 S ( x ) , S ′ ( x ) , S ′ ′ ( x ) S(x),S'(x),S''(x) S(x),S′(x),S′′(x)连续
每个三次方程形式如下
y
=
a
i
+
b
i
x
+
c
i
x
2
+
d
i
x
3
y=a_{i}+b_{i}x+c_{i}x^2+d_{i}x^3
y=ai+bix+cix2+dix3
这个方程称之为三次样条函数
S
i
(
x
)
S_{i}(x)
Si(x).
我前面需要求解的也就是每段的
a
i
,
b
i
,
c
i
,
d
i
a_{i},b_{i},c_{i},d_{i}
ai,bi,ci,di。
论证边界问题
我们要找出 4 n 4n 4n个方程来求解以上 4 ∗ n 4*n 4∗n个未知数
首先,由于所有点必须满足插值条件 S i ( x i ) = y i ( i = 0 , 1 , . . . . , n ) S_{i}(x_{i})=y_{i} (i=0,1,....,n) Si(xi)=yi(i=0,1,....,n) 及 S ( x ) S(x) S(x)连续。故除了两个端点,所有n-1个内部点的每个点都满足 S i ( x i + 1 ) = y i + 1 S_{i}(x_{i+1})=y_{i+1} Si(xi+1)=yi+1 , S i + 1 ( x i + 1 ) = y i + 1 S_{i+1}(x_{i+1})=y_{i+1} Si+1(xi+1)=yi+1 。
前后两个分段三次方程,则有2(n-1)个方程,再加上两个端点分别满足第一个和最后一个三次方程,则总共有2n个方程;
其次,n-1个内部点的一阶导数应该是连续的,即在第 i 区间的末点和第 i+1 区间的起点是同一个点,它们的一阶导数应该也相等,即 S i ′ ( x i + 1 ) = S i + 1 ′ ( x i + 1 ) S'_{i}(x_{i+1})=S'_{i+1}(x_{i+1}) Si′(xi+1)=Si+1′(xi+1) 则有n-1个方程
另外,内部点的二阶导数也要连续,即 S i ′ ′ ( x i + 1 ) = S i + 1 ′ ′ ( x i + 1 ) S''_{i}(x_{i+1})=S''_{i+1}(x_{i+1}) Si′′(xi+1)=Si+1′′(xi+1) ,也有n-1个方程
现在总共有4n-2个方程了,还差两个方程就可以解出所有未知数了,这两个方程我们通过边界条件得到。
边界条件介绍
-
自然边界 ( Natural Spline ):指定端点二阶导数为0, S 0 ′ ′ ( x 0 ) = S n − 1 ′ ′ ( x n ) = 0 S''_{0}(x_{0})=S''_{n-1}(x_{n})=0 S0′′(x0)=Sn−1′′(xn)=0
-
固定边界 ( Clamped Spline ): 指定端点一阶导数,这里分别定为A和B。即 S 0 ′ ′ ( x 0 ) = A , S n − 1 ′ ′ ( x n ) = B S''_{0}(x_{0})=A,S''_{n-1}(x_{n})=B S0′′(x0)=A,Sn−1′′(xn)=B
-
非扭结边界( Not-A-Knot Spline ): 使两端点的三阶导与这两端点的邻近点的三阶导相等,即
S 0 ′ ′ ′ ( x 0 ) = S 1 ′ ′ ′ ( x 1 ) S'''_{0}(x_{0})= S'''_{1}(x_{1}) S0′′′(x0)=S1′′′(x1) and S n − 2 ′ ′ ′ ( x n − 1 ) = S n − 1 ′ ′ ′ ( x n ) S'''_{n-2}(x_{n-1})= S'''_{n-1}(x_{n}) Sn−2′′′(xn−1)=Sn−1′′′(xn)
很多博客中对这三种边界条件介绍不多,我理解的就是自然边界使端点处尽量不设限制,让最后段落斜率保持不变;固定边界表示你可以指定两端斜率,这个在后面的推导中很多博客都错了(公式错误);非扭结边界我大概猜测是让两边不扭转,其实还不是很清楚。
公式推导
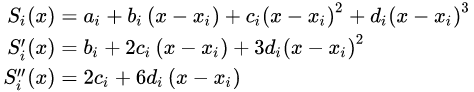
-
根据 S i ( x i ) = y i S_{i}(x_{i})=y_{i} Si(xi)=yi,结合上面公式1,可得
a i = y i a_{i}=y_{i} ai=yi -
用 h i = x i + 1 − x i h_{i}=x_{i+1}-x_{i} hi=xi+1−xi来表示第i步的步长,由 S i ( x i + 1 ) = y i + 1 S_{i}(x_{i+1})=y_{i+1} Si(xi+1)=yi+1可得
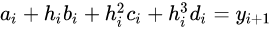
-
由 S i ′ ′ ( x i + 1 ) = S i + 1 ′ ′ ( x i + 1 ) S''_{i}(x_{i+1})= S''_{i+1}(x_{i+1}) Si′′(xi+1)=Si+1′′(xi+1),得 2 c i + 6 h i d i = 2 c i + 1 2c_{i}+6h_{i}d{i}=2c_{i+1} 2ci+6hidi=2ci+1
设 m i = S i ′ ′ ( x i ) = 2 c i m_{i}=S''_{i}(x_{i})=2c_{i} mi=Si′′(xi)=2ci,则上式可改写为 m i + 6 h i d i = m i + 1 m_{i}+6h_{i}d_{i}=m_{i+1} mi+6hidi=mi+1
可得
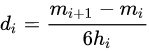
-
然后将 a i , c i , d i a_{i},c_{i},d_{i} ai,ci,di代入2中的公式。可推导出
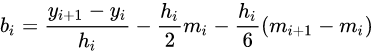
-
由 S i ′ ( x i + 1 ) = S i + 1 ′ ( x i + 1 ) S'_{i}(x_{i+1})= S'_{i+1}(x_{i+1}) Si′(xi+1)=Si+1′(xi+1)推出
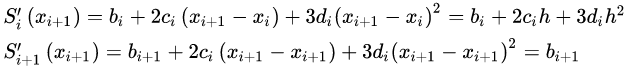
可得到
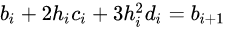
-
再将 a i , b i , c i , d i a_{i},b_{i},c_{i},d_{i} ai,bi,ci,di代入5中公式,可得
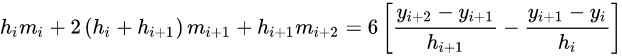
这样我们就可以得到关于m的线性方程组,其余h和y都已知。
方程组
1.自然边界( Natural Spline )
由于自然边界条件下
S
0
′
′
(
x
0
)
=
S
n
−
1
′
′
(
x
n
)
=
0
S''_{0}(x_{0})=S''_{n-1}(x_{n})=0
S0′′(x0)=Sn−1′′(xn)=0,则求解方程组如下,该方程下
m
0
,
m
n
m_{0},m_{n}
m0,mn都为0.

2.夹持边界( Clamped Spline )
首尾处端点的一阶微分是被指定的,可以假设为A和B,可推
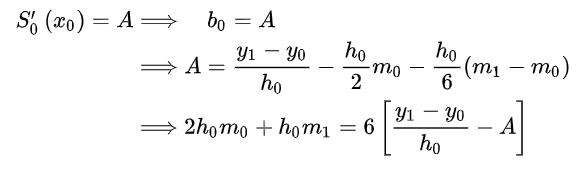
这个普遍博客中是没问题的,但是下一步就出现了问题了。
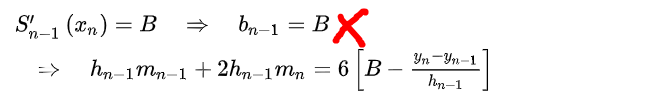
其实也不能说全错,中间那步错了,结果对了,这不是尴尬嘛,应该是
b
n
−
1
+
m
n
−
1
∗
h
i
−
1
+
3
∗
(
m
i
−
m
i
−
1
)
/
(
6
∗
h
i
−
1
)
∗
h
i
−
1
2
=
B
b_{n-1}+m_{n-1}*h_{i-1}+3*(m_{i}-m_{i-1})/(6*h_{i-1})*h_{i-1}^2=B
bn−1+mn−1∗hi−1+3∗(mi−mi−1)/(6∗hi−1)∗hi−12=B
然后就是后面那个结果了,我已经推过了,我猜测是原博主不小心写错,然后大家都错了[doge]
还一个错误是,这一步已经推出等号右边的公式首尾不是0了,和其他的是不同,但是没什么人特别说明,给人一种右侧的矩阵没变的感觉。
左侧为
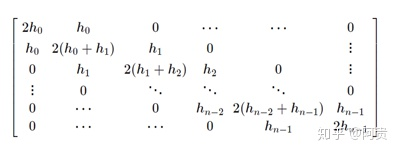
右侧第一项为
[
y
1
−
y
0
h
0
−
A
]
[\frac{y_{1}-y_{0}}{h_{0}}-A]
[h0y1−y0−A],最后一项是
[
B
−
y
n
−
y
n
−
1
h
n
−
1
]
[B-\frac{y_{n}-y_{n-1}}{h_{n-1}}]
[B−hn−1yn−yn−1]
3.非扭结边界
写到这里我有点累了,而且我本身对这个也没推的特别仔细,所以我还是复制粘贴一下好。

算法步骤
1.根据输入点计算步长和y的一阶差分
2.根据y值计算a,再根据求解矩阵求得c。
3.已知m,h, y求b,d
4.在根据输入的一系列float表示的x值,输出对应的y值,这个y值就是插值结果
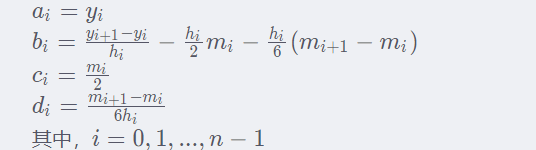
贴上一个复制来的图片,辅助一下同学们理解。
代码实现

大致效果如图,三种边界对应颜色分别是BGR。
void BSplineNatural(vector<Point2f> input_points, vector<float> input_x, vector<float>& predicted_y) { // input_points: 输入点集,根据这个计算插值 // input_x: 输入x值,计算得到各多项式系数后,根据这个输出预测值 //三次线性插值主要就是为了求各段的三次多项式,即每段的a b c d. predicted_y.clear(); int n = input_points.size(); if (n < 3) { return; } Mat a = Mat::zeros(n-1, 1, CV_32FC1); Mat b = Mat::zeros(n-1, 1, CV_32FC1); Mat d = Mat::zeros(n-1, 1, CV_32FC1); Mat dx = Mat::zeros(n - 1, 1, CV_32FC1); Mat dy = Mat::zeros(n - 1, 1, CV_32FC1); for (int i = 0; i < input_points.size() - 1; i++) { //计算a和x,y的一阶差分 a.at<float>(i, 0) = input_points[i].y; dx.at<float>(i, 0) = (input_points[i + 1].x - input_points[i].x); dy.at<float>(i, 0) = (input_points[i + 1].y - input_points[i].y); } //A为求解方程组的左侧矩阵,B为右侧 Mat A = Mat::zeros(n, n, CV_32FC1); Mat B = Mat::zeros(n, 1, CV_32FC1); //设置关于端点的部分 A.at<float>(0, 0) = 1; A.at<float>(n - 1, n - 1) = 1; for (int i = 1; i <= n - 2; i++) { A.at<float>(i, i - 1) = dx.at<float>(i - 1, 0); A.at<float>(i, i) = 2 * (dx.at<float>(i - 1, 0) + dx.at<float>(i, 0)); A.at<float>(i, i + 1) = dx.at<float>(i, 0); B.at<float>(i, 0) = 3 * (dy.at<float>(i, 0) / dx.at<float>(i, 0) - dy.at<float>(i - 1, 0) / dx.at<float>(i - 1, 0)); } Mat c = A.inv()*B; std::cout<< "Natural S''(0):" << setprecision(2) << fixed << c.at<float>(0,0) << std::endl; std::cout <<"Natural S''(n-1):" << setprecision(2) << fixed << c.at<float>(n-1, 0) << std::endl; for (int i = 0; i <= n - 2; i++) { d.at<float>(i, 0) = (c.at<float>(i + 1, 0) - c.at<float>(i, 0)) / (3 * dx.at<float>(i, 0)); b.at<float>(i, 0) = dy.at<float>(i, 0) / dx.at<float>(i, 0) - dx.at<float>(i, 0) *(2 * c.at<float>(i, 0) + c.at<float>(i + 1, 0)) / 3; } for (int i = 0; i < input_x.size(); i++) { int j = 0; for (int ii = 0; ii <= n - 2; ii++) { if (input_x[i] >= input_points[ii].x && input_x[i] < input_points[ii + 1].x) { j = ii; break; } else if (input_x[i] >= input_points[n - 1].x) { j = n - 2; } } float middleV = a.at<float>(j, 0) + b.at<float>(j, 0)* (input_x[i] - input_points[j].x) + c.at<float>(j, 0)*(input_x[i] - input_points[j].x)* (input_x[i] - input_points[j].x) + d.at<float>(j, 0)*(input_x[i] - input_points[j].x)* (input_x[i] - input_points[j].x)*(input_x[i] - input_points[j].x); predicted_y.push_back(middleV); } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
void BSplineClamped(vector<Point2f> input_points, vector<float> input_x, vector<float>& predicted_y) { // input_points: 输入点集,根据这个计算插值 // input_x: 输入x值,计算得到各多项式系数后,根据这个输出预测值 //三次线性插值主要就是为了求各段的三次多项式,即每段的a b c d. double k_start = -0.3; double k_end = 0.45; predicted_y.clear(); int n = input_points.size(); if (n < 3) { return; } Mat a = Mat::zeros(n - 1, 1, CV_32FC1); Mat b = Mat::zeros(n - 1, 1, CV_32FC1); Mat d = Mat::zeros(n - 1, 1, CV_32FC1); Mat dx = Mat::zeros(n - 1, 1, CV_32FC1); Mat dy = Mat::zeros(n - 1, 1, CV_32FC1); for (int i = 0; i < input_points.size() - 1; i++) { //计算a和x,y的一阶差分 a.at<float>(i, 0) = input_points[i].y; dx.at<float>(i, 0) = (input_points[i + 1].x - input_points[i].x); dy.at<float>(i, 0) = (input_points[i + 1].y - input_points[i].y); } //A为求解方程组的左侧矩阵,B为右侧 Mat A = Mat::zeros(n, n, CV_32FC1); Mat B = Mat::zeros(n, 1, CV_32FC1); //设置关于端点的部分 A.at<float>(0, 0) = 2*dx.at<float>(0, 0); A.at<float>(0, 1) = dx.at<float>(0, 0); A.at<float>(n - 1, n - 1) = 2*dx.at<float>(n-2, 0); A.at<float>(n - 1, n - 2) = dx.at<float>(n-2, 0); B.at<float>(0, 0) = 3*(dy.at<float>(0, 0) / dx.at<float>(0, 0) - k_start); B.at<float>(n-1, 0) = 3*(k_end - dy.at<float>(n-2, 0) / dx.at<float>(n-2, 0)); for (int i = 1; i <= n - 2; i++) { A.at<float>(i, i - 1) = dx.at<float>(i - 1, 0); A.at<float>(i, i) = 2 * (dx.at<float>(i - 1, 0) + dx.at<float>(i, 0)); A.at<float>(i, i + 1) = dx.at<float>(i, 0); B.at<float>(i, 0) = 3 * (dy.at<float>(i, 0) / dx.at<float>(i, 0) - dy.at<float>(i - 1, 0) / dx.at<float>(i - 1, 0)); } Mat c = A.inv()*B; for (int i = 0; i <= n - 2; i++) { d.at<float>(i, 0) = (c.at<float>(i + 1, 0) - c.at<float>(i, 0)) / (3 * dx.at<float>(i, 0)); b.at<float>(i, 0) = dy.at<float>(i, 0) / dx.at<float>(i, 0) - dx.at<float>(i, 0) *(2 * c.at<float>(i, 0) + c.at<float>(i + 1, 0)) / 3; } std::cout << "Natural S'(0)=k_start=:" << setprecision(2) << fixed << b.at<float>(0, 0) << std::endl; std::cout << "Natural S'(n-1)=k_end=:" << setprecision(2) << fixed << b.at<float>(n - 2, 0)+ 2*c.at<float>(n-2)*dx.at<float>(n-2,0)+3* d.at<float>(n - 2)* dx.at<float>(n - 2, 0)*dx.at<float>(n - 2, 0) << std::endl; for (int i = 0; i < input_x.size(); i++) { int j = 0; for (int ii = 0; ii <= n - 2; ii++) { if (input_x[i] >= input_points[ii].x && input_x[i] < input_points[ii + 1].x) { j = ii; break; } else if (input_x[i] >= input_points[n - 1].x) { j = n - 2; } } float middleV = a.at<float>(j, 0) + b.at<float>(j, 0)* (input_x[i] - input_points[j].x) + c.at<float>(j, 0)*(input_x[i] - input_points[j].x)* (input_x[i] - input_points[j].x) + d.at<float>(j, 0)*(input_x[i] - input_points[j].x)* (input_x[i] - input_points[j].x)*(input_x[i] - input_points[j].x); predicted_y.push_back(middleV); } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
void BSplineNotAKnot(vector<Point2f> input_points, vector<float> input_x, vector<float>& predicted_y) { // input_points: 输入点集,根据这个计算插值 // input_x: 输入x值,计算得到各多项式系数后,根据这个输出预测值 //三次线性插值主要就是为了求各段的三次多项式,即每段的a b c d. predicted_y.clear(); int n = input_points.size(); if (n < 3) { return; } Mat a = Mat::zeros(n - 1, 1, CV_32FC1); Mat b = Mat::zeros(n - 1, 1, CV_32FC1); Mat d = Mat::zeros(n - 1, 1, CV_32FC1); Mat dx = Mat::zeros(n - 1, 1, CV_32FC1); Mat dy = Mat::zeros(n - 1, 1, CV_32FC1); for (int i = 0; i < input_points.size() - 1; i++) { //计算a和x,y的一阶差分 a.at<float>(i, 0) = input_points[i].y; dx.at<float>(i, 0) = (input_points[i + 1].x - input_points[i].x); dy.at<float>(i, 0) = (input_points[i + 1].y - input_points[i].y); } //A为求解方程组的左侧矩阵,B为右侧 Mat A = Mat::zeros(n, n, CV_32FC1); Mat B = Mat::zeros(n, 1, CV_32FC1); //设置关于端点的部分 A.at<float>(0, 0) = -dx.at<float>(1, 0); A.at<float>(0, 1) = dx.at<float>(0, 0) + dx.at<float>(1, 0); A.at<float>(0, 2) = -dx.at<float>(0, 0); A.at<float>(n - 1, n - 1) = - dx.at<float>(n - 3, 0); A.at<float>(n - 1, n - 2) = dx.at<float>(n-3, 0) + dx.at<float>(n-2, 0); A.at<float>(n - 1, n - 3) = -dx.at<float>(n - 2, 0); for (int i = 1; i <= n - 2; i++) { A.at<float>(i, i - 1) = dx.at<float>(i - 1, 0); A.at<float>(i, i) = 2 * (dx.at<float>(i - 1, 0) + dx.at<float>(i, 0)); A.at<float>(i, i + 1) = dx.at<float>(i, 0); B.at<float>(i, 0) = 3 * (dy.at<float>(i, 0) / dx.at<float>(i, 0) - dy.at<float>(i - 1, 0) / dx.at<float>(i - 1, 0)); } Mat c = A.inv()*B; for (int i = 0; i <= n - 2; i++) { d.at<float>(i, 0) = (c.at<float>(i + 1, 0) - c.at<float>(i, 0)) / (3 * dx.at<float>(i, 0)); b.at<float>(i, 0) = dy.at<float>(i, 0) / dx.at<float>(i, 0) - dx.at<float>(i, 0) *(2 * c.at<float>(i, 0) + c.at<float>(i + 1, 0)) / 3; } for (int i = 0; i < input_x.size(); i++) { int j = 0; for (int ii = 0; ii <= n - 2; ii++) { if (input_x[i] >= input_points[ii].x && input_x[i] < input_points[ii + 1].x) { j = ii; break; } else if (input_x[i] >= input_points[n - 1].x) { j = n - 2; } } float middleV = a.at<float>(j, 0) + b.at<float>(j, 0)* (input_x[i] - input_points[j].x) + c.at<float>(j, 0)*(input_x[i] - input_points[j].x)* (input_x[i] - input_points[j].x) + d.at<float>(j, 0)*(input_x[i] - input_points[j].x)* (input_x[i] - input_points[j].x)*(input_x[i] - input_points[j].x); predicted_y.push_back(middleV); } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
前两个函数有输出首尾端点的二阶导数或者一阶导数,能看出来是符合定义的。



