- 1基于Spring Boot的智能化健身房管理平台
- 2STM32:两种方式实现超声波测距_stm32超声波测距
- 3入行网络安全需要学习哪些知识点?白帽子都给你汇总在这里,一文全懂_网络安全要学的内容
- 4小程序自定义组件扩展功能介绍_网站小程序扩展组件
- 5开源社区驱动高速演进,1Panel发布首个LTS版本_1panel是什么时候开始的
- 6Flutter开发之——IOS通信MethodChannel_ios fluttermethodchannel flutterbinarymessenger
- 7flink-sql所有语法详解-1.14_flinksql 博客文档
- 8Java中各个版本JDK分别有哪些常见的垃圾回收算法?它们的适用场景和开启方法是什么?_jdk17默认垃圾回收器
- 9内网渗透实战——红日ATT&CK系列靶场(一)学习笔记_红日靶场1攻略
- 10华为OD机试真题-CPU算力分配_cpu算力分配华为
第十三届蓝桥杯国赛真题 Java C 组【原卷】
赞
踩
发现宝藏
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。【宝藏入口】。
【考生须知】
考试开始后, 选手首先下载题目, 并使用考场现场公布的解压密码解压试题。
考试时间为 4 小时。考试期间选手可浏览自己已经提交的答案, 被浏览的答案允许拷贝。时间截止后,将无法继续提交或浏览答案。
对同一题目, 选手可多次提交答案, 以最后一次提交的答案为准。
选手必须通过浏览器方式提交自己的答案。选手在其它位置的作答或其它方式提交的答案无效。
试题包含 “结果填空” 和 “程序设计” 两种题型。
结果填空题: 要求选手根据题目描述直接填写结果。求解方式不限。不要求源代码。把结果填空的答案直接通过网页提交即可, 不要书写多余的内容。
程序设计题: 要求选手设计的程序对于给定的输入能给出正确的输出结果。考生的程序只有能运行出正确结果才有机会得分。
注意: 在评卷时使用的输入数据与试卷中给出的示例数据可能是不同的。选手的程序必须是通用的, 不能只对试卷中给定的数据有效。
所有源码必须在同一文件中。调试通过后,拷贝提交。
注意: 不要使用 package 语句。
注意:选手代码的主类名必须为: Main, 否则会被判为无效代码。
注意: 如果程序中引用了类库, 在提交时必须将 import 语句与程序的其他部分同时提交。只允许使用 Java 自带的类库。
试题 A: 斐波那契与 7
本题总分: 5 分
【问题描述】
斐波那契数列的递推公式为: F n = F n − 1 + F n − 2 F_{n}=F_{n-1}+F_{n-2} Fn=Fn−1+Fn−2, 其中 F 1 = F 2 = 1 F_{1}=F_{2}=1 F1=F2=1 。
请问, 斐波那契数列的第 1 至 202202011200 项(含)中, 有多少项的个位是 7 。
【答案提交】
这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。
试题 B: 小蓝做实验
本题总分:5 分
【问题描述】
小蓝很喜欢科研, 他最近做了一个实验得到了一批实验数据, 一共是两百万个正整数。如果按照预期, 所有的实验数据 x x x 都应该满足 1 0 7 ≤ x ≤ 1 0 8 10^{7} \leq x \leq 10^{8} 107≤x≤108 。但是做实验都会有一些误差, 会导致出现一些预期外的数据, 这种误差数据 y y y 的范围是 1 0 3 ≤ y ≤ 1 0 12 10^{3} \leq y \leq 10^{12} 103≤y≤1012 。由于小蓝做实验很可靠, 所以他所有的实验数据中 99.99 % 99.99 \% 99.99% 以上都是符合预期的。小蓝的所有实验数据都在 primes.txt 中, 现在他想统计这两百万个正整数中有多少个是质数, 你能告诉他吗?
【答案提交】
这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。
试题 C: 取模
时间限制: 3.0 s 3.0 \mathrm{~s} 3.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 10 分
【问题描述】
给定 n , m n, m n,m, 问是否存在两个不同的数 x , y x, y x,y 使得 1 ≤ x < y ≤ m 1 \leq x<y \leq m 1≤x<y≤m 且 n m o d x = n \bmod x= nmodx= n m o d y n \bmod y nmody 。
【输入格式】
输入包含多组独立的询问。
第一行包含一个整数 T T T 表示询问的组数。
接下来 T T T 行每行包含两个整数 n , m n, m n,m, 用一个空格分隔, 表示一组询问。
【输出格式】
输出 T T T 行, 每行依次对应一组询问的结果。如果存在, 输出单词 Yes; 如果不存在, 输出单词 No。
【样例输入】
3 3 3
5 2 52 52
99 9 999 999
【样例输出】
N o No No
N o No No
Y e s Yes Yes
【评测用例规模与约定】
对于 20 % 20 \% 20% 的评测用例, T ≤ 100 , n , m ≤ 1000 T \leq 100, n, m \leq 1000 T≤100,n,m≤1000;
对于 50 % 50 \% 50% 的评测用例, T ≤ 10000 , n , m ≤ 1 0 5 T \leq 10000, n, m \leq 10^{5} T≤10000,n,m≤105;
对于所有评测用例, 1 ≤ T ≤ 1 0 5 , 1 ≤ n ≤ 1 0 9 , 2 ≤ m ≤ 1 0 9 1 \leq T \leq 10^{5}, 1 \leq n \leq 10^{9}, 2 \leq m \leq 10^{9} 1≤T≤105,1≤n≤109,2≤m≤109 。
试题 D: 内存空间
时间限制: 3.0 s 3.0 \mathrm{~s} 3.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 10 分
【问题描述】
小蓝最近总喜欢计算自己的代码中定义的变量占用了多少内存空间。
为了简化问题, 变量的类型只有以下三种:
int: 整型变量, 一个 int 型变量占用 4 Byte 的内存空间。
long:长整型变量, 一个 long 型变量占用 8 Byte 的内存空间。
String: 字符串变量, 占用空间和字符串长度有关, 设字符串长度为 L L L,则字符串占用 L L L Byte 的内存空间, 如果字符串长度为 0 则占用 0 Byte 的内存空间。
定义变量的语句只有两种形式, 第一种形式为:
type var1=value1, var2=value2…;
定义了若干个 type 类型变量 var1、var2、开, 并且用 value1、value2 …初始化,
多个变量之间用’, ‘分隔, 语句以’; '结尾, type 可能是 int、long 或 String。例如 int a = 1 , b = 5 , c = 6 a=1, b=5, c=6 a=1,b=5,c=6; 占用空间为 12 Byte; long a = 1 , b = 5 a=1, b=5 a=1,b=5;占用空间为 16 Byte; String s 1 = s 1= s1= " ", s2=“hello”, s3=“world”;占用空间为 10 Byte。
第二种形式为:
type[] arr1=new type[size1], arr2=new type[size2] ⋯ \cdots ⋯;
定义了若干 type 类型的一维数组变量 arr 1 , arr 2 ⋯ \operatorname{arr} 1, \operatorname{arr} 2 \cdots arr1,arr2⋯, 且数组的大小为 size1、size2 是, 多个变量之间用’, ‘进行分隔, 语句以’;’ 结尾, type 只可能是 int 或 long。例如 int [] al=new int[10]; 占用的内存空间为 40
Byte; long[] a1=new long[10],a2=new long[10];占用的内存空间为 160 Byte.
已知小蓝有 T T T 条定义变量的语句, 请你帮他统计下一共占用了多少内存空间。结果的表示方式为: a G B b M B c K B d B a \mathrm{~GB} b \mathrm{MB} c \mathrm{~KB} d \mathrm{~B} a GBbMBc KBd B, 其中 a 、 b 、 c 、 d a 、 b 、 c 、 d a、b、c、d 为统计的结果, GB、MB、KB、B 为单位。优先用大的单位来表示, 1 G B = 1024 M B 1 \mathrm{~GB}=1024 \mathrm{MB} 1 GB=1024MB, 1 M B = 1024 K B , 1 K B = 1024 B 1 \mathrm{MB}=1024 \mathrm{~KB}, 1 \mathrm{~KB}=1024 \mathrm{~B} 1MB=1024 KB,1 KB=1024 B, 其中 B 表示 Byte。如果 a 、 b 、 c 、 d a 、 b 、 c 、 d a、b、c、d 中的某几个数字为 0 , 那么不必输出这几个数字及其单位。题目保证一行中只有一句定义变量的语句, 且每条语句都满足题干中描述的定义格式, 所有的变量名都是合法的且均不重复。题目中的数据很规整, 和上述给出的例子类似, 除了类型后面有一个空格, 以及定义数组时 new 后面的一个空格之外, 不会出现多余的空格。
【输入格式】
输入的第一行包含一个整数 T T T, 表示有 T T T 句变量定义的语句。
接下来 T T T 行, 每行包含一句变量定义语句。
【输出格式】
输出一行包含一个字符串, 表示所有语句所占用空间的总大小。
【样例输入 1】
1
long [ ] nums=new long [131072];
【样例输出 1】
1 M B 1 \mathrm{MB} 1MB
【样例输入 2】
4
int a = 0 , b = 0 a=0, b=0 a=0,b=0;
long x = 0 , y = 0 x=0, y=0 x=0,y=0
String s 1 = \mathrm{s} 1= s1= “hello”, s 2 = \mathrm{s} 2= s2= “world”;
long[ ] arr1=new long[100000], arr2=new long[100000];
【样例输出 2】
1 MB538KB546B
【样例说明】
样例 1 , 占用的空间为 131072 × 8 = 1048576 B 131072 \times 8=1048576 \mathrm{~B} 131072×8=1048576 B, 换算过后正好是 1 M B 1 \mathrm{MB} 1MB, 其它三个单位 G B 、 K B 、 B \mathrm{GB} 、 \mathrm{~KB} 、 \mathrm{~B} GB、 KB、 B 前面的数字都为 0 , 所以不用输出。
样例 2 , 占用的空间为 4 × 2 + 8 × 2 + 10 + 8 × 100000 × 2 B 4 \times 2+8 \times 2+10+8 \times 100000 \times 2 \mathrm{~B} 4×2+8×2+10+8×100000×2 B, 换算后是 1MB538K5546B。
【评测用例规模与约定】
对于所有评测用例, 1 ≤ T ≤ 10 1 \leq T \leq 10 1≤T≤10, 每条变量定义语句的长度不会超过 1000 - 所有的变量名称长度不会超过 10 , 且都由小写字母和数字组成。对于整型变量, 初始化的值均是在其表示范围内的十进制整数, 初始化的值不会是变量.对于 String 类型的变量, 初始化的内容长度不会超过 50 , 且内容仅包含小写字母和数字, 初始化的值不会是变量. 对于数组类型变量, 数组的长度为一个整数, 范围为: [ 0 , 2 30 ] \left[0,2^{30}\right] [0,230], 数组的长度不会是变量。 T T T 条语句定义的变量所占的内存空间总大小不会超过 1 G B 1 \mathrm{~GB} 1 GB, 且大于 0 B 0 \mathrm{~B} 0 B 。
试题 E \mathrm{E} E : 斐波那契数组
时间限制: 3.0 s 3.0 \mathrm{~s} 3.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 15 分
【问题描述】
如果数组 A = ( a 0 , a 1 , ⋯ , a n − 1 ) A=\left(a_{0}, a_{1}, \cdots, a_{n-1}\right) A=(a0,a1,⋯,an−1) 满足以下条件, 就说它是一个斐波那契数组:
- n ≥ 2 n \geq 2 n≥2;
- a 0 = a 1 a_{0}=a_{1} a0=a1;
- 对于所有的 i ( i ≥ 2 ) i(i \geq 2) i(i≥2), 都满足 a i = a i − 1 + a i − 2 a_{i}=a_{i-1}+a_{i-2} ai=ai−1+ai−2 。
现在, 给出一个数组 A A A, 你可以执行任意次修改, 每次修改将数组中的某个位置的元素修改为一个大于 0 的整数。请问最少修改几个元素之后, 数组 A A A会变成一个斐波那契数组。
【输入格式】
输入的第一行包含一个整数 n n n, 表示数组 A A A 中的元素个数。
第二行包含 n n n 个整数 a 0 , a 1 , ⋯ , a n − 1 a_{0}, a_{1}, \cdots, a_{n-1} a0,a1,⋯,an−1, 相邻两个整数之间用一个空格分隔。
【输出格式】
输出一行包含一个整数表示最少需要修改数组 A A A 中的几个元素之后, 数组 A A A 可以变为一个斐波那契数组。
【样例输入】
5 5 5
1 2 4 4 8 12448 12448
【样例输出】
3 3 3
【样例说明】
将原数组修改为 ( 1 , 1 , 2 , 3 , 5 ) (1,1,2,3,5) (1,1,2,3,5), 最少修改三个元素变成了一个斐波那契数组。
【评测用例规模与约定】
对于所有评测用例, 2 ≤ n ≤ 1 0 5 , 1 ≤ a i ≤ 1 0 6 2 \leq n \leq 10^{5}, 1 \leq a_{i} \leq 10^{6} 2≤n≤105,1≤ai≤106 。
试题 F: 最大公约数
时间限制: 3.0 s 3.0 \mathrm{~s} 3.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 15 分
【问题描述】
给定一个数组, 每次操作可以选择数组中任意两个相邻的元素 x , y x, y x,y 并将其中的一个元素替换为 gcd ( x , y ) \operatorname{gcd}(x, y) gcd(x,y), 其中 gcd ( x , y ) \operatorname{gcd}(x, y) gcd(x,y) 表示 x x x 和 y y y 的最大公约数。
请问最少需要多少次操作才能让整个数组只含 1 。
【输入格式】
输入的第一行包含一个整数 n n n, 表示数组长度。
第二行包含 n n n 个整数 a 1 , a 2 , ⋯ , a n a_{1}, a_{2}, \cdots, a_{n} a1,a2,⋯,an, 相邻两个整数之间用一个空格分隍。
【输出格式】
输出一行包含一个整数, 表示最少操作次数。如果无论怎么操作都无法满足要求, 输出 -1 。
【样例输入】
2 2 2
4 6 9 469 469
【样例输出】
4 4 4
【评测用例规模与约定】
对于 30 % 30 \% 30% 的评测用例, n ≤ 500 , a i ≤ 1000 n \leq 500, a_{i} \leq 1000 n≤500,ai≤1000 ,
对于 50 % 50 \% 50% 的评测用例, n ≤ 5000 , a i ≤ 1 0 6 n \leq 5000, a_{i} \leq 10^{6} n≤5000,ai≤106;
对于所有评测用例, 1 ≤ n ≤ 100000 , 1 ≤ a i ≤ 1 0 9 1 \leq n \leq 100000,1 \leq a_{i} \leq 10^{9} 1≤n≤100000,1≤ai≤109 。
试题 G: 交通信号
时间限制: 3.0 s 3.0 \mathrm{~s} 3.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 20 分
【问题描述】
LQ 市的交通系统可以看成由 n n n 个结点和 m m m 条有向边组成的有向图. 在每条边上有一个信号灯,会不断按绿黄红黄绿黄红黄… 的顺序循环 (初始时刚好变到绿灯)。当信号灯为绿灯时允许正向通行, 红灯时允许反向通行, 黄灯时不允许通行。每条边上的信号灯的三种颜色的持续时长都互相独立, 其中黄灯的持续时长等同于走完路径的耗时。当走到一条边上时, 需要观察边上的信号灯,如果允许通行则可以通过此边, 在通行过程中不再受信号灯的影响: 否则需要等待, 直到允许通行。
请问从结点 s s s 到结点 t t t 所需的最短时间是多少, 如果 s s s 无法到达 t t t 则输出 -1 。
【输入格式】
输入的第一行包含四个整数 n , m , s , t n, m, s, t n,m,s,t, 相邻两个整数之间用一个空格分哹。
接下来 m m m 行, 每行包含五个整数 u i , v i , g i , r i , d i u_{i}, v_{i}, g_{i}, r_{i}, d_{i} ui,vi,gi,ri,di, 相邻两个整数之间用一个空格分隔, 分别表示一条边的起点, 终点, 绿灯、红灯的持续时长和距离 (黄灯的持续时长)。
【输出格式】
输出一行包含一个整数表示从结点 s s s 到达 t t t 所需的最短时间。
【样例输入】
4 4 1 4 4414 4414
1 2 1 2 6 12126 12126
4 2 1 1 5 42115 42115
1 3 1 1 1 13111 13111
3 4 1 99 1 341991 341991
【样例输出】
11 11 11
【评测用例规模与约定】
对于 40 % 40 \% 40% 的评测用例, n ≤ 500 , 1 ≤ g i , r i , d i ≤ 100 n \leq 500,1 \leq g_{i}, r_{i}, d_{i} \leq 100 n≤500,1≤gi,ri,di≤100 ;
对于 70 % 70 \% 70% 的评测用例, n ≤ 5000 n \leq 5000 n≤5000 :
对于所有评测用例, 1 ≤ n ≤ 100000 , 1 ≤ m ≤ 200000 , 1 ≤ s , t ≤ n 1 \leq n \leq 100000,1 \leq m \leq 200000,1 \leq s, t \leq n 1≤n≤100000,1≤m≤200000,1≤s,t≤n, 1 ≤ u i , v i ≤ n , 1 ≤ g i , r i , d i ≤ 1 0 9 1 \leq u_{i}, v_{i} \leq n, 1 \leq g_{i}, r_{i}, d_{i} \leq 10^{9} 1≤ui,vi≤n,1≤gi,ri,di≤109 。
试题 H \mathrm{H} H : 点亮
时间限制: 3.0 s 3.0 \mathrm{~s} 3.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 20 分
【问题描述】
小蓝最近迷上了一款名为 《点亮》的迷题游戏, 游戏在一个 n × n n \times n n×n 的格子棋盘上进行, 棋盘由黑色和白色两种格子组成, 玩家在白色格子上放置灯泡, 确保任意两个灯泡不会相互照射, 直到整个棋盘上的白色格子都被点亮(每个谜题均为唯一解)。灯泡只会往水平和垂直方向发射光线, 照亮整行和整列, 除非它的光线被黑色格子挡住。黑色格子上可能有从 0 到 4 的整数数字, 表示与其上下左右四个相邻的白色格子共有几个奵泡; 也可能没有数字, 这表示可以在上下左右四个相邻的白色格子处任意选择几个位置放置灯泡。游戏的目标是选择合适的位置放置灯泡, 使得整个棋盘上的白色格子都被照亮。
例如, 有一个黑色格子处数字为 4 , 这表示它周围必须有 4 个灯泡, 需要在他的上、下、左、右处分别放置一个灯泡: 如果一个黑色格子处数字为 2 , 它的上下左右相邻格子只有 3 个格子是白色格子, 那么需要从这三个白色格子中选择两个来放置灯泡; 如果一个黑色格子没有标记数字, 且其上下左右相邻格子全是白色格子, 那么可以从这 4 个白色格子中任选出 0 至 4 个来放置灯泡。
题目保证给出的数据是合法的, 黑色格子周围一定有位置可以放下对应数量的奵泡。且保证所有谜题的解都是唯一的。
现在,给出一个初始的棋盘局面,请在上面放置好灯泡,使得整个棋盘上的白色格子被点亮。
【输入格式】
输入的第一行包含一个整数 n n n, 表示棋盘的大小。
接下来 n n n 行, 每行包含 n n n 个字符, 表示给定的棋盘。字符. 表示对应的格子为白色, 数字字符 0 、 1 、 2 、 3 、 4 0 、 1 、 2 、 3 、 4 0、1、2、3、4 表示一个有数字标识的黑色格子, 大写字母 X 表示没有数字标识的黑色格子。
【输出格式】
输出 n n n 行, 每行包含 n n n 个字符, 表示答案。大写字母 ○ 表示对应的格子包含奵泡, 其它字符的意义与输入相同。
【样例输入】

【样例输出】

【样例说明】
答案对应的棋盘布局如下图所示:
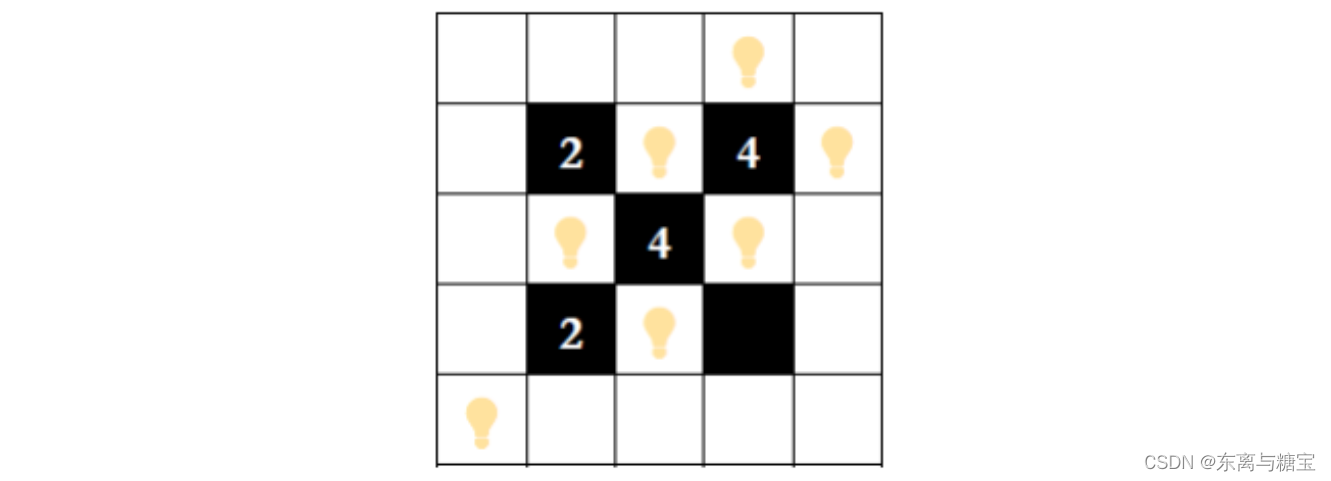
【评测用例规模与约定】
对于所有评测用例, 2 ≤ n ≤ 5 2 \leq n \leq 5 2≤n≤5, 且棋盘上至少有 15 % 15 \% 15% 的格子是黑色格子。
试题 I: 打折
时间限制: 5.0 s 5.0 \mathrm{~s} 5.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 25 分
【问题描述】
小蓝打算采购 n n n 种物品, 每种物品各需要 1 个。小蓝所住的位置附近一共有 m m m 个店铺, 每个店铺都出售着各种各样的物品。
第 i i i 家店铺会在第 s i s_{i} si 天至第 t i t_{i} ti 天打折, 折扣率为 p i p_{i} pi, 对于原件为 b b b 的物品, 折后价格为 ⌊ b ⋅ p j 100 ⌋ \left\lfloor\frac{b \cdot p j}{100}\right\rfloor ⌊100b⋅pj⌋ 。其它时间需按原价购买。
小蓝很仙, 他只能选择一天的时间去采购这些物品。请问, 他最少需要花多少钱才能买到需要的所有物品。
题目保证小蓝一定能买到需要的所有物品。
【输入格式】
输入的第一行包含两个整数 n , m n, m n,m, 用一个空格分隔, 分别表示物品的个数和店铺的个数。
接下来依次包含每个店铺的描述。每个店铺由若干行组成, 其中第一行包含四个整数 s i , t i , p i , c i s_{i}, t_{i}, p_{i}, c_{i} si,ti,pi,ci, 相邻两个整数之间用一个空格分隔, 分别表示商店优惠的起始和结束时间、折扣率以及商店内的商品总数。之后接 c i c_{i} ci 行, 每行包含两个整数 a j , b j a_{j}, b_{j} aj,bj, 用一个空格分隔, 分别表示该商店的第 j j j 个商品的类型和价格。商品的类型由 1 至 n n n 编号。
【输出格式】
输出一行包含一个整数表示小蓝需要花费的最少的钱数。
【样例输入】
2 2 22 22
1 2 89 1 12891 12891
9 7 97 97
3 4 77 1 34771 34771
2 15 215 215
【样例输出】
101 101 101
【评测用例规模与约定】
对于 40 % 40 \% 40% 的评测用例, n , m ≤ 500 , s i ≤ t i ≤ 100 , ∑ c i ≤ 2000 n, m \leq 500, s_{i} \leq t_{i} \leq 100, \sum c_{i} \leq 2000 n,m≤500,si≤ti≤100,∑ci≤2000;
对于 70 % 70 \% 70% 的评测用例, n , m ≤ 5000 , ∑ c i ≤ 20000 n, m \leq 5000, \sum c_{i} \leq 20000 n,m≤5000,∑ci≤20000;
对于所有评测用例, 1 ≤ n , m ≤ 100000 , 1 ≤ c i ≤ n , ∑ c i ≤ 400000 1 \leq n, m \leq 100000,1 \leq c_{i} \leq n, \sum c_{i} \leq 400000 1≤n,m≤100000,1≤ci≤n,∑ci≤400000, 1 ≤ s i ≤ t i ≤ 1 0 9 , 1 < p i < 100 , 1 ≤ a j ≤ n , 1 ≤ b j ≤ 1 0 9 1 \leq s_{i} \leq t_{i} \leq 10^{9}, 1<p_{i}<100,1 \leq a_{j} \leq n, 1 \leq b_{j} \leq 10^{9} 1≤si≤ti≤109,1<pi<100,1≤aj≤n,1≤bj≤109 。
试题 J: 宝石收集
时间限制: 5.0 s 5.0 \mathrm{~s} 5.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 25 分
【问题描述】
小蓝最近迷上了一欨收集宝石的游戏, 在游戏中给出了一幅藏宝图, 藏宝图可以看做是由 n n n 个顶点组成的一个有向图, 顶点编号为 0 , 1 , 2 , ⋯ , n − 1 0,1,2, \cdots, n-1 0,1,2,⋯,n−1 。每个顶点有且仅有一颗宝石,可能是红宝石或蓝宝石。
小蓝有一次收集宝石的机会, 他可以任意选择一个顶点当做起点, 沿着有向边前进, 经过的顶点上的宝石都会被自动收集 (包括起点和终点), 直到前方无路可走或者小蓝想退出时停止本次收集。小蓝可以多次经过同一个顶点, 但只会在第一次到达顶点时获得宝石, 后面再次到达时不会再获得宝石。
收集结束后, 小蓝可以用手中的宝石合成紫晶宝石: 一颗红宝石加一颗蓝宝石就可以合成一颗紫晶宝石。
小蓝想在收集结束后合成尽可能多的紫晶宝石, 请帮他规划出一条最优路径, 告诉他最多可以合成多少颗紫晶宝石。
【输入格式】
输入的第一行包含一个整数 n n n, 表示有顶点的个数。
第二行包含一个由 0 、 1 0 、 1 0、1 组成的长度为 n n n 的字符串, 从左至右依次表示第 0 至 n − 1 n-1 n−1 个顶点处宝石的种类, 0 表示红宝石, 1 表示蓝宝石。
第三行包含一个整数 m m m ,表示图中有 m m m 条有向边。
接下来 m m m 行, 每行包含两个整数 s , t s, t s,t, 用一个空格分隔, 表示一条从 s s s 到 t t t 的有向边。
【输出格式】
输出一行包含一个整数, 表示小蓝最多能合成几颗紫晶宝石。
【样例输入】
6 6 6
000111 000111 000111
6 6 6
0 1 01 01
1 2 12 12
3 1 31 31
2 3 23 23
2 4 24 24
2 5 25 25
【样例输出】
2 2 2
【样例说明】

样例如上图所示, 选择 0 号顶点作为起点, 按照 0 → 1 → 2 → 3 → 1 → 0 \rightarrow 1 \rightarrow 2 \rightarrow 3 \rightarrow 1 \rightarrow 0→1→2→3→1→ 2 → 4 2 \rightarrow 4 2→4 的行进路线, 可以获得 3 颗红宝石和 2 颗蓝宝石, 最终可以合成 2 颗紫晶宝石: 他也可以按照 1 → 2 → 3 → 1 → 2 → 4 1 \rightarrow 2 \rightarrow 3 \rightarrow 1 \rightarrow 2 \rightarrow 4 1→2→3→1→2→4 行进, 结果也是 2 。找不到比 2 更大的答案了。
【评测用例规模与约定】
对于所有的评测用例, 1 ≤ n ≤ 2000 , 0 ≤ m ≤ 1 0 5 , 0 ≤ s ≤ n − 1 1 \leq n \leq 2000,0 \leq m \leq 10^{5}, 0 \leq s \leq n-1 1≤n≤2000,0≤m≤105,0≤s≤n−1, 0 ≤ t ≤ n − 1 0 \leq t \leq n-1 0≤t≤n−1 。



