力扣72. 编辑距离（动态规划）_力扣编辑距离

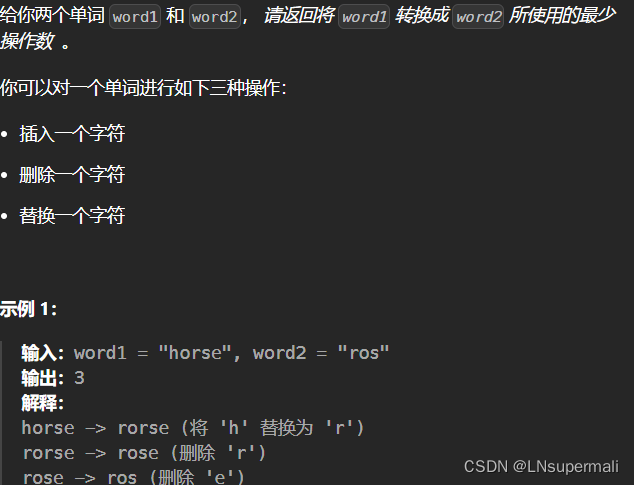
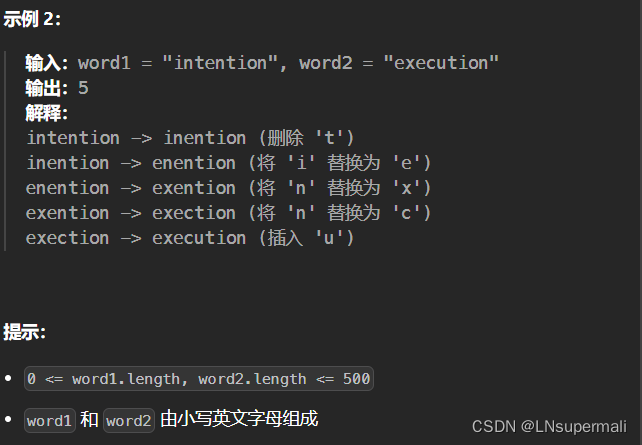
Problem: 72. 编辑距离

题目描述

思路

由于易得将字符串word1向word2转换和word2向word1转换是等效的，则我们假定统一为word1向word2转换！！！

1.确定状态：我们假设现在有下标i，j分别指向字符串word1和word2尾部的字符，dp(i,j)表示当前的操作则：

1.1. dp(i- 1, j) + 1;表示删除，直接把word1[i]的这个字符删除掉，并前移i，继续跟j对比，同时操作数加一；
1.2. dp(i, j - 1) + 1;表示插入，直接把word1[1]处的这个字符插入到word2[j]处，并前移动j，继续和i对比；同时操作数加一；
1.3. dp(i - 1, j - 1) + 1;表示替换，将word1[i]替换为word2[j],同时往前移动i，j继续对比，同时操作数加一

2.确定状态转移方程：由于上述易得dp[i][j] = min(dp[i - 1][j] + 1;dp[i][j - 1] + 1;dp[i - 1][j - 1] + 1);

复杂度

时间复杂度:

$O(m\times n)$

空间复杂度:

$O(m\times n)$

Code

class Solution {
public:
    /**
     * Dynamic programming
     *
     * @param word1 Given string1
     * @param word2 Given string2
     * @return int
     */
    int minDistance(string word1, string word2) {
        int word1Len = word1.length();
        int word2Len = word2.length();
        vector<vector<int>> dp(word1Len + 1, vector<int>(word2Len + 1));
        for (int i = 1; i <= word1Len; ++i) {
            dp[i][0] = i;
        }
        for (int j = 1; j <= word2Len; ++j) {
            dp[0][j] = j;
        }

        for (int i = 1; i <= word1Len; ++i) {
            for (int j = 1; j <= word2Len; ++j) {
                if (word1.at(i - 1) == word2.at(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    dp[i][j] = min3(dp[i - 1][j] + 1, dp[i][j - 1] + 1, dp[i - 1][j - 1] + 1);
                }
            }
        }
        return dp[word1Len][word2Len];
    }
    /**
     * Find the maximum of the three numbers
     *
     * @param a Given number
     * @param b Given number
     * @param c Given number
     * @return int
     */
    int min3(int a, int b, int c) {
        return min(a, min(b, c));
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43