秒懂百科，C++如此简单丨第十九天：动态规划

目录

动态规划的初步理解

求最短路径数

洛谷 P1002 过河卒 

题目描述

输入样例

输出样例 

思路

AC Code

---

Everyday English

The greatest glory in living lies not in never falling, but in rising every time we fall.
生命中最大的荣耀不在于从未跌倒，而在于每次跌倒后都能重新站起来。

动态规划的初步理解

什么是动态规划？最直白的理解就是动态的规划。

那高级一点的理解呢？就是每时每刻都拿着一个小本本，也就是记事本，把干的事情都记录下来，不断规划自己的策略，这就是动态规划。

动态规划里的小本本就对应着程序里的数组，而策略不就是往里依次填值吗。

动态规划理解到这，恭喜你，你已经了解了动态规划了。简单吧！

那我们边讲题，边理解！

动态规划我们一般用dp来表示。

求最短路径数

问从A（1,1）走到B（n,m）有几种最短路径（每次只能向相邻的格子走一格）？

要求：输入B的行坐标(n)和列坐标(m)，输出最短路径总数

这题咋一看，毫无头绪，是嵌套for循环？还是while？都不是，是DP，你看：

假设输入的是2和3，那么先把格子画出来，是这样的。

那每个格子里该填什么呢？对了，应该填到当前格子的最短路径数。那是不是每个格子都要从头输一遍呢？你仔细想想，题目说要最短，那走回头路肯定不行，那只能往下走或者右走，这样才能确保最短。因此每一格的最短路径数，不就是它上面的格子+左边的格子吗？

知道了DP公式，那好做了。

填完就是这样的，你可以验证一下：

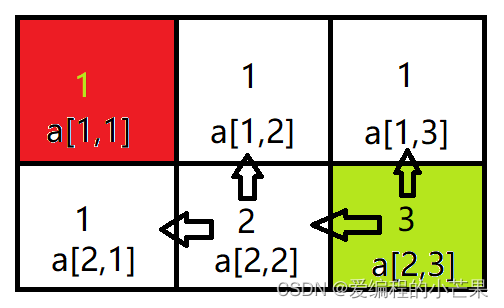
最后输出dp[n][m]就完事了，上代码：

#include<bits/stdc++.h>
using namespace std;
int main()
{
	int n,m,dp[505][505];
	memset(dp,0,sizeof(dp)); 
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			if(i==1&&j==1) dp[i][j]=1;//第一个格子只有一条路径 
			else
			{
				dp[i][j]=dp[i-1][j]+dp[i][j-1];
			}
		}
	}
	cout<<dp[n][m]<<endl;
	return 0; 
}

洛谷 P1002 过河卒 

网址：[NOIP2002 普及组] 过河卒 - 洛谷

题目描述

棋盘上 A 点有一个过河卒，需要走到目标 B 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 C 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，A 点 (0,0)、B 点 (n,m)，同样马的位置坐标是需要给出的。

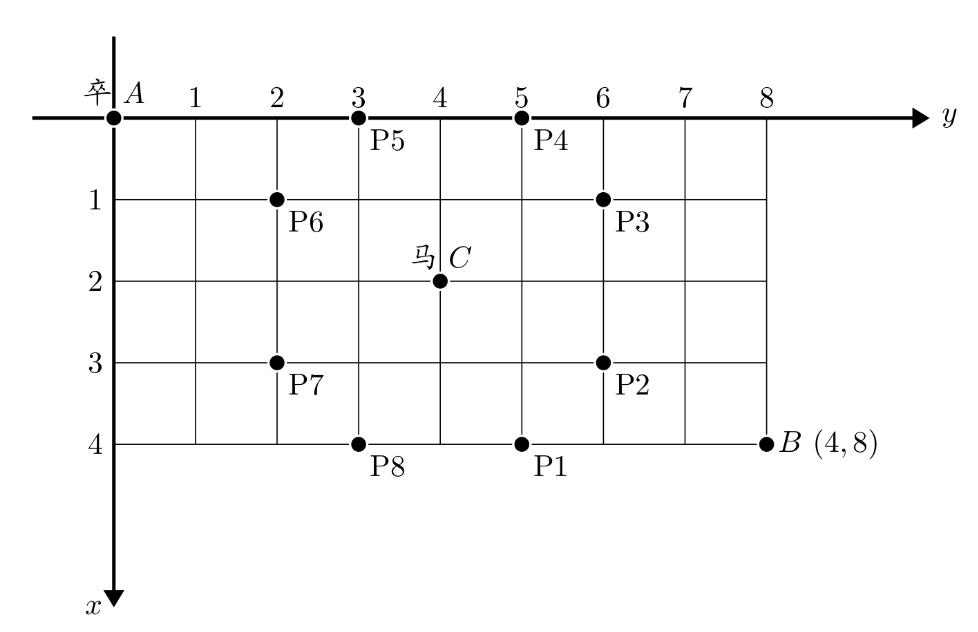
现在要求你计算出卒从 A 点能够到达 B 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入样例

6 6 3 3

输出样例 

6

思路

这题看上去不就是DFS吗，简简单单直接提交，可是…… 

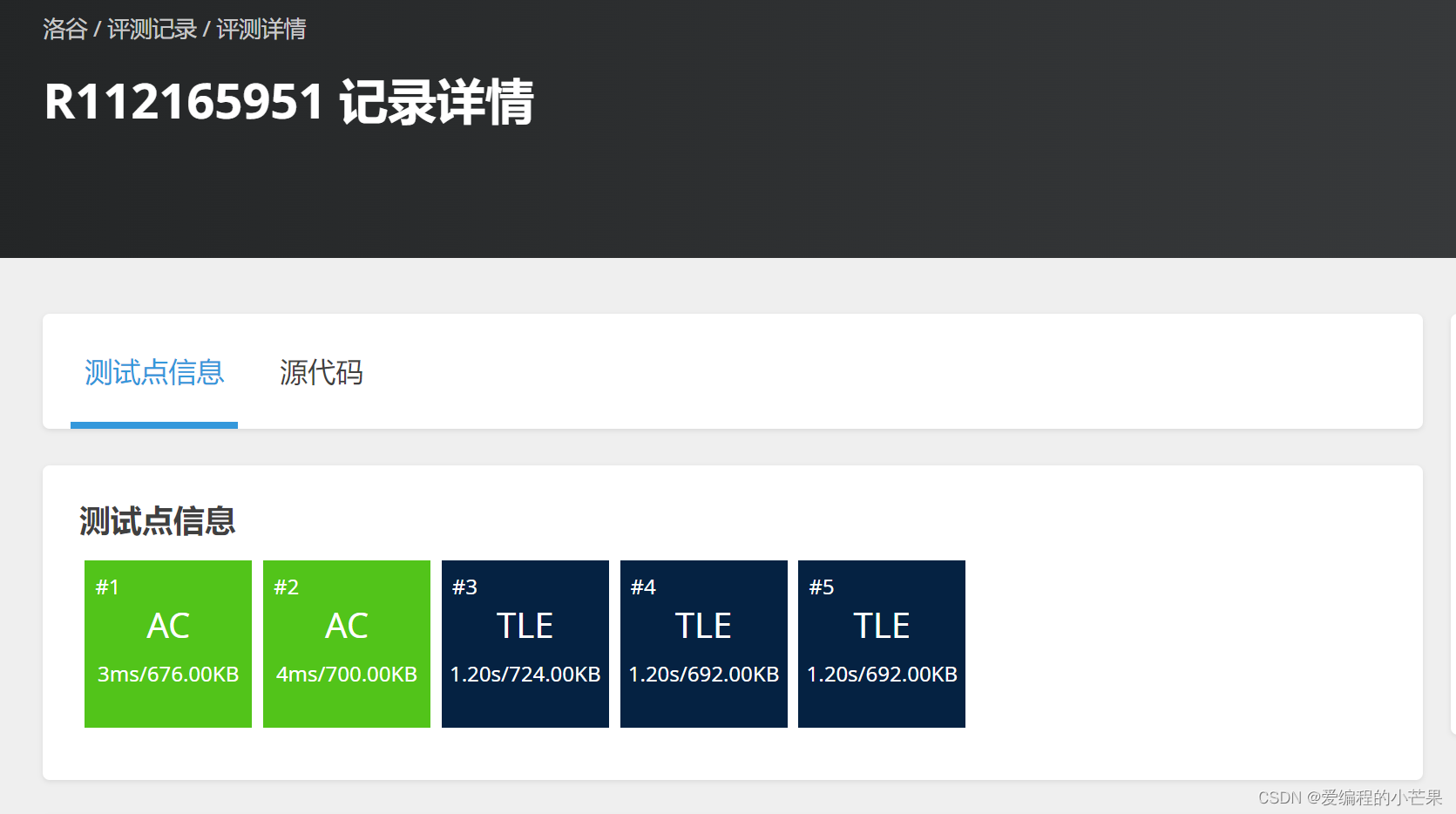
成功的超了时，那咋办，对了之前我不是讲过DP吗，没看的回我主页看看。这题数据较大，用DP不快吗？

那DP公式是啥呢？这里需要用到象棋知识，当卒过河后是不能向后走的，那么DP数组的每一格就是他上一格的路径数+左边一格的路径数（这个和我讲的DP特别像，不理解的去看我的DP文章）。当然马能拦住的地方开始都得给他设成不能走。

那代码不就So Easy了吗，上代码：

AC Code

#include<iostream>
#include<algorithm>
using namespace std;
long long dp[30][30];
int dx[8]={-2,-2,-1,-1,1,1,2,2},dy[8]={1,-1,2,-2,2,-2,1,-1};//马跳的坐标变化
 
int main(){
    int n,m,x,y;
    cin>>n>>m>>x>>y;
    n+=1;m+=1;x+=1;y+=1;
    for(int i=0;i<8;i++){
    	int nx=x+dx[i];
    	int ny=y+dy[i];
        if(nx>=1&&nx<=n&&ny>=1&&ny<=m)
            dp[nx][ny]=-1;
    }
    dp[1][0]=1;
    dp[x][y]=-1;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            if(dp[i][j]==-1)
                dp[i][j]=0;
            else{
                dp[i][j]=dp[i-1][j]+dp[i][j-1];
            }
        }
    }
 
    cout<<dp[n][m];
	return 0;
}