关于Transformer中常遇到的问题解答

来源：知乎

作者：红豆君  中国科学院大学 计算机硕士

文章经过作者同意转载

1. Transformer如何解决梯度消失问题的?

残差

   2. 为何Transformer中使用LN而不用BN?

BatchNorm是对一个batch-size样本内的每个特征做归一化，LayerNorm是对每个样本的所有特征做归一化。

形象点来说，假设有一个二维矩阵。行为batch-size，列为样本特征。那么BN就是竖着归一化，LN就是横着归一化。

它们的出发点都是让该层参数稳定下来，避免梯度消失或者梯度爆炸，方便后续的学习。但是也有侧重点。

一般来说，如果你的特征依赖于不同样本间的统计参数，那BN更有效。因为它抹杀了不同特征之间的大小关系，但是保留了不同样本间的大小关系。（CV领域）

而在NLP领域，LN就更加合适。因为它抹杀了不同样本间的大小关系，但是保留了一个样本内不同特征之间的大小关系。对于NLP或者序列任务来说，一条样本的不同特征，其实就是时序上字符取值的变化，样本内的特征关系是非常紧密的。

3. LN的作用是什么？

允许使用更大的学习率，加速训练。有一定的抗过拟合作用，使训练过程更加平稳

4. 多头自注意力层中的“多头”如何理解，有什么作用？

有点类似于CNN的多个卷积核。通过三个线性层的映射，不同头中的Q、K、V是不一样的，而这三个线性层的权重是先初始化后续通过学习得到的。不同的权重可以捕捉到序列中不同的相关性。

5. Transformer是自回归模型还是自编码模型？

自回归模型。

所谓自回归，即使用当前自己预测的字符再去预测接下来的信息。Transformer在预测阶段（机器翻译任务）会先预测第一个字，然后在第一个预测的字的基础上接下来再去预测后面的字，是典型的自回归模型。Bert中的Mask任务是典型的自编码模型，即根据上下文字符来预测当前信息。

6. 原论文中Q、K矩阵相乘为什么最后要除以√dk?

当 √dk 特别小的时候，其实除不除无所谓。无论编码器还是解码器Q、K矩阵其实本质是一个相同的矩阵。Q、K相乘其实相等于Q乘以Q的转置，这样造成结果会很大或者很小。小了还好说，大的话会使得后续做softmax继续被放大造成梯度消失，不利于梯度反向传播。

7. 原论中编码器与解码器的Embedding层的权重为什么要乘以√dmodel ?

为了让embedding层的权重值不至于过小，乘以 √dmodel  后与位置编码的值差不多，可以保护原有向量空间不被破坏。

8. Transformer在训练与验证的时候有什么不同

Transformer在训练的时候是并行的，在验证的时候是串行的。这个问题与Transformer是否是自回归模型考察的是同一个知识点。

9. Transformer模型的计算复杂度是多少？

n²d

n是序列长度，d是embedding的长度。Transformer中最大的计算量就是多头自注意力层，这里的计算量主要就是QK相乘再乘上V，即两次矩阵相乘。

QK相乘是矩阵【n d】乘以【d n】，这个复杂度就是n²d。

10. Transformer中三个多头自注意力层分别有什么意义与作用？

Transformer中有三个多头自注意力层，编码器中有一个，解码器中有两个。

编码器中的多头自注意力层的作用是将原始文本序列信息做整合，转换后的文本序列中每个字符都与整个文本序列的信息相关（这也是Transformer中最创新的思想，尽管根据最新的综述研究表明，Transformer的效果非常好其实多头自注意力层并不占据绝大贡献）。示意图如下：

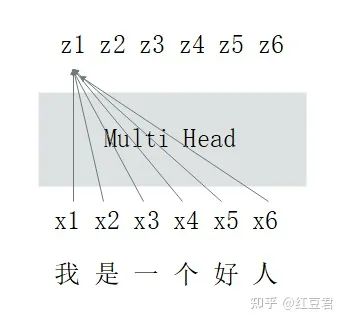
解码器的第一个多头自注意力层比较特殊，原论文给其起名叫Masked Multi-Head-Attention。其一方面也有上图介绍的作用，即对输入文本做整合（对与翻译任务来说，编码器的输入是翻译前的文本，解码器的输入是翻译后的文本）。另一个任务是做掩码，防止信息泄露。拓展解释一下就是在做信息整合的时候，第一个字符其实不应该看到后面的字符，第二个字符也只能看到第一个、第二个字符的信息，以此类推。

解码器的第二个多头自注意力层与编码器的第一个多头自注意力层功能是完全一样的。不过输入需要额外强调下，我们都知道多头自注意力层是通过计算QKV三个矩阵最后完成信息整合的。在这里，Q是解码器整合后的信息，KV两个矩阵是编码器整合后的信息，是两个完全相同的矩阵。QKV矩阵相乘后，翻译前与翻译后的文本也做了充分的交互整合。至此最终得到的向量矩阵用来做后续下游工作。

11. Transformer中的mask机制有什么作用

有两个作用。

1. 对不等长的序列做padding补齐

2. 掩码防止信息泄露

12. mask机制分别用在了哪里？

结合第十一问。

mask机制的作用1在三个多头自注意力层中都用了，作用2只用在了解码器的第一个多头自注意力层。

to be contiune

看大家点赞量啦！

推荐阅读

为何Transformer在计算机视觉中如此受欢迎？

如何看待swin transformer成为ICCV2021的 best paper？

熬了一晚上，我从零实现了Transformer模型，把代码讲给你听