很楠不爱3

这个屌丝很懒，什么也没留下！

热门标签

Graph Attention Network (GAT) 的Tensorflow版代码解析_in_drop != 0.0啥意思

作者：很楠不爱3 | 2024-04-06 00:52:20

踩

in_drop != 0.0啥意思

文章目录

关于GAT的基本原理解析可查看另一篇博客： Graph Attention Network (GAT) 图注意力模型
这里主要对其Tensorflow版本的代码进行解读，其中也会涉及GAT中的一些核心公式。
首先还是给出GAT的示意图：
在这里插入图片描述
GAT的Tensorflow版本实现代码Github地址：https://github.com/PetarV-/GAT

代码结构

.
├── data    		# Cora数据集
├── models    		# GAT模型定义 (gat.py)
├── pretrained   	# 预训练的模型
└── utils    		#  工具定义
1
2
3
4
5

参数设置

GAT/execute_cora.py

# training params
batch_size = 1
nb_epochs = 100000
patience = 100
lr = 0.005  # learning rate
l2_coef = 0.0005  # weight decay
hid_units = [8] # numbers of hidden units per each attention head in each layer
n_heads = [8, 1] # additional entry for the output layer
residual = False
nonlinearity = tf.nn.elu
model = GAT
1
2
3
4
5
6
7
8
9
10
11

数据加载

GAT源码默认使用的是cora数据集。cora的相关介绍可以参考：Cora数据集介绍
数据预处理部分和GCN源码相同：GCN代码分析
最终载入的数据adj为邻接矩阵，表示2708篇文章之间的索引关系。feature表示1433个单词在2708篇文章中是否存在。

GAT/utils/process.py

def load_data(dataset_str):
...
print(adj.shape)  # (2708, 2708)
print(features.shape)  #(2708, 1433)
1
2
3
4

特征预处理

GAT/utils/process.py

def preprocess_features(features):
    """Row-normalize feature matrix and convert to tuple representation"""
    rowsum = np.array(features.sum(1))
    r_inv = np.power(rowsum, -1).flatten()
    r_inv[np.isinf(r_inv)] = 0.
    r_mat_inv = sp.diags(r_inv)

    features = r_mat_inv.dot(features)
    return features.todense(), sparse_to_tuple(features)
1
2
3
4
5
6
7
8
9

模型定义

GAT核心定义：layers.py

def attn_head(seq, out_sz, bias_mat, activation, in_drop=0.0, coef_drop=0.0, residual=False):
    with tf.name_scope('my_attn'):
        if in_drop != 0.0:
            seq = tf.nn.dropout(seq, 1.0 - in_drop)

        seq_fts = tf.layers.conv1d(seq, out_sz, 1, use_bias=False) 

        # simplest self-attention possible
        f_1 = tf.layers.conv1d(seq_fts, 1, 1)
        f_2 = tf.layers.conv1d(seq_fts, 1, 1)
        logits = f_1 + tf.transpose(f_2, [0, 2, 1])
        coefs = tf.nn.softmax(tf.nn.leaky_relu(logits) + bias_mat)

        if coef_drop != 0.0:
            coefs = tf.nn.dropout(coefs, 1.0 - coef_drop)
        if in_drop != 0.0:
            seq_fts = tf.nn.dropout(seq_fts, 1.0 - in_drop)

        vals = tf.matmul(coefs, seq_fts)
        ret = tf.contrib.layers.bias_add(vals)

        # residual connection
        if residual:
            if seq.shape[-1] != ret.shape[-1]:
                ret = ret + conv1d(seq, ret.shape[-1], 1) # activation
            else:
                ret = ret + seq

        return activation(ret)  # activation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

这里有 3 个比较核心的参数：

seq 指的是输入的节点特征矩阵，大小为 [num_graph, num_node, fea_size]
out_sz 指的是变换后的节点特征维度，也就是 $Wh_i$ 后的节点表示维度。
bias_mat 是经过变换后的邻接矩阵，大小为 [num_node, num_node]。

下面来看几行重点代码的解读：

seq_fts = tf.layers.conv1d(seq, out_sz, 1, use_bias=False) # [num_graph, num_node, out_sz]
1

作者首先对原始节点特征 seq 利用卷积核大小为 1 的 1D 卷积模拟投影变换得到了 seq_fts，投影变换后的维度为 out_sz。注意，这里投影矩阵 $W$ 是所有节点共享，所以 1D 卷积中的多个卷积核也是共享的。
输出seq_fts 对应于公式中的 $Wh$ ，shape为 [num_graph, num_node, out_sz]。

f_1 = tf.layers.conv1d(seq_fts, 1, 1) # [num_graph, num_node, 1]
f_2 = tf.layers.conv1d(seq_fts, 1, 1) # [num_graph, num_node, 1]
1
2

投影变换后得到的seq_fts继续使用卷积核大小为 1 的 1D 卷积处理，得到节点本身的投影f_1 和其邻居的投影f_2，对应于论文公式中的 $a(Wh_i, Wh_j)$ 。注意这里两个投影的参数是分开的，即有两套投影参数 $a_1$ 和 $a_2$ ，分别对应上面两个conv1d 中的参数。
经过 tf.layers.conv1d(seq_fts, 1, 1) 之后的 f_1 和 f_2 对应于公式中的 $a_1Wh_i$ 和 $a_2Wh_j$ ，维度均为 [num_graph, num_node, 1]。

logits = f_1 + tf.transpose(f_2, [0, 2, 1]) # [num_graph, num_node, num_node] 
1

将 f_2 转置之后与 f_1 叠加，通过Tensorflow的广播机制得到的大小为 [num_graph, num_node, num_node] 的 logits，就是一个注意力矩阵：
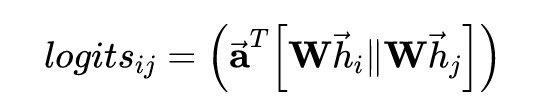
在这里插入图片描述

coefs = tf.nn.softmax(tf.nn.leaky_relu(logits) + bias_mat)
1

接下来, 按照 GAT 的公式，我们只要对 logits 进行 softmax 归一化就可以得到注意力权重，也就是代码里的 coefs。
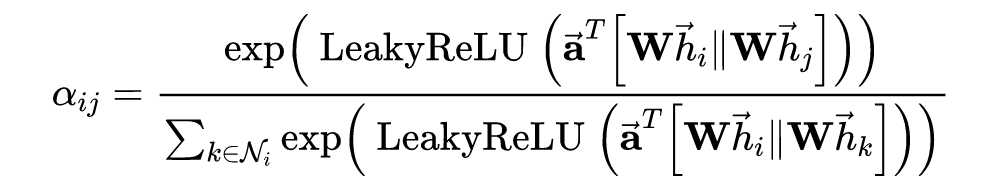在这里插入图片描述 但是，这里为什么会多一项 bias_mat 呢？

因为的 logits 存储了任意两个节点之间的注意力值，但是，归一化只需要对每个节点的所有邻居的注意力进行（ $k属于N_i$ ）。所以，引入了 bias_mat 就是将 softmax 的归一化对象约束在每个节点的邻居上，如下式的红色部分。
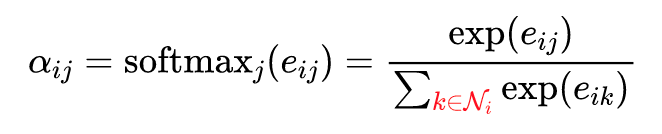
在这里插入图片描述
那么，bias_mat 是如何实现的呢？

直接的想法就是只含有 0,1 的邻接矩阵与注意力矩阵相乘，从而对邻居进行 mask。但是，直接用 0,1进行mask，由于softmax中有exp指数操作所以会有问题。

假设注意力权值 [1.2, 0.3, 2.4] 经过 [0,1,1] 的乘法 mask 得到 [0, 0.3, 2.4]，再送入到 softmax 归一化，实际上变为 $e^0, e^{0.3}, e^{0.4}]$ ，这里本应该被 mask 掉的 1.2 变成了 $e^0]$ =1，还是参与到了归一化的过程中。

作者这里用一个很大的负数，如 $- 1 e 9$ ，将原始邻居矩阵进行下面的变换。
utils/process.py/adj_to_bias

def adj_to_bias(adj, sizes, nhood=1):
    nb_graphs = adj.shape[0] # nb_graphs: 1
    # print('adj_to_bias.adj:', adj.shape) # adj: (1, 2708, 2708)
    # print('sizes:', sizes) # sizes = nb_nodes : 2708

    mt = np.empty(adj.shape) # np.empty返回维度为(1, 2708, 2708)的随机数组
    for g in range(nb_graphs): # nb_graphs: 1，此处 g=0 符合循环条件
        mt[g] = np.eye(adj.shape[1]) # mt[0]: (2708,2708) 对角线为1的矩阵
        for _ in range(nhood): # nhood: 1，此处循环变量=0符合循环条件
            mt[g] = np.matmul(mt[g], (adj[g] + np.eye(adj.shape[1]))) # 由于mt[g]为对角阵，故结果仍为(adj[g] + np.eye(adj.shape[1]))
            # print(adj[g] + np.eye(adj.shape[1]))  # adj(2708,2708) + eye(2708,2708)， 实现self-connection自环
        
        for i in range(sizes[g]):  # sizes[g]: 2708
            for j in range(sizes[g]):
                if mt[g][i][j] > 0.0: 
                    mt[g][i][j] = 1.0 # 将大于的0的元素设置为1.0
    return -1e9 * (1.0 - mt) # mt中值为1的位置返回0，值为0的位置返回负数-1e9
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

然后，将 bias_mat 和注意力矩阵相加，即 (tf.nn.leaky_relu(logits) + bias_mat)，进而将非节点邻居进行 mask。
例如，[1.2, 0.3, 2.4] 经过 $[- 1 e 9, 0, 0]$ 的加法 mask 得到 $e^{1.2-1e9}, e^{0.3}, e^{2.4}]=[0, e^{0.3}, e^{2.4}]$ 。这样 softmax 就达到了我们的目的。

vals = tf.matmul(coefs, seq_fts)
1

最后，将 mask 之后的注意力矩阵 coefs 与变换后的特征矩阵 seq_fts 相乘，即可得到更新后的节点表示 vals。对应于公式：
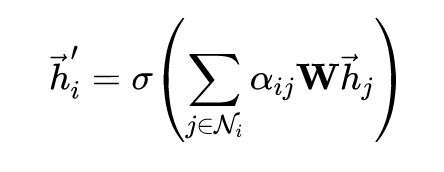
在这里插入图片描述

gat.py

logits = model.inference(ftr_in, nb_classes, nb_nodes, is_train,
                                attn_drop, ffd_drop,
                                bias_mat=bias_in,
                                hid_units=hid_units, n_heads=n_heads,
                                residual=residual, activation=nonlinearity)
1
2
3
4
5

class GAT(BaseGAttN):
    def inference(inputs, nb_classes, nb_nodes, training, attn_drop, ffd_drop,
            bias_mat, hid_units, n_heads, activation=tf.nn.elu, residual=False):
        attns = []
        
        #GAT中预设了8层attention head
        for _ in range(n_heads[0]): 
            attns.append(layers.attn_head(inputs, bias_mat=bias_mat,
                out_sz=hid_units[0], activation=activation,
                in_drop=ffd_drop, coef_drop=attn_drop, residual=False))
        h_1 = tf.concat(attns, axis=-1)

		#hid_units表示每一层attention head中的隐藏单元个数
        for i in range(1, len(hid_units)):
            h_old = h_1
            attns = []
            for _ in range(n_heads[i]):
                attns.append(layers.attn_head(h_1, bias_mat=bias_mat,
                    out_sz=hid_units[i], activation=activation,
                    in_drop=ffd_drop, coef_drop=attn_drop, residual=residual))
            h_1 = tf.concat(attns, axis=-1)
        out = []

		#加上输出层
        for i in range(n_heads[-1]):
            out.append(layers.attn_head(h_1, bias_mat=bias_mat,
                out_sz=nb_classes, activation=lambda x: x,
                in_drop=ffd_drop, coef_drop=attn_drop, residual=False))
        logits = tf.add_n(out) / n_heads[-1]
    
        return logits
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

base_gattn.py

GAT/models/base_gattn.py

定义损失函数。

    def loss(logits, labels, nb_classes, class_weights):
        sample_wts = tf.reduce_sum(tf.multiply(tf.one_hot(labels, nb_classes), class_weights), axis=-1)

		#交叉熵损失函数
        xentropy = tf.multiply(tf.nn.sparse_softmax_cross_entropy_with_logits(
                labels=labels, logits=logits), sample_wts)
        return tf.reduce_mean(xentropy, name='xentropy_mean')
1
2
3
4
5
6
7

定义训练函数。training最小化损失函数和L2 loss。

    def training(loss, lr, l2_coef):
        # weight decay
        vars = tf.trainable_variables()
        lossL2 = tf.add_n([tf.nn.l2_loss(v) for v in vars if v.name not
                           in ['bias', 'gamma', 'b', 'g', 'beta']]) * l2_coef
        # optimizer
        opt = tf.train.AdamOptimizer(learning_rate=lr)

        # training op
        train_op = opt.minimize(loss+lossL2)
        
        return train_op
1
2
3
4
5
6
7
8
9
10
11
12

参考资料：

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/很楠不爱3/article/detail/368856