二叉树深度优先遍历解题思路_深度优先遍历二叉树

1.二叉树深度优先遍历解题思路

1.1.三种深度优先遍历的方式

• 理解深度优先遍历的前提：
  
  任何一颗非空的二叉树，都有根结点，左子树和右子树。例如上面这颗二叉树，根结点是A，左子树的结点有B、C、D，右子树的结点有E、F。而任意一颗非空的二叉树的左子树和右子树也是一颗二叉树。
  
  上面这颗二叉树的根为B，左子树有C结点，右子树有D结点。 以B为根结点的左子树还是一颗二叉树。
  
  上面这颗二叉树的根结点是C，左子树和右子树是null。

---

• 先序遍历（先根遍历）
  先序遍历指的是，对于任意一颗二叉树，都先遍历其根结点，然后遍历其左子树，最后遍历其右子树。
  
  例如上面这颗二叉树，先序遍历的结果就是A-B-C-D-E-F;

//先序遍历
    public void preOrderTraversal(TreeNode root) {
        if (root == null) return;
        //对当前结点的实际工作 也可替换为其他语句
        System.out.print(root.val + " ");
        //实际工作结束
        this.preOrderTraversal(root.left);
        this.preOrderTraversal(root.right);
    }
1
2
3
4
5
6
7
8
9

---

• 中序遍历（中根遍历）
  中序遍历指的是，对于任意一颗二叉树，都先遍历其左子树，然后遍历其根节点，最后遍历其右子树。
  
  例如上面这颗二叉树，中序遍历的结果就是C-B-D-A-E-F;

//中序遍历
    public void inOrderTraversal(TreeNode root) {
        if (root == null) return;
        this.inOrderTraversal(root.left);
        //对当前结点的实际工作 也可替换为其他语句
        System.out.print(root.val + " ");
        //实际工作结束
        this.inOrderTraversal(root.right);
    }
1
2
3
4
5
6
7
8
9

---

• 后序遍历（后根遍历）
  后序遍历指的是，对于任意一颗二叉树，都先遍历其左子树，然后遍历其右子树，最后遍历其根结点。
  

  例如上面这颗二叉树，后序遍历的结果就是C-D-B-F-E-A;

//后序遍历
    public void postOrderTraversal(TreeNode root) {
        if (root == null) return;
        this.postOrderTraversal(root.left);
        this.postOrderTraversal(root.right);
        //对当前结点的实际工作 也可替换为其他语句
        System.out.print(root.val + " ");
        //实际工作结束
    }
1
2
3
4
5
6
7
8
9

1.2.深度优先遍历的启示

名词说明：由于本人表达能力有限，下面所提到的一些名词可能会让读者引起混淆。若在后面的文章阅读过程中对某些名词的含义产生了疑惑，可以翻到这里看一下对下面的出现的一些名词的说明。

1. 结点实际操作：指本次递归中对当前的结点（或含参）进行实际操作。
2. 结点实际操作顺序：对某个数据结构的结点实际操作的顺序。
3. 结点遍历顺序：结点实际操作顺序。
4. 结点调用顺序：指对某个数据结构中结点的实际访问顺序，或者说递归时的函数栈帧的开辟顺序。

1.2.1.递归形成条件

我们都理解，深度优先遍历的所使用的编码技巧是递归，而递归有形成的条件有3个：

1. 函数调用自身
2. 有一个终止条件
3. 不断朝终止条件步进

所谓的递归，就是函数不断调用自身的过程，在这个过程中，必须由一个终止递归的条件，否则函数就会不断地调用自身引发程序错误。那么问题就来了，既然是函数自己调用自己，所调用的函数名都是相同的，那么系统是怎么得知某次函数调用是最后一次，某次函数调用不是呢。答案是参数，不同的函数调用最大的区别就是函数参数。 一旦某次递归调用的函数的参数达成了某个条件，系统就得知：“好了，我的函数参数已经达到了终止条件了，我不该再递归下去了”。

---

我们都清楚了递归的本质是对参数进行操作，一切都要围绕参数进行。那么在单次的函数递归中，想清楚自己究竟要做什么，应该考虑的点有哪些呢？

1. 下一次递归的参数是什么？
2. 我该返回什么？（为了返回我想要的，我要怎么利用下一次递归的返回值？）
3. 我要对参数做什么？

也就是单次递归，只要搞清楚递什么（类似一个回旋镖，递什么参数，它返回什么），归（自己返回什么）什么就行了。

1.2.2递归过程的实际工作顺序

我们已经知道单次递归要做什么了，但整个递归的过程的考虑不应该只有这些，还有一个很重要的问题。在一次递归调用中，我既要把参数传给下一次递归并获得下一次递归的返回值（也可能没返回值），又要对参数操作，那操作当前参数和进行下一次递归，谁先谁后呢？

1.2.2.1.单路递归的实际工作顺序

所谓的单路递归，即在某次递归调用中，最多递归调用自己一次。典型的有对单链表进行递归，下次进行递归的参数就是自己的后继结点。

就单路递归，某一次函数调用，根据下一次函数调用和本次函数调用的工作的先后顺序，可以分为：

1. 我先把参数B（当前结点的后继）递给下一次递归， 等下一次递归返回的时候，我再操作参数A（当前结点），然后我再返回。
2. 我先操作参数A（当前结点），然后把参数B（当前结点的后继）递给下一次递归，等这个递归返回后，我再接受它的返回值，最后再返回我想要返回的值。

---

发现没有，就单路递归而言，操作参数和把递给下一次递归的先后顺序不同，你对单链表的实际操作顺序就不同了。第一种递归你从后往前操作单链表，第二个递归则是从前往后操作单链表。 换句话来说，第一种是逆向遍历单链表，第二种是正向遍历单链表。

当然还有不同的先后顺序安排，这里不再列举，只是想通过这个例子让你知道在单路递归中，函数调用中的下一次递归的和操作当前参数的执行先后顺序不同，实际的操作顺序截然不同。

这里也就得出了一个重要结论，遍历指的就是实际的业务操作顺序，而不是调用顺序。

1.2.2.2. 双路递归的实际工作顺序

双路递归顾名思义，每次函数调用都会递归调用两次，典型的有对二叉树进行深度优先遍历，对某个结点递归后，该节点的左右孩子也会参与递归。想一下对二叉树双路递归的不同的业务操作时机对实际二叉树结点的操作顺序的影响，你可能就已经开始头疼了。

列举三个在递归二叉树时，操作当前结点和进行下一次递归的不同先后顺序组合：

1在单次递归调用中，我先操作参数（当前根结点），然后递归调用左孩子结点，再递归调用右孩子结点，最后返回。
2在单次递归调用中，我先递归调用左孩子结点，然后操作参数（当前根结点），再递归调用右孩子结点。
1在单次递归调用中，我先递归调用左孩子结点，然后递归调用右孩子结点，再操作当前参数（当前根结点）。

问：这三种情况，二叉树结点的实际操作顺序是什么样的？

实际上，这三种递归方式说的的就是先序遍历，中序遍历和后序遍历，可以多多体会一下。

1.2.3.三种深度优先遍历给我们的启示是什么？

实际上，三种优先遍历告诉了我们递归过程中对二叉树结点的实际操作顺序，所谓的不同深度优先遍历方式等价于不同的二叉树结点实际操作顺序。 你会发现，三种深度优先遍历方式对二叉树结点的函数调用顺序都是相同的，但实际操作结点的顺序却是不同的。

例如后序遍历，从函数调用来看，你的函数调用的结点也是A-B-C，但实际操作的第一个结点却是C，演示如下：

1. 你在调用了A这个结点后，还没来得及操作，就马上递归调用B结点。

2. 同理B结点调用之后，你也还没操作，你就递归调用了C结点。

3. 还没来得及操作C，你又递归调用了C的左子树（空节点），检测到 参数不合法，递归返回到C结点中。

4. C左子树递归调用返回之后，才对C结点进行了实际的操作。

---

• 不管是哪一种深度优先遍历方式（先序，中序和后序），结点调用的顺序都是相同的，对结点的实际操作顺序却是不同的。

1.3.深度优先遍历二叉树解题模板

根据1.2的推论，我们可以对二叉树深度优先遍历的题目的解法得出一个结论：只要知道某道题的合适的深度优先遍历方式（实际工作顺序），递归的参数，返回的参数，就可以解答了。

1. 确定某道二叉树题目适合深度优先遍历，且知道最佳的深度遍历方式。
2. 根据深度遍历方式设计单次递归模板
   先序遍历：操作当前结点-左路递归-右路递归-返回
   中序遍历：左路递归-操作当前结点-右路递归-返回
   后序遍历：左路递归-右路递归-操作当前结点-返回
3. 确定左路递归和右路递归的参数和返回值
4. 编码

当然，并非所有的二叉树深度遍历题都适用这个模板，因为除了这三种还有其他的深度优先遍历方式，例如你可以——操作当前结点-右路递归-左路递归-返回。但在理解了最常见的三种深度遍历方式，其他的深度遍历方式可以类推了。

1.4.二叉树深度优先遍历题目的一些补充

对于一些特殊的深度优先遍历的题目，特别是一次递归的实际工作中需要操作一个以上二叉树结点的，由于一般来说一次函数调用我们只有一个结点的参数，不太好定位到其他的结点，所以我们可以考虑使用成员变量作为我们的辅助变量。

---

例题：

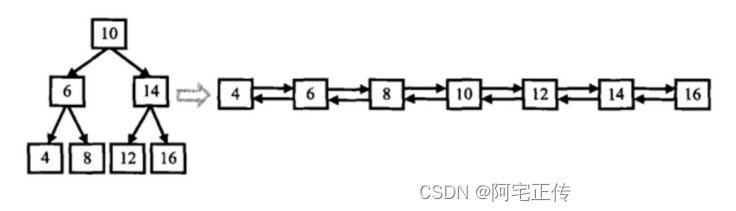
描述
输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。如下图所示

数据范围：输入二叉树的节点数 0≤n≤10000 \le n \le 10000≤n≤1000，二叉树中每个节点的值 0≤val≤10000\le val \le 10000≤val≤1000
要求：空间复杂度O(1)O(1)O(1)（即在原树上操作），时间复杂度 O(n)O(n)O(n)

注意:
1.要求不能创建任何新的结点，只能调整树中结点指针的指向。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继
2.返回链表中的第一个节点的指针
3.函数返回的TreeNode，有左右指针，其实可以看成一个双向链表的数据结构
4.你不用输出双向链表，程序会根据你的返回值自动打印输出
输入描述：
二叉树的根节点
返回值描述：
双向链表的其中一个头节点。
示例1
输入：

{10,6,14,4,8,12,16}

返回值：

From left to right are:4,6,8,10,12,14,16;From right to left are:16,14,12,10,8,6,4;

说明：

输入题面图中二叉树，输出的时候将双向链表的头节点返回即可。

示例2
输入：

{5,4,#,3,#,2,#,1}

返回值：

From left to right are:1,2,3,4,5;From right to left are:5,4,3,2,1;

说明：

                5
              /
            4
          /
        3
      /
    2
  /
1
1
2
3
4
5
6
7
8
9

树的形状如上图

题解

/**
public class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;

    public TreeNode(int val) {
        this.val = val;

    }

}
*/
//中序遍历二叉树 并改变当前二叉树的结点的左子树指向和前一个操作的二叉树的右子树指向（用成员变量存储）
public class Solution {
	//用成员变量记录上一次遍历的结点
    public TreeNode prev;
    public void inOrder(TreeNode root) {
        //递归结束条件判定
        if (root == null) return;
        //先递归左子树
        inOrder(root.left);
        //具体的工作
        root.left = prev;
        if (prev != null) prev.right = root;
        prev = root;
        //工作结束
        //递归右子树
        inOrder(root.right);
    }
    public TreeNode Convert(TreeNode root) {
        if (root == null) return null;
        inOrder(root);
        while (root.left != null) root = root.left;
        return root;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37