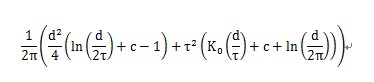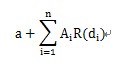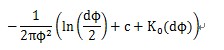薄板样条插值(Thin-plate Spline)
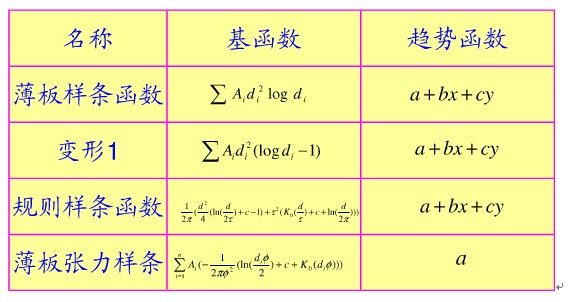
薄板样条函数建立一个通过控制点的面，并使所有点的坡度变化最小。换句话，薄板样条函数以最小曲率面拟合控制点。薄板样条函数的估计值由下式计算：
式中，x和y为要被插值得点的x、y坐标:di^2为（x,y）和（xi，yi）距离平方，xi、yi分别为控制点i的x、y坐标。
薄板样条函数包括两个部分：(a+bx+cy)表示局部趋势函数，它与线性或一阶趋势面具有相同的形式，前一部分 表示基本函数，可获得最小曲率的面。相关系数Ai，a、b、c由以下线性方程组决定：
式中，n为控制点的数目;fi为控制点i的已知值；系数的计算要求n+3个联立方程。
规则样条插值(Regularized Spline)
规则样条函数的近似值与薄板样条函数有相同的局部趋势函数，但是基本函数取不同形式：
式中,τ为权重；d为待定值的点和控制点i之间的距离，c为常数0.577215；K0（d/τ）为修正的零次贝塞尔函数。它可由一个多项式方程估计。Γ通常被设为[0，0.5]之间，因为更大的值会导致数据少的区域趋于过伸。
薄板张力样条插值
薄板张力样条法有如下表达式：
式中，a为趋势函数。基本函数R(d)为
式中， φ为权重。如果φ权重被设为接近于0，则张力法与基本薄板样条插值法得到的估计差相似。较大的φ值降低了薄板的刚度，结果插值的值域使得插值成的面与通过控制点的模形态相似。
薄板样条插值函数及其变异函数一般应用在平滑和连续的面，如高程或水平面。样条法也被用于对气候数据（如平均降水量）的插值。
样条插值求解步骤：
