热门标签
热门文章
- 1ImageNet图像数据集介绍_imagenet数据集包含了多少幅图片
- 2HCIA-HarmonyOS Application Developer——题目集2_hcip harmonyos application developer
- 3C# 百度编辑器显示异常 报错:Uncaught ReferenceError: UE is not defined
- 4CrossOver 23.6 for Mac/Linux 2024最新功能介绍及是如何进行下载、安装与激活的_crossover23linux如何使用
- 5使用OpenHarmonyNDK移植三方库Speexdsp_openharmony 编译 第三方库
- 6车牌检测License Plate Detection and Recognition in Unconstrained Scenarios_aolp数据集
- 7Qt/C++开发经验小技巧合集_mac qt c++开发指南
- 8计算机组成原理-练手题集合【期末复习|考研复习】
- 9零基础入门微信小程序开发
- 10【MySQL】-知识点整理
当前位置: article > 正文
MATLAB机器人工具箱【1】——建模+正逆运动学+雅克比矩阵_matlab六轴机械臂运动学建模和雅可比矩阵
作者:我家小花儿 | 2024-03-18 11:30:36
赞
踩
matlab六轴机械臂运动学建模和雅可比矩阵
本文在参考B站up主刘海涛大佬的视频分享基础上,结合自己学习的机器人学知识,利用MATLAB机器人工具箱加深理解和运用,机器人工具箱安装教程见Robotic toolbox 工具箱的安装和初步了解,安装了工具箱后就可以用来愉快的学习啦。
1. 二维空间位姿描述

2. 三维空间位姿描述

3. 建立机器人模型
根据自己的机器人模型实际参数采用标准DH法或者改进DH法建模,得到DH参数表,然后利用工具箱建模,下面是建模时必须要用到的两个类函数。
3.1 Link 类

3.2 SerialLink 类

3.3 建立机器人模型(展示)
关于puma560的DH参数表有很多版本,可以参考PUMA560机器人D-H参数和改进DH参数
这里以这一版本为例【和《机器人学》——蔡自兴版本保持一致】:

%%改进D-H模型 % 关节角 连杆偏距 连杆长度 连杆转角 % theta(i) d(i) a(i-1) alpha(i-1) offset SL1=Link([0 0 0 0 0 ],'modified'); SL2=Link([0 0.14909 0 -pi/2 0 ],'modified'); SL3=Link([0 0 0.4318 0 0 ],'modified'); SL4=Link([0 0.43307 0.02032 -pi/2 0 ],'modified'); SL5=Link([0 0 0 pi/2 0 ],'modified'); SL6=Link([0 0 0 -pi/2 0 ],'modified'); p560=SerialLink([SL1 SL2 SL3 SL4 SL5 SL6],'name','puma560');%SerialLink 类函数 %通过手动输入各个连杆转角,模型会自动运动到相应位置 %方法一: % p560.teach([-pi/2 -pi/2 0 0 0 0]); %方法二: p560.plot([-pi/2 -pi/2 0 0 0 0]);
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16

在MATLAB的机器人工具箱中提供了puma560机械臂模型,运行 mdl_puma560 命令,会发现自动生成四个1*6的关节角矩阵,他们分别代表以下状态:

4. 正逆运动学+雅克比矩阵


4.1 求解正运动学方程

【小技巧:相邻连杆变换矩阵第一列第三个元素如果是零的话,说明选择的是标准DH建模法,否则(就像上图所示)是改进DH法】
自己编写的正运动学函数:
function T06 = puma560_fk(theta1,theta2,theta3,theta4,theta5,theta6) a2 = 0.4318; a3 = 0.02032; d2 = 0.14909; d4 = 0.43307; T01 = [cos(theta1) -sin(theta1) 0 0; sin(theta1) cos(theta1) 0 0; 0 0 1 0; 0 0 0 1]; T12 = [cos(theta2) -sin(theta2) 0 0; 0 0 1 d2; -sin(theta2) -cos(theta2) 0 0; 0 0 0 1]; T23 = [cos(theta3) -sin(theta3) 0 a2; sin(theta3) cos(theta3) 0 0; 0 0 1 0; 0 0 0 1]; T34 = [cos(theta4) -sin(theta4) 0 a3; 0 0 1 d4; -sin(theta4) -cos(theta4) 0 0; 0 0 0 1]; T45 = [cos(theta5) -sin(theta5) 0 0; 0 0 -1 0; sin(theta5) cos(theta5) 0 0; 0 0 0 1]; T56 = [cos(theta6) -sin(theta6) 0 0; 0 0 -1 0; -sin(theta6) -cos(theta6) 0 0; 0 0 0 1]; T06 = T01*T12*T23*T34*T45*T56; end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
求解自己的正运动学公式:
%求正运动学公式
T06 = puma560_fk(theta1,theta2,theta3,theta4,theta5,theta6)
- 1
- 2
结果:
T06 =
[ sin(theta6)*(cos(theta4)*sin(theta1) + sin(theta4)*(cos(theta1)*sin(theta2)*sin(theta3) - cos(theta1)*cos(theta2)*cos(theta3))) + cos(theta6)*(cos(theta5)*(sin(theta1)*sin(theta4) - cos(theta4)*(cos(theta1)*sin(theta2)*sin(theta3) - cos(theta1)*cos(theta2)*cos(theta3))) - sin(theta5)*(cos(theta1)*cos(theta2)*sin(theta3) + cos(theta1)*cos(theta3)*sin(theta2))), cos(theta6)*(cos(theta4)*sin(theta1) + sin(theta4)*(cos(theta1)*sin(theta2)*sin(theta3) - cos(theta1)*cos(theta2)*cos(theta3))) - sin(theta6)*(cos(theta5)*(sin(theta1)*sin(theta4) - cos(theta4)*(cos(theta1)*sin(theta2)*sin(theta3) - cos(theta1)*cos(theta2)*cos(theta3))) - sin(theta5)*(cos(theta1)*cos(theta2)*sin(theta3) + cos(theta1)*cos(theta3)*sin(theta2))), sin(theta5)*(sin(theta1)*sin(theta4) - cos(theta4)*(cos(theta1)*sin(theta2)*sin(theta3) - cos(theta1)*cos(theta2)*cos(theta3))) + cos(theta5)*(cos(theta1)*cos(theta2)*sin(theta3) + cos(theta1)*cos(theta3)*sin(theta2)), (2159*cos(theta1)*cos(theta2))/5000 - (14909*sin(theta1))/100000 - (127*cos(theta1)*sin(theta2)*sin(theta3))/6250 + (127*cos(theta1)*cos(theta2)*cos(theta3))/6250 - (43307*cos(theta1)*cos(theta2)*sin(theta3))/100000 - (43307*cos(theta1)*cos(theta3)*sin(theta2))/100000]
[ - sin(theta6)*(cos(theta1)*cos(theta4) - sin(theta4)*(sin(theta1)*sin(theta2)*sin(theta3) - cos(theta2)*cos(theta3)*sin(theta1))) - cos(theta6)*(cos(theta5)*(cos(theta1)*sin(theta4) + cos(theta4)*(sin(theta1)*sin(theta2)*sin(theta3) - cos(theta2)*cos(theta3)*sin(theta1))) + sin(theta5)*(cos(theta2)*sin(theta1)*sin(theta3) + cos(theta3)*sin(theta1)*sin(theta2))), sin(theta6)*(cos(theta5)*(cos(theta1)*sin(theta4) + cos(theta4)*(sin(theta1)*sin(theta2)*sin(theta3) - cos(theta2)*cos(theta3)*sin(theta1))) + sin(theta5)*(cos(theta2)*sin(theta1)*sin(theta3) + cos(theta3)*sin(theta1)*sin(theta2))) - cos(theta6)*(cos(theta1)*cos(theta4) - sin(theta4)*(sin(theta1)*sin(theta2)*sin(theta3) - cos(theta2)*cos(theta3)*sin(theta1))), cos(theta5)*(cos(theta2)*sin(theta1)*sin(theta3) + cos(theta3)*sin(theta1)*sin(theta2)) - sin(theta5)*(cos(theta1)*sin(theta4) + cos(theta4)*(sin(theta1)*sin(theta2)*sin(theta3) - cos(theta2)*cos(theta3)*sin(theta1))), (14909*cos(theta1))/100000 + (2159*cos(theta2)*sin(theta1))/5000 - (43307*cos(theta2)*sin(theta1)*sin(theta3))/100000 - (43307*cos(theta3)*sin(theta1)*sin(theta2))/100000 - (127*sin(theta1)*sin(theta2)*sin(theta3))/6250 + (127*cos(theta2)*cos(theta3)*sin(theta1))/6250]
[ sin(theta4)*sin(theta6)*(cos(theta2)*sin(theta3) + cos(theta3)*sin(theta2)) - cos(theta6)*(sin(theta5)*(cos(theta2)*cos(theta3) - sin(theta2)*sin(theta3)) + cos(theta4)*cos(theta5)*(cos(theta2)*sin(theta3) + cos(theta3)*sin(theta2))), sin(theta6)*(sin(theta5)*(cos(theta2)*cos(theta3) - sin(theta2)*sin(theta3)) + cos(theta4)*cos(theta5)*(cos(theta2)*sin(theta3) + cos(theta3)*sin(theta2))) + cos(theta6)*sin(theta4)*(cos(theta2)*sin(theta3) + cos(theta3)*sin(theta2)), cos(theta5)*(cos(theta2)*cos(theta3) - sin(theta2)*sin(theta3)) - cos(theta4)*sin(theta5)*(cos(theta2)*sin(theta3) + cos(theta3)*sin(theta2)), (43307*sin(theta2)*sin(theta3))/100000 - (43307*cos(theta2)*cos(theta3))/100000 - (127*cos(theta2)*sin(theta3))/6250 - (127*cos(theta3)*sin(theta2))/6250 - (2159*sin(theta2))/5000]
[ 0, 0, 0, 1]
- 1
- 2
- 3
- 4
- 5
- 6
化简:
>> simplify(T06)
ans =
[ sin(theta6)*(cos(theta4)*sin(theta1) + sin(theta4)*(cos(theta1)*sin(theta2)*sin(theta3) - cos(theta1)*cos(theta2)*cos(theta3))) + cos(theta6)*(cos(theta5)*(sin(theta1)*sin(theta4) - cos(theta4)*(cos(theta1)*sin(theta2)*sin(theta3) - cos(theta1)*cos(theta2)*cos(theta3))) - sin(theta5)*(cos(theta1)*cos(theta2)*sin(theta3) + cos(theta1)*cos(theta3)*sin(theta2))), cos(theta6)*(cos(theta4)*sin(theta1) + sin(theta4)*(cos(theta1)*sin(theta2)*sin(theta3) - cos(theta1)*cos(theta2)*cos(theta3))) - sin(theta6)*(cos(theta5)*(sin(theta1)*sin(theta4) - cos(theta4)*(cos(theta1)*sin(theta2)*sin(theta3) - cos(theta1)*cos(theta2)*cos(theta3))) - sin(theta5)*(cos(theta1)*cos(theta2)*sin(theta3) + cos(theta1)*cos(theta3)*sin(theta2))), sin(theta5)*(sin(theta1)*sin(theta4) - cos(theta4)*(cos(theta1)*sin(theta2)*sin(theta3) - cos(theta1)*cos(theta2)*cos(theta3))) + cos(theta5)*(cos(theta1)*cos(theta2)*sin(theta3) + cos(theta1)*cos(theta3)*sin(theta2)), (2159*cos(theta1)*cos(theta2))/5000 - (14909*sin(theta1))/100000 - (127*cos(theta1)*sin(theta2)*sin(theta3))/6250 + (127*cos(theta1)*cos(theta2)*cos(theta3))/6250 - (43307*cos(theta1)*cos(theta2)*sin(theta3))/100000 - (43307*cos(theta1)*cos(theta3)*sin(theta2))/100000]
[ - sin(theta6)*(cos(theta1)*cos(theta4) - sin(theta4)*(sin(theta1)*sin(theta2)*sin(theta3) - cos(theta2)*cos(theta3)*sin(theta1))) - cos(theta6)*(cos(theta5)*(cos(theta1)*sin(theta4) + cos(theta4)*(sin(theta1)*sin(theta2)*sin(theta3) - cos(theta2)*cos(theta3)*sin(theta1))) + sin(theta5)*(cos(theta2)*sin(theta1)*sin(theta3) + cos(theta3)*sin(theta1)*sin(theta2))), sin(theta6)*(cos(theta5)*(cos(theta1)*sin(theta4) + cos(theta4)*(sin(theta1)*sin(theta2)*sin(theta3) - cos(theta2)*cos(theta3)*sin(theta1))) + sin(theta5)*(cos(theta2)*sin(theta1)*sin(theta3) + cos(theta3)*sin(theta1)*sin(theta2))) - cos(theta6)*(cos(theta1)*cos(theta4) - sin(theta4)*(sin(theta1)*sin(theta2)*sin(theta3) - cos(theta2)*cos(theta3)*sin(theta1))), cos(theta5)*(cos(theta2)*sin(theta1)*sin(theta3) + cos(theta3)*sin(theta1)*sin(theta2)) - sin(theta5)*(cos(theta1)*sin(theta4) + cos(theta4)*(sin(theta1)*sin(theta2)*sin(theta3) - cos(theta2)*cos(theta3)*sin(theta1))), (14909*cos(theta1))/100000 + (2159*cos(theta2)*sin(theta1))/5000 - (43307*cos(theta2)*sin(theta1)*sin(theta3))/100000 - (43307*cos(theta3)*sin(theta1)*sin(theta2))/100000 - (127*sin(theta1)*sin(theta2)*sin(theta3))/6250 + (127*cos(theta2)*cos(theta3)*sin(theta1))/6250]
[ sin(theta2 + theta3)*sin(theta4)*sin(theta6) - cos(theta6)*(cos(theta2 + theta3)*sin(theta5) + sin(theta2 + theta3)*cos(theta4)*cos(theta5)), sin(theta6)*(cos(theta2 + theta3)*sin(theta5) + sin(theta2 + theta3)*cos(theta4)*cos(theta5)) + sin(theta2 + theta3)*cos(theta6)*sin(theta4), cos(theta2 + theta3)*cos(theta5) - sin(theta2 + theta3)*cos(theta4)*sin(theta5), - (2159*sin(theta2))/5000 - (127*116537^(1/2)*cos(theta2 + theta3 - atan(16/341)))/100000]
[ 0, 0, 0, 1]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
正运动学方程一般写成这样:

简洁表达成这样:

4.2 正运动学方程正确性验证
验证自己编写的正运动学函数:
% 用自己编写的正运动学函数求解
T06 = puma560_fk(-pi/2,-pi/2,0,0,0,0)
% 用机器人工具箱提供的函数求解
T0_6 = p560.fkine([-pi/2 -pi/2 0 0 0 0])
- 1
- 2
- 3
- 4
对比运算结果,正运动学无误:
T06 =
0.0000 -1.0000 -0.0000 0.1491
-0.0000 -0.0000 1.0000 -0.4331
1.0000 0 0.0000 0.4521
0 0 0 1.0000
T0_6 =
0 -1 0 0.1491
0 0 -1 -0.4331
1 0 0 0.4521
0 0 0 1
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
4.3 求解逆运动学方程

求解按照《机器人学—蔡自兴》的步骤结合MATLAB就可以了,现在根据求解出来的各个关节角将逆运动学求解封装成函数:
function theta_Med=puma560_ik(T) % a--连杆长度,d--连杆偏移量 a2=0.4318; a3=0.02032; d2=0.14909; d4=0.43307; nx=T(1,1); ny=T(2,1); nz=T(3,1); ox=T(1,2); oy=T(2,2); oz=T(3,2); ax=T(1,3); ay=T(2,3); az=T(3,3); px=T(1,4); py=T(2,4); pz=T(3,4); % 为方便计算,定义的m系列向量 % 求解关节角1 theta1_1 = atan2(py,px)-atan2(d2,sqrt(px^2+py^2-d2^2)); theta1_2 = atan2(py,px)-atan2(d2,-sqrt(px^2+py^2-d2^2)); % 求解关节角3 m3_1 = (px^2+py^2+pz^2-a2^2-a3^2-d2^2-d4^2)/(2*a2); theta3_1 = atan2(a3,d4)-atan2(m3_1,sqrt(a3^2+d4^2-m3_1^2)); theta3_2 = atan2(a3,d4)-atan2(m3_1,-sqrt(a3^2+d4^2-m3_1^2)); % 求解关节角2 ms2_1 = -((a3+a2*cos(theta3_1))*pz)+(cos(theta1_1)*px+sin(theta1_1)*py)*(a2*sin(theta3_1)-d4); mc2_1 = (-d4+a2*sin(theta3_1))*pz+(cos(theta1_1)*px+sin(theta1_1)*py)*(a2*cos(theta3_1)+a3); theta23_1 = atan2(ms2_1,mc2_1); theta2_1 = theta23_1 - theta3_1; ms2_2 = -((a3+a2*cos(theta3_1))*pz)+(cos(theta1_2)*px+sin(theta1_2)*py)*(a2*sin(theta3_1)-d4); mc2_2 = (-d4+a2*sin(theta3_1))*pz+(cos(theta1_2)*px+sin(theta1_2)*py)*(a2*cos(theta3_1)+a3); theta23_2 = atan2(ms2_2,mc2_2); theta2_2 = theta23_2 - theta3_1; ms2_3 = -((a3+a2*cos(theta3_2))*pz)+(cos(theta1_1)*px+sin(theta1_1)*py)*(a2*sin(theta3_2)-d4); mc2_3 = (-d4+a2*sin(theta3_2))*pz+(cos(theta1_1)*px+sin(theta1_1)*py)*(a2*cos(theta3_2)+a3); theta23_3 = atan2(ms2_3,mc2_3); theta2_3 = theta23_3 - theta3_2; ms2_4 = -((a3+a2*cos(theta3_2))*pz)+(cos(theta1_2)*px+sin(theta1_2)*py)*(a2*sin(theta3_2)-d4); mc2_4 = (-d4+a2*sin(theta3_2))*pz+(cos(theta1_2)*px+sin(theta1_2)*py)*(a2*cos(theta3_2)+a3); theta23_4 = atan2(ms2_4,mc2_4); theta2_4 = theta23_4 - theta3_2; % 求解关节角4 ms4_1=-ax*sin(theta1_1)+ay*cos(theta1_1); mc4_1=-ax*cos(theta1_1)*cos(theta23_1)-ay*sin(theta1_1)*cos(theta23_1)+az*sin(theta23_1); theta4_1=atan2(ms4_1,mc4_1); ms4_2=-ax*sin(theta1_2)+ay*cos(theta1_2); mc4_2=-ax*cos(theta1_2)*cos(theta23_2)-ay*sin(theta1_2)*cos(theta23_2)+az*sin(theta23_2); theta4_2=atan2(ms4_2,mc4_2); ms4_3=-ax*sin(theta1_1)+ay*cos(theta1_1); mc4_3=-ax*cos(theta1_1)*cos(theta23_3)-ay*sin(theta1_1)*cos(theta23_3)+az*sin(theta23_3); theta4_3=atan2(ms4_3,mc4_3); ms4_4=-ax*sin(theta1_2)+ay*cos(theta1_2); mc4_4=-ax*cos(theta1_2)*cos(theta23_4)-ay*sin(theta1_2)*cos(theta23_4)+az*sin(theta23_4); theta4_4=atan2(ms4_4,mc4_4); % 求解关节角5 ms5_1=-ax*(cos(theta1_1)*cos(theta23_1)*cos(theta4_1)+sin(theta1_1)*sin(theta4_1))-ay*(sin(theta1_1)*cos(theta23_1)*cos(theta4_1)-cos(theta1_1)*sin(theta4_1))+az*(sin(theta23_1)*cos(theta4_1)); mc5_1= ax*(-cos(theta1_1)*sin(theta23_1))+ay*(-sin(theta1_1)*sin(theta23_1))+az*(-cos(theta23_1)); theta5_1=atan2(ms5_1,mc5_1); ms5_2=-ax*(cos(theta1_2)*cos(theta23_2)*cos(theta4_2)+sin(theta1_2)*sin(theta4_2))-ay*(sin(theta1_2)*cos(theta23_2)*cos(theta4_2)-cos(theta1_2)*sin(theta4_2))+az*(sin(theta23_2)*cos(theta4_2)); mc5_2= ax*(-cos(theta1_2)*sin(theta23_2))+ay*(-sin(theta1_2)*sin(theta23_2))+az*(-cos(theta23_2)); theta5_2=atan2(ms5_2,mc5_2); ms5_3=-ax*(cos(theta1_1)*cos(theta23_3)*cos(theta4_3)+sin(theta1_1)*sin(theta4_3))-ay*(sin(theta1_1)*cos(theta23_3)*cos(theta4_3)-cos(theta1_1)*sin(theta4_3))+az*(sin(theta23_3)*cos(theta4_3)); mc5_3= ax*(-cos(theta1_1)*sin(theta23_3))+ay*(-sin(theta1_1)*sin(theta23_3))+az*(-cos(theta23_3)); theta5_3=atan2(ms5_3,mc5_3); ms5_4=-ax*(cos(theta1_2)*cos(theta23_4)*cos(theta4_4)+sin(theta1_2)*sin(theta4_4))-ay*(sin(theta1_2)*cos(theta23_4)*cos(theta4_4)-cos(theta1_2)*sin(theta4_4))+az*(sin(theta23_4)*cos(theta4_4)); mc5_4= ax*(-cos(theta1_2)*sin(theta23_4))+ay*(-sin(theta1_2)*sin(theta23_4))+az*(-cos(theta23_4)); theta5_4=atan2(ms5_4,mc5_4); % 求解关节角6 ms6_1=-nx*(cos(theta1_1)*cos(theta23_1)*sin(theta4_1)-sin(theta1_1)*cos(theta4_1))-ny*(sin(theta1_1)*cos(theta23_1)*sin(theta4_1)+cos(theta1_1)*cos(theta4_1))+nz*(sin(theta23_1)*sin(theta4_1)); mc6_1= nx*(cos(theta1_1)*cos(theta23_1)*cos(theta4_1)+sin(theta1_1)*sin(theta4_1))*cos(theta5_1)-nx*cos(theta1_1)*sin(theta23_1)*sin(theta4_1)+ny*(sin(theta1_1)*cos(theta23_1)*cos(theta4_1)+cos(theta1_1)*sin(theta4_1))*cos(theta5_1)-ny*sin(theta1_1)*sin(theta23_1)*sin(theta5_1)-nz*(sin(theta23_1)*cos(theta4_1)*cos(theta5_1)+cos(theta23_1)*sin(theta5_1)); theta6_1=atan2(ms6_1,mc6_1); ms6_2=-nx*(cos(theta1_2)*cos(theta23_2)*sin(theta4_2)-sin(theta1_2)*cos(theta4_2))-ny*(sin(theta1_2)*cos(theta23_2)*sin(theta4_2)+cos(theta1_2)*cos(theta4_2))+nz*(sin(theta23_2)*sin(theta4_2)); mc6_2= nx*(cos(theta1_2)*cos(theta23_2)*cos(theta4_2)+sin(theta1_2)*sin(theta4_2))*cos(theta5_2)-nx*cos(theta1_2)*sin(theta23_2)*sin(theta4_2)+ny*(sin(theta1_2)*cos(theta23_2)*cos(theta4_2)+cos(theta1_2)*sin(theta4_2))*cos(theta5_2)-ny*sin(theta1_2)*sin(theta23_2)*sin(theta5_2)-nz*(sin(theta23_2)*cos(theta4_2)*cos(theta5_2)+cos(theta23_2)*sin(theta5_2)); theta6_2=atan2(ms6_2,mc6_2); ms6_3=-nx*(cos(theta1_1)*cos(theta23_3)*sin(theta4_3)-sin(theta1_1)*cos(theta4_3))-ny*(sin(theta1_1)*cos(theta23_3)*sin(theta4_3)+cos(theta1_1)*cos(theta4_3))+nz*(sin(theta23_3)*sin(theta4_3)); mc6_3= nx*(cos(theta1_1)*cos(theta23_3)*cos(theta4_3)+sin(theta1_1)*sin(theta4_3))*cos(theta5_3)-nx*cos(theta1_1)*sin(theta23_3)*sin(theta4_3)+ny*(sin(theta1_1)*cos(theta23_3)*cos(theta4_3)+cos(theta1_1)*sin(theta4_3))*cos(theta5_3)-ny*sin(theta1_1)*sin(theta23_3)*sin(theta5_3)-nz*(sin(theta23_3)*cos(theta4_3)*cos(theta5_3)+cos(theta23_3)*sin(theta5_3)); theta6_3=atan2(ms6_3,mc6_3); ms6_4=-nx*(cos(theta1_2)*cos(theta23_4)*sin(theta4_4)-sin(theta1_2)*cos(theta4_4))-ny*(sin(theta1_1)*cos(theta23_4)*sin(theta4_4)+cos(theta1_2)*cos(theta4_4))+nz*(sin(theta23_4)*sin(theta4_4)); mc6_4= nx*(cos(theta1_2)*cos(theta23_4)*cos(theta4_4)+sin(theta1_2)*sin(theta4_4))*cos(theta5_4)-nx*cos(theta1_2)*sin(theta23_4)*sin(theta4_4)+ny*(sin(theta1_2)*cos(theta23_4)*cos(theta4_4)+cos(theta1_2)*sin(theta4_4))*cos(theta5_1)-ny*sin(theta1_2)*sin(theta23_4)*sin(theta5_4)-nz*(sin(theta23_4)*cos(theta4_4)*cos(theta5_4)+cos(theta23_4)*sin(theta5_4)); theta6_4=atan2(ms6_4,mc6_4); % 整理得到4组运动学非奇异逆解 theta_Med_1 = [ theta1_1,theta2_1,theta3_1,theta4_1,theta5_1,theta6_1; theta1_2,theta2_2,theta3_1,theta4_2,theta5_2,theta6_2; theta1_1,theta2_3,theta3_2,theta4_3,theta5_3,theta6_3; theta1_2,theta2_4,theta3_2,theta4_4,theta5_4,theta6_4; ]; % 将操作关节‘翻转’可得到另外4组解 theta_Med_2 = ... [ theta1_1,theta2_1,theta3_1,theta4_1+pi,-theta5_1,theta6_1+pi; theta1_2,theta2_2,theta3_1,theta4_2+pi,-theta5_2,theta6_2+pi; theta1_1,theta2_3,theta3_2,theta4_3+pi,-theta5_3,theta6_3+pi; theta1_2,theta2_4,theta3_2,theta4_4+pi,-theta5_4,theta6_4+pi; ]; theta_Med=[theta_Med_1;theta_Med_2]; end
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
4.4 逆运动学方程正确性验证
%用自己编写的逆运动学函数求解
T06 = kinematics([-pi/2 -pi/2 0 0 0 0])
theta_med = puma560_ik(T06)
- 1
- 2
- 3
8组逆运动学解
theta_med =
-1.5708 -1.5708 -0.0000 0 0 0
-4.0493 -3.0986 -0.0000 2.4780 1.6047 -0.0265
-1.5708 -0.0430 -3.0478 0 1.5201 0
-4.0493 4.7124 -3.0478 1.6901 0.6687 1.4192
-1.5708 -1.5708 -0.0000 3.1416 0 3.1416
-4.0493 -3.0986 -0.0000 5.6196 -1.6047 3.1151
-1.5708 -0.0430 -3.0478 3.1416 -1.5201 3.1416
-4.0493 4.7124 -3.0478 4.8317 -0.6687 4.5608
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
其中第一组解就是我想要的结果:
-1.5708 -1.5708 -0.0000 0 0 0
- 1
4.5 雅克比矩阵
机器人雅克比矩阵可以联系机器人末端操作空间速度和关节空间速度,已知关节空间速度,利用雅克比矩阵,可以得到操作空间的速度,再结合逆过程,就可以实现速度模式控制机器人,从而初步实现平滑运动。
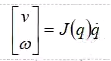
公式中,v 和 w 是笛卡尔空间中的速度和角速度,并且 q(dot) 是一个关节速度向量。
%练习使用雅克比矩阵求解函数
qn = [0 0.7854 3.1416 0 0.7854 0];
%jacob0()求解的是将关节速度映射到世界坐标系中的末端执行器空间速度
p560.jacob0(qn)
%jaconb()求解的是将关节速度映射到工具坐标系中的末端执行器空间速度
p560.jacobe(qn)
- 1
- 2
- 3
- 4
- 5
- 6
结果:
jacob0 = -0.1491 0.0153 0.3206 0 0 0 0.5972 0.0000 0.0000 0 0 0 -0.0000 -0.5972 -0.2919 0 0 0 -0.0000 0 0 0.7071 0 1.0000 0 1.0000 1.0000 0.0000 1.0000 0.0000 1.0000 0.0000 0.0000 0.7071 0.0000 -0.0000 jacobn = -0.0000 -0.5972 -0.2919 0 0 0 -0.5972 0.0000 0.0000 0 0 0 -0.1491 0.0153 0.3206 0 0 0 1.0000 0 0 0.7071 0 0 -0.0000 -1.0000 -1.0000 -0.0000 -1.0000 0 -0.0000 0.0000 0.0000 0.7071 0.0000 1.0000
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
5. 参考资料
- 基于Matlab的PUMA 560运动学与轨迹规划仿真
- 博士论文《协作机器人零力控制与碰撞检测技术研究_陈赛旋》,有关于正逆运动学求解的详细推导过程
- 论文《六自由度模块化机械臂的逆运动学分析》
声明:本文内容由网友自发贡献,不代表【wpsshop博客】立场,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:https://www.wpsshop.cn/w/我家小花儿/article/detail/262713
推荐阅读
相关标签



