图神经网络简介，什么是图神经网络，GNN

目录

什么是图？

 二、怎么把一些内容表示成图

2.1 怎么把图片表示成图

 2.2 将一句话表示成图

 2.3 其他信息转换成图的例子

 2.3.1 分子结构表示成图

2.3.2 社会人物关系表示成图

2.3.3 其他可以表示成图的信息

三、哪些类型的问题有图结构数据

3.1 图层面的任务

 3.2 节点层面的任务

3.3 边层面的任务

四、神经网络用在图上面的挑战

 五、图神经网络 GNN

5.1 什么是GNN？

5.2 最简单的GNN层

5.3 通过池化信息对GNN预测

5.4 Passing messages between parts of the graph

5.5 Learning edge representations

5.6 加入全局信息

六、 GNN playground

 6.1 一些GNN的设计经验

6.1.1 顶点、边和全局信息的向量长度

6.1.2 GNN的层数

6.1.3 聚合函数

6.1.4 信息传递

七、 GNN相关的技术

7.1 其他类型的图

7.2 GNN中的采样和bath

7.3 Inductive biases

7.4 不同汇聚操作的比较

7.4 GCN作为子图的函数近似

---

distill博客：A Gentle Introduction to Graph Neural Networks (distill.pub)

什么是图？

图是由一些点和一些线构成的，能表示一些实体之间的关系，图中的点就是实体，线就是实体间的关系。如下图，v就是顶点，e是边，u是整张图。attrinbutes是信息的意思，每个点、每条边、每个图都是有信息的。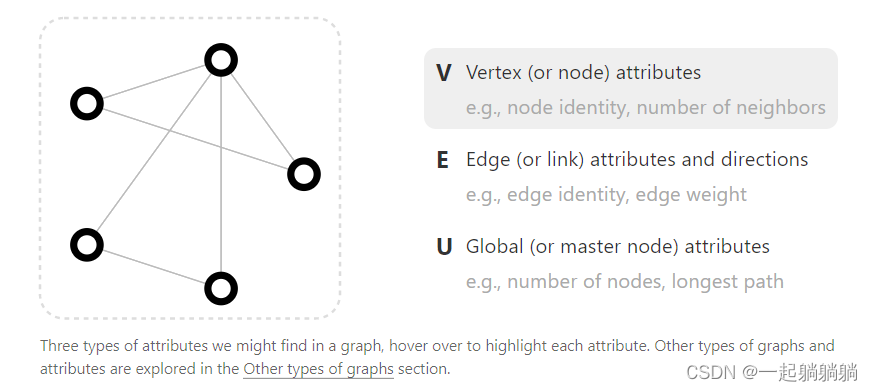

怎么表示一张图，可以参考下面这个例子

每个顶点、边和整张图都可以用一个向量来表示，在这个例子中，顶点的向量有六个值，柱体的高矮就表示该值的大小，每条边用一个长为8的向量来表示，全局用一个长为5的向量来表示

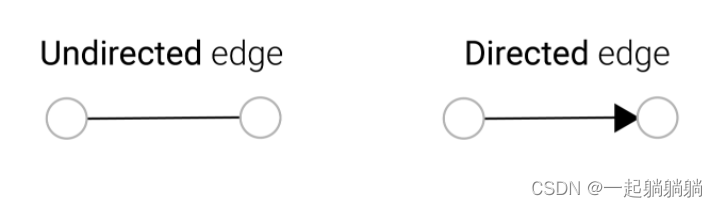
图分为两种，一种是有向图，一种是无向图。有向图就是单边关系图，比如A暗恋B，而B并没有暗恋A，这就是一个单边关系；无向图就是互为这种关系，比如说情侣，双方互相喜欢。

 二、怎么把一些内容表示成图

2.1 怎么把图片表示成图

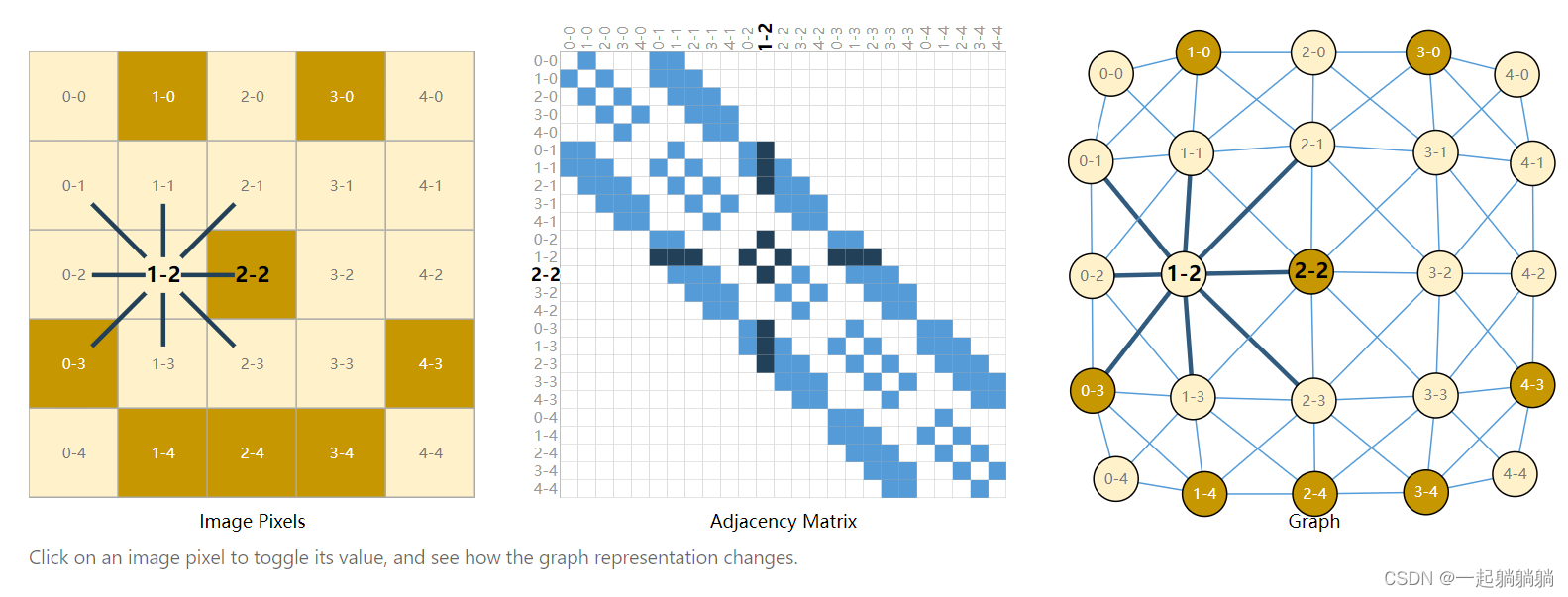
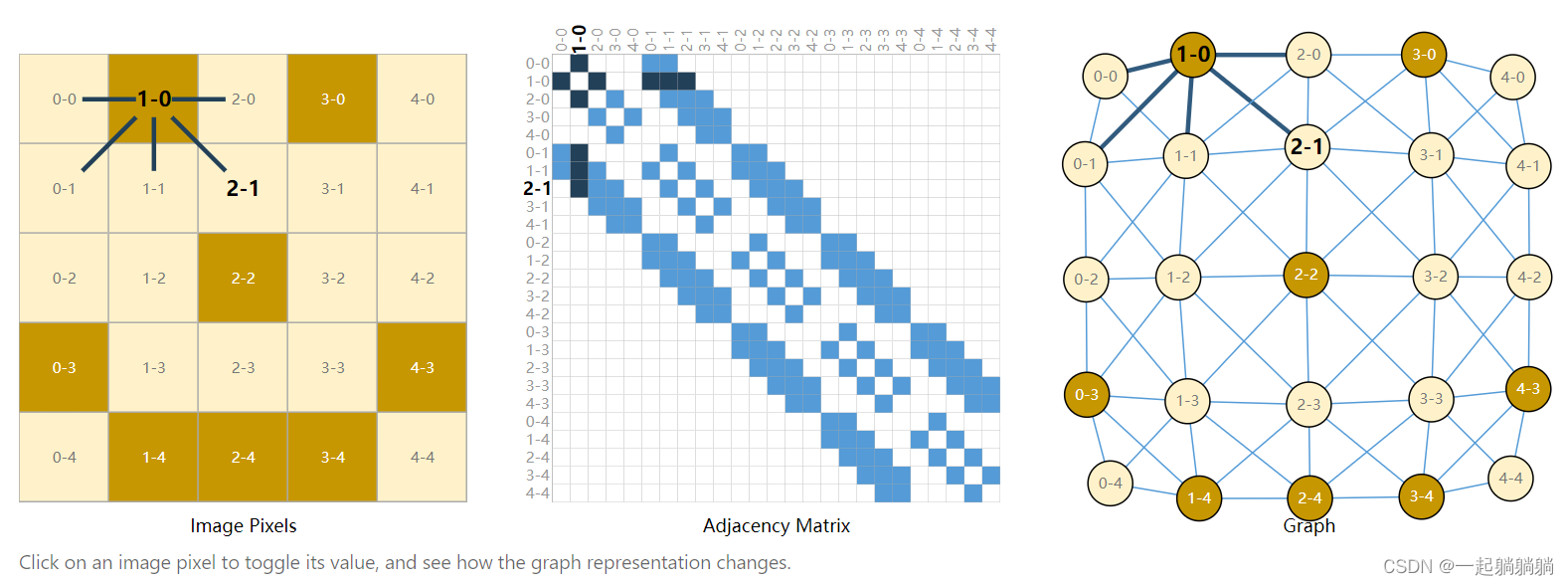
比如说一张图片可以表示为一个244*244*3的tensor，244*244个像素，3个rgb通道。就可以像下图这样表示，点表示的是像素，边表示的是像素间的邻接关系，建议大家去博客看一看，可以互动，更为直观。

 

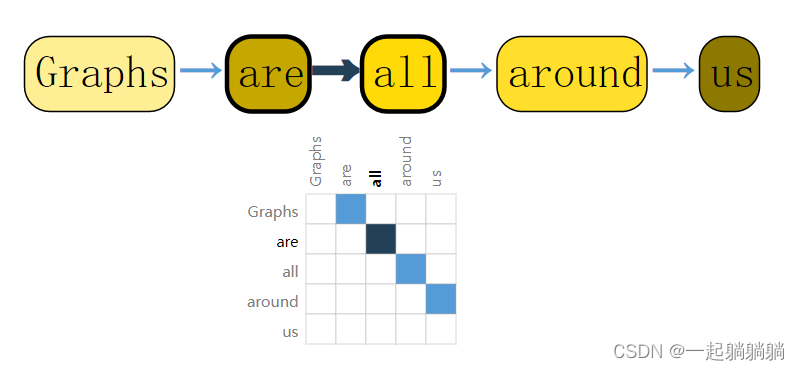
 2.2 将一句话表示成图

句子中的每个单词可以表示成一个节点，有向边表示这些单词的链接关系.

 2.3 其他信息转换成图的例子

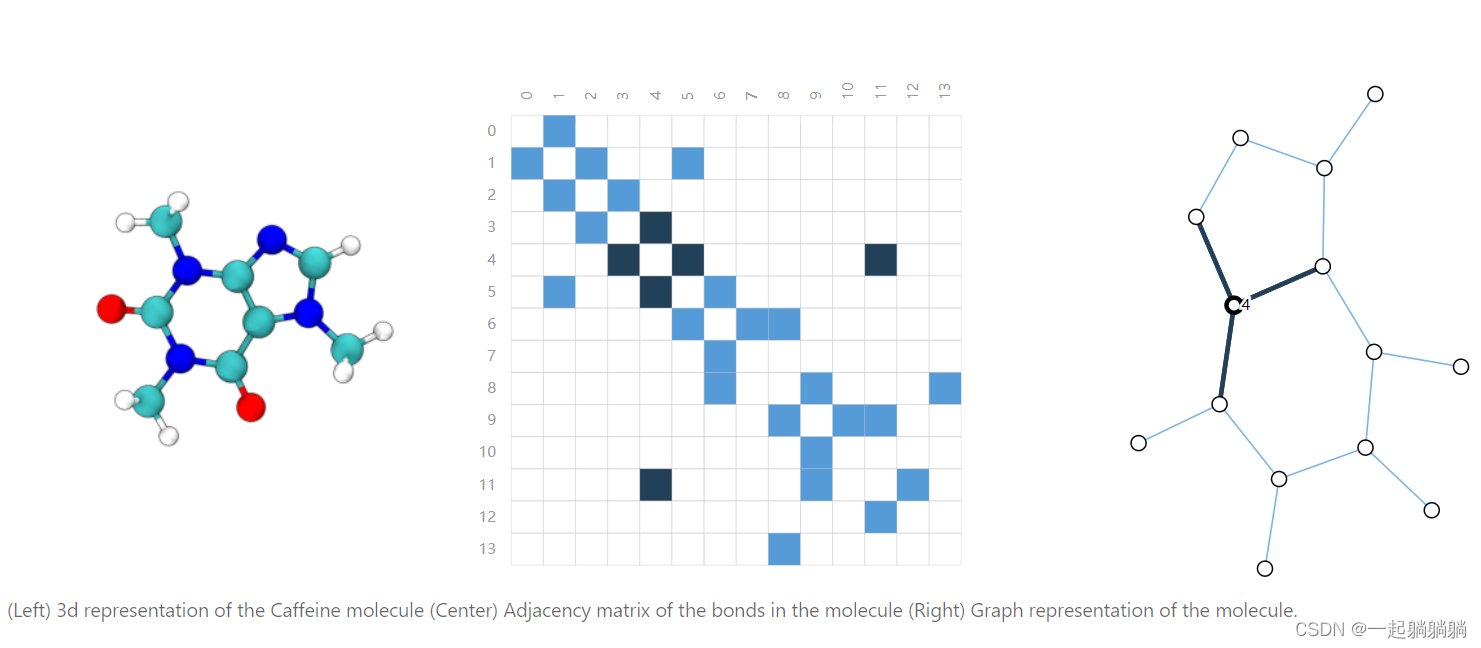
 2.3.1 分子结构表示成图

每个原子表示成一个节点，原子间的连接键表示成一个边

2.3.2 社会人物关系表示成图

比如将“Othello”中的人物关系表示成图，点代表人物，边代表这两个人物同时在一个场景中出现过

再比如，有一个武术培训班，两个老师和很多学生，点表示人，边表示两者间做过比赛

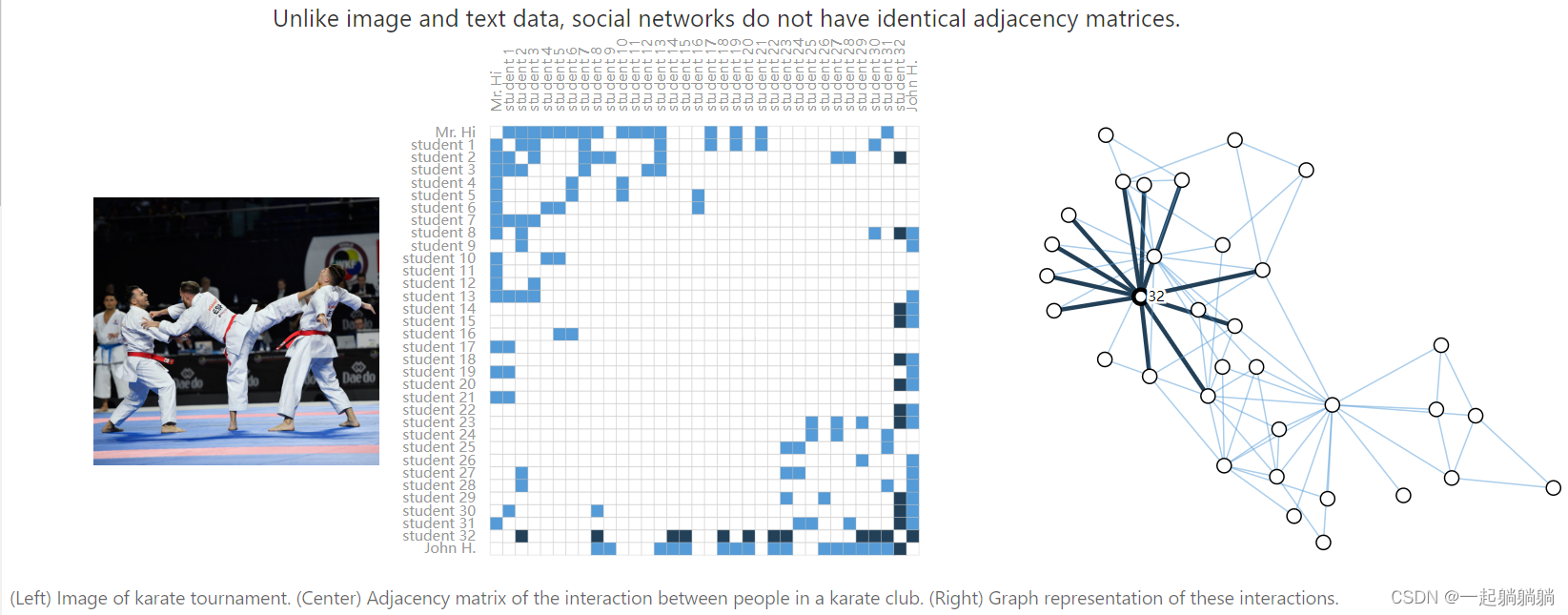
2.3.3 其他可以表示成图的信息

作为图表的引用网络。科学家在发表论文时经常引用其他科学家的工作。我们可以将这些引文网络可视化为一个图表，其中每篇论文都是一个节点，每个有向边缘都是一篇论文和另一篇论文之间的引用。此外，我们可以将有关每篇论文的信息添加到每个节点中，例如摘要的词嵌入。（请参见 [9]、 [10]、 [11]）。

其他示例。在计算机视觉中，我们有时想要在视觉场景中标记对象。然后，我们可以通过将这些对象视为节点，将它们的关系视为边缘来构建图形。机器学习模型、编程代码[12]和数字方程式[13]也可以表述为图形，其中变量是节点，边缘是将这些变量作为输入和输出的操作。您可能会在其中一些上下文中看到术语“数据流图”。

一些在实际中碰到的图的大小

三、哪些类型的问题有图结构数据

 图上面有三种常规类型的预测任务：图层面，节点层面，边层面。

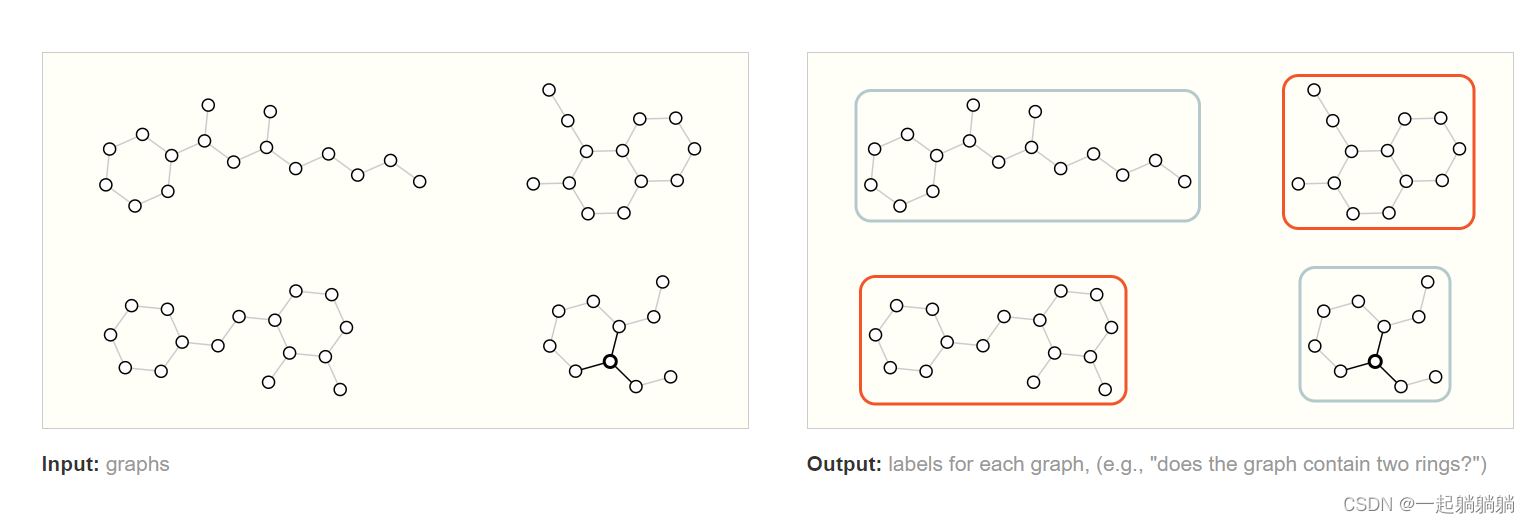
3.1 图层面的任务

在这个任务中，目标是预测图形的属性，辨别图中是否含有两个环；该任务是分类问题

 3.2 节点层面的任务

前面武术班的例子，假如说两个老师决裂，根据该社交图预测学生会选择哪个老师

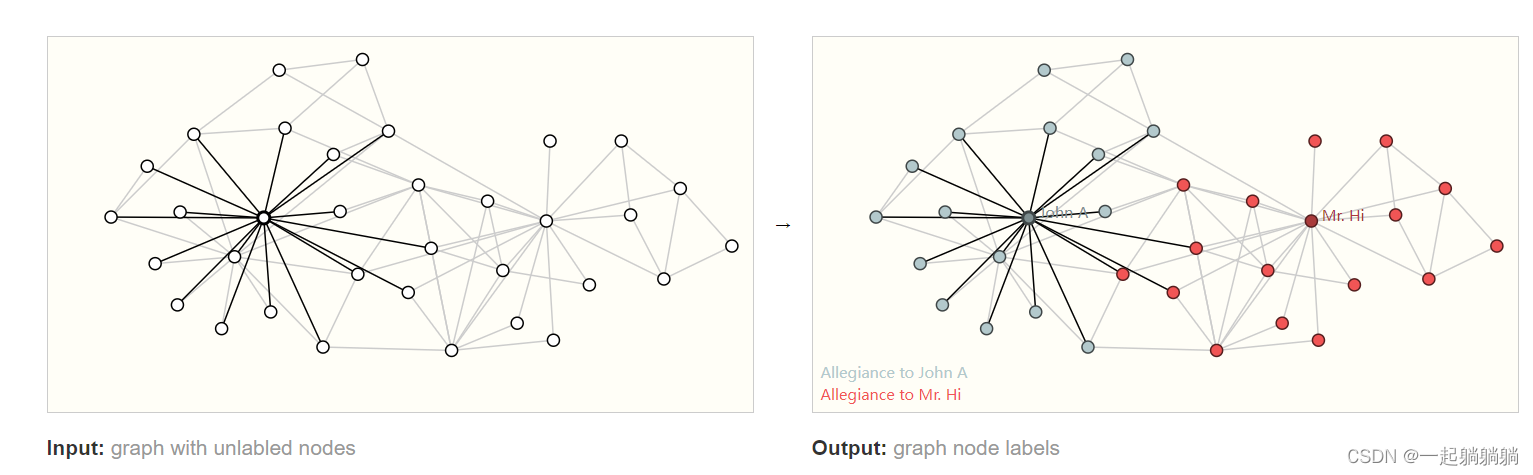
3.3 边层面的任务

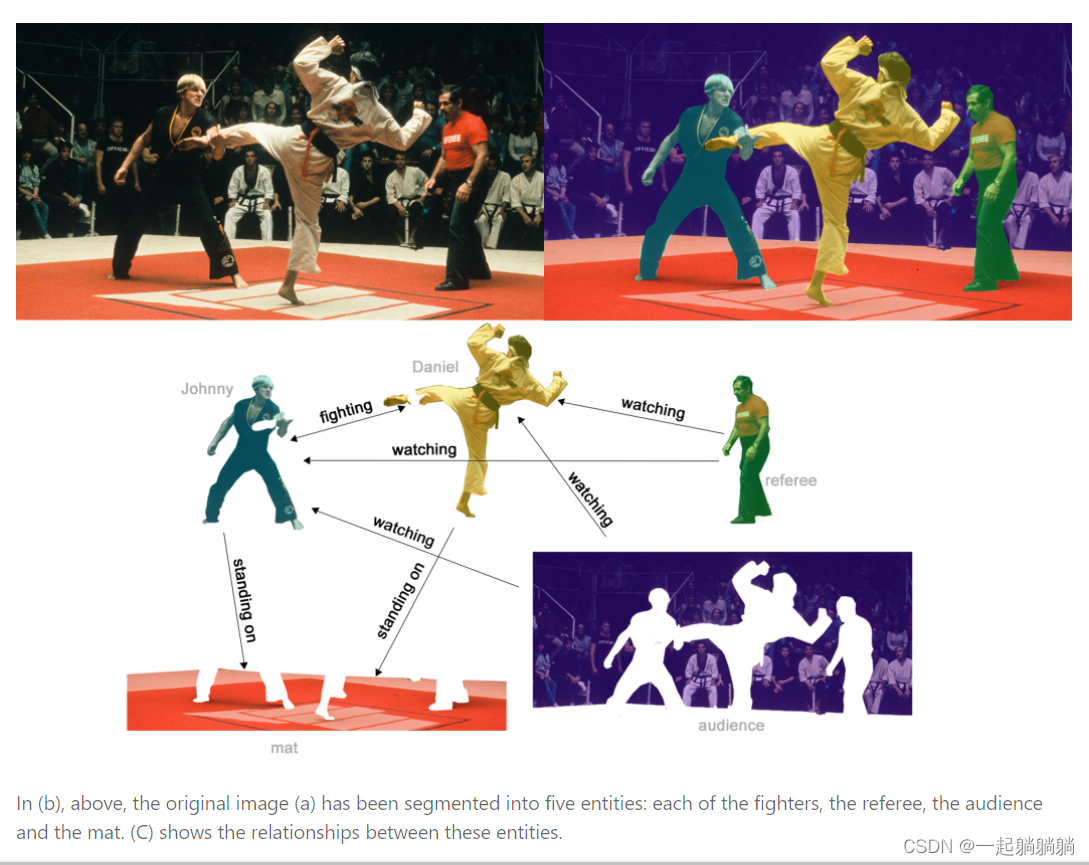
 先给出一张图片，然后经过语义分割将人物给分割出来，然后预测人物间的关系；这个图中顶点已经有了，相当于是预测边的属性。

 

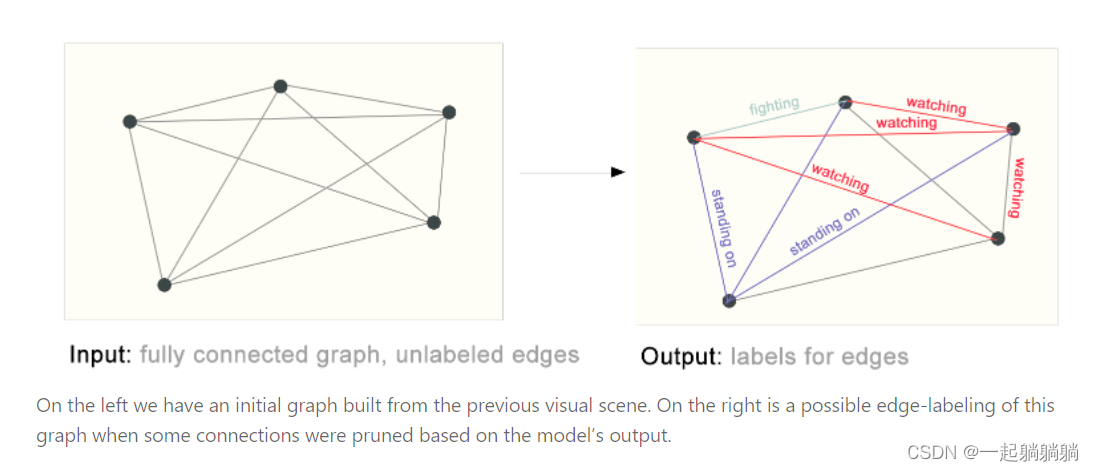
 这样就介绍了在图上面的三种不一样的任务问题。

四、神经网络用在图上面的挑战

核心问题是怎样表示图才能是和神经网络是兼容的。图上有四种信息：顶点的属性，边的属性，全局信息以及连接性（即为每条边连接的是哪两个顶点）。前三个信息都能用向量来表示，怎么表示连接性呢？

我们可以用邻接矩阵来表示，该矩阵会是一个方阵，但是有一些问题。这个矩阵可能会非常大而且很稀疏，在空间上效率低下，并且计算比较困难。另外将邻接矩阵的行或列的顺序进行交换不会改变其属性的。比如下面两张图都是前面“Othello"的人物关系图，看着不一样只是因为行和列的顺序不同，但是表示的信息是一样的。这就意味着如果你设计一个神经网络，无论你用下面两张图中的哪一张，都要保证得到的结果是一样的

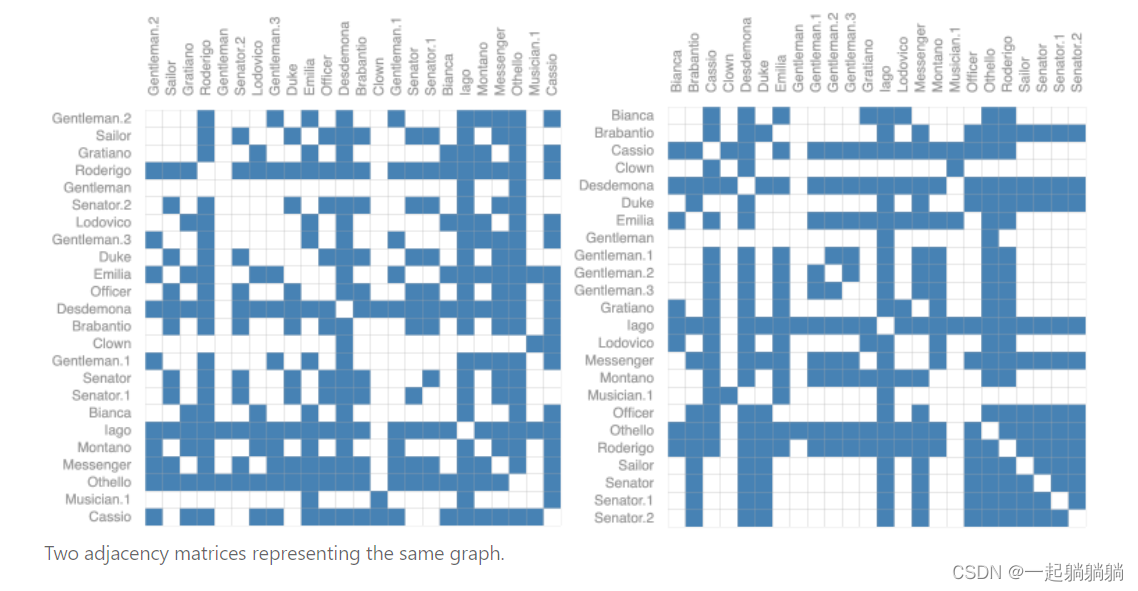
 比如下面这个例子，有四个顶点，下面是各种可能的排序

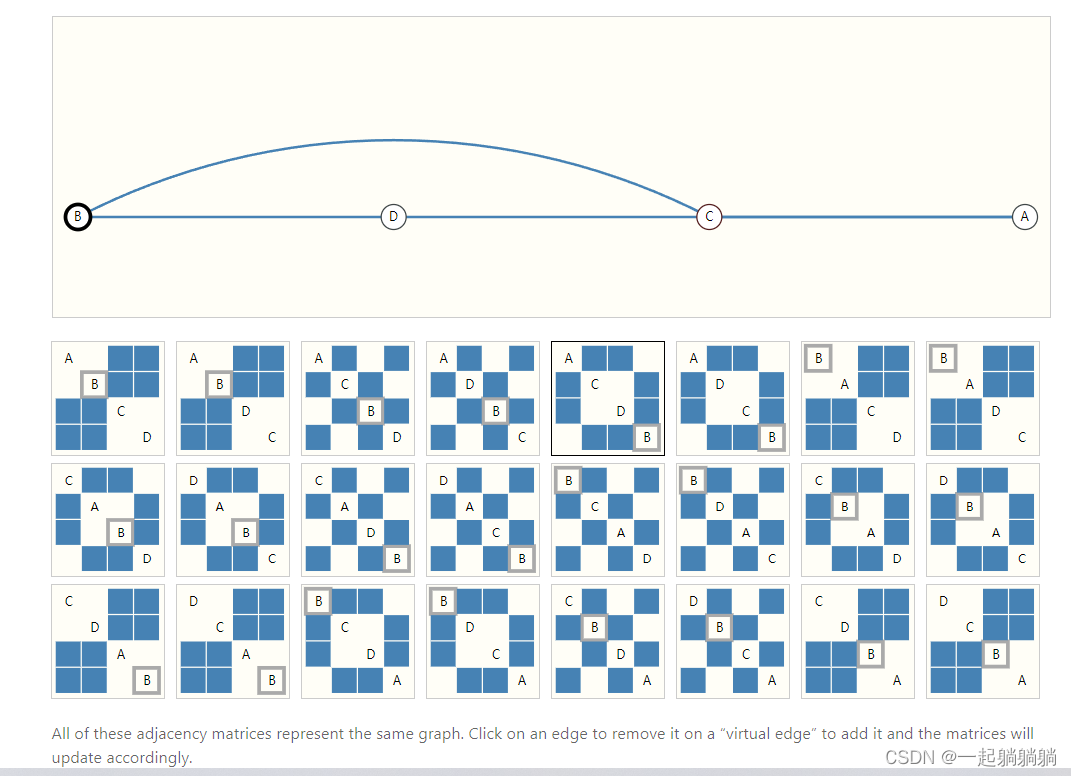
 如果既想高效的存储邻接矩阵，又想这个顺序不会影响神经网络的结果，就可以用邻接链表的方式来表示邻接矩阵。

比如下方这个，顶点，边和全局信息都用标量来表示，也可以用向量，连接性用邻接链表来表示，邻接链表的数量和边的数量是一致的，第i项表示的是第i条边连接的两个顶点；这样表示就很高效，而且不会受到顺序的影响。博客里面是可以改变数值和边的数量的，建议自己去博客玩一下。

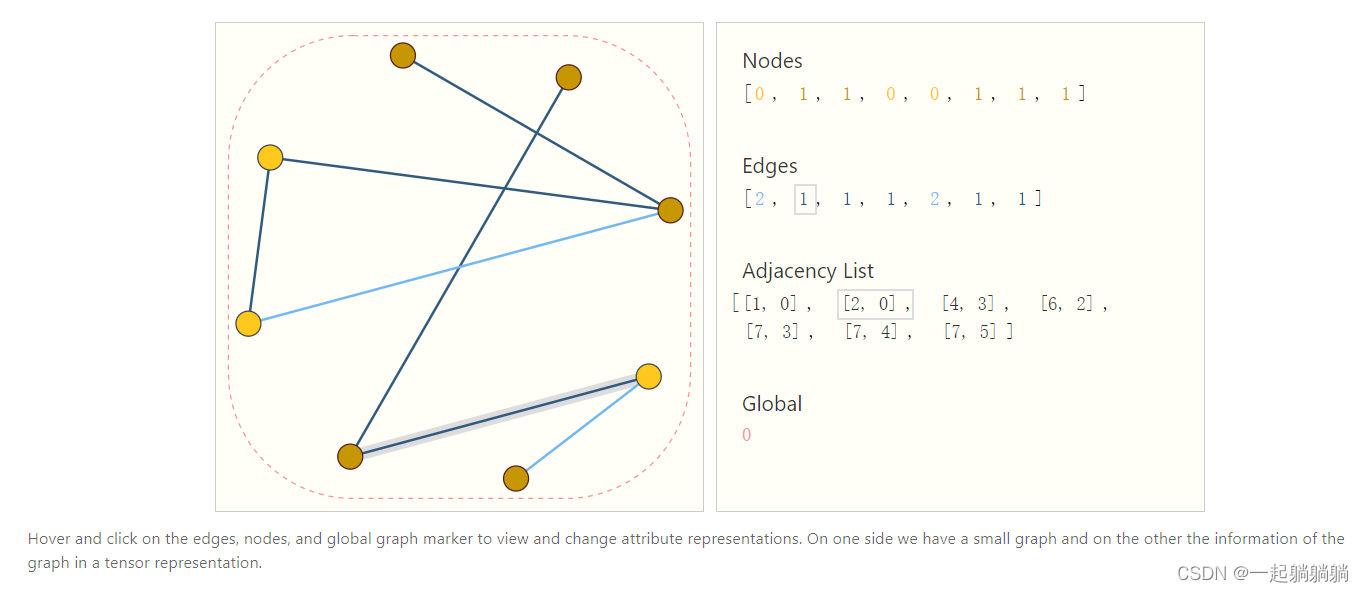
 五、图神经网络 GNN

5.1 什么是GNN？

 博客原话：

GNN is an optimizable transformation on all attributes of the graph (nodes, edges, global-context) that preserves graph symmetries (permutation invariances). 

GNN是对保持图对称性(排列不变性)的图的所有属性(节点、边、全局上下文)的可优化转换。对称信息指的是把这个顶点进行另外一个排序后，整个结果是不会变的。

这篇博客的GNN是用“信息传递神经网络”框架来搭建的，GNN的输入是一个图，输出也是一个图，它会对你的图的属性（点，边，全局信息）进行变换，但不会改变图的连接性，就是哪条边连接哪条顶点，这个信息是不会改变的。

5.2 最简单的GNN层

对顶点向量、边向量和全局向量分别构造一个多层感知机（MLP），输入的大小和输出的大小是相同的，这三个MLP就组成了一个GNN的层，输入是一个图，输出也是一个图，并且连接性不变。

满足了上文中对GNN的第一个要求，只对属性进行变换，并不改变图的结构；并且MLP是对每个向量独自作用，对样本前后顺序没有要求，所以也就满足了图的排列不变性，满足了第二个要求。

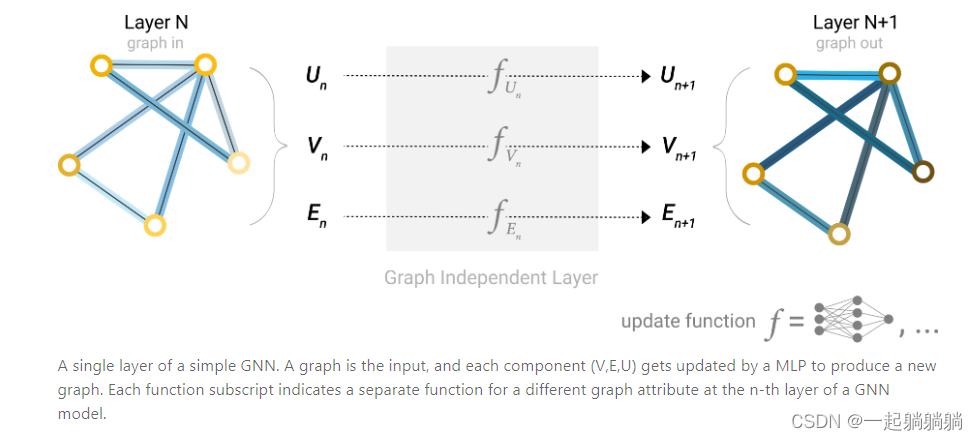
5.3 通过池化信息对GNN预测

考虑最简单的情况，例如前面讲到的武术馆的那张社交图。根据那张图来预测学生最终会选择哪个老师，顶点已经用向量来表示，可以直接加一个输出为2的全连接层。

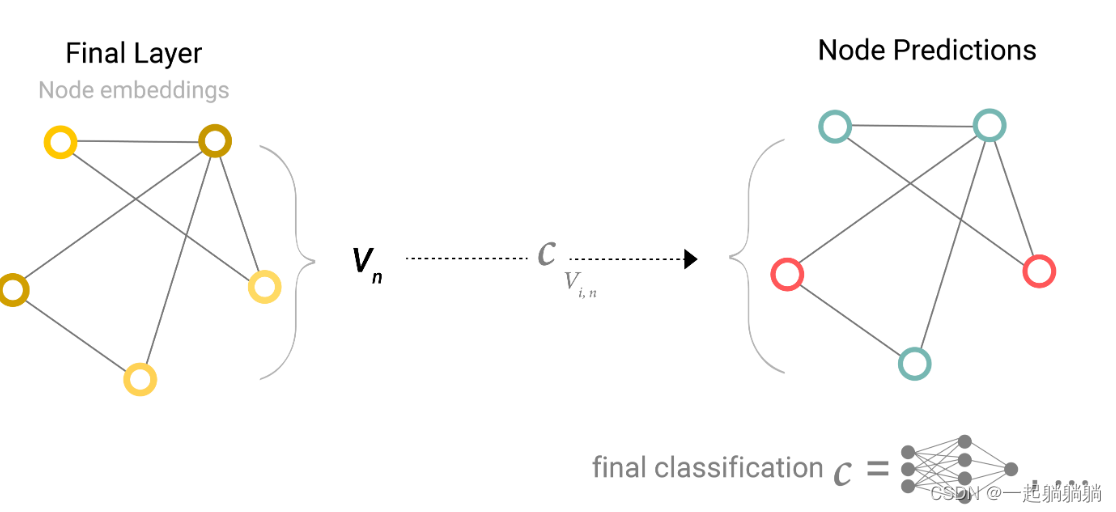
但是，如果顶点中没有信息，信息储存在边中，我们就需要一种收集边信息的方法，将其用作顶点预测。我们可以通过池化来完成这一步。

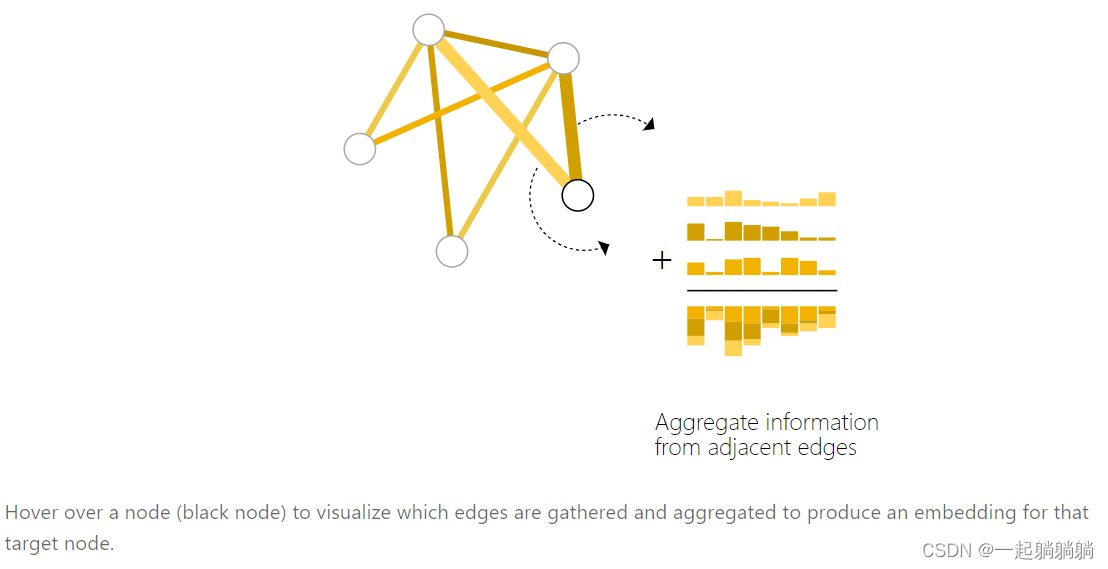如上图，该池化方法是将与该顶点相连接的边的信息与全局信息求和，用得到的信息做顶点预测。 

 

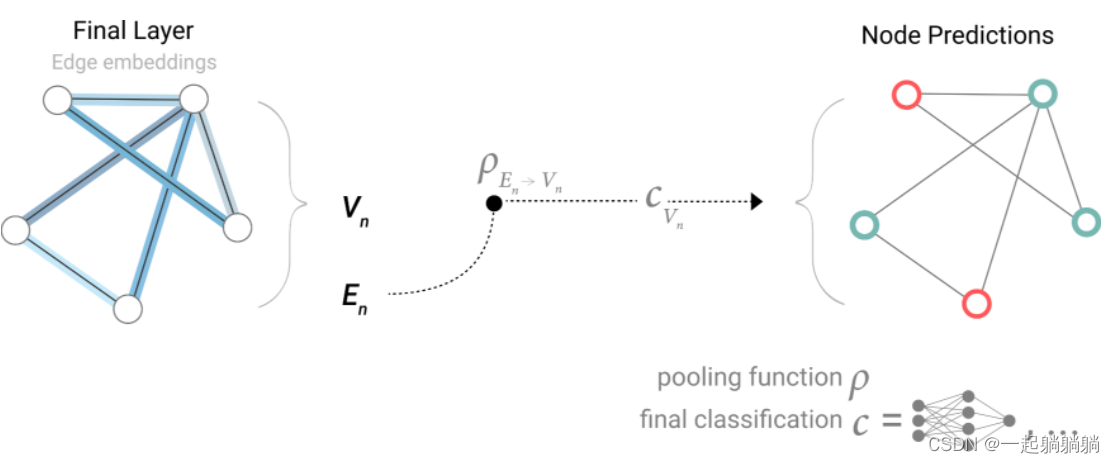
 同理也可以将此方法用作其他情况，比如用顶点信息池化来预测边，用顶点信息池化来预测全局属性等等。

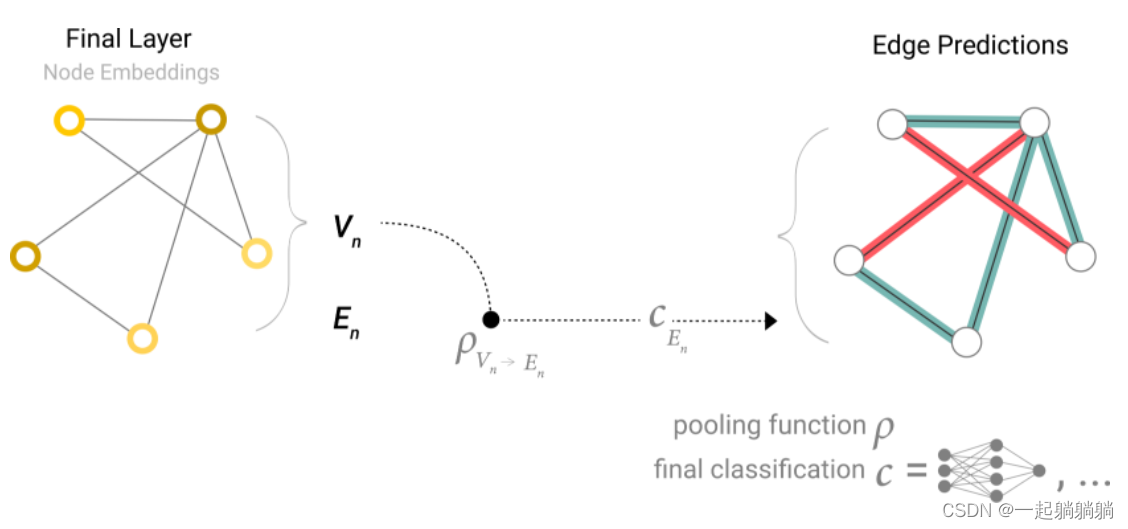
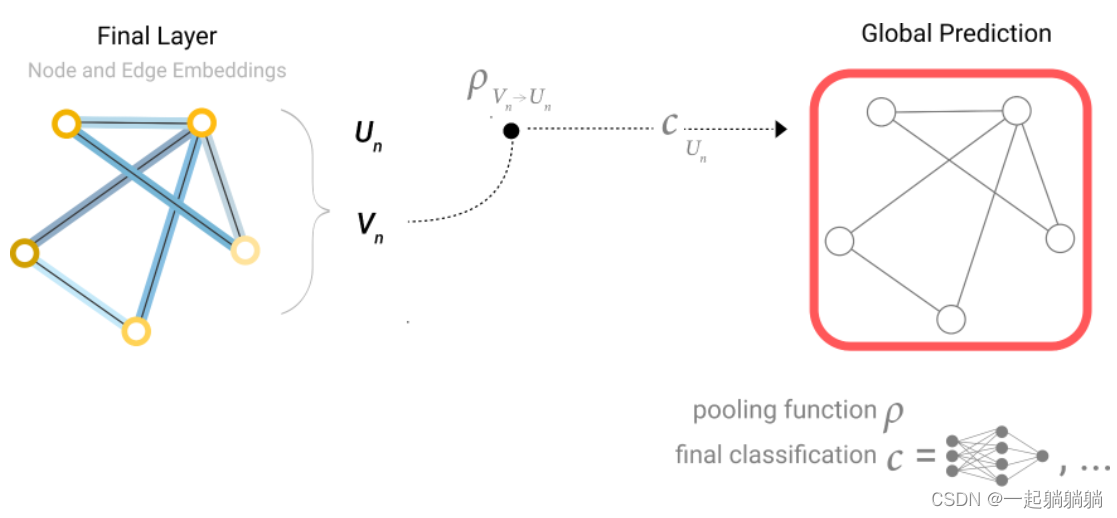
 我们可以将最简单的GNN模型总结成如下的结构。

一张图输入，经过GNN层（5.2讲的那个，实质上就是三个分别对应点、边和全局的MLP），输出一个属性已经变换但是连接性不变的图，在经过全连接层，得到输出。

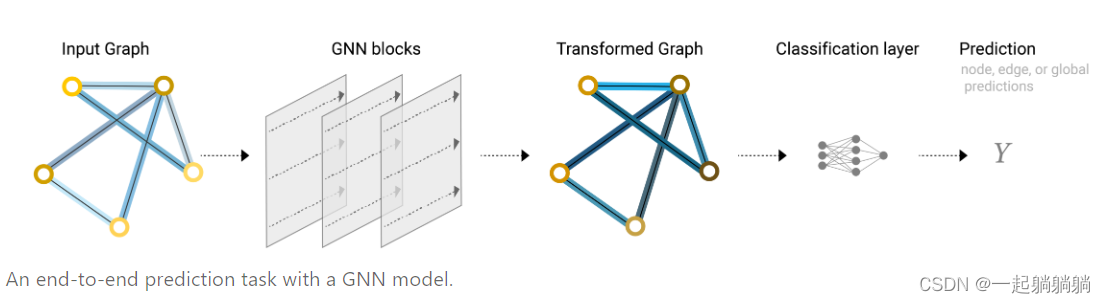
这个结构中，我们没有利用到图各部分之间的连接性，每个部分都是单独处理的，仅仅在池化的时候用了其他部分的信息，下面将告诉大家，怎么来汇集全图信息。

5.4 Passing messages between parts of the graph

我们可以在GNN层中使用池化来感知到图形的连通性，做出更复杂的预测。可以通过passing messages来完成，通过消息传递，相邻节点或边缘传递信息并影响彼此的更新。

消息传递分为三步：

a. 对于图中的每个节点，收集所有相邻节点嵌入(或消息)。

b. 通过聚合函数(如sum)聚合所有消息。

c. 所有合并的消息都通过一个更新函数传递，通常是一个学习过的神经网络。

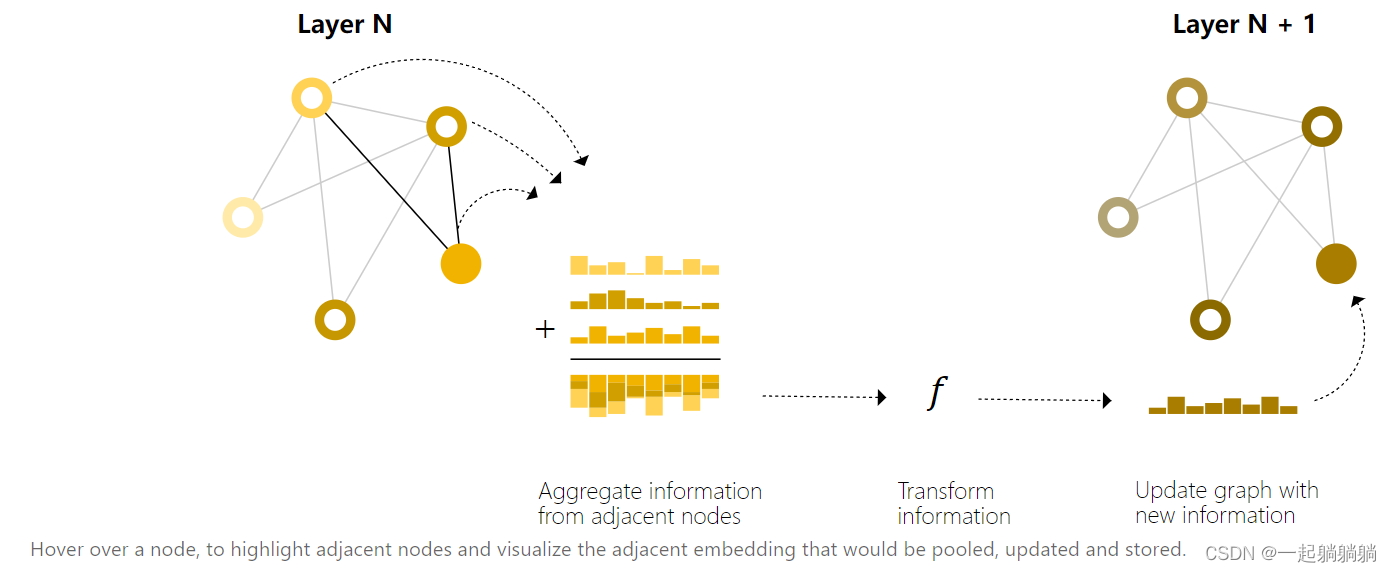
 消息传递可以在顶点或边之间发生，这是我们利用图形连结性的关键，我们将在GNN层中构建更详细的消息传递变体，以产生具有增强表现力和力量的GNN模型。

这让人想起标准卷积：本质上，消息传递和卷积是聚合和处理元素邻居信息以更新元素值的操作。在图形中，元素是一个节点，在图像中，元素是一个像素。但是，图形中相邻节点的数量可以是可变的，这与图像中每个像素具有固定数量的相邻元素不同。

通过将消息传递GNN层堆叠在一起，节点最终可以合并来自整个图的信息：在三层之后，节点具有距离它三步之遥的节点的信息。

我们可以更新我们的架构图，以包含节点的这个新信息源：

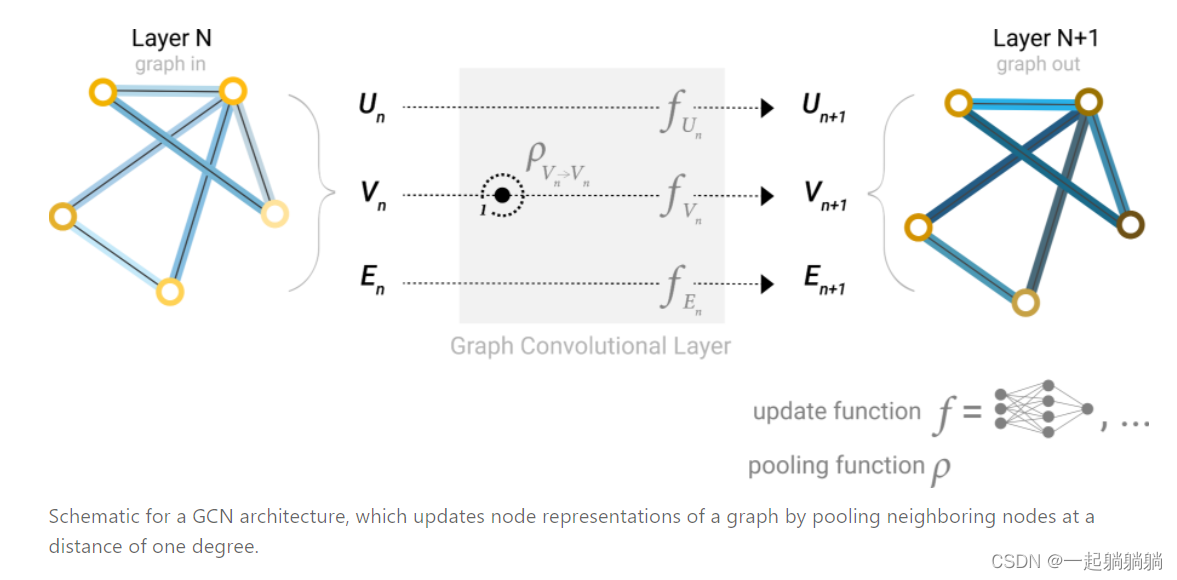
下面这个符号，表示的是聚合该顶点1近邻的顶点信息，就是聚合距离该顶点为1的顶点信息。

5.5 Learning edge representations

我们在上文介绍了如何使用池化将边的信息用来做顶点的预测，但是这一步仅仅在最后的预测步骤中。我们可以使用消息传递，在GNN层内进行顶点和边的信息共享。

就是先把与边连接的顶点信息池化，传递到边上，边通过更新后，再把与顶点相连接的边信息池化传递给顶点，再通过MLP进行更新。如果顶点和边向量的长度不一样，需要先通过投影到相同维度，在做传递。

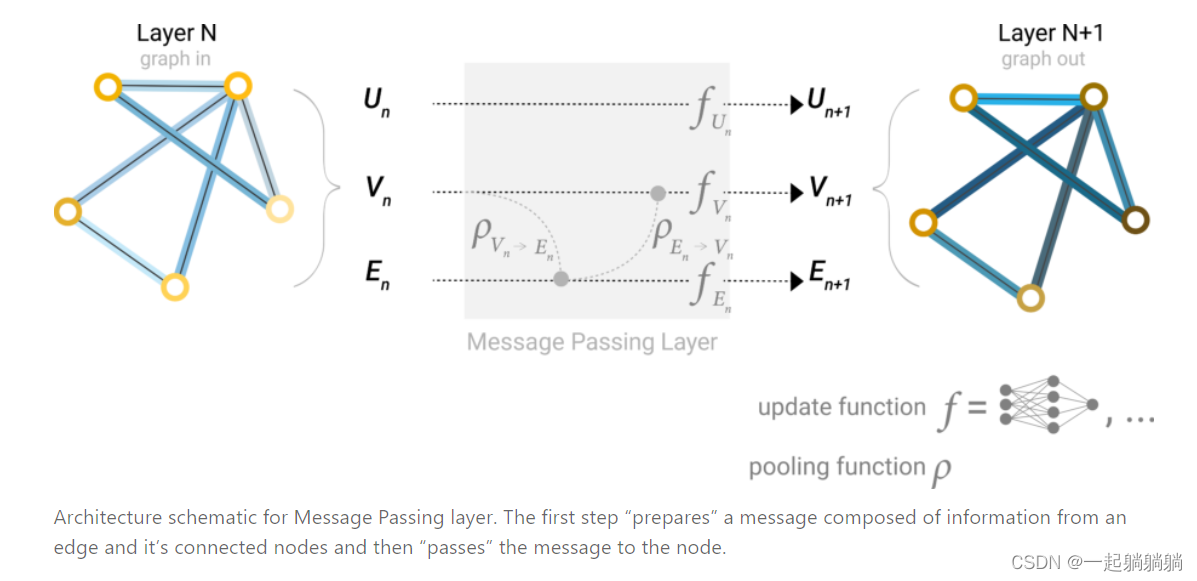
而且是边传给节点还是节点传递给边是由我们来决定的，这会导致不一样的结果，但是目前并没有明确的研究表明，哪种方式更好。但是我们可以将这两种方法同时使用，就是先将顶点信息汇聚给边，同时将边信息汇聚给顶点，然后更新顶点和边，更新后再将边信息传递给顶点，同时将顶点信息传递给边，再通过MLP进行更新

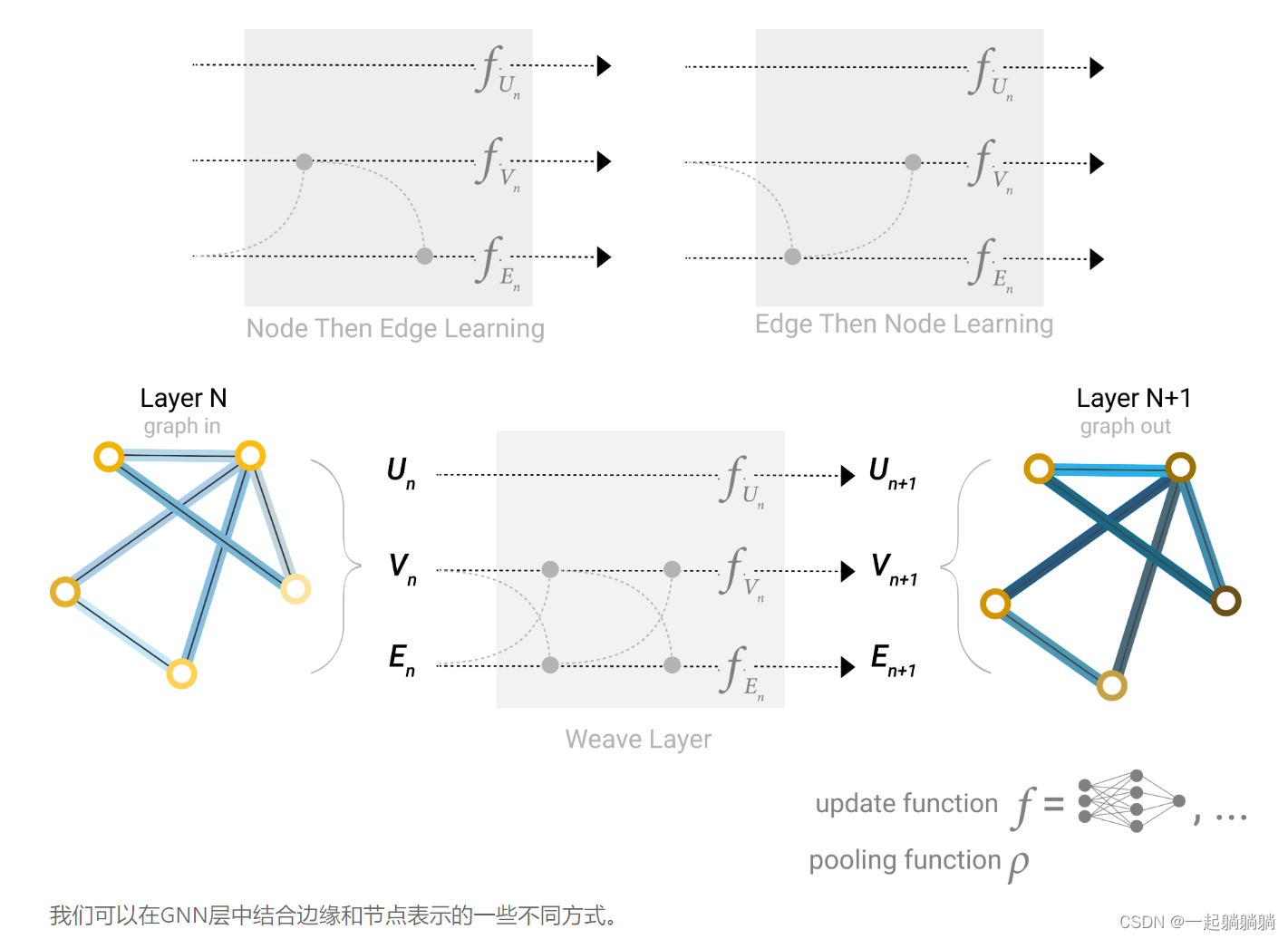
5.6 加入全局信息

我们之前的消息传递，只考虑了1近邻的点，如果一个点想要了解到距离他很远的信息，这是一个问题。为此我们提出master node or context vector，这是一个虚拟的点，他可以和任何其他点或者任何边相连接，这个就是全局信息U。 U是全局信息，它可以和图中的任何信息相连接。

在汇聚顶点信息到边的时候，也会把U一起汇聚，把边信息传递给顶点的时候，也会把U一起传递；然后更新边和顶点后，将边和顶点的信息一起汇聚给U，之后做MLP更新。

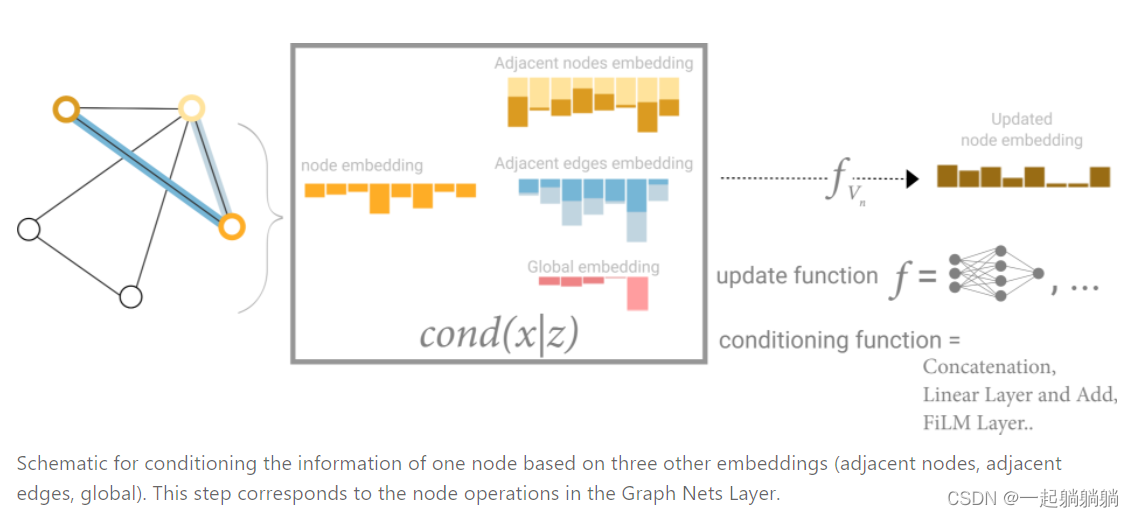
In this view all graph attributes have learned representations, so we can leverage them during pooling by conditioning the information of our attribute of interest with respect to the rest. For example, for one node we can consider information from neighboring nodes, connected edges and the global information. To condition the new node embedding on all these possible sources of information, we can simply concatenate them. Additionally we may also map them to the same space via a linear map and add them or apply a feature-wise modulation layer[22], which can be considered a type of featurize-wise attention mechanism.（原文）

意思就是，在顶点预测中，我们可以用顶点信息、相邻顶点信息、连接边信息、全局信息中的全部或者选择其中几项，来更新顶点信息，做顶点预测；这些信息可以简单地加在一起，也可以通过其他方式汇聚在一起。

六、 GNN playground

原博客中，作者搭建了一个具有小分子图的图级预测任务模型，作者将一个GNN的预测程序嵌入到了java script里面，读者可以自行调节一些超参数来看预测结果，强烈建议自己去原博客看一看（链接：A Gentle Introduction to Graph Neural Networks）（如果加载不了请科学上网）。

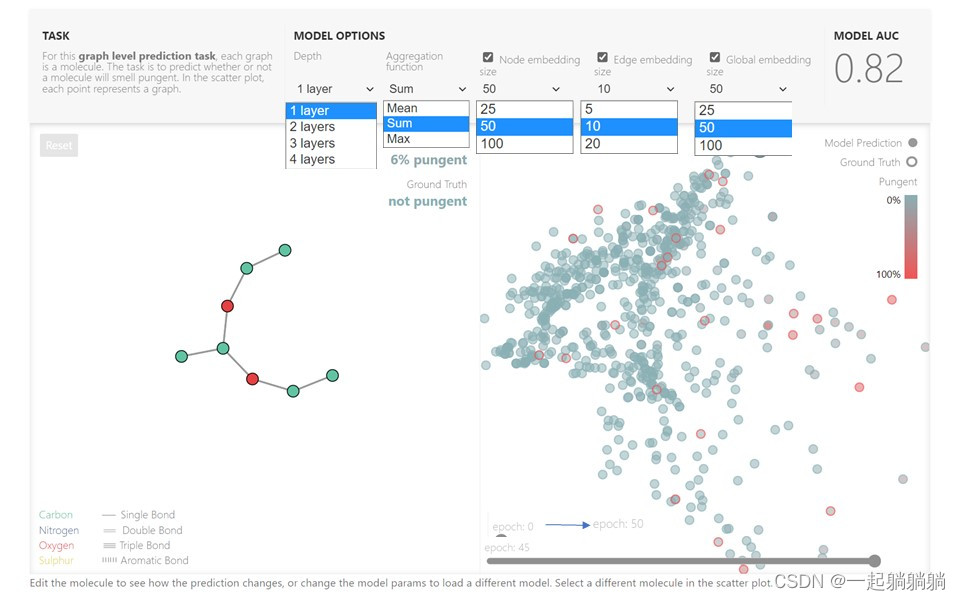
 图中的都是可以改变的超参，可以直接在浏览器里面运行，不需要额外安装任何插件什么的。

Node embedding、Edge embedding、Global embedding这三个还可以选择是否使用，并且左边的分子图是可以改变的，作者牛皮！！！

 6.1 一些GNN的设计经验

在探索上述体系结构选择时，您可能已经发现某些模型的性能优于其他模型。有没有一些明确的GNN设计选择可以给我们带来更好的性能？例如，较深的GNN模型是否比较浅的GNN模型表现更好？还是在聚合函数之间有明确的选择？答案将取决于数据，甚至不同的特征化和构造图的方式也可以给出不同的答案。[25][26]

通过下面的交互式图，我们探索了GNN架构的空间以及该任务在几个主要设计选择中的性能：消息传递的样式，嵌入的维度，层数和聚合操作类型。

散点图中的每个点都表示一个模型：x 轴是可训练变量的数量，y 轴是性能。将鼠标悬停在某个点上可查看 GNN 架构参数。

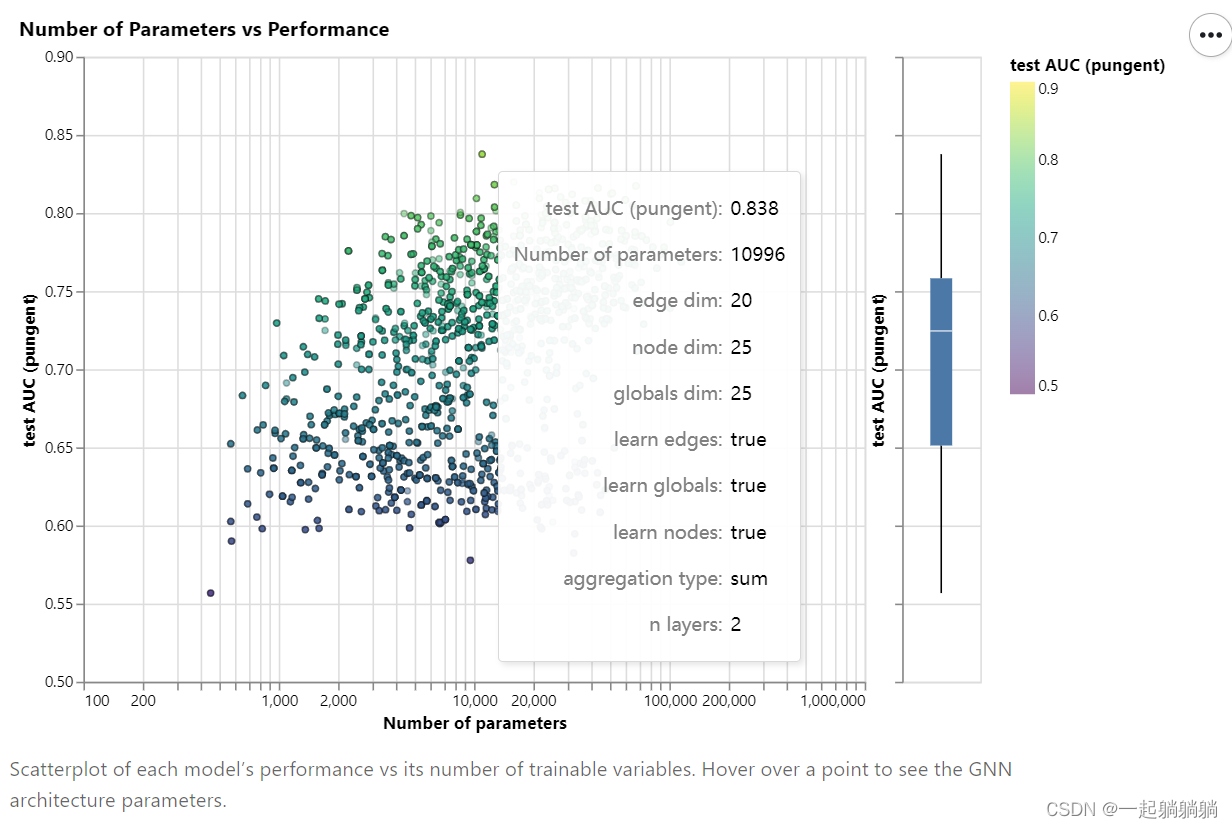
 而且点击右上角有惊喜：

从图中可以看出随着参数数量的增加，模型AUG的上限是在提高的，但是有一个度。

接下来我们看每个参数对模型结果的影响。

6.1.1 顶点、边和全局信息的向量长度

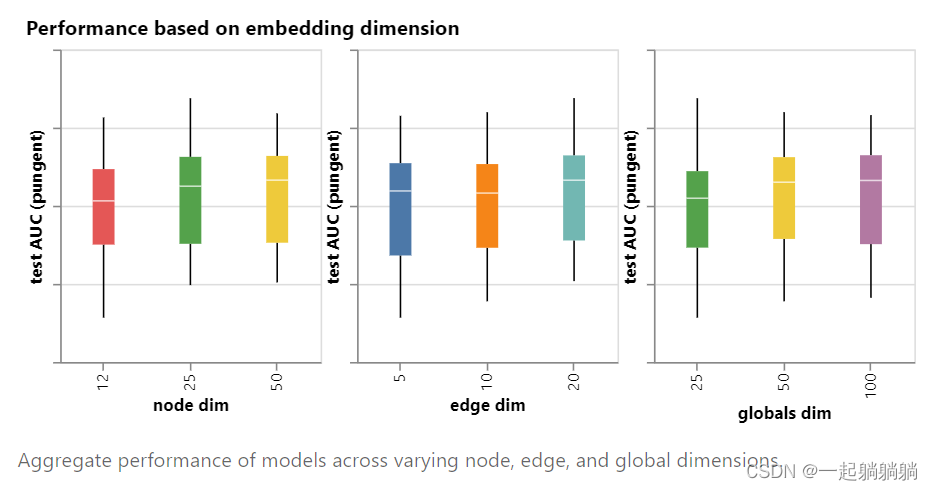
 每一种信息有三个对比，每一个对比都是通过固定向量长度，改变其他参数来得到的结果。图中柱体中的白线指的是中值，白线上下的柱体分别表示比种植高或者低25%的结果；当然希望那条白线越高越好，柱体整体不要太长，越长就表示结果跨度越大，越不稳定。

我们可以注意到，具有较高维数的模型往往具有更好的均值和下限性能，但对于最大值却找不到相同的趋势。

6.1.2 GNN的层数

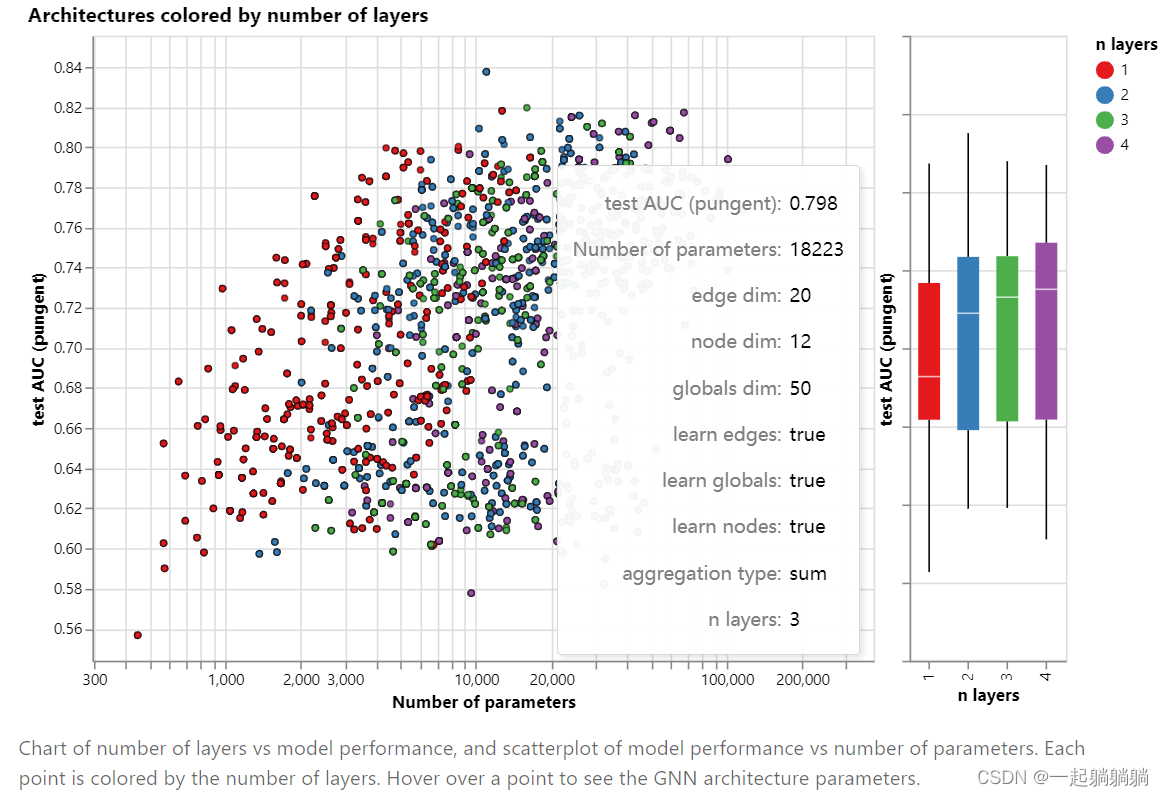
箱形图显示出类似的趋势，虽然平均性能往往随着层数的增加而增加，但性能最佳的模型不是三层或四层，而是两层。此外，性能的下限随着四层的降低而降低。以前已经观察到这种效应，具有较高层数的GNN将在更高的距离广播信息，并且可能冒着从许多连续迭代中“稀释”其节点信息的风险。[27]

6.1.3 聚合函数

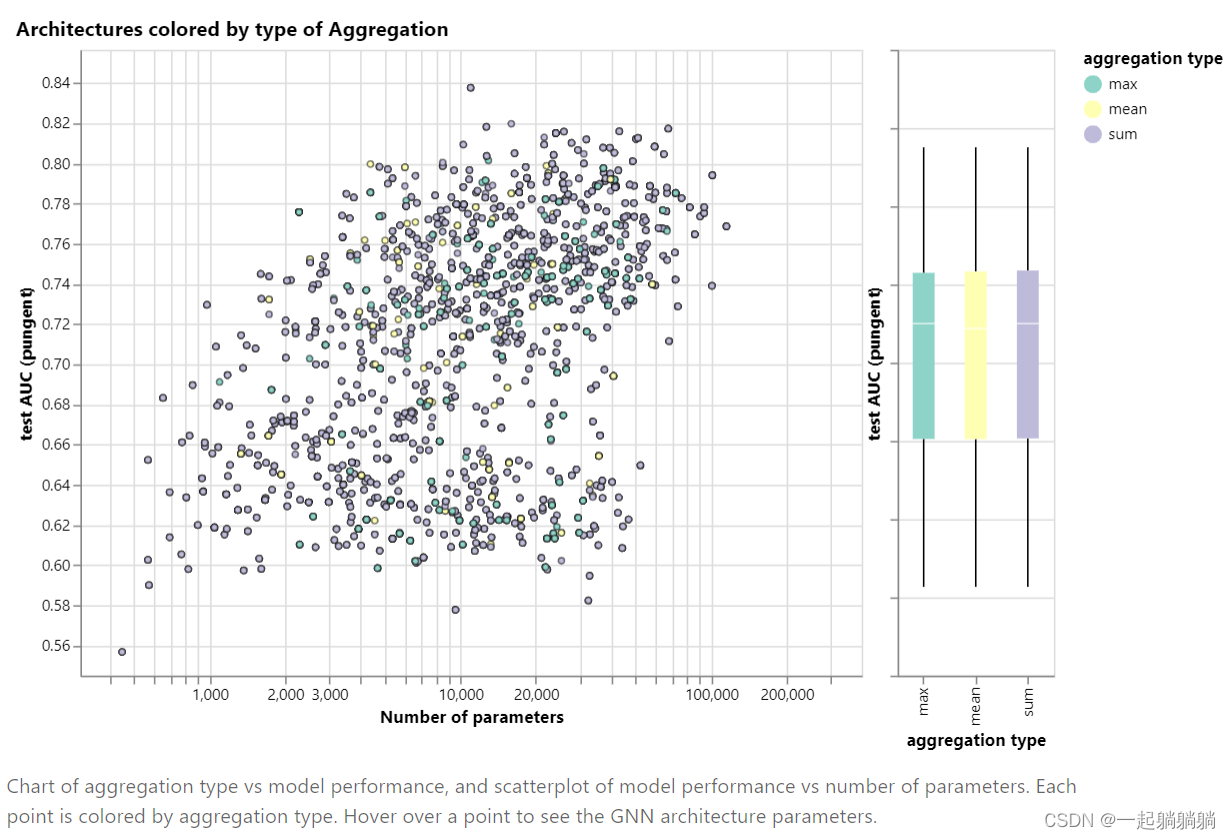
 总体上看，三种聚合函数都差别不大。

6.1.4 信息传递

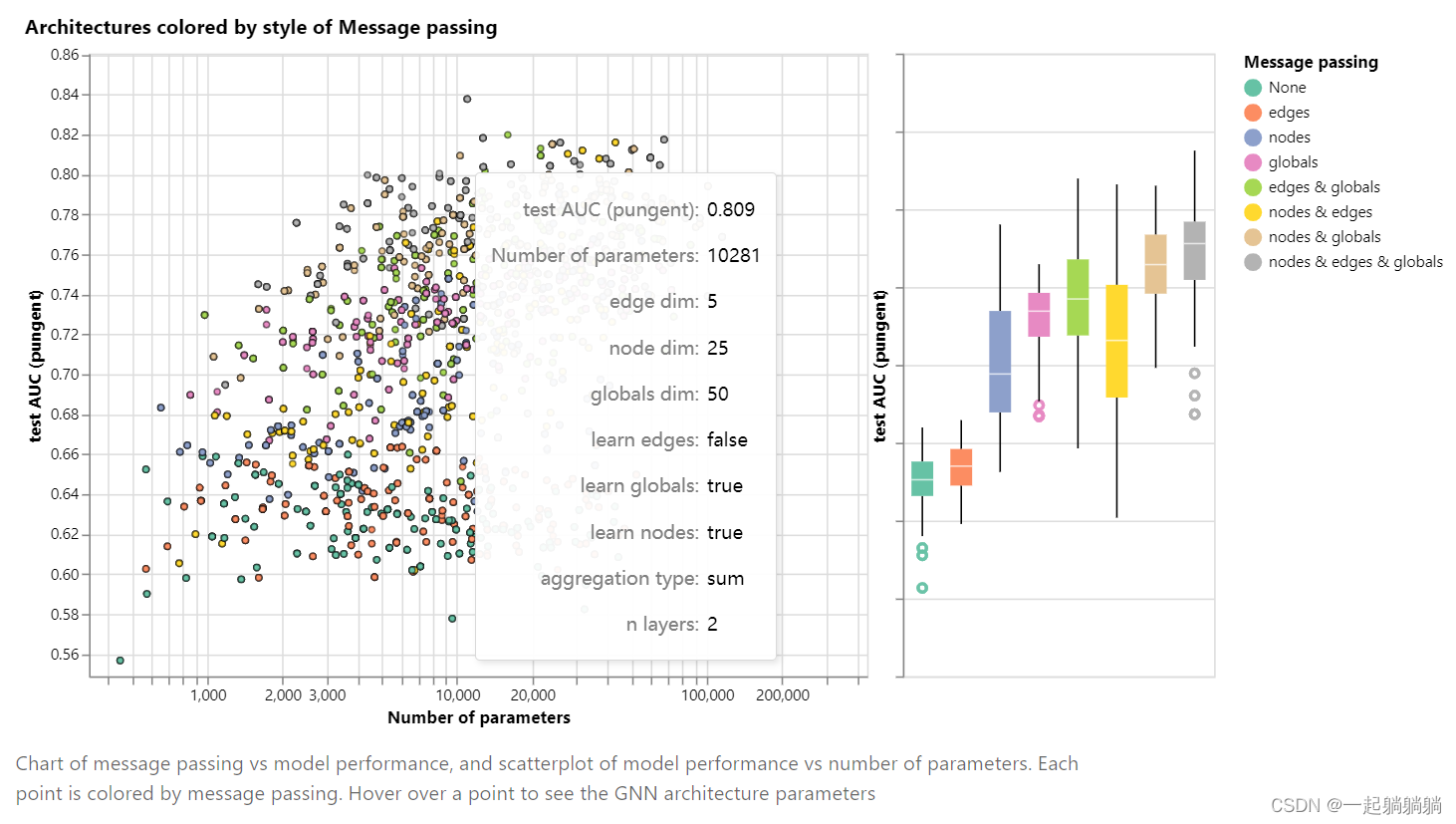
 总体而言，我们看到图形属性传达的越多，平均模型的性能就越好。我们的任务以全局表示为中心，因此明确学习此属性也有助于提高性能。我们的节点表示似乎也比边缘表示更有用，这是有道理的，因为这些信息加载在这些属性中。

七、 GNN相关的技术

7.1 其他类型的图

上面我们只考虑了单边图，现实中信息的内容是多样的，比如社会关系交错臃杂，不是单边图能够描绘清楚的，我们可以考虑很多种其他类型的图。比如，对于社交网络，我们可以根据关系类型（熟人，朋友，家人）指定边缘类型。可以通过为每个边缘类型提供不同类型的消息传递步骤来调整 GNN。我们还可以考虑嵌套图，例如节点表示图，也称为超节点图。嵌套图形对于表示分层信息非常有用。例如，我们可以考虑一个分子网络，其中一个节点代表一个分子，如果我们有将一个分子转换为另一个分子的方法（反应），则两个分子之间共享一个边缘。在这种情况下，我们可以通过有一个GNN在分子水平上学习表示，另一个在反应网络水平上学习表示，并在训练期间交替使用它们。[32][33][34][35]

另一种类型的图形是超图，其中一条边可以连接到多个节点，而不仅仅是两个节点。对于给定的图形，我们可以通过识别节点社区并分配连接到社区中所有节点的超边缘来构建超图。[36]

 如上图所示，边的类型有三种，红色和蓝色的无向边，绿色的有向边；以及右图，图是分层的，其中的一些节点是一个子图，就是hypernodes。

不同图的结构会在神经网络做汇聚的时候产生不同的影响，需要根据图的结构实时调整。

7.2 GNN中的采样和bath

如果GNN有很多层，就算每一次只做1近邻，到最后一层中的一个节点可能包含有整个图的信息。在神经网络中计算梯度的时候，我们需要将整个梯度给保存下来，如果对最后一个顶点计算梯度的时候，我们需要保存整个图的中间结果，如果图很大，这可能会导致我们是无法承受的。所以我们也需要做小批量梯度，就是每次从图中随机采集一个小图，然后在这个小图上面做汇聚，计算梯度的时候只需要保存小图上面的结果就足够了。

下面介绍几种采样的方法。

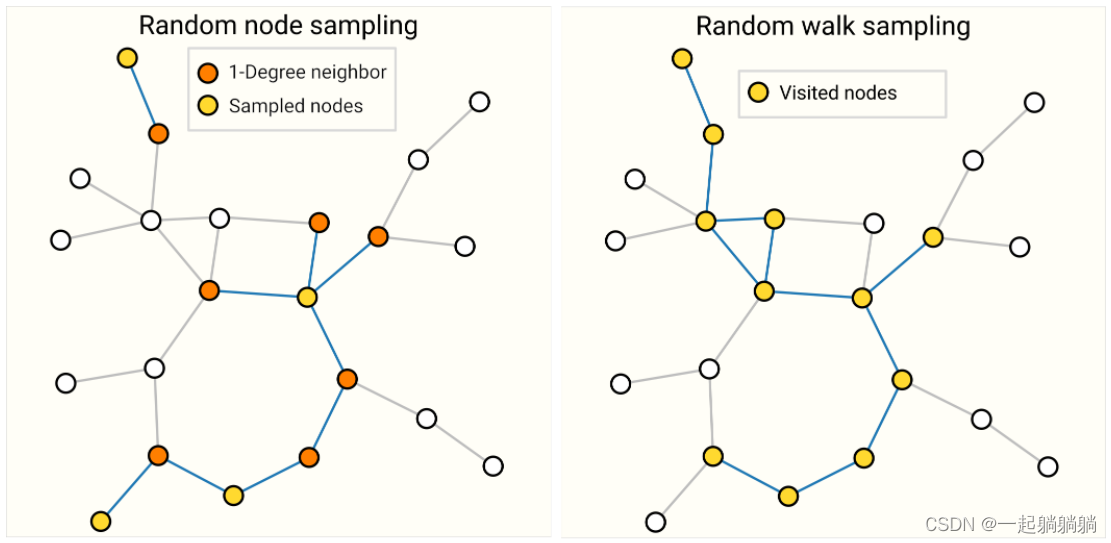
 上图中，左边是说随机采样一些点，然后把这些点的1近邻找出来，构成子图，做计算的时候只在子图上做计算，我们可以控制这个子图的大小；右图是通过随机游走，随机找到一个点，从这个点开始随机游走，规定走多少步，然后得到一个子图。

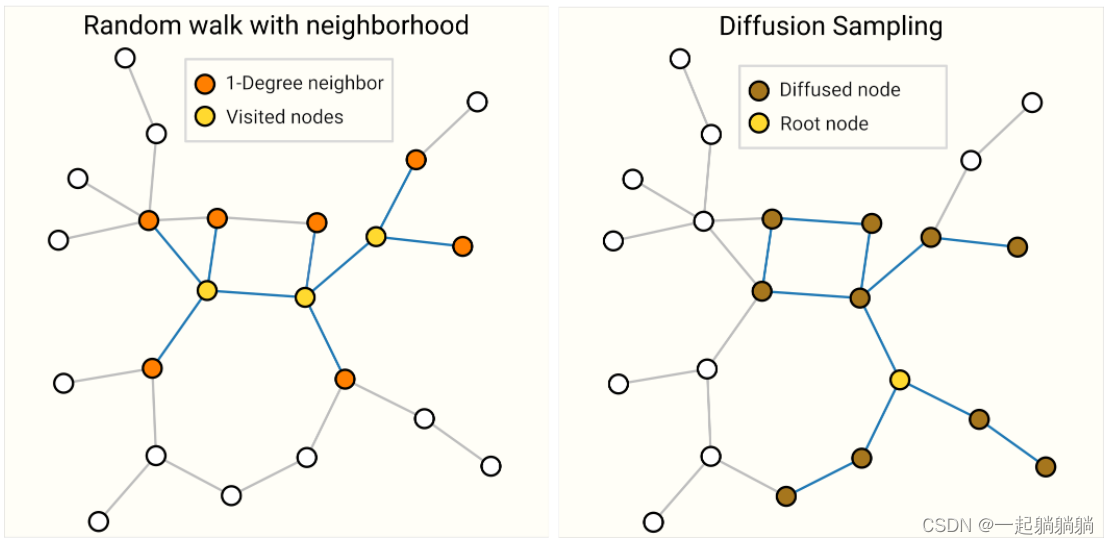
 这个图中的左图，是结合上面两种方法，我先随机游走三步，然后找出这些点的1近邻，构成一个子图；右图是随机取一个点，然后把这个点的k近邻找出来构成一个子图。

这是四种不同的采样方法，不同的图适合不同的采样方法。下面的一个问题是做bath。

从性能上考虑，我们不想对每一个顶点逐步更新，这样每一步的计算量太小，不利于并行，我们希望像别的网络一样，我们能把这个小样本做成小批量，这样我们就能对一个大的矩阵做运算，这里有一问题就是，每一个顶点的邻居数量可能是不同的，怎样把这些顶点的邻居合并并成一个规则的张量，这是一个有挑战的问题。

7.3 Inductive biases

就是对于任何一个模型，不管是神经网络也好，传统机器学习也好，都有一些假设前提，如果没有这些假设，这些模型是不成立的。

比如，CNN假设的是空间变换的不变性，RNN假设的是时序的延续性，那对GNN的假设是什么呢？

GNN的假设就是前面说到的两大特点之一，图的对称性；就是说不管你如何改变图中顶点的顺序，GNN对齐的作用都是保持不变的。

7.4 不同汇聚操作的比较

前面说到过，汇聚操作可以求和、求平均、求最大值等，但是没有一种是理想的。聚合操作的一个理想属性是，相似的输入提供相似的聚合输出，反之亦然。

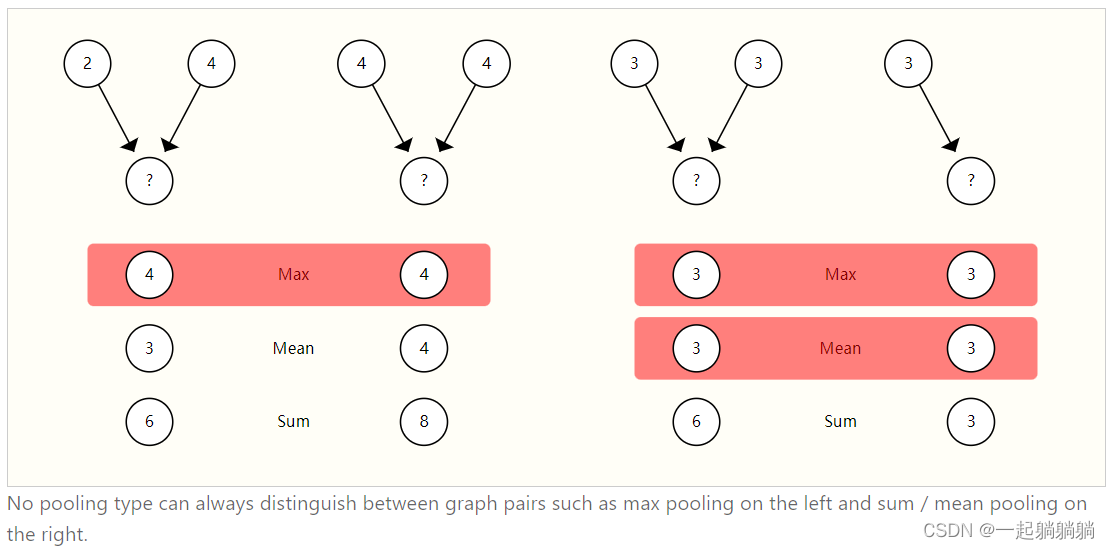
上面左图中，两个点对做汇聚，用三种不同汇聚操作得到不同的结果，其中max得到的结果是一样的，但是点对并不一样；右图中两个点对，max和mean得到的结果也是一样的，但是点对并不相同；sum也很容易找到无法区分点对的例子，比如点对分别为1、5和4、2，这个例子中sum得到的结果也是一样的。没有一种是更好的，需要具体问题分别对待，但是更多的是选择求和。

7.4 GCN作为子图的函数近似

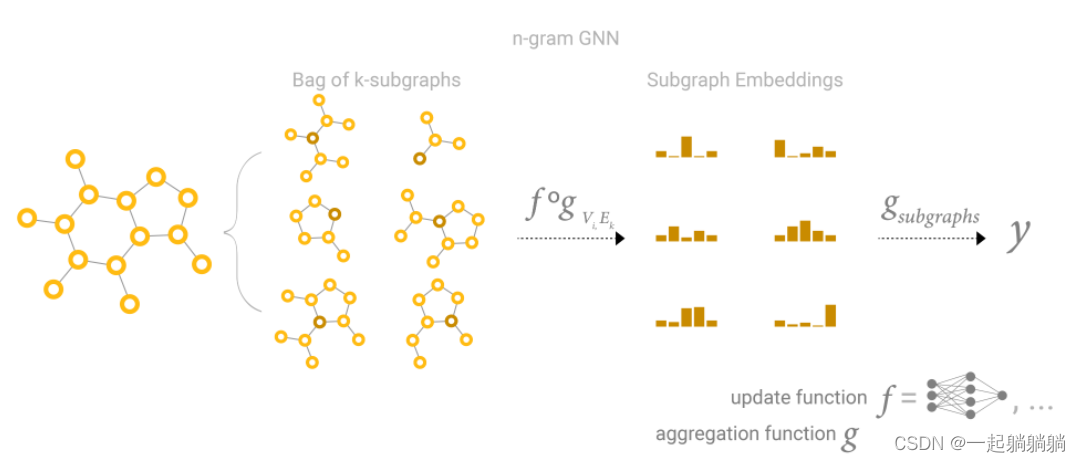
博客上文中并没有提及GCN，GCN是图卷积神经网络，就是我们前面提到的那个代理汇聚操作的图神经网络。GCN如果有k个层，每一层都做1近邻，（这个类似于CNN中我们有K层3*3的卷积），那么到最后，就相当于每一个顶点看到的是一个子图，子图最远点到该顶点的距离为k。

所以可以说是每个顶点做K近邻顶点的信息汇聚，从一定程度上来说，GCN就可以认为是有n个k大小的子图，然后对这些子图求一个embedding出来。

......后面内容就不写了，博客有点草草结束的意思，又想去可以自己看看。