- 1新能源安全之路:温度芯片助力充电桩实现智能温度监控
- 2机器学习之决策树-python实现_决策树operator
- 3软考 - 系统架构设计师 - 数据管理能力成熟度评估模型(DCMM)_dcmm 软考
- 4软考高项—第一章信息系统项目管理基础_软考高项 第一章csdn
- 5vue 部署
- 6Pip使用中遇到的问题:Fatal error in launcher: Unable to create process using XXX_pip fatal error in launcher: unable to create proc
- 7【接口测试】工具篇Postman_在线postman
- 8pyltp实体识别_哈工大 PYLTP 安装 排坑指南
- 9山东大学机器人实验 ROS 总结
- 10jdk8和17无缝切换,安装idea且免费使用,maven安装配置一条龙超详细!(保姆教程)_idea 安装 jdk17
2021秋招-算法-BFS-DFS_秋招算法 dfs-bfs
赞
踩
LeetCode刷题总结-DFS、BFS和回溯法篇

一、深度优先搜索
一、字符匹配问题
[1.lc-301. 删除无效的括号-困难]
二、数组或字符串问题
[1. lc-329. 矩阵中的最长递增路径-困难]
[2. lc-488. 祖玛游戏-困难]
[3. lc-491. 递增子序列-中等]
三、特定场景应用问题
[1. lc-679. 24 点游戏-困难]
[2. lc-1254. 统计封闭岛屿的数目-中等]
二、广度优先搜索
一、数组或字符串问题
[1. lc-127. 单词接龙-中等]
[2. lc-1091. 二进制矩阵中的最短路径-中等]
二、特定场景应用问题
[1. lc-773. 滑动谜题-困难]
[2. lc-815. 公交路线-困难]
三、回溯法
数组或字符串问题
[1. 题号:47. 全排列 II-中等]
[2. 题号:51. N皇后-困难]
[3. 题号:131. 分割回文串-中等]
BFS-DFS总结

知乎-DFS & BFS(基础基础篇) 提供两种搜索思想伪代码、框架 (⭐⭐⭐)
知乎-LeetCode|一文帮你搞定BFS、DFS算法(python版)⭐⭐⭐
同样总结了模板以及常见的问题类型;
⭐⭐⭐BFS相关题目
一些说明记录:
1. 列表的pop(0)方法复杂度时O(N),不能用来做队列。可以用collections.deque或queue.Queue
1.1 from collections import deque # 导入 deque包
1.2 queue = deque() # 实例化、初始化一个 队列 queue = []
1.3 queue.append((i, j)) # 队列中添加元素
1.4 queue.popleft() # queue.pop(0)
- 1
- 2
- 3
- 4
- 5
模板:
# python def BFS(start, target): queue = [] # 核心数据结构 visited = set() # 避免走回头路 queue.append(start) # 将起点加入队列 visited.add(start) step = 0 # 记录扩散的步数 while queue: # queue_size: 本质作用, 记录一步或者一层 队列中有几个元素; # 如果结果不结算层、不计算多少步, 其实也没必要的; queue_size = len(queue) # 当前step 队列中的元素 # 将当前队列中所有节点向四周扩散 for i in range(queue_size): curNode = queue.pop(0) # 获取当前节点 # 划重点:这里判断是否到达终点 if curNode is target: return step # 将curNode 的相邻节点加入队列 for (Node -x in curNode.adj()): if (x not in visited): queue.append(x) visited.add(x) # 不存在pop(), 故可以保留历史信息 # 划重点: 更新步数在这里 step += 1
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
BFS-大佬写的框架,后面也是搬运此文章 ⭐⭐⭐⭐
BFS 的核心思想应该不难理解的,就是把一些问题抽象成图,从一个点开始,向四周开始扩散。一般来说,我们写 BFS 算法都是用「队列」这种数据结构,每次将一个节点周围的所有节点加入队列。
BFS 相对 DFS 的最主要的区别是:BFS 找到的路径一定是最短的,但代价就是空间复杂度比 DFS 大很多,至于为什么,我们后面介绍了框架就很容易看出来了。
本文就由浅入深写两道 BFS 的典型题目,分别是「二叉树的最小高度」和「打开密码锁的最少步数」,手把手教你怎么写 BFS 算法。
一、BFS-算法框架
要说框架的话,我们先举例一下 BFS 出现的常见场景好吧,问题的本质就是让你在一幅「图」中找到从起点start到终点target的最近距离,这个例子听起来很枯燥,但是 BFS 算法问题其实都是在干这个事儿。
把枯燥的本质搞清楚了,再去欣赏各种问题的包装才能胸有成竹嘛。
这个广义的描述可以有各种变体,比如走迷宫,有的格子是围墙不能走,从起点到终点的最短距离是多少?如果这个迷宫带「传送门」可以瞬间传送呢?
再比如说两个单词,要求你通过某些替换,把其中一个变成另一个,每次只能替换一个字符,最少要替换几次?
再比如说连连看游戏,两个方块消除的条件不仅仅是图案相同,还得保证两个方块之间的最短连线不能多于两个拐点。你玩连连看,点击两个坐标,游戏是如何判断它俩的最短连线有几个拐点的?
再比如……
净整些花里胡哨的,这些问题都没啥奇技淫巧,本质上就是一幅「图」,让你从一个起点,走到终点,问最短路径。这就是 BFS 的本质,框架搞清楚了直接默写就好。

记住下面这个框架就 OK 了:
// 计算从起点 start 到终点 target 的最近距离 int BFS(Node start, Node target) { Queue<Node> q; // 核心数据结构 Set<Node> visited; // 避免走回头路 q.offer(start); // 将起点加入队列 visited.add(start); int step = 0; // 记录扩散的步数 while (q not empty) { int sz = q.size(); /* 将当前队列中的所有节点向四周扩散 */ for (int i = 0; i < sz; i++) { Node cur = q.poll(); /* 划重点:这里判断是否到达终点 */ if (cur is target) return step; /* 将 cur 的相邻节点加入队列 */ for (Node x : cur.adj()) if (x not in visited) { q.offer(x); visited.add(x); } } /* 划重点:更新步数在这里 */ step++; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
# python def BFS(start, target): queue = [] # 核心数据结构 visited = set() # 避免走回头路 queue.append(start) # 将起点加入队列 visited.add(start) step = 0 # 记录扩散的步数 while queue: queue_size = len(queue) # 当前step 队列中的元素 # 将当前队列中所有节点向四周扩散 for i in range(queue_size): curNode = queue.pop(0) # 获取当前节点 # 划重点:这里判断是否到达终点 if curNode is target: return step # 将curNode 的相邻节点加入队列 for (Node -x in curNode.adj()): if (x not in visited): queue.append(x) visited.add(x) # 不存在pop(), 故可以保留历史信息 # 划重点: 更新步数在这里 step += 1
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
队列q就不说了,BFS 的核心数据结构;cur.adj()泛指cur相邻的节点,比如说二维数组中,cur上下左右四面的位置就是相邻节点;visited的主要作用是防止走回头路,大部分时候都是必须的,但是像一般的二叉树结构,没有子节点到父节点的指针,不会走回头路就不需要visited。
二、二叉树的最小高度:leetcode-111-简单
LeetCode链接

怎么套到 BFS 的框架里呢?首先明确一下起点start和终点target是什么,怎么判断到达了终点?
显然起点就是root根节点,终点就是最靠近根节点的那个「叶子节点」嘛,叶子节点就是两个子节点都是null的节点:
if not curNode.left and not curNode.right:
# 达到叶子节点
- 1
- 2
那么,按照我们上述的框架稍加改造来写解法即可:
int minDepth(TreeNode root) { if (root == null) return 0; Queue<TreeNode> q = new LinkedList<>(); q.offer(root); // root 本身就是一层,depth 初始化为 1 int depth = 1; while (!q.isEmpty()) { int sz = q.size(); /* 将当前队列中的所有节点向四周扩散 */ for (int i = 0; i < sz; i++) { TreeNode cur = q.poll(); /* 判断是否到达终点 */ if (cur.left == null && cur.right == null) return depth; /* 将 cur 的相邻节点加入队列 */ if (cur.left != null) q.offer(cur.left); if (cur.right != null) q.offer(cur.right); } /* 这里增加步数 */ depth++; } return depth; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
python提交代码
# python - # Definition for a binary tree node. # class TreeNode: # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution: def minDepth(self, root: TreeNode) -> int: # BFS: 时间复杂度相对DFS较低, 但是空间复杂度O(N) > DFS:O(log N) if not root: return 0 queue = [root] # BFS使用队列 depth = 1 # 初始化高度/深度 while queue: # 记录队列中元素数量: 二叉树每一层node数量 queue_size = len(queue) # 遍历二叉树一层node, 并将周围节点加入 队列 for i in range(queue_size): # 取最先进入队列元素 curNode = queue.pop(0) # 判断是否到达终点 if not curNode.left and not curNode.right: return depth # 将当前节点周围node加入队列 if curNode.left: queue.append(curNode.left) if curNode.right: queue.append(curNode.right) # 遍历一层, 深度 +1 depth += 1
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
二叉树是很简单的数据结构,我想上述代码你应该可以理解的吧,其实其他复杂问题都是这个框架的变形,在探讨复杂问题之前,我们解答两个问题:
1、为什么 BFS 可以找到最短距离,DFS 不行吗?
首先,你看 BFS 的逻辑,depth每增加一次,队列中的所有节点都向前迈一步,这保证了第一次到达终点的时候,走的步数是最少的。
DFS 不能找最短路径吗?其实也是可以的,但是时间复杂度相对高很多。
你想啊,DFS 实际上是靠递归的堆栈记录走过的路径,你要找到最短路径,肯定得把二叉树中所有树杈都探索完才能对比出最短的路径有多长对不对?
而 BFS 借助队列做到一次一步「齐头并进」,是可以在不遍历完整棵树的条件下找到最短距离的。
形象点说,DFS 是线,BFS 是面;DFS 是单打独斗,BFS 是集体行动。这个应该比较容易理解吧。
2、既然 BFS 那么好,为啥 DFS 还要存在?
BFS 可以找到最短距离,但是空间复杂度高,而 DFS 的空间复杂度较低。
还是拿刚才我们处理二叉树问题的例子,假设给你的这个二叉树是满二叉树,节点总数为N,对于 DFS 算法来说,空间复杂度无非就是递归堆栈,最坏情况下顶多就是树的高度,也就是O(logN)。
但是你想想 BFS 算法,队列中每次都会储存着二叉树一层的节点,这样的话最坏情况下空间复杂度应该是树的最底层节点的数量,也就是N/2,用 Big O 表示的话也就是O(N)。
由此观之,BFS 还是有代价的,一般来说在找最短路径的时候使用 BFS,其他时候还是 DFS 使用得多一些**(主要是递归代码好写)**。
好了,现在你对 BFS 了解得足够多了,下面来一道难一点的题目,深化一下框架的理解吧。
三、解开密码锁的最少次数-752-中等
LeetCode链接

题目中描述的就是我们生活中常见的那种密码锁,若果没有任何约束,最少的拨动次数很好算,就像我们平时开密码锁那样直奔密码拨就行了。
但现在的难点就在于,不能出现deadends,应该如何计算出最少的转动次数呢?
第一步,我们不管所有的限制条件,不管deadends和target的限制,就思考一个问题:如果让你设计一个算法,穷举所有可能的密码组合,你怎么做?
穷举呗,再简单一点,如果你只转一下锁,有几种可能?总共有 4 个位置,每个位置可以向上转,也可以向下转,也就是有 8 种可能对吧。
比如说从"0000"开始,转一次,可以穷举出"1000", “9000”, “0100”, “0900”…共 8 种密码。然后,再以这 8 种密码作为基础,对每个密码再转一下,穷举出所有可能…
仔细想想,这就可以抽象成一幅图,每个节点有 8 个相邻的节点,又让你求最短距离,这不就是典型的 BFS 嘛,框架就可以派上用场了,先写出一个「简陋」的 BFS 框架代码再说别的:
# python版本 # s[j]向上拨动一次 def plusOne(s, j): # s: [] j:位置j if s[j] == 9: s[j] = 0 else: s[j] += 1 return s # s[i] 向下拨动一次 def minusOne(s, j): if s[j] == 0: s[j] = 9 else: s[j] -= 1 return s # BFS框架 def BFS(start, target): queue = [[0, 0 , 0, 0]] while queue: queue_size = len(queue) # 将当前节点向周围扩散 for i in range(queue_size): curNode = queue.pop(0) # 判断当前是否到达终点:第一次到达就返回, 就是最短路径? if curNode == target: return steps # 将一个节点的相邻节点加入队列: 4位依次遍历 for j in range(4): up = plusOne(curNode, j) down = minusOne(curNode, j) queue.appen(up) queue.append(down) steps += 1 return steps
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
PS:这段代码当然有很多问题,但是我们做算法题肯定不是一蹴而就的,而是从简陋到完美的。不要完美主义,咱要慢慢来,好不。
这段 BFS 代码已经能够穷举所有可能的密码组合,但显然不能完成题目,有如下问题需要解决:
1、会走回头路。比如说我们从"0000"拨到"1000",但是等从队列拿出"1000"时,还会拨出一个"0000",这样的话会产生死循环。
2、没有终止条件,按照题目要求,我们找到target就应该结束并返回拨动的次数。
3、没有对deadends的处理,按道理这些「死亡密码」是不能出现的,也就是说你遇到这些密码的时候需要跳过。
如果你能够看懂上面那段代码,真得给你鼓掌,只要按照 BFS 框架在对应的位置稍作修改即可修复这些问题:
python代码
class Solution: def openLock(self, deadends: List[str], target: str) -> int: # block[j] 向上拨动一次 def plusOne(block, j): block = [int(s) for s in block] if block[j] == 9: block[j] = 0 else: block[j] += 1 return ''.join([str(b) for b in block]) # block[j] 向下拨动一次 def minusOne(block, j): block = [int(s) for s in block] if block[j] == 0: block[j] = 9 else: block[j] -= 1 return ''.join([str(b) for b in block]) # 死亡密码记录 deads = set(deadends) # 记录已经访问过的密码,路径 , 防止走回头路 # 后面添加记得 list--> visited = set(['0000']) # 使用队列,记录当前步数下的密码 queue = ['0000'] # 从起点开始 BFS step = 0 while queue: queue_size = len(queue) # 将当前队列中的节点向周围扩散 for i in range(queue_size): curNode = queue.pop(0) print('-----curNode-----:', curNode) # 判断是否到达终点 if curNode in deads: continue if curNode == target: return step # 将一个节点的未遍历相邻节点加入队列, 8个相邻 for j in range(4): up = plusOne(curNode, j) # 限制不走回头路 if up not in visited: visited.add(up) queue.append(up) print('up_add:', up) down = minusOne(curNode, j) if down not in visited: visited.add(down) queue.append(down) print('down_add:', down) # 步数增加 step += 1 # 遍历完毕,未找到合适路径 return -1
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
至此,我们就解决这道题目了。有一个比较小的优化:可以不需要dead这个哈希集合,可以直接将这些元素初始化到visited集合中,效果是一样的,可能更加优雅一些。
四、双向 BFS 优化
你以为到这里 BFS 算法就结束了?恰恰相反。BFS 算法还有一种稍微高级一点的优化思路:双向 BFS,可以进一步提高算法的效率。
篇幅所限,这里就提一下区别:传统的 BFS 框架就是从起点开始向四周扩散,遇到终点时停止;而双向 BFS 则是从起点和终点同时开始扩散,当两边有交集的时候停止。
为什么这样能够能够提升效率呢?其实从 Big O 表示法分析算法复杂度的话,它俩的最坏复杂度都是O(N),但是实际上双向 BFS 确实会快一些,我给你画两张图看一眼就明白了:


图示中的树形结构,如果终点在最底部,按照传统 BFS 算法的策略,会把整棵树的节点都搜索一遍,最后找到target;而双向 BFS 其实只遍历了半棵树就出现了交集,也就是找到了最短距离。从这个例子可以直观地感受到,双向 BFS 是要比传统 BFS 高效的。
不过,双向 BFS 也有局限,因为你必须知道终点在哪里。比如我们刚才讨论的二叉树最小高度的问题,你一开始根本就不知道终点在哪里,也就无法使用双向 BFS;但是第二个密码锁的问题,是可以使用双向 BFS 算法来提高效率的,代码稍加修改即可:
int openLock(String[] deadends, String target) { Set<String> deads = new HashSet<>(); for (String s : deadends) deads.add(s); // 用集合不用队列,可以快速判断元素是否存在 Set<String> q1 = new HashSet<>(); Set<String> q2 = new HashSet<>(); Set<String> visited = new HashSet<>(); int step = 0; q1.add("0000"); q2.add(target); while (!q1.isEmpty() && !q2.isEmpty()) { // 哈希集合在遍历的过程中不能修改,用 temp 存储扩散结果 Set<String> temp = new HashSet<>(); /* 将 q1 中的所有节点向周围扩散 */ for (String cur : q1) { /* 判断是否到达终点 */ if (deads.contains(cur)) continue; if (q2.contains(cur)) return step; visited.add(cur); /* 将一个节点的未遍历相邻节点加入集合 */ for (int j = 0; j < 4; j++) { String up = plusOne(cur, j); if (!visited.contains(up)) temp.add(up); String down = minusOne(cur, j); if (!visited.contains(down)) temp.add(down); } } /* 在这里增加步数 */ step++; // temp 相当于 q1 // 这里交换 q1 q2,下一轮 while 就是扩散 q2 q1 = q2; q2 = temp; } return -1; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
双向 BFS 还是遵循 BFS 算法框架的,只是不再使用队列,而是使用 HashSet 方便快速判断两个集合是否有交集。
另外的一个技巧点就是 while 循环的最后交换q1和q2的内容,所以只要默认扩散q1就相当于轮流扩散q1和q2。
其实双向 BFS 还有一个优化,就是在 while 循环开始时做一个判断:
// ...
while (!q1.isEmpty() && !q2.isEmpty()) {
if (q1.size() > q2.size()) {
// 交换 q1 和 q2
temp = q1;
q1 = q2;
q2 = temp;
}
// ...
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
为什么这是一个优化呢?
因为按照 BFS 的逻辑,队列(集合)中的元素越多,扩散之后新的队列(集合)中的元素就越多;在双向 BFS 算法中,如果我们每次都选择一个较小的集合进行扩散,那么占用的空间增长速度就会慢一些,效率就会高一些。
不过话说回来,无论传统 BFS 还是双向 BFS,无论做不做优化,从 Big O 衡量标准来看,空间复杂度都是一样的,只能说双向 BFS 是一种 trick 吧,掌握不掌握其实都无所谓。最关键的是把 BFS 通用框架记下来,反正所有 BFS 算法都可以用它套出解法。
111-二叉树的最小高度-简单

- python实现
class Solution:
def minDepth(self, root: TreeNode) -> int:
# 思路1: 层次遍历
if not root:
return 0
left = self.minDepth(root.left)
right = self.minDepth(root.right)
if root.left and root.right:
return min(left, right) + 1
else:
return 1 + left + right
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
752-解开密码锁的最小次数-中等

- python 实现
class Solution: def openLock(self, deadends: List[str], target: str) -> int: # block[j] 向上拨动一次 def plusOne(block, j): block = [int(s) for s in block] if block[j] == 9: block[j] = 0 else: block[j] += 1 return ''.join([str(b) for b in block]) # block[j] 向下拨动一次 def minusOne(block, j): block = [int(s) for s in block] if block[j] == 0: block[j] = 9 else: block[j] -= 1 return ''.join([str(b) for b in block]) # 死亡密码记录 deads = set(deadends) # 记录已经访问过的密码,路径 , 防止走回头路 # 后面添加记得 list--> visited = set(['0000']) # 使用队列,记录当前步数下的密码 queue = ['0000'] # 从起点开始 BFS step = 0 while queue: queue_size = len(queue) # 将当前队列中的节点向周围扩散 for i in range(queue_size): curNode = queue.pop(0) # 判断是否到达终点 if curNode in deads: continue if curNode == target: return step # 将一个节点的未遍历相邻节点加入队列, 8个相邻 for j in range(4): up = plusOne(curNode, j) # 限制不走回头路 if up not in visited: visited.add(up) queue.append(up) print('up_add:', up) down = minusOne(curNode, j) if down not in visited: visited.add(down) queue.append(down) print('down_add:', down) # 步数增加 step += 1 # 遍历完毕,未找到合适路径 return -1
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
102. 二叉树的层序遍历-中等
102. 二叉树的层序遍历 给你一个二叉树,请你返回其按 层序遍历 得到的节点值。 (即逐层地,从左到右访问所有节点)。 示例: 二叉树:[3,9,20,null,null,15,7], 3 / \ 9 20 / \ 15 7 返回其层次遍历结果: [ [3], [9,20], [15,7] ]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
# 套框架: 终止条件发生变化 ,不再是选择最短路径 # Definition for a binary tree node. # class TreeNode: # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution: def levelOrder(self, root: TreeNode) -> List[List[int]]: # 思路: 使用队列,BFS res = [] if not root: return res queue = [root] while queue: line_res = [] # 存储当前层的节点 queue_size = len(queue) # 将当前队列节点向四周扩散 for i in range(queue_size): curNode = queue.pop(0) # 划重点: 判断是否到达终点 # if curNode: 不必判断: curNode.left 和 curNode.right 都已经满足了, # curNode必然满足; line_res.append(curNode.val) # 将相邻节点加入 if curNode.left: queue.append(curNode.left) if curNode.right: queue.append(curNode.right) # 将一层节点加入result res.append(line_res) return res
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
107. 二叉树的层次遍历 II-简单
107. 二叉树的层次遍历 II 给定一个二叉树,返回其节点值自底向上的层次遍历。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历) 例如: 给定二叉树 [3,9,20,null,null,15,7], 3 / \ 9 20 / \ 15 7 返回其自底向上的层次遍历为: [ [15,7], [9,20], [3] ]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
# 层次遍历结果反转 # Definition for a binary tree node. # class TreeNode: # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution: def levelOrderBottom(self, root: TreeNode) -> List[List[int]]: # 思路: 使用队列,BFS res = [] if not root: return res queue = [root] while queue: line_res = [] # 存储当前层的节点 queue_size = len(queue) # 将当前队列节点向四周扩散 for i in range(queue_size): curNode = queue.pop(0) # 划重点: 判断是否到达终点 # if curNode: 不必判断: curNode.left 和 curNode.right 都已经满足了, curNode必然满足; line_res.append(curNode.val) # 将相邻节点加入 if curNode.left: queue.append(curNode.left) if curNode.right: queue.append(curNode.right) # 将一层节点加入result res.append(line_res) return res[::-1]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
103. 二叉树的锯齿形层次遍历-中等
103. 二叉树的锯齿形层次遍历 给定一个二叉树,返回其节点值的锯齿形层次遍历。 (即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。 例如: 给定二叉树 [3,9,20,null,null,15,7], 3 / \ 9 20 / \ 15 7 返回锯齿形层次遍历如下: [ [3], [20,9], [15,7] ]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
# Definition for a binary tree node. # class TreeNode: # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution: def zigzagLevelOrder(self, root: TreeNode) -> List[List[int]]: # 层次遍历,使用队列 res = [] if not root: return res queue = [root] row = 1 while queue: line_res = [] queue_size = len(queue) # 当前队列节点向四周扩散 for i in range(queue_size): curNode = queue.pop(0) # 划重点: 判断是否到达终点 line_res.append(curNode.val) if curNode.left: queue.append(curNode.left) if curNode.right: queue.append(curNode.right) if row % 2 == 0: # line_res = sorted(line_res, reverse = True) 按元素排序,出错 line_res.reverse() # line_res = line_res[::-1] print(line_res) row += 1 res.append(line_res) return res
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
101. 对称二叉树-简单
101. 对称二叉树 给定一个二叉树,检查它是否是镜像对称的。 例如,二叉树 [1,2,2,3,4,4,3] 是对称的。 1 / \ 2 2 / \ / \ 3 4 4 3 但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的: 1 / \ 2 2 \ \ 3 3
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
# 非递归 方法 # Definition for a binary tree node. # class TreeNode: # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution: def isSymmetric(self, root: TreeNode) -> bool: # 非递归: BFS判断当前层元素是否为对称 # 时间复杂度: # 空间复杂度: res = [] if not root: return True queue = [root] row = 1 while queue: line_res = [] queue_size = len(queue) # 将当前队列元素向四周扩散 for i in range(queue_size): curNode = queue.pop(0) # 划重点: 判断是否到达终止 if curNode: line_res.append(curNode.val) queue.append(curNode.left) queue.append(curNode.right) else: line_res.append('null') # 判断当前层是否符合镜像二叉树要求 if len(line_res) % 2 != 0 and row != 1: return False back = line_res[::-1] if line_res != back: return False row += 1 return True
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
# 递归方法 # Definition for a binary tree node. # class TreeNode: # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution: def isMirror(self,t1,t2): if not t1 and not t2: return True if not t1 or not t2: return False return t1.val == t2.val and self.isMirror(t1.right,t2.left) and self.isMirror(t1.left,t2.right) def isSymmetric(self, root: TreeNode) -> bool: return self.isMirror(root,root)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
200.岛屿数量-中等
200. 岛屿数量 给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。 岛屿总是被水包围,并且每座岛屿只能由水平方向或竖直方向上相邻的陆地连接形成。 此外,你可以假设该网格的四条边均被水包围。 示例 1: 输入: 11110 11010 11000 00000 输出: 1 示例 2: 输入: 11000 11000 00100 00011 输出: 3 解释: 每座岛屿只能由水平和/或竖直方向上相邻的陆地连接而成。
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
大佬解答1-DFS + BFS + 并查集(Python 代码、Java 代码)

说明:以下介绍的算法,除了并查集以外,DFS 和 BFS 都属于很基础的算法内容,也非常好理解,写法也相对固定,读者需要多写,发现并记录自己的问题,我也是在写了几遍甚至是在写本题解的过程中,才发现出自己的问题。
这道题是可以使用一个经典的算法来解决的,那就是 Flood fill,以下的定义来自 维基百科:Flood fill 词条。
Flood fill 算法是从一个区域中提取若干个连通的点与其他相邻区域区分开(或分别染成不同颜色)的经典 算法。因为其思路类似洪水从一个区域扩散到所有能到达的区域而得名。在 GNU Go 和 扫雷 中,Flood Fill算法被用来计算需要被清除的区域。
“Flood” 我查了一下,作为动词是 “淹没;充满” 的意思,作为名词是 “洪水” 的意思。下面我们简单解释一下这个算法:
从一个区域中提取若干个连通的点与其他相邻区域区分开
从一个点扩散开,找到与其连通的点,这不是什么高深的算法,其实就是从一个点开始,进行一次 “深度优先遍历” 或者 “广度优先遍历”,通过 “深度优先遍历” 或者 “广度优先遍历” 发现一片连着的区域,对于这道题来说,就是从一个是 “陆地” 的格子开始进行一次 “深度优先遍历” 或者 “广度优先遍历”,把与之相连的所有的格子都标记上,视为发现了一个 “岛屿”。
说明:这里做 “标记” 的意思是,通过 “深度优先遍历” 或者 “广度优先遍历” 操作,我发现了一个新的格子,与起始点的那个格子是连通的,我们视为 “标记” 过,也可以说 “被访问过”。
那么每一次进行 “深度优先遍历” 或者 “广度优先遍历” 的条件就是:
1、这个格子是陆地 1,如果是水域 0 就无从谈论 “岛屿”;
2、这个格子不能是之前发现 “岛屿” 的过程中执行了 “深度优先遍历” 或者 “广度优先遍历” 操作,而被标记的格子(这句话说得太拗口了,大家意会即可,意会不了不是您的问题,是我表达的问题,直接看代码会清楚很多)。
方法一:深度优先遍历
方法二:广度优先遍历
除了 “深度优先遍历”,你还可以使用 “广度优先遍历”,此时你就不用回溯了。“广度优先遍历” 需要一个 “辅助队列”。
(温馨提示:下面的幻灯片中,有几页上有较多的文字,可能需要您停留一下,可以点击右下角的后退 “|◀” 或者前进 “▶|” 按钮控制幻灯片的播放。)












在写 “广度优先遍历” 的时候,要注意一点:
所有加入队列的结点,都应该马上被标记为 “已经访问”,否则有可能会被重复加入队列。
我一开始在编写的时候,等到队列出队的时候才标记 “已经访问”,事实上,这种做法是错误的。因为如果不在刚刚入队列的时候标记 “已经访问”,相同的结点很可能会重复入队,如果你遇到“超时”的提示,你不妨把你的队列打印出来看一下,就很清楚看到我说的这一点。
大佬代码:
from typing import List from collections import deque class Solution: # x-1,y # x,y-1 x,y x,y+1 # x+1,y # 方向数组,它表示了相对于当前位置的 4 个方向的横、纵坐标的偏移量,这是一个常见的技巧 directions = [(-1, 0), (0, -1), (1, 0), (0, 1)] def numIslands(self, grid: List[List[str]]) -> int: m = len(grid) # 特判 if m == 0: return 0 n = len(grid[0]) marked = [[False for _ in range(n)] for _ in range(m)] count = 0 # 从第 1 行、第 1 格开始,对每一格尝试进行一次 DFS 操作 for i in range(m): for j in range(n): # 只要是陆地,且没有被访问过的,就可以使用 BFS 发现与之相连的陆地,并进行标记 if not marked[i][j] and grid[i][j] == '1': # count 可以理解为连通分量,你可以在广度优先遍历完成以后,再计数, # 即这行代码放在【位置 1】也是可以的 count += 1 queue = deque() queue.append((i, j)) # 注意:这里要标记上已经访问过 marked[i][j] = True while queue: cur_x, cur_y = queue.popleft() # 得到 4 个方向的坐标 for direction in self.directions: new_i = cur_x + direction[0] new_j = cur_y + direction[1] # 如果不越界、没有被访问过、并且还要是陆地,我就继续放入队列,放入队列的同时,要记得标记已经访问过 if 0 <= new_i < m and 0 <= new_j < n and not marked[new_i][new_j] and grid[new_i][new_j] == '1': queue.append((new_i, new_j)) #【特别注意】在放入队列以后,要马上标记成已经访问过,语义也是十分清楚的:反正只要进入了队列,你迟早都会遍历到它 # 而不是在出队列的时候再标记 #【特别注意】如果是出队列的时候再标记,会造成很多重复的结点进入队列,造成重复的操作,这句话如果你没有写对地方,代码会严重超时的 marked[new_i][new_j] = True #【位置 1】 return count if __name__ == '__main__': grid = [['1', '1', '1', '1', '0'], ['1', '1', '0', '1', '0'], ['1', '1', '0', '0', '0'], ['0', '0', '0', '0', '0']] solution = Solution() result = solution.numIslands(grid) print(result)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
自己python再次实现一次(基本抄大佬)
class Solution: # x-1,y # x,y-1 x,y x,y+1 # x+1,y # 方向数组,它表示了相对于当前位置的 4 个方向的横、纵坐标的偏移量,这是一个常见的技巧 directions = [(-1, 0), (0, -1), (1, 0), (0, 1)] def numIslands(self, grid: List[List[str]]) -> int: # 求岛屿数量: 将二维网格看作图, 本质上是搜索满足条件的点。 # 怎样识别使用BFS? 搜索邻接岛屿 # BFS框架 # res = [] # queue = [root] // 队列数据结构 # # // 使用队列进行遍历 # while queue: # queue_size = len(queue) # # // 将当前队列元素向四周扩散 # for i in range(queue_szie): # curNode = queue.pop(0) # # // 划重点: 判断是否到达终止位置 # if curNode is target: # return step # ... # # // 当前节点相邻节点添加 # for (Node x in curNode.adj()): # // 去除已经访问等干扰因素 # if Node x not in visited: # queue.append(x) # visited.append(x) # // 划重点: 更新步数 # step += 1 ''' grid list: 待搜索图 return num : 岛屿数量 ''' # 边界处理: grid:[] if not grid: return 0 rows, cols = len(grid), len(grid[0]) # marked: 类似于 visited, 用来标注 坐标是否访问过 marked = [[False for _ in range(cols)] for _ in range(rows)] count = 0 # 由于 start、target都未知, 所有节点都可能为 start, 所以需要遍历整个网格,选择start # 从第一行、第一格 开始, 对每一个格子尝试进行一次 BFS 操作 for row in range(rows): for col in range(cols): # 只要是 陆地(value=1), 且未被访问过的, 就可以使用 BFS 发现与之相连的陆地, 并进行标记 if not marked[row][col] and grid[row][col] == '1': # count 可以理解为联通分量, 可以在 BFS 遍历完成之后(【位置1】),再计数,也可以在此处(必定有一个结果) # // 进入 BFS的标准化模板 queue = [(row, col)] # 注意这里要标记已经访问过 marked[row][col] = True # 利用队列进行遍历 while queue: # queue_size: 本质作用, 记录一步或者一层 队列中有几个元素; 如果结果不结算层、不计算多少步, 其实也没必要的; queue_size = len(queue) # 划重点: 将当前队列中的所有节点向四周 for i in range(queue_size): curNode = queue.pop(0) curNode_x, curNode_y = curNode # print(curNode_x, curNode_y) # 划重点: 判断是否到达终止条件, 本题终止为: 队列中元素为空 # 划重点: 当前节点的相邻节点加入, 记得判断是否访问, 能不能访问 for direction in self.directions: new_row = curNode_x + direction[0] new_col = curNode_y + direction[1] # print('new_row, new_col', new_row, new_col) # 如果1) 不越界; 2) 未被访问; 3) 为 陆地; 继续放入队列, 放入队列同时标注: 已访问过 if 0<=new_row<rows and 0<=new_col<cols and not marked[new_row][new_col] and grid[new_row][new_col] == '1': queue.append((new_row, new_col)) # 特别注意: 在放入队列之后,要马上标记’已访问过‘, 语义很清楚: 进了队列都会遍历; # 入队列时候记得标记; # 特别注意: 如果是出队列时候标记, 会造成很多重复节点进入队列,造成重复操作,超时; marked[new_row][new_col] = True # 【位置1】: 此时队列为空, 一次BFS结束; count += 1 # print(row, col, count) # print(marked) count += 1 # 遍历所有网格结束; return count
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
本题一些新的启发、创新
1. BFS搜索中 start、target均未知, 需要遍历 grid网格中所有点, 从当前点作为 start进行BFS;
2. BFS中计数问题: 每次BFS必有一个结果;
3. BFS框架中 队列中元素数量统计是为了 记录当前层、当前行、当前步骤 , 如果问题中不涉及,可以不考虑,最终遍历完 队列queue就行;
4. visited列表、marked 网格grid都是必不可少的,代码可读性会很强;
5. directions = [(-1, 0), (0, -1), (1, 0), (0, 1)]向四个方向遍历相邻节点的学习
- 1
- 2
- 3
- 4
- 5
542. 01 矩阵-中等-未AC
1162. 地图分析-中等-未AC
自己一些思路和思考
1. 典型网格问题 BFS, start节点可以有很多,
2. 没想明白最大距离怎么计算?
- 1
- 2
10. 涂色问题、连通块问题、01宫格问题、全排列问题
695. 岛屿的最大面积-中等-AC
695. 岛屿的最大面积- 给定一个包含了一些 0 和 1 的非空二维数组 grid 。 一个 岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在水平或者竖直方向 上相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。 找到给定的二维数组中最大的岛屿面积。(如果没有岛屿,则返回面积为 0 。) 示例 1: [[0,0,1,0,0,0,0,1,0,0,0,0,0], [0,0,0,0,0,0,0,1,1,1,0,0,0], [0,1,1,0,1,0,0,0,0,0,0,0,0], [0,1,0,0,1,1,0,0,1,0,1,0,0], [0,1,0,0,1,1,0,0,1,1,1,0,0], [0,0,0,0,0,0,0,0,0,0,1,0,0], [0,0,0,0,0,0,0,1,1,1,0,0,0], [0,0,0,0,0,0,0,1,1,0,0,0,0]] 对于上面这个给定矩阵应返回 6。注意答案不应该是 11 ,因为岛屿只能包含水平或垂直的四个方向的 1 。 示例 2: [[0,0,0,0,0,0,0,0]] 对于上面这个给定的矩阵, 返回 0。
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 自己按照大佬思路实现
class Solution: # 套路: 沿着四个方向遍历 directions = [(-1, 0), (0, -1), (1, 0), (0, 1)] def maxAreaOfIsland(self, grid: List[List[int]]) -> int: # 经典BFS, 同样问题, start可以是任意节点; 保留各个 queue搜索到的 max(areas) if not grid: return 0 # res: 记录每次搜索到的岛屿面机 res = [] rows, cols = len(grid), len(grid[0]) visited = [[False for _ in range(cols)] for _ in range(rows)] # BFS框架 def BFS(start_x, start_y): area = 1 queue = [(start_x, start_y)] visited[start_x][start_y] = True # 开始使用队列遍历 while queue: queue_size = len(queue) # 划重点: 将队列元素向四周扩散 for i in range(queue_size): curNode = queue.pop(0) curNode_x, curNode_y = curNode # 划重点: 判断是否终止 # 划重点: 当前节点相邻节点加入队列 for direction in self.directions: new_row = curNode_x + direction[0] new_col = curNode_y + direction[1] # 新节点进行条件判断 # 如果: 1)不越界; 2) 土地; 3)未被访问; 继续放入队列,并且标注已访问 if 0<=new_row<rows and 0<=new_col<cols and grid[new_row][new_col] == 1 and not visited[new_row][new_col]: queue.append((new_row, new_col)) area += 1 visited[new_row][new_col] = True res.append(area) for row in range(rows): for col in range(cols): if grid[row][col] == 1 and not visited[row][col]: BFS(row, col) return max(res) if res else 0
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
Offer 13. 机器人的运动范围-中等-自己AC
剑指 Offer 13. 机器人的运动范围
地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,
它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。
例如,当k为18时,机器人能够进入方格 [35, 37] ,因为3+5+3+7=18。但它不能进入方格 [35, 38],
因为3+5+3+8=19。请问该机器人能够到达多少个格子?
示例 1:
输入:m = 2, n = 3, k = 1
输出:3
示例 2:
输入:m = 3, n = 1, k = 0
输出:1
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
自己首先思路
1. 简单BFS题目, 且给定起点 start , 难点在于 限制条件的理解;
- 1
class Solution: # 网格BFS周围套路 directions = [(-1, 0), (0, -1), (1, 0), (0, 1)] def sumBit(self, x, y): s = list(map(str,[x,y])) #将a,b移入列表中 s1 = list(map(int,list(s[0]))) s2 = list(map(int, list(s[1]))) return sum(s1) + sum(s2) def movingCount(self, m: int, n: int, k: int) -> int: # 思路: BFS搜索一次结果; # 套模板就行 if m <= 0 or n <= 0 or k < 0: return 0 # 初始化grid, visited grid = [[0 for _ in range(n)] for _ in range(m)] visited = [[False for _ in range(n)] for _ in range(m)] queue = [(0, 0)] visited[0][0] = True res = 1 while queue: queue_size = len(queue) # 划重点: 当前队列元素向四周扩散 for i in range(queue_size): curNode = queue.pop(0) curNode_x, curNode_y = curNode # 划重点: 判断是否到达终止条件 # 划重点: 将当前队列节点 相邻节点加入队列 for direction in self.directions: new_row = curNode_x + direction[0] new_col = curNode_y + direction[1] # 判断节点的可行性 # 1) 不越界; 2) 未访问; 3) 满足 数位之和小于K if 0<=new_row<m and 0<=new_col<n and not visited[new_row][new_col] and self.sumBit(new_row, new_col) <= k: queue.append((new_row, new_col)) res += 1 visited[new_row][new_col] = True return res
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
733. 图像渲染-简单
有一幅以二维整数数组表示的图画,每一个整数表示该图画的像素值大小,数值在 0 到 65535 之间。
给你一个坐标 (sr, sc) 表示图像渲染开始的像素值(行 ,列)和一个新的颜色值 newColor,让你重新上色这幅图像。
输入:
image = [[1,1,1],[1,1,0],[1,0,1]]
sr = 1, sc = 1, newColor = 2
输出: [[2,2,2],[2,2,0],[2,0,1]]
解析:
在图像的正中间,(坐标(sr,sc)=(1,1)),
在路径上所有符合条件的像素点的颜色都被更改成2。
注意,右下角的像素没有更改为2,
因为它不是在上下左右四个方向上与初始点相连的像素点。
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
python- BFS、DFS
class Solution: def floodFill(self, image: List[List[int]], sr: int, sc: int, newColor: int) -> List[List[int]]: # 思路1: BFS # 思路2: DFS, 本质依然是找最大联通面积 directions = [(-1, 0), (1, 0), (0, 1), (0, -1)] def BFS(image, sr, sc, newColor, originColor): # 初始化queue queue = [(sr, sc)] image[sr][sc] = newColor while queue: queue_len = len(queue) # 换重点: 队列中元素像四周扩散 for i in range(queue_len): curNode = queue.pop(0) curNode_row, curNode_col = curNode # 划重点: 终止条件判断 # 划重点: 当前节点向 邻居扩散 for direction in directions: new_row = curNode_row + direction[0] new_col = curNode_col + direction[1] # 合法性判断: 1) 不越界; 2) 未访问; 3) 等于orginCol if 0<=new_row<rows and 0<=new_col<cols and image[new_row][new_col] == originColor: queue.append((new_row, new_col)) image[new_row][new_col] = newColor return image def DFS(image, sr, sc, newColor, originColor): image[sr][sc] = newColor for direction in directions: new_sr = sr + direction[0] new_sc = sc + direction[1] # 合法性判断: 1) 不越界; 2) 未访问; 3) 等于 if 0<=new_sr<rows and 0<=new_sc<cols and image[new_sr][new_sc] == originColor: DFS(image, new_sr, new_sc, newColor, originColor) return image if not image: return None rows, cols = len(image), len(image[0]) originColor = image[sr][sc] if newColor == originColor: return image return DFS(image, sr, sc, newColor, originColor) # return BFS(image, sr, sc, newColor, originColor)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
1293. 网格中的最短路径

- python实现:
class Solution: def shortestPath(self, grid: List[List[int]], k: int) -> int: # 思路: BFS, 但是对于具体障碍的清除没想清楚; directions = [(-1, 0), (1, 0), (0, 1), (0, -1)] m, n = len(grid), len(grid[0]) if m == 1 and n == 1: return 0 k = min(k, m+n-3) visited = set([0, 0, k]) queue = [[0, 0, k]] step = 0 while queue: queue_len = len(queue) print(queue) # 当前queue中元素分别向四周扩散 for i in range(queue_len): curNode = queue.pop(0) curNode_x, curNode_y, rest = curNode # 终止条件 if curNode_x == m-1 and curNode_y == n - 1: return step # 当前节点向四周进行扩散; for direction in directions: new_x = curNode_x + direction[0] new_y = curNode_y + direction[1] # 队列加入元素合法性判断: 1) 不越界; if 0<=new_x<m and 0<=new_y<n: if grid[new_x][new_y] == 0 and (new_x, new_y, rest) not in visited: queue.append((new_x, new_y, rest)) visited.add((new_x, new_y, rest)) elif grid[new_x][new_y] == 1 and rest>0 and (new_x, new_y, rest-1) not in visited: queue.append((new_x, new_y, rest-1)) visited.add((new_x, new_y, rest-1)) # 这时候看看具体怎么需要,走一步算一步可能放这了。 step = step + 1 return -1
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
⭐⭐⭐DFS-相关题目
200.岛屿数量-中等
200. 岛屿数量 给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。 岛屿总是被水包围,并且每座岛屿只能由水平方向或竖直方向上相邻的陆地连接形成。 此外,你可以假设该网格的四条边均被水包围。 示例 1: 输入: 11110 11010 11000 00000 输出: 1 示例 2: 输入: 11000 11000 00100 00011 输出: 3 解释: 每座岛屿只能由水平和/或竖直方向上相邻的陆地连接而成。
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
参考 大佬解答1-DFS + BFS + 并查集(Python 代码、Java 代码)
方法一:深度优先遍历
(温馨提示:下面的幻灯片中,有几页上有较多的文字,可能需要您停留一下,可以点击右下角的后退 “|◀” 或者前进 “▶|” 按钮控制幻灯片的播放。)


















参考大佬代码:
from typing import List class Solution: # x-1,y # x,y-1 x,y x,y+1 # x+1,y # 方向数组,它表示了相对于当前位置的 4 个方向的横、纵坐标的偏移量,这是一个常见的技巧 directions = [(-1, 0), (0, -1), (1, 0), (0, 1)] def numIslands(self, grid: List[List[str]]) -> int: m = len(grid) # 特判 if m == 0: return 0 n = len(grid[0]) marked = [[False for _ in range(n)] for _ in range(m)] count = 0 # 从第 1 行、第 1 格开始,对每一格尝试进行一次 DFS 操作 for i in range(m): for j in range(n): # 只要是陆地,且没有被访问过的,就可以使用 DFS 发现与之相连的陆地,并进行标记 if not marked[i][j] and grid[i][j] == '1': # count 可以理解为连通分量,你可以在深度优先遍历完成以后,再计数, # 即这行代码放在【位置 1】也是可以的 count += 1 self.__dfs(grid, i, j, m, n, marked) # 【位置 1】 return count def __dfs(self, grid, i, j, m, n, marked): marked[i][j] = True for direction in self.directions: new_i = i + direction[0] new_j = j + direction[1] if 0 <= new_i < m and 0 <= new_j < n and not marked[new_i][new_j] and grid[new_i][new_j] == '1': self.__dfs(grid, new_i, new_j, m, n, marked) if __name__ == '__main__': grid = [['1', '1', '1', '1', '0'], ['1', '1', '0', '1', '0'], ['1', '1', '0', '0', '0'], ['0', '0', '0', '0', '0']] solution = Solution() result = solution.numIslands(grid) print(result)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
自己python再次实现一次(基本抄大佬)
- 1
⭐⭐⭐回溯
白话算法
回溯法(back tracking)(探索与回溯法)是一种选优搜索法,又称为试探法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。
白话:回溯法可以理解为通过选择不同的岔路口寻找目的地,一个岔路口一个岔路口的去尝试找到目的地。如果走错了路,继续返回来找到岔路口的另一条路,直到找到目的地。
知乎-回溯算法套路详解
经典问题列表
框架与解读(上述链接复制,方便自己阅读,瑞斯拜大佬)
回溯算法框架。解决一个回溯问题,实际上就是一个**决策树的遍历过程**。你只需要思考 3 个问题:
1、路径:也就是已经做出的选择。
2、选择列表:也就是你当前可以做的选择。
3、结束条件:也就是到达决策树底层,无法再做选择的条件。
如果你不理解这三个词语的解释,没关系,我们后面会用「全排列」和「N 皇后问题」这两个经典的回溯算法问题来帮你理解这些词语是什么意思,现在你先留着印象。
- 1
- 2
- 3
- 4
- 5
- 6
- 7
代码方面,回溯算法的框架:
result = []
def backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
其核心就是 for 循环里面的递归,在递归调用之前「做选择」,在递归调用之后「撤销选择」,特别简单。
什么叫做选择和撤销选择呢,这个框架的底层原理是什么呢?下面我们就通过「全排列」这个问题来解开之前的疑惑,详细探究一下其中的奥妙!
一、全排列问题: 46: 全排列-中等
46. 全排列---中等
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
示例:
输入: [1,2,3
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
我们在高中的时候就做过排列组合的数学题,我们也知道 n 个不重复的数,全排列共有 n! 个。
PS:为了简单清晰起见,我们这次讨论的全排列问题不包含重复的数字。
那么我们当时是怎么穷举全排列的呢?比方说给三个数 [1,2,3],你肯定不会无规律地乱穷举,一般是这样:
先固定第一位为 1,然后第二位可以是 2,那么第三位只能是 3;然后可以把第二位变成 3,第三位就只能是 2 了;然后就只能变化第一位,变成 2,然后再穷举后两位……
其实这就是回溯算法,我们高中无师自通就会用,或者有的同学直接画出如下这棵回溯树:

只要从根遍历这棵树,记录路径上的数字,其实就是所有的全排列。我们不妨把这棵树称为回溯算法的「决策树」。
为啥说这是决策树呢,因为你在每个节点上其实都在做决策。比如说你站在下图的红色节点上:

你现在就在做决策,可以选择 1 那条树枝,也可以选择 3 那条树枝。为啥只能在 1 和 3 之中选择呢?因为 2 这个树枝在你身后,这个选择你之前做过了,而全排列是不允许重复使用数字的。
现在可以解答开头的几个名词:[2] 就是「路径」,记录你已经做过的选择;[1,3] 就是「选择列表」,表示你当前可以做出的选择;「结束条件」就是遍历到树的底层,在这里就是选择列表为空的时候。
如果明白了这几个名词,可以把**「路径」和「选择」列表作为决策树上每个节点的属性** ,比如下图列出了几个节点的属性:

我们定义的 backtrack 函数其实就像一个指针,在这棵树上游走,同时要正确维护每个节点的属性,每当走到树的底层,其「路径」就是一个全排列。
再进一步,如何遍历一棵树?这个应该不难吧。回忆一下之前「学习数据结构的框架思维」写过,各种搜索问题其实都是树的遍历问题,而多叉树的遍历框架就是这样:
# 自己理解: 本质还是 树的搜索过程,只是每个树的节点带了属性(【路径】、【选择列表】), 然后遍历到每个节点时候对于属性进行判断,如果节点满足【结束条件】,则返回,然后进一步修改,节点的属性,迭代遍历;
void traverse(TreeNode root) {
for (TreeNode child : root.childern)
// 前序遍历需要的操作
traverse(child);
// 后序遍历需要的操作
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
而所谓的前序遍历和后序遍历,他们只是两个很有用的时间点,我给你画张图你就明白了:

现在,你是否理解了回溯算法的这段核心框架?

for 选择 in 选择列表:
# 做选择
将该选择从选择列表移除
路径.add(选择)
backtrack(路径, 选择列表)
# 撤销选择
路径.remove(选择)
将该选择再加入选择列表
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
我们只要在递归之前做出选择,在递归之后撤销刚才的选择,就能正确得到每个节点的选择列表和路径。
下面,直接看全排列代码:
python实现
# python 代码 class Solution: def permute(self, nums: List[int]) -> List[List[int]]: # // 路径:记录在 track 中 # // 选择列表:nums 中不存在于 track 的那些元素 # // 结束条件:nums 中的元素全都在 track 中出现 def trackBack(nums,track): # (路径, 选择列表) # 触发结束条件 if len(track) == len(nums): res.append(track[:]) # 需要传递下track的拷贝,否则对track的修改会影响到结果 return None # // 遍历选择列表,做选择的过程 for i in nums: # // 排除不合法的选择 if i in track: continue # // 做选择 track.append(i) # // 进入下一层决策树 trackBack(nums,track) # // 取消选择,'回溯'过程 track.pop() res = [] # 最终 遍历得到 多个路径 的结果存储 track = [] # 记录当前 路径 trackBack(nums,track) return res
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
我们这里稍微做了些变通,没有显式记录「选择列表」,而是通过 nums 和 track 推导出当前的选择列表:

至此,我们就通过全排列问题详解了回溯算法的底层原理。当然,这个算法解决全排列不是很高效,应为对链表使用 contains 方法需要 O(N) 的时间复杂度。有更好的方法通过交换元素达到目的,但是难理解一些,这里就不写了,有兴趣可以自行搜索一下。
但是必须说明的是,不管怎么优化,都符合回溯框架,而且时间复杂度都不可能低于 O(N!),因为穷举整棵决策树是无法避免的。这也是回溯算法的一个特点,不像动态规划存在重叠子问题可以优化,回溯算法就是纯暴力穷举,复杂度一般都很高。
二.N皇后问题: 51: N皇后问题-hard
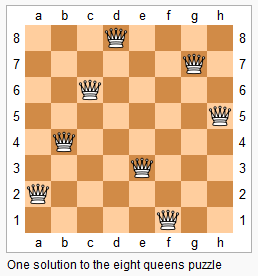
51. N皇后--困难 n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。 上图为 8 皇后问题的一种解法。 给定一个整数 n,返回所有不同的 n 皇后问题的解决方案。 每一种解法包含一个明确的 n 皇后问题的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。 示例: 输入: 4 输出: [ [".Q..", // 解法 1 "...Q", "Q...", "..Q."], ["..Q.", // 解法 2 "Q...", "...Q", ".Q.."] ] 解释: 4 皇后问题存在两个不同的解法。
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
这个问题很经典了,简单解释一下:给你一个 N×N 的棋盘,让你放置 N 个皇后,使得它们不能互相攻击。
PS:皇后可以攻击同一行、同一列、左上左下右上右下四个方向的任意单位。
这个问题本质上跟全排列问题差不多,决策树的每一层表示棋盘上的每一行;每个节点可以做出的选择是,在该行的任意一列放置一个皇后。
python实现
时间复杂度分析:
1. N**(N)----对应于搜索树分析
空间复杂度分析:
1. 初始化过程使用N**2
2. 存储中间结果: N**2
3. 最终结果: res*N**2
- 1
- 2
- 3
- 4
- 5
- 6
# python class Solution: # 时间复杂度分析: # 空间复杂度分析: N**2 def solveNQueens(self, n: int) -> List[List[str]]: # 思路: 经典回溯问题: 难点在于 坐标 p[i][j] 能否放皇后问题的判断; # 首先明白: 同行只有一个皇后,同列也是只有一个皇后 # 回溯问题大框架: # 1. 思考三个问题: 1) 路径: 已经做出的选择 2) 选择列表: 当前可以做的选择(排除不能做的选择) 3) 结束条件: 到达决策树底层, 无法再做选择的条件; # 2. 代码框架 # result = [] # def trackBack(路径, 选择列表): # if 满足结束条件: # 递归终止条件 # result.append(路径) # return None # 找到一个解空间,继续; # # for 选择 in 选择列表: # 做选择 # trackBack(当前路径, 当前选择列表) # 撤销选择,回溯操作 # trackBack(路径, 选择列表) # 调用 回溯算法 # return result # 回溯算法: 因为每行中仅有一个皇后,所以路径只需要记录当前行数就可以; def trackBack(board, row): # 回溯步骤1: # if 满足条件: # res.append(路径) # 路径本题指: 整个棋盘元素 # return # // 触发结束条件 if row == len(board): tmp_list = [] # 将 二维棋盘转换为1维列表,进一步加入最终结果 for res_row in board: tmp_line_res = ''.join(res_row) tmp_list.append(tmp_line_res) res.append(tmp_list) return None # 回溯步骤2: # for 选择 in 选择列表: # 排除不合法选择 # 做选择 # trackBack(路径, 选择列表) 路径: row 选择列表: board # 撤销选择,回溯 # // 对于每一行遍历,进一步做选择,选择哪一列 for col in range(len(board[0])): # // 排除不合法路径: 各个回溯算法主要不同之处 if not isVaild(board, row, col): # 判断当前未知 row, col 在(当前已知信息遍历路径+现有棋盘结果)能否放置皇后; 如果不能则排除; 如果可以则继续 continue # // 做选择, 棋盘布局发生变化, 对应 路径、选择列表发生变化 board[row][col] = 'Q' # // 当前行决策完成,进入下一行进行决策 trackBack(board, row+1) # 当前位置执行、递归结束, 撤销选择, 回溯 board[row][col] = '.' # 至此,回溯算法结束; def isVaild(board, row, col): # 条件1: 列不能有皇后 # 条件2: 右上方对角线不能有皇后 # 条件3:左上方对角线不能有皇后 # 3条件都满足才可以设置皇后; # 检查列 是否有皇后冲突, 当前列,从第一行到当前行,不能设置 皇后 for i in range(row): if board[i][col] == 'Q': return False # 检查右上方对角线 是否有皇后冲突, 对角线条件[...] r_row, r_col = row, col while r_row > 0 and r_col < n-1: #终止条件: r_row = 0, r_col = n -1 r_row -= 1 r_col += 1 if board[r_row][r_col] == 'Q': return False # 检查左上方对角线 是否有皇后冲突, 对角线条件 l_row, l_col = row, col while l_row > 0 and l_col > 0: l_row -= 1 l_col -= 1 if board[l_row][l_col] == 'Q': return False return True # 初始化二维棋盘: 初始化. , 后面有皇后: Q board = [['.']*n for _ in range(n)] # 最终结果: [[棋盘1布局], [棋盘2布局], [棋盘3布局], ...] , 元素为: 正确放置皇后的棋盘; res = [] trackBack(board, 0) # board: 选择列表 0: 当前路径(row) return res
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
思考: 如何进一步优化? 如何进行剪枝?
左上方、右上方的判断过程: 不能进一步进行优化;
判断
- 1
- 2
- 3
函数 backtrack 依然像个在决策树上游走的指针,通过 row 和 col 就可以表示函数遍历到的位置,通过 isValid 函数可以将不符合条件的情况剪枝: 最差时间复杂度O(N^N)

如果直接给你这么一大段解法代码,可能是懵逼的。但是现在明白了回溯算法的框架套路,还有啥难理解的呢?无非是1. 改改做选择的方式,排除不合法选择的方式而已,只要框架存于心,你面对的只剩下小问题了。
当 N = 8 时,就是八皇后问题,数学大佬高斯穷尽一生都没有数清楚八皇后问题到底有几种可能的放置方法,但是我们的算法只需要一秒就可以算出来所有可能的结果。
不过真的不怪高斯。这个问题的复杂度确实非常高,看看我们的决策树,虽然有 isValid 函数剪枝,但是最坏时间复杂度仍然是 O(N^(N+1)),而且无法优化。如果 N = 10 的时候,计算就已经很耗时了。
有的时候,我们并不想得到所有合法的答案,只想要一个答案,怎么办呢?比如解数独的算法,找所有解法复杂度太高,只要找到一种解法就可以。
其实特别简单,只要稍微修改一下回溯算法的代码即可:
// 函数找到一个答案后就返回 true bool backtrack(vector<string>& board, int row) { // 触发结束条件 if (row == board.size()) { res.push_back(board); return true; # 如果出现正确答案则终止 } ... for (int col = 0; col < n; col++) { ... board[row][col] = 'Q'; if (backtrack(board, row + 1)) # 进行一次判断,如果选择正确则发生终止; return true; board[row][col] = '.'; } return false; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
这样修改后,只要找到一个答案,for 循环的后续递归穷举都会被阻断。也许你可以在 N 皇后问题的代码框架上,稍加修改,写一个解数独的算法?
三、最后总结
回溯算法就是个多叉树的遍历问题,关键就是在前序遍历和后序遍历的位置做一些操作,算法框架如下:
def backtrack(...):
for 选择 in 选择列表:
做选择
backtrack(...)
撤销选择
- 1
- 2
- 3
- 4
- 5
写 backtrack 函数时,需要维护走过的「路径」和当前可以做的「选择列表」,当触发「结束条件」时,将「路径」记入结果集。
其实想想看,回溯算法和动态规划是不是有点像呢?我们在动态规划系列文章中多次强调,动态规划的三个需要明确的点就是「状态」「选择」和「base case」,是不是就对应着走过的「路径」,当前的「选择列表」和「结束条件」?
某种程度上说,动态规划的暴力求解阶段就是回溯算法。只是有的问题具有重叠子问题性质,可以用 dp table 或者备忘录优化,将递归树大幅剪枝,这就变成了动态规划。而今天的两个问题,都没有重叠子问题,也就是回溯算法问题了,复杂度非常高是不可避免的。
over
⭐解题套路-回溯算法团灭子集、排列、组合问题
求子集(subset),求排列(permutation),求组合(combination)。这几个问题都可以用回溯算法解决。
一、子集
78. 子集(无重复)-中等



此时的时间复杂度呢? O(N) ? 不也是
2
N
2^N
2N ?
python代码实现;
class Solution: def subsets(self, nums: List[int]) -> List[List[int]]: # 不像之前有回溯终止条件, 或者说: 答案格式的满足条件,目前没有了。 其实和之前的代码基本一致; # 改动1: 之前使用已经访问路径标注, 不可访问的路径; 目前行不通,track里面已经包含的不走约束性不够, # 还要 排除之前已出现结果。 故每次start递增; # 改动2: 之前终止条件是: nums.size() == track.size() 现在没有这个需求, 路径上面所有节点都应该添加。 def trackBack(nums, start, track): # nums 可以选择的节点; # start: 开始搜索结果的起始范围; # track:目前递归情形下已经访问的路径 # track中的值, 不停的添加 res.append(track[:]) # 这里start是形参,所以可以变化不影响; for i in range(start, len(nums)): # 做选择 track.append(nums[i]) # 回溯 trackBack(nums, i+1, track) # 撤销选择 track.pop() res = [] track = [] trackBack(nums, 0, track) return res
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
90. 子集 II(有重复)-中等

二、组合
77. 组合-中等

- 题解


python实现:
class Solution: def combine(self, n: int, k: int) -> List[List[int]]: # 思路: 仍然是回溯算法, 排列为子集加上限定条件k def trackBack(n, start, track): if k == len(track): res.append(track[:]) return None for i in range(start, n): track.append(i) trackBack(n, i+1, track) track.pop() res = [] track = [] trackBack(n+1, 1, track) return res
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
40. 组合总和 II

216. 组合总和 III

377. 组合总和 Ⅳ

三、排列
46: 全排列-中等


46. 全排列---中等
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
示例:
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
python实现
class Solution: def permute(self, nums: List[int]) -> List[List[int]]: # 思路: 使用回溯, trackBack(), 递归判断每个叶子节点; def trackBack(nums, track): # (nums: 选择列表, track:路径) # 触发结束条件 if len(track) == len(nums): res.append(track[:]) # 传递track浅拷贝, 列表浅拷贝,内部元素不可变,则 track更新,res中append的元素不发生变化 return None # 遍历选择列表,做选择的过程, num:选择 for num in nums: # 排除不合法选择:已经在路径中元素 if num in track: continue # 做选择 track.append(num) # 进入下一层决策树 trackBack(nums, track) # 取消选择,真正回溯过程 track.pop() res = [] # 最终遍历多个路径结果 track = [] # 当前路径: 已经走过的路径 trackBack(nums, track) return res
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
四、总结

37. 解数独-困难
37. 解数独
编写一个程序,通过已填充的空格来解决数独问题。
一个数独的解法需遵循如下规则:
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
空白格用 '.' 表示。
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8


输入是一个9*9的棋盘
题解-回溯算法最佳实践:解数独
输入是一个9x9的棋盘,空白格子用点号字符 . 表示,算法需要在原地修改棋盘,将空白格子填上数字,得到一个可行解。
至于数独的要求,大家想必都很熟悉了,每行,每列以及每一个 3×3 的小方格都不能有相同的数字出现。那么,现在我们直接套回溯框架即可求解。
我们求解数独的思路很简单粗暴,就是对每一个格子所有可能的数字进行穷举。对于每个位置,应该如何穷举,有几个选择呢?很简单啊,从 1 到 9 就是选择,全部试一遍不就行了:
// 对 board[i][j] 进行穷举尝试
void backtrack(char[][] board, int i, int j) {
int m = 9, n = 9;
for (char ch = '1'; ch <= '9'; ch++) {
// 做选择
board[i][j] = ch;
// 继续穷举下一个
backtrack(board, i, j + 1);
// 撤销选择
board[i][j] = '.';
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
并不是 1 到 9 都可以取到的,有的数字不是不满足数独的合法条件吗?而且现在只是给 j 加一,那如果 j 加到最后一列了,怎么办?
很简单,当 j 到达超过每一行的最后一个索引时,转为增加 i 开始穷举下一行,并且在穷举之前添加一个判断,跳过不满足条件的数字:
void backtrack(char[][] board, int i, int j) { int m = 9, n = 9; if (j == n) { // 穷举到最后一列的话就换到下一行重新开始。 backtrack(board, i + 1, 0); return; } // 如果该位置是预设的数字,不用我们操心 if (board[i][j] != '.') { backtrack(board, i, j + 1); return; } for (char ch = '1'; ch <= '9'; ch++) { // 如果遇到不合法的数字,就跳过 if (!isValid(board, i, j, ch)) continue; board[i][j] = ch; backtrack(board, i, j + 1); board[i][j] = '.'; } } // 判断 board[i][j] 是否可以填入 n boolean isValid(char[][] board, int r, int c, char n) { for (int i = 0; i < 9; i++) { // 判断行是否存在重复 if (board[r][i] == n) return false; // 判断列是否存在重复 if (board[i][c] == n) return false; // 判断 3 x 3 方框是否存在重复 if (board[(r/3)*3 + i/3][(c/3)*3 + i%3] == n) return false; } return true; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
现在基本上差不多了,还剩最后一个问题:这个算法没有 base case,永远不会停止递归。这个好办,什么时候结束递归?显然 r == m 的时候就说明穷举完了最后一行,完成了所有的穷举,就是 base case。
前文也提到过,为了减少复杂度,我们可以让 backtrack 函数返回值为 boolean,如果找到一个可行解就返回 true,这样就可以阻止后续的递归。只找一个可行解,也是题目的本意。
最终代码修改如下:
boolean backtrack(char[][] board, int i, int j) { int m = 9, n = 9; if (j == n) { // 穷举到最后一列的话就换到下一行重新开始。 return backtrack(board, i + 1, 0); } if (i == m) { // 找到一个可行解,触发 base case return true; } if (board[i][j] != '.') { // 如果有预设数字,不用我们穷举 return backtrack(board, i, j + 1); } for (char ch = '1'; ch <= '9'; ch++) { // 如果遇到不合法的数字,就跳过 if (!isValid(board, i, j, ch)) continue; board[i][j] = ch; // 如果找到一个可行解,立即结束 if (backtrack(board, i, j + 1)) { return true; } board[i][j] = '.'; } // 穷举完 1~9,依然没有找到可行解,此路不通 return false; } boolean isValid(char[][] board, int r, int c, char n) { // 见上文 }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
现在可以回答一下之前的问题,为什么有时候算法执行的次数多,有时候少?为什么对于计算机而言,确定的数字越少,反而算出答案的速度越快?
已经实现了一遍算法,掌握了其原理,回溯就是从 1 开始对每个格子穷举,最后只要试出一个可行解,就会立即停止后续的递归穷举。所以暴力试出答案的次数和随机生成的棋盘关系很大,这个是说不准的。
那么你可能问,既然运行次数说不准,那么这个算法的时间复杂度是多少呢?
对于这种时间复杂度的计算,我们只能给出一个最坏情况,也就是 O ( 9 M ) O(9^M) O(9M),其中 M 是棋盘中空着的格子数量。你想嘛,对每个空格子穷举 9 个数,结果就是指数级的。
这个复杂度非常高,但稍作思考就能发现,实际上我们并没有真的对每个空格都穷举 9 次,有的数字会跳过,有的数字根本就没有穷举,因为当我们找到一个可行解的时候就立即结束了,后续的递归都没有展开
这个 O(9^M) 的复杂度实际上是完全穷举,或者说是找到所有可行解的时间复杂度。
如果给定的数字越少,相当于给出的约束条件越少,对于计算机这种穷举策略来说,是更容易进行下去,而不容易走回头路进行回溯的,所以说如果仅仅找出一个可行解,这种情况下穷举的速度反而比较快。
python照着大佬的思路实现。
class Solution: def solveSudoku(self, board: List[List[str]]) -> None: """ Do not return anything, modify board in-place instead. """ chars = ['1', '2', '3', '4', '5', '6', '7', '8', '9'] rows, cols = 9, 9 # 当前选择字符的可行性判断 def isValid(board, row, col, char): for i in range(9): # 判断行是否出现重复 if board[row][i] == char: return False # 判断列是否出现重复 if board[i][col] == char: return False # 判断 3*3表格是否存在重复 # 仅仅是画横线的3*3, 并没有要求 任意3*3 if board[(row//3)*3+i//3][(col//3)*3+i%3] == char: return False return True def trackBack(board, row, col): # print(row, col, board) ''' board: list 现有棋盘描述 row: int 当前搜索位置 col: int 当前搜索位置 ''' if col == cols: # 穷举到最后一列换到下一行重新开始 return trackBack(board, row+1, 0) if row == rows: # 找到一个可行解, 出发base case, 返回True return True # 这部分和之前 for col in len(grid[0])本质一样。 只是这部分现在直接跳转了 if board[row][col] != '.': # 如果有预设数字, 不用穷举,跳过 return trackBack(board, row, col+1) for char in chars: # 遇到非法字符跳过 if not isValid(board, row, col, char): continue # 做选择 board[row][col] = char # print(board) # 如果找到一个可行解, 立即结束 if trackBack(board, row, col+1): return True # 撤销选择 board[row][col] = '.' return False trackBack(board, 0, 0) # return board
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
22. 括号生成-中等
题解-回溯算法最佳实践:括号生成
括号问题可以简单分成两类,一类是前文写过的 括号的合法性判断 ,一类是合法括号的生成。对于括号合法性的判断,主要是借助「栈」这种数据结构,而对于括号的生成,一般都要利用回溯递归的思想。
括号生成算法是 LeetCode 第 22 题,要求如下:
请你写一个算法,输入是一个正整数 n,输出是 n 对儿括号的所有合法组合,函数签名如下:

回溯思路
明白了合法括号的性质,如何把这道题和回溯算法扯上关系呢?
算法输入一个整数 n,让你计算 n 对儿括号能组成几种合法的括号组合,可以改写成如下问题:
现在有 2n 个位置,每个位置可以放置字符 左括号: ( 或者 右括号: ),组成的所有括号组合中,有多少个是合法的?
这个命题和题目的意思完全是一样的对吧,那么我们先想想如何得到全部 2^(2n) 种组合,然后再根据我们刚才总结出的合法括号组合的性质筛选出合法的组合,不就完事儿了?
如何得到所有的组合呢?这就是标准的暴力穷举回溯框架啊,我们前文 回溯算法套路框架详解 都总结过了:
result = []
def backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
那么对于我们的需求,如何打印所有括号组合呢?套一下框架就出来了,伪码如下:
void backtrack(int n, int i, string& track) { // i 代表当前的位置,共 2n 个位置 // 穷举到最后一个位置了,得到一个长度为 2n 组合 if (i == 2 * n) { print(track); return; } // 对于每个位置可以是左括号或者右括号两种选择 for choice in ['(', ')'] { track.push(choice); // 做选择 // 穷举下一个位置 backtrack(n, i + 1, track); track.pop(choice); // 撤销选择 } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16

那么,现在能够打印所有括号组合了,如何从它们中筛选出合法的括号组合呢?很简单,加几个条件进行「剪枝」就行了。
对于 2n 个位置,必然有 n 个左括号,n 个右括号,所以我们不是简单的记录穷举位置 i,而是用 left 记录还可以使用多少个左括号,用 right 记录还可以使用多少个右括号,这样就可以通过刚才总结的合法括号规律进行筛选了:
vector<string> generateParenthesis(int n) { if (n == 0) return {}; // 记录所有合法的括号组合 vector<string> res; // 回溯过程中的路径 string track; // 可用的左括号和右括号数量初始化为 n backtrack(n, n, track, res); return res; } // 可用的左括号数量为 left 个,可用的右括号数量为 rgiht 个 void backtrack(int left, int right, string& track, vector<string>& res) { // 若左括号剩下的多,说明不合法 if (right < left) return; // 数量小于 0 肯定是不合法的 if (left < 0 || right < 0) return; // 当所有括号都恰好用完时,得到一个合法的括号组合 if (left == 0 && right == 0) { res.push_back(track); return; } // 尝试放一个左括号 track.push_back('('); // 选择 backtrack(left - 1, right, track, res); track.pop_back(); // 撤消选择 // 尝试放一个右括号 track.push_back(')'); // 选择 backtrack(left, right - 1, track, res); track.pop_back(); ;// 撤消选择 }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
这样,我们的算法就完成了,算法的复杂度是多少呢?这个比较难分析,对于递归相关的算法,时间复杂度这样计算(递归次数)*(递归函数本身的时间复杂度)。
backtrack 就是我们的递归函数,其中**没有任何 for 循环代码,所以递归函数本身的时间复杂度是 O(1),**但关键是这个函数的递归次数是多少?换句话说,给定一个 n,backtrack 函数递归被调用了多少次?
我们前面怎么分析动态规划算法的递归次数的?主要是看「状态」的个数对吧。其实回溯算法和动态规划的本质都是穷举,只不过动态规划存在「重叠子问题」可以优化,而回溯算法不存在而已。
所以说这里也可以用「状态」这个概念,对于 backtrack 函数,状态有三个,分别是 left, right, track,这三个变量的所有组合个数就是 backtrack 函数的状态个数(调用次数)。
left 和 right 的组合好办,他俩取值就是 0~n 嘛,组合起来也就 N 2 N^2 N2 种而已;这个 track 的长度虽然取在 0~2n,但对于每一个长度,它还有指数级的括号组合,这个是不好算的。
说了这么多,就是想让大家知道这个算法的复杂度是指数级,而且不好算,这里就不具体展开了,是 4 n n \frac{4^{n}}{\sqrt{n}} n 4n,有兴趣的读者可以搜索一下「卡特兰数」相关的知识了解一下这个复杂度是怎么算的。 (复杂度计算还不会)
题目描述:
22. 括号生成
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
示例:
输入:n = 3
输出:[
"((()))",
"(()())",
"(())()",
"()(())",
"()()()"
]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
python照着大佬代码实现:
class Solution: def generateParenthesis(self, n: int) -> List[str]: # 转换为: 总共有2n位置, 然后使用左括号、右括号进行填充的问题; # 采样暴力枚举的方式,类似于 全排列数目的计算一致。 然后使用 括号合法性的性质进行剪枝,加速计算即可; # 1、一个「合法」括号组合的左括号数量一定等于右括号数量,这个很好理解。 # 2、对于一个「合法」的括号字符串组合 p,必然对于任何 0 <= i < len(p) 都有:子串 p[0..i] 中左括号的数量都大于或等于右括号的数量。 res = [] # 最终返回结果 track = [] # 括号组合路径结果 # 回溯过程 def trackBack(left, right): ''' left: 当前情况下: 左括号剩余数量; right: 当前情况下: 右括号剩余数量; ''' # 剪枝进行加速: 对于非法操作进行终止,然后程序继续执行; # 必要条件1: 剩余左括号数量 > 右括号数量 if left > right: return # 必要条件: 剩余数量都必须大于0 if left < 0 or right < 0: return # 满足最终生成括号的合法条件 if left == right == 0: res.append(''.join(track)) return # 对于当前位置的选择进行枚举判断 # 尝试放一个左括号 # 进行选择 track.append('(') # 进入下一层决策 trackBack(left-1, right) # 左括号取出, 进行回溯 track.pop() # 尝试放一个右括号 # 进行选择 track.append(')') # 进入一下一层决策 trackBack(left, right-1) # 右括号取出, 进行回溯 track.pop() trackBack(n, n) return res
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
491. 输出所有递增子序列

- python实现:
class Solution: def findSubsequences(self, nums: List[int]) -> List[List[int]]: if not nums: return [] # n log n def trackBack(nums, start, track): # nums: 可以选择的节点 # start: 开始搜索结果的起始范围; # track: 已经访问的路径 if len(track) >= 2 and track not in res: res.append(track[:]) for i in range(start, len(nums)): if len(track) > 0 and nums[i] < track[-1]: continue # 做选择 track.append(nums[i]) # 进入下一个值进行递归 trackBack(nums, i+1, track) # 回溯 track.pop() res = [] track = [] trackBack(nums, 0, track) return res
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
140. 单词拆分 II-困难

题解-动态规划+回溯 求解具体值
思路差不多如下图: 最终返回结果;

class Solution: def wordBreak(self, s: str, wordDict: List[str]) -> List[str]: # 思路: 先使用类似于139思路判断是不是可切分,如果可节分进一步进行回溯查找; # 回溯思路: 结尾到 进行回溯(标准回溯模板); def dfs(s, end, wordSet, res, path, dp): # 如果不用拆分,整个单词就在 wordSet中,直接加入 res, 但是没有return, 仍然要递归; if s[:end+1] in wordSet: path.append(s[:end+1]) res.append(' '.join(path[::-1])) path.pop() for i in range(end): if dp[i]: suffix = s[i+1:end+1] if suffix in wordSet: path.append(suffix) dfs(s, i, wordSet, res, path, dp) path.pop() wordSet = {word for word in wordDict} sLen = len(s) dp = [False for _ in range(sLen)] for i in range(sLen): # 至关重要: 初始化操作; if s[:i+1] in wordSet: dp[i] = True continue for j in range(i): if dp[j] and s[j+1:i+1] in wordSet: dp[i] = True break res = [] # 如果有解, 才有必要回溯; if dp[-1]: path = [] dfs(s, sLen-1, wordSet, res, path, dp) return res
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
174. 地下城游戏-hard

解题思路 划分网格,网格中的值即为最终要优化的目标:骑士的健康点数; 最后一行只能往左回溯,最后一列只能往上回溯,需要特殊处理; 逆序计算到达每个房间时骑士所需的最少健康点数,最后起点即为答案; class Solution: def calculateMinimumHP(self, dungeon: List[List[int]]) -> int: # 思路: 题目关键字: 最低初始健康点数---> 动态规划; 坐标型; # 最低健康点数其实就是: 路径和最小,也就是代价最小; 但是必须保证每次都活下来; # 动态规划转移方程的推倒过程: ???? # dp[i][j]: 代表从 位置右下角到位置(i, j)时候i,j 在保证 到右下角 最小的情况下的最大值; rows = len(dungeon) cols = len(dungeon[0]) dp = [[0] * cols for _ in range(rows)] dp[-1][-1] = max(1, 1 - dungeon[-1][-1]) # 最后一列 for i in range(rows-2, -1, -1): dp[i][-1] = max(1, dp[i+1][-1] - dungeon[i][-1]) # 最右一列数据 for j in range(cols-2, -1, -1): dp[-1][j] = max(1, dp[-1][j+1] - dungeon[-1][j]) for i in range(rows-2, -1, -1): for j in range(cols-2, -1, -1): dp[i][j] = max(1, min(dp[i+1][j], dp[i][j+1]) - dungeon[i][j]) return dp[0][0]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
131. 分割回文串

题解-回溯、优化(使用动态规划预处理数组)


- 完全回溯实现
- 时间复杂度: O ( N 3 ) O(N^3) O(N3)
class Solution: def partition(self, s: str) -> List[List[str]]: # 判断字符串是不是回文串; # 双指针思想遍历; 最差时间复杂度: O(N) def check_is_palindrome(left, right): while left < right: if s[left] != s[right]: return False left = left + 1 right = right - 1 return True # 回溯操作: 递归判断符合要求的路径/选择 def dfs(start, path): if start == length: res.append(path[:]) for i in range(start, length): if not check_is_palindrome(start, i): continue # 做选择 path.append(s[start:i + 1]) # 切完第一个字符, 进一步递归; dfs(i + 1, path) # 插销选择,回溯; path.pop() res = [] length = len(s) if length == 0: return res path = [] dfs(0, path) return res
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 回溯+动态规划
- 时间复杂度: O ( N 2 ) O(N^2) O(N2)
- 空间复杂度: O ( N 2 ) O(N^2) O(N2)
class Solution: def partition(self, s: str) -> List[List[str]]: # 判断字符串是不是回文串; # 时间复杂度:O(N^2) def longestPalindrome(s): # 动态规划: dp[i][j] : 从位置i 到 j是否是回文串 size = len(s) if size < 2: return s # 初始化二维数组: dp[i][j]:字符串i-j 是否是回文串 dp = [[False]*size for _ in range(size)] # 初始条件设置 for i in range(size): dp[i][i] = True maxLen, start = 1, 0 # 遍历判断、填表: 状态、选择 # 考虑遍历顺序: 从上到下, 从左往右 for j in range(1, size): for i in range(j): if s[i] == s[j]: # 这部分自己肯定想不到的 # 例子: cbba 初始化时候: 左下方初始化值设置为: False,会判断错误 if j - i < 3: dp[i][j] = True else: dp[i][j] = dp[i+1][j-1] else: dp[i][j] = False return dp # 回溯操作: 递归判断符合要求的路径/选择 def dfs(start, path): if start == length: res.append(path[:]) for i in range(start, length): print(start, i, dp[start][i]) if not dp[start][i]: continue # 做选择 path.append(s[start:i + 1]) # 切完第一个字符, 进一步递归; dfs(i + 1, path) # 插销选择,回溯; path.pop() res = [] length = len(s) if length == 0: return res path = [] dp = longestPalindrome(s) dfs(0, path) return res
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61



