我家自动化

这个屌丝很懒，什么也没留下！

热门标签

MATLAB数据矩阵单位化，归一化，标准化_矩阵归一化

作者：我家自动化 | 2024-02-18 06:09:06

踩

矩阵归一化

1.数据矩阵单位化

单位化就是令列向量的模为1

方法一：

%%矩阵的列向量单位化
%输出矩阵Y为单位化矩阵
%方法即是矩阵中所有元素除以该元素所在列向量的二范数
clc;
clear;
X=[790 3977 849 1294 1927 1105 204 1329
    768 5037 1135 1330 1925 1459 275 1487
    942 2793 820 814 1617 942 155 976
    916 2798 901 932 1599 910 182 1135
    1006 2864 1052 1005 1618 839 196 1081];
%方法一
[m,n]=size(X);
for i=1:n
    A(1,i)=norm(X(:,i));
end
A=repmat(A,m,1);
Y=X./A;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

输出结果：

Y =
0.3974 0.4932 0.3959 0.5290 0.4941 0.4601 0.4422 0.4890
0.3863 0.6247 0.5292 0.5437 0.4936 0.6074 0.5961 0.5471
0.4738 0.3464 0.3823 0.3327 0.4146 0.3922 0.3360 0.3591
0.4608 0.3470 0.4201 0.3810 0.4100 0.3789 0.3945 0.4176
0.5060 0.3552 0.4905 0.4108 0.4149 0.3493 0.4249 0.3977

方法二：

%%矩阵的列向量单位化
%输出矩阵Y为单位化矩阵
%方法即是矩阵中所有元素除以该元素所在列向量的二范数
clc;
clear;
X=[790 3977 849 1294 1927 1105 204 1329
    768 5037 1135 1330 1925 1459 275 1487
    942 2793 820 814 1617 942 155 976
    916 2798 901 932 1599 910 182 1135
    1006 2864 1052 1005 1618 839 196 1081];
%方法二
[m,n]=size(X);
a=0;
for j=1:n
    for i=1:m
        a=a+X(i,j)^2;
    end
    A(1,j)=sqrt(a);
    a=0;
end
A=repmat(A,m,1);
Y=X./A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

输出结果：

2.数据矩阵归一化

归一化，将不同样本的同一维度的数据归一化。矩阵归一化,说白了就是整体地乘一个系数,使矩阵的绝对值=1

函数：mapminmax

默认规范范围（-1,1）

若想将规范范围划为（0,1），可编写Y=mapminmax(A,0,1);

此函数规整行向量中最大最小值，如果运用此函数，则A矩阵每一行为一个维度，每一列是一个样本。

%%矩阵数据归一化
%归一化作用是处理奇异样本矩阵
%将矩阵数据规范与一个范围之中，使不同维度具有可比性
clc;
clear;
X=[790 3977 849 1294 1927 1105 204 1329
    768 5037 1135 1330 1925 1459 275 1487
    942 2793 820 814 1617 942 155 976
    916 2798 901 932 1599 910 182 1135
    1006 2864 1052 1005 1618 839 196 1081];
Y=mapminmax(X,0,1);1
2
3
4
5
6
7
8
9
10

输出结果：

Y =
0.1553 1.0000 0.1710 0.2889 0.4567 0.2388 0 0.2982
0.1035 1.0000 0.1806 0.2215 0.3465 0.2486 0 0.2545
0.2983 1.0000 0.2521 0.2498 0.5542 0.2983 0 0.3112
0.2806 1.0000 0.2748 0.2867 0.5417 0.2783 0 0.3643
0.3036 1.0000 0.3208 0.3032 0.5330 0.2410 0 0.3317

规范范围为（-1,1）

%%矩阵数据归一化
%归一化作用是处理奇异样本矩阵
%将矩阵数据规范与一个范围之中，使不同维度具有可比性
clc;
clear;
X=[790 3977 849 1294 1927 1105 204 1329
    768 5037 1135 1330 1925 1459 275 1487
    942 2793 820 814 1617 942 155 976
    916 2798 901 932 1599 910 182 1135
    1006 2864 1052 1005 1618 839 196 1081];
Y=mapminmax(X);1
2
3
4
5
6
7
8
9
10

输出结果：

Y =
-0.6894 1.0000 -0.6581 -0.4222 -0.0867 -0.5224 -1.0000 -0.4037
-0.7929 1.0000 -0.6388 -0.5569 -0.3070 -0.5027 -1.0000 -0.4910
-0.4033 1.0000 -0.4958 -0.5004 0.1084 -0.4033 -1.0000 -0.3776
-0.4388 1.0000 -0.4503 -0.4266 0.0833 -0.4434 -1.0000 -0.2714
-0.3928 1.0000 -0.3583 -0.3936 0.0660 -0.5180 -1.0000 -0.3366

3.数据矩阵标准化

让矩阵每一列内积为1,不同列内积为0。标准化的数据均值为0，标准差为1

标准化函数zscore(x)

就是原数据减去均值，再除以标准差（无偏估计）

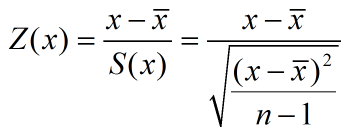
即Z=(x-mean(x))./std(x);

%%矩阵数据标准化
clc;
clear;
X=[790 3977 849 1294 1927 1105 204 1329
    768 5037 1135 1330 1925 1459 275 1487
    942 2793 820 814 1617 942 155 976
    916 2798 901 932 1599 910 182 1135
    1006 2864 1052 1005 1618 839 196 1081];
Y=zscore(X);1
2
3
4
5
6
7
8

输出结果：

Y =
-0.9261 0.4840 -0.7522 0.9640 1.1002 0.2177 0.0358 0.6225
-1.1419 1.5457 1.3487 1.1224 1.0886 1.6449 1.6257 1.3944
0.5651 -0.7020 -0.9653 -1.1488 -0.6967 -0.4395 -1.0614 -1.1023
0.3100 -0.6969 -0.3702 -0.6294 -0.8011 -0.5685 -0.4568 -0.3254
1.1929 -0.6308 0.7390 -0.3081 -0.6909 -0.8547 -0.1433 -0.5892

也可以按照上面的公式：

%%矩阵数据标准化
clc;
clear;
X=[790 3977 849 1294 1927 1105 204 1329
    768 5037 1135 1330 1925 1459 275 1487
    942 2793 820 814 1617 942 155 976
    916 2798 901 932 1599 910 182 1135
    1006 2864 1052 1005 1618 839 196 1081];
1
2
3
4
5
6
7
8

Y=(X-repmat(mean(X),5,1))./repmat(std(X),5,1);输出结果：

1.数据矩阵单位化

方法一：

%%矩阵的列向量单位化
%输出矩阵Y为单位化矩阵
%方法即是矩阵中所有元素除以该元素所在列向量的二范数
clc;
clear;
X=[790 3977 849 1294 1927 1105 204 1329
    768 5037 1135 1330 1925 1459 275 1487
    942 2793 820 814 1617 942 155 976
    916 2798 901 932 1599 910 182 1135
    1006 2864 1052 1005 1618 839 196 1081];
%方法一
[m,n]=size(X);
for i=1:n
    A(1,i)=norm(X(:,i));
end
A=repmat(A,m,1);
Y=X./A;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

输出结果：

方法二：

%%矩阵的列向量单位化
%输出矩阵Y为单位化矩阵
%方法即是矩阵中所有元素除以该元素所在列向量的二范数
clc;
clear;
X=[790 3977 849 1294 1927 1105 204 1329
    768 5037 1135 1330 1925 1459 275 1487
    942 2793 820 814 1617 942 155 976
    916 2798 901 932 1599 910 182 1135
    1006 2864 1052 1005 1618 839 196 1081];
%方法二
[m,n]=size(X);
a=0;
for j=1:n
    for i=1:m
        a=a+X(i,j)^2;
    end
    A(1,j)=sqrt(a);
    a=0;
end
A=repmat(A,m,1);
Y=X./A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

输出结果：

2.数据矩阵归一化

归一化，将不同样本的同一维度的数据归一化。

函数：mapminmax

默认规范范围（-1,1）

若想将规范范围划为（0,1），可编写Y=mapminmax(A,0,1);

此函数规整行向量中最大最小值，如果运用此函数，则A矩阵每一行为一个维度，每一列是一个样本。

%%矩阵数据归一化
%归一化作用是处理奇异样本矩阵
%将矩阵数据规范与一个范围之中，使不同维度具有可比性
clc;
clear;
X=[790 3977 849 1294 1927 1105 204 1329
    768 5037 1135 1330 1925 1459 275 1487
    942 2793 820 814 1617 942 155 976
    916 2798 901 932 1599 910 182 1135
    1006 2864 1052 1005 1618 839 196 1081];
Y=mapminmax(X,0,1);1
2
3
4
5
6
7
8
9
10

输出结果：

规范范围为（-1,1）

%%矩阵数据归一化
%归一化作用是处理奇异样本矩阵
%将矩阵数据规范与一个范围之中，使不同维度具有可比性
clc;
clear;
X=[790 3977 849 1294 1927 1105 204 1329
    768 5037 1135 1330 1925 1459 275 1487
    942 2793 820 814 1617 942 155 976
    916 2798 901 932 1599 910 182 1135
    1006 2864 1052 1005 1618 839 196 1081];
Y=mapminmax(X);1
2
3
4
5
6
7
8
9
10

输出结果：

3.数据矩阵标准化

标准化的数据均值为0，标准差为1

标准化函数zscore(x)

就是原数据减去均值，再除以标准差（无偏估计）

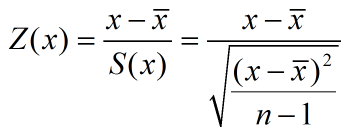
即Z=(x-mean(x))./std(x);

%%矩阵数据标准化
clc;
clear;
X=[790 3977 849 1294 1927 1105 204 1329
    768 5037 1135 1330 1925 1459 275 1487
    942 2793 820 814 1617 942 155 976
    916 2798 901 932 1599 910 182 1135
    1006 2864 1052 1005 1618 839 196 1081];
Y=zscore(X);1
2
3
4
5
6
7
8

输出结果：

也可以按照上面的公式：

%%矩阵数据标准化
clc;
clear;
X=[790 3977 849 1294 1927 1105 204 1329
    768 5037 1135 1330 1925 1459 275 1487
    942 2793 820 814 1617 942 155 976
    916 2798 901 932 1599 910 182 1135
    1006 2864 1052 1005 1618 839 196 1081];
1
2
3
4
5
6
7
8

Y=(X-repmat(mean(X),5,1))./repmat(std(X),5,1);输出结果：

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/我家自动化/article/detail/105510