主成分分析法(PCA)及其python实现_python pca

主成分分析法（Principal Component Analysis，PCA）是一种用于把高维数据降成低维，使分析变得更加简便的分析方法。比如我们的一个样本可以由$n$维随机变量$(X_1,X_2,...,X_n)$来刻画，运用主成分分析法，我们可以把这些分量用更少的、这$n$个分量的线性组合来表示。本文多为学习后的个人理解，如有错误还请指出。

基本思想

我们把降维后的变量称为主成分（Principal Component），设其为$Z_1,Z_2,...,Z_n$（我们并不取这全部的$n$个变量，否则降维就没有意义了）。$Z_i$称为第$i$主成分。每个主成分都是原来$n$个变量的线性组合，即
{ Z 1 = a 11 X 1 + a 12 X 2 + . . . + a 1 n X n Z 2 = a 21 X 1 + a 22 X 2 + . . . + a 2 n X n . . . Z n = a n 1 X 1 + a n 2 X 2 + . . . + a n n X n

$$\begin{cases}Z_1=a_{11}X_1+a_{12}X_2+...+a_{1n}X_n\\ Z_2=a_{21}X_1+a_{22}X_2+...+a_{2n}X_n \\ ...\\Z_n=a_{n1}X_1+a_{n2}X_2+...+a_{nn}X_n \\ \end{cases}$$ ⎩ ⎨ ⎧​Z1​=a11​X1​+a12​X2​+...+a1n​Xn​Z2​=a21​X1​+a22​X2​+...+a2n​Xn​...Zn​=an1​X1​+an2​X2​+...+ann​Xn​​
或者写成更简便的线性代数形式：设$Z=\left(\begin{array}{c}{Z}_1\\ Z_2\\ ⋮\\ Z_n\end{array}\right),X=\left(\begin{array}{c}{X}_1\\ X_2\\ ⋮\\ X_n\end{array}\right),A=\left(\begin{array}{ccc}{a}_{11}& \cdots & a_{1n}\\ ⋮& \ddots & ⋮\\ a_{n1}& \cdots & a_{nn}\end{array}\right),$则这个关系可被表示为$Z=AX.$
为了达到降维的目的，我们需要保证

$(1)Z_1,Z_2,...,Z_n$是线性无关的，这要求$A$是正交阵。
如果存在线性相关的关系（$\exists$ 不全为$0$的$k_1,k_2,...,k_n$使得$k_1{Z}_1+k_2{Z}_2+...+k_n{Z}_n=0$），我们得到的结果中就存在着冗余信息(某个主成分可以由其它主成分表示)，这种情况应该被排除。

$(2)$选出$n$个主成分中能显著代表原本变量的$k(k<n)$个，来实现对数据的降维。
这一条提出了一个问题：我们按照什么标准来衡量主成分的好坏关系呢？统计学认为，一组数据越分散，它的方差越大，它所包含的信息就越多。（知乎的这个问题讨论了这一点）因此，PCA选出这$n$个主成分中方差最大的$k$个作为新的变量。

数学推导

设我们的$m$个样本对应的数据矩阵为 R = ( r 11 ⋯ r 1 m ⋮ ⋱ ⋮ r n 1 ⋯ r n m ) R=

$$\begin{pmatrix}r_{11} & \cdots & r_{1m}\\ \vdots & \ddots & \vdots \\ r_{n1} & \cdots & r_{nm}\end{pmatrix}$$ R=⎝ ⎛​r11​⋮rn1​​⋯⋱⋯​r1m​⋮rnm​​⎠ ⎞​,每列代表一个样本；我们先将其标准化，使每行的均值为$0$，并消除量纲的影响，便于进一步处理：

$x_{ij}=(r_{ij}-\overline{r_i})/s_i,$

其中$\overline{r_i}$和$s_i$分别为第$i$行的均值和样本标准差，记处理后的矩阵为$X=(x_{ij}{)}_{n\times m};$对该矩阵做线性变换的结果为$F=AX=(z_{ij}{)}_{n\times m}.$

我们用$D(Z)$表示$n$维随机变量 Z = ( Z 1 Z 2 ⋮ Z n ) Z=

$$\begin{pmatrix}Z_1\\Z_2\\ \vdots \\Z_n\end{pmatrix}$$ Z=⎝ ⎛​Z1​Z2​⋮Zn​​⎠ ⎞​的协方差矩阵，那么有

D ( Z ) = ( C o v ( Z 1 , Z 1 ) ⋯ C o v ( Z 1 , Z n ) ⋮ ⋱ ⋮ C o v ( Z n , Z 1 ) ⋯ C o v ( Z n , Z n ) ) D(Z)=

$$\begin{pmatrix} Cov(Z_1,Z_1) & \cdots & Cov(Z_1,Z_n)\\ \vdots & \ddots & \vdots \\ Cov(Z_n,Z_1) & \cdots & Cov(Z_n,Z_n)\end{pmatrix}$$ D(Z)=⎝ ⎛​Cov(Z1​,Z1​)⋮Cov(Zn​,Z1​)​⋯⋱⋯​Cov(Z1​,Zn​)⋮Cov(Zn​,Zn​)​⎠ ⎞​

由上一部分的条件$(1)$，应当有$Z_i,Z_j(i\ne j)$线性不相关，即$Cov(Z_i,Z_j)=0$.而$Cov(Z_i,Z_i)=D(Z_i)$,即$Z_i$的方差（注意跟上文的$D(Z)$的记号意义不同，上面的$D$指的是协方差矩阵），因此$D(Z_i)$就是一个对角矩阵，即

D ( Z ) = ( D ( Z 1 ) D ( Z 2 ) ⋱ D ( Z n ) ) D(Z)=

$$\begin{pmatrix}D(Z_1) & & \\ & D(Z_2) & \\ & & \ddots & \\ & & & D(Z_n)\end{pmatrix}$$ D(Z)=⎝ ⎛​D(Z1​)​D(Z2​)​⋱​D(Zn​)​⎠ ⎞​

由协方差的定义，$Cov(Z_i,Z_j)=E(Z_i{Z}_j)-E(Z_i)E(Z_j);$

由于$X$经我们处理，对任意的$X_i$都有$E(X_i)=0$,故$E(Z_i)=E(a_{i1}{X}_1+...+a_{in}{X}_n)=0,$

$Cov(Z_i,Z_j)=E(Z_i{Z}_j)=\frac{1}{m}\sum _{t=1}^m{z}_{it}{z}_{jt}.$那么上面的$D(Z)$还可表示为

D ( Z ) = ( C o v ( Z 1 , Z 1 ) ⋯ C o v ( Z 1 , Z n ) ⋮ ⋱ ⋮ C o v ( Z n , Z 1 ) ⋯ C o v ( Z n , Z n ) ) = ( D ( Z 1 ) D ( Z 2 ) ⋱ D ( Z n ) ) = 1 m F F T . D(Z)=

$$\begin{pmatrix} Cov(Z_1,Z_1) & \cdots & Cov(Z_1,Z_n)\\ \vdots & \ddots & \vdots \\ Cov(Z_n,Z_1) & \cdots & Cov(Z_n,Z_n)\end{pmatrix}$$ = $$\begin{pmatrix}D(Z_1) & & \\ & D(Z_2) & \\ & & \ddots & \\ & & & D(Z_n)\end{pmatrix}$$ =\frac{1}{m}FF^T. D(Z)=⎝ ⎛​Cov(Z1​,Z1​)⋮Cov(Zn​,Z1​)​⋯⋱⋯​Cov(Z1​,Zn​)⋮Cov(Zn​,Zn​)​⎠ ⎞​=⎝ ⎛​D(Z1​)​D(Z2​)​⋱​D(Zn​)​⎠ ⎞​=m1​FFT.

又因为$F=AX,D(Z)=\frac{1}{m}(AX)(AX{)}^T=\frac{1}{m}(AX)(X^T{A}^T)=A(\frac{1}{m}X{X}^T)A^T=AD(X)A^T$，这里$D(X)$表示$n$维随机变量 ( X 1 X 2 ⋮ X n )

$$\begin{pmatrix}X_1\\X_2\\ \vdots \\X_n\end{pmatrix}$$ ⎝ ⎛​X1​X2​⋮Xn​​⎠ ⎞​的协方差矩阵。

由于$D(X)$是实对称矩阵（这一点由协方差矩阵的定义即得：$Cov(X_i,X_j)=Cov(X_j,X_i)$），由实对称矩阵的性质，$D(X)$一定可以相似对角化，即存在正交矩阵$P,$使得

P T D ( X ) P = ( λ 1 λ 2 ⋱ λ n ) ( 1 ) P^TD(X)P=

$$\begin{pmatrix}\lambda_1 & & & \\ & \lambda_2 & & \\ & & \ddots & \\ & & & \lambda_n\end{pmatrix}$$ \hspace{4.5cm}(1) PTD(X)P=⎝ ⎛​λ1​​λ2​​⋱​λn​​⎠ ⎞​(1)

其中${\lambda }_1...{\lambda }_n$为$D(X)$的$n$个特征值。

这时候我们取出上面得到的式子

D ( Z ) = ( D ( Z 1 ) D ( Z 2 ) ⋱ D ( Z n ) ) = A D ( X ) A T ( 2 ) D(Z)=

$$\begin{pmatrix}D(Z_1) & & \\ & D(Z_2) & \\ & & \ddots & \\ & & & D(Z_n)\end{pmatrix}$$ =AD(X)A^T\hspace{1.5cm}(2) D(Z)=⎝ ⎛​D(Z1​)​D(Z2​)​⋱​D(Zn​)​⎠ ⎞​=AD(X)AT(2)

由基本思想部分的前提，$A$应当是正交矩阵，于是我们得到 ( D ( Z 1 ) D ( Z 2 ) ⋱ D ( Z n ) ) ∼ D ( X ) .

$$\begin{pmatrix}D(Z_1) & & \\ & D(Z_2) & \\ & & \ddots & \\ & & & D(Z_n)\end{pmatrix}$$ \sim D(X). ⎝ ⎛​D(Z1​)​D(Z2​)​⋱​D(Zn​)​⎠ ⎞​∼D(X).

由线性代数定理（若$n$阶方阵$A$与对角矩阵$D$相似，则$D$对角线上的元素即为$A$的$n$个特征值），${\lambda }_1...{\lambda }_n$即$D(Z_1)...D(Z_n).$更巧妙的是，我们可以求得变换矩阵$A=P^T$,即将$D(X)$相似对角化所需的正交阵之转置。得到了这个变换矩阵，我们就能得到$n$个变换后的主成分了。具体地说，若

A = P T = ( a 11 ⋯ a 1 n ⋮ ⋱ ⋮ a n 1 ⋯ a n n ) , A=P^T=

$$\begin{pmatrix}a_{11} & \cdots & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{n1} & \cdots & a_{nn}\end{pmatrix}$$ , A=PT=⎝ ⎛​a11​⋮an1​​⋯⋱⋯​a1n​⋮ann​​⎠ ⎞​,
则第$i$个主成分$Z_i=a_{i1}{X}_1+a_{i2}{X}_2+...+a_{in}{X}_n:$$X_i$前面的系数即$A$的第$i$行，$P$的第$i$列，正好是$D(X)$的第$i$个特征值对应的特征向量（指的是相似对角化矩阵$P$中标准的特征向量）。

推导结论

经过上面一大串推导，我们得到如下结论：

若$X$是标准化处理过的数据矩阵，那么$D(X)$的$n$个特征值${\lambda }_1,{\lambda }_2,...,{\lambda }_n$即为线性变换后的$n$个随机变量（即我们提到的主成分）$Z_1,Z_2,...,Z_n$的方差$D(Z_1),D(Z_2),...,D(Z_n)$；线性变换所需矩阵$A=P^T$,其中$P$为将$D(X)$相似对角化所需的正交阵(由线性代数知识，这也是$D(X)$的$n$个特征向量组成的矩阵)。

这个结论使我们能够求出线性变换所需要的矩阵$A$;此外我们可以根据特征值将$n$个主成分排序，求得方差最大的$k$个主成分。更具体地，求排序后的$n$个主成分的算法如下：

$1.将原始数据矩阵R标准化:x_{ij}=(r_{ij}-\overline{r_i})/s_i,得到矩阵X;$
$2.求X的协方差矩阵D(X);$
$3.求D(X)的特征值{\lambda }_1...{\lambda }_n和将其相似对角化需要的正交矩阵P;$
$4.方差第i大的主成分系数即第i大特征值对应的（单位化了的）特征向量.$

举个例子：（数据来自https://zhuanlan.zhihu.com/p/454447043）
我们要将如下的数据中5个变量（设能力，品格，担保，资本，环境为$X_1...X_5$）降维：

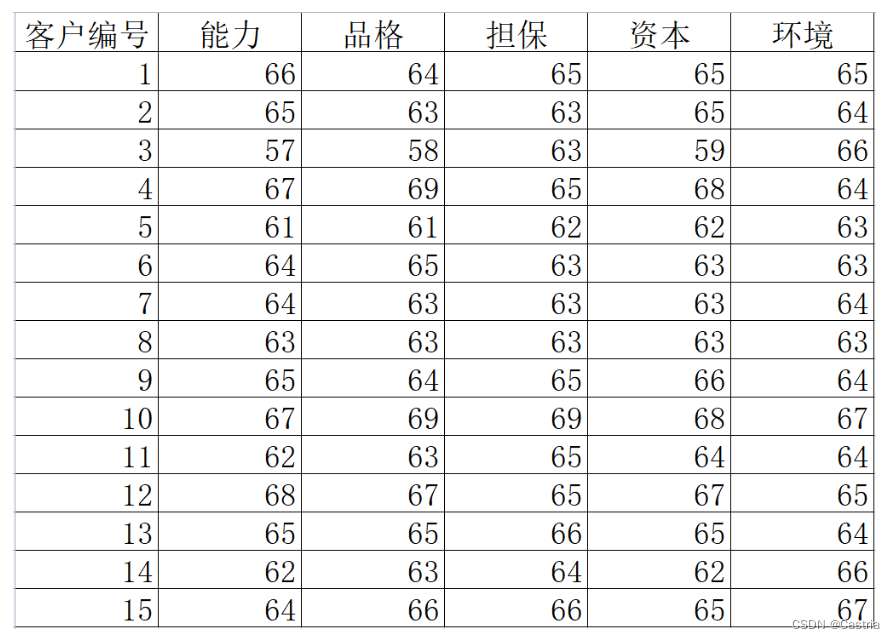
首先我们写出它对应的原始数据矩阵：
R = ( 66 65 57 ⋯ 62 64 64 63 58 ⋯ 63 66 ⋮ ⋮ 65 64 66 ⋯ 66 67 ) 5 × 15 R=

$$\begin{pmatrix}66 & 65 & 57 & \cdots & 62 & 64\\ 64 & 63 & 58 & \cdots & 63 & 66 \\ \vdots & & & & & \vdots\\ 65 & 64 & 66 & \cdots &66 & 67\end{pmatrix}$$ _{5 \times 15} R=⎝ ⎛​6664⋮65​656364​575866​⋯⋯⋯​626366​6466⋮67​⎠ ⎞​5×15​
然后将其标准化：
$X={\left(\begin{array}{ccc}0.7200823& \cdots & 0.0\\ -0.06996503& \cdots & 0.62968524\\ ⋮& & ⋮\\ 0.29580399& \cdots & 1.77482393\end{array}\right)}_{5\times 15}$
求出$X$的协方差矩阵：
$D(X)={\left(\begin{array}{cccc}1.0& \cdots & & 0.01901814\\ 0.8816601& 1.0& \cdots & 0.20695934\\ ⋮& & & ⋮\\ 0.01901814& & \cdots & 1.0\end{array}\right)}_{5\times 5}$
求出$D(X)$的特征值（从大到小排列）和特征向量：
${\lambda }_1=3.45317841{xx}_1={\left(\begin{array}{ccccc}0.48198& 0.51227& 0.45384& 0.51336& 0.18914\end{array}\right)}^T$
${\lambda }_2=1.22308928{xx}_2={\left(\begin{array}{ccccc}0.33297& 0.13247& -0.39212& 0.20476& -0.82213\end{array}\right)}^T$
${\lambda }_3=0.17872745{xx}_3={\left(\begin{array}{ccccc}0.42459& 0.1072& -0.72892& -0.05405& 0.52344\end{array}\right)}^T$
${\lambda }_4=0.09923816{xx}_4={\left(\begin{array}{ccccc}-0.39138& 0.84166& -0.11708& -0.34902& -0.05398\end{array}\right)}^T$
${\lambda }_5=0.0457667{xx}_5={\left(\begin{array}{ccccc}-0.56866& 0.01252& -0.3086& 0.75485& 0.1069\end{array}\right)}^T$

我们怎么确定最终取出几个主成分呢？一般认为当取出的$k$个主成分方差贡献比例之和达到$85\%$时就可以较好地代替原来的$n$个变量了。因此我们还需要计算每个特征值所对应的方差贡献比例。由于${\lambda }_i=D(Z_i),$特征值${\lambda }_i$的方差占比即$\frac{{\lambda }_i}{\sum _{j=1}^n{\lambda }_i}.$按照上述方法，计算方差占比如下：

特征值${\lambda }_1$的方差贡献率$0.69064$,累计方差贡献率$0.69064;$
特征值${\lambda }_2$的方差贡献率$0.24462$,累计方差贡献率$0.93525;$（已到达$85\%$）
特征值${\lambda }_3$的方差贡献率$0.03575$,累计方差贡献率$0.971;$
特征值${\lambda }_4$的方差贡献率$0.01985$,累计方差贡献率$0.99085;$
特征值${\lambda }_5$的方差贡献率$0.00915$,累计方差贡献率$\mathrm{1.0.}$

可以看到前$2$个特征值对应的主成分即达到了$85\%$的方差贡献率，因此我们可以把原来的$5$个变量“浓缩”表示为下面的$2$个主成分（系数即为特征值对应的特征向量的各分量）：

$z_1=0.48198x_1+0.51227x_2+0.45384x_3+0.51336x_4+0.18914x_5;$
$z_2=0.33297x_2+0.13247x_2-0.39212x_3+0.20476x_4-0.82213x_5.$
这样，我们就成功实现了降维，以后我们分析数据的时候就可以用$z_1$和$z_2$来代替原来的五个指标了。

python实现

下面我们用python来实现一下上述的过程。

import numpy as np
from numpy import linalg 

class PCA:

    '''
    dataset 形如array([样本1,样本2,...,样本m]),每个样本是一个n维的ndarray
    '''
    def __init__(self, dataset):
    	# 这里的参数跟上文是反着来的(每行是一个样本)，需要转置一下
        self.dataset = np.matrix(dataset, dtype='float64').T

    '''
    求主成分;
    threshold可选参数表示方差累计达到threshold后就不再取后面的特征向量.
    '''
    def principal_comps(self, threshold = 0.85):
    	# 返回满足要求的特征向量
        ret = []
        data = []

		# 标准化
        for (index, line) in enumerate(self.dataset):
            self.dataset[index] -= np.mean(line)
            # np.std(line, ddof = 1)即样本标准差(分母为n - 1)
            self.dataset[index] /= np.std(line, ddof = 1)
        # 求协方差矩阵
        Cov = np.cov(self.dataset)
		# 求特征值和特征向量
        eigs, vectors = linalg.eig(Cov)
		# 第i个特征向量是第i列，为了便于观察将其转置一下
        for i in range(len(eigs)):
            data.append((eigs[i], vectors[:, i].T))
        # 按照特征值从大到小排序
        data.sort(key = lambda x: x[0], reverse = True)

        sum = 0
        for comp in data:
            sum += comp[0] / np.sum(eigs)
            ret.append(
                tuple(map(
                	# 保留5位小数
                    lambda x: np.round(x, 5),
                    # 特征向量、方差贡献率、累计方差贡献率
                    (comp[1], comp[0] / np.sum(eigs), sum)
                ))
            )
            print('特征值:', comp[0], '特征向量:', ret[-1][0], '方差贡献率:', ret[-1][1], '累计方差贡献率:', ret[-1][2])
            if sum > threshold:
                return ret      

        return ret 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

测试一下刚才的例子：

p = PCA(
[[66, 64, 65, 65, 65],
 [65, 63, 63, 65, 64],
 [57, 58, 63, 59, 66],
 [67, 69, 65, 68, 64],
 [61, 61, 62, 62, 63],
 [64, 65, 63, 63, 63],
 [64, 63, 63, 63, 64],
 [63, 63, 63, 63, 63],
 [65, 64, 65, 66, 64],
 [67, 69, 69, 68, 67],
 [62, 63, 65, 64, 64],
 [68, 67, 65, 67, 65],
 [65, 65, 66, 65, 64],
 [62, 63, 64, 62, 66],
 [64, 66, 66, 65, 67]]
)

lst = p.principal_comps()

print(lst)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

输出结果：

# 这部分是运行时输出的
特征值: 3.4531784074578318 特征向量: [0.48198 0.51227 0.45384 0.51336 0.18914] 方差贡献率: 0.69064 累计方差贡献率: 0.69064
特征值: 1.2230892804516 特征向量: [ 0.33297  0.13247 -0.39212  0.20476 -0.82213] 方差贡献率: 0.24462 累计方差贡献率: 0.93525
# 这部分是返回的结果，为了美观稍微调整了一下格式
[
(array([0.48198, 0.51227, 0.45384, 0.51336, 0.18914]), 0.69064, 0.69064), 
(array([ 0.33297,  0.13247, -0.39212,  0.20476, -0.82213]), 0.24462, 0.93525)
]
1
2
3
4
5
6
7
8

我这里设置的返回结果是一个三元组$(特征向量,方差贡献率,累计方差贡献率)$,如果有需要也可以自己调整一下返回的结果格式。此外，通过调整threshold可选参数可以设置累计方差贡献率到达多少时停止取主成分向量（默认为0.85）。

使用sklearn的PCA模块实现

这种经典的算法sklearn库也已经帮我们实现好了。对于上面的例子，其等价的使用sklearn库的代码如下：

import numpy as np
from sklearn.decomposition import PCA

X = np.array(
[[66, 64, 65, 65, 65],
 [65, 63, 63, 65, 64],
 [57, 58, 63, 59, 66],
 [67, 69, 65, 68, 64],
 [61, 61, 62, 62, 63],
 [64, 65, 63, 63, 63],
 [64, 63, 63, 63, 64],
 [63, 63, 63, 63, 63],
 [65, 64, 65, 66, 64],
 [67, 69, 69, 68, 67],
 [62, 63, 65, 64, 64],
 [68, 67, 65, 67, 65],
 [65, 65, 66, 65, 64],
 [62, 63, 64, 62, 66],
 [64, 66, 66, 65, 67]]
)

# n_components 指明了降到几维
pca = PCA(n_components = 2)

# 利用数据训练模型（即上述得出特征向量的过程）
pca.fit(X)

# 得出原始数据的降维后的结果；也可以以新的数据作为参数，得到降维结果。
print(pca.transform(X))

# 打印各主成分的方差占比
print(pca.explained_variance_ratio_)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

运行结果：

[[-1.51394918 -0.21382815]
 [ 0.25137676 -1.8134245 ]
 [10.61577071  2.68155382]
 [-6.48520841 -1.16575919]
 [ 5.53026102 -1.52083322]
 [ 0.70154125 -1.8544697 ]
 [ 1.82460091 -1.29624147]
 [ 2.44281085 -1.60484093]
 [-1.40146605 -0.59189041]
 [-7.76925956  3.34817657]
 [ 1.8850487   0.61749314]
 [-5.41819247 -0.9163256 ]
 [-1.764172    0.155228  ]
 [ 3.06230672  1.51679123]
 [-1.96146925  2.65837042]]
# 下面是方差贡献率
[0.82399563 0.11748567]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

我们发现这个方差贡献率（也就是特征值占比）跟我们手写的很不一样。（手写的是[0.69064, 0.24462]）。这里可能会出现分歧的地方就是是否对原始数据除以样本标准差。当我把手写代码部分的

self.dataset[index] /= np.std(line, ddof = 1)
1

这一行注释掉后，发现运行结果与sklearn库的基本一致了：

特征值: 22.075235372070864 特征向量: [0.56177 0.58975 0.27868 0.50573 0.05644] 方差贡献率: 0.824 累计方差贡献率: 0.824
特征值: 3.1474971323292125 特征向量: [ 0.37826 -0.06431 -0.61334  0.06946 -0.68686] 方差贡献率: 0.11749 累计方差贡献率: 0.94148
1
2

因此可以得出sklearn库在训练时似乎没有消除量纲，即没有对数据除以其样本标准差。当然，这仅仅是个人理解，不过与sklearn库结果基本吻合大致上印证了这个猜想。在一篇文章里我找到了关于量纲的讨论：若各个变量的单位一致，则各个属性是可以比较的，此时可以直接求协方差；但当各个变量单位不同时（如身高/体重），这时不同变量之间没有可比性，这时就应该消除量纲的影响（即除以样本标准差）。

参考资料

1.https://www.cnblogs.com/Luv-GEM/p/10765574.html
2.https://www.zhihu.com/question/274997106/answer/1055696026
3.https://zhuanlan.zhihu.com/p/454447043
4.https://www.jianshu.com/p/c21c0e2c403a