2022年第十三届蓝桥杯省赛真题 (C/C++ 研究生组)_2022年蓝桥杯宁夏省赛真题

题目A:裁纸刀 （5分）

• 题目描述
  小蓝有一个裁纸刀，每次可以将一张纸沿一条直线裁成两半。
  小蓝用一张纸打印出两行三列共6个二维码，至少使用九次裁出来，下图给出了一种裁法。
  

在上面的例子中，小蓝的打印机没办法打印到边缘，所以边缘至少要裁 4次。另外，小蓝每次只能裁一张纸，不能重叠或者拼起来裁。
如果小蓝要用一张纸打印出20行22列共440个二维码，他至少需要裁多少次？

• 答案提交
  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

图中边缘必须裁四次，然后得到两行三列共六张二维码。横线5裁一次，竖线6 7 8 9各裁一次，加上裁边缘的四次，共九次。也就是说，横向裁剪次数为【行数-1】次。竖向裁剪次数为【(列数-1)行数】次。
题目共20行22列，则次数为：4 + 19 + (2120) = 443次。

试题 B：灭鼠先锋（5分）

• 问题描述
  灭鼠先锋是一个老少咸宜的棋盘小游戏，由两人参与，轮流操作。
  灭鼠先锋的棋盘有各种规格，本题中游戏在两行四列的棋盘上进行。游戏的规则为：两人轮流操作，每次可选择在棋盘的一个空位上放置一个棋子，或在同一行的连续两个空位上各放置一个棋子，放下棋子后使棋盘放满的一方输掉游戏。
  小蓝和小乔一起玩游戏，小蓝先手，小乔后手。小蓝可以放置棋子的方法很多，通过旋转和翻转可以对应如下四种情况：
  
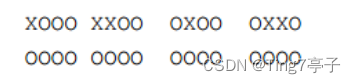
  其中 ○ 表示棋盘上的一个方格为空，x 表示该方格已经放置了棋子。请问，对于以上四种情况，如果小蓝和小乔都是按照对自己最优的策略来玩游戏，小蓝是否能获胜。如果获胜，请用 v 表示，否则用 L 表示。请将四种情况的胜负结果按顺序连接在一起提交。
• 【答案提交】
  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个长度为 4 的由大写字母v和L组成的字符串，如VVLL，在提交答案时只填写这个字符串，填写多余的内容将无法得分。

题目C:质因数个数（10分）

• 题目描述
  给定正整数 n，请问有多少个质数是 n 的约数
• 输入格式
  输入的第一行包含一个整数 n。
• 输出格式
  输出一个整数，表示 n 的质数约数个数。
• 样例输入
  396
• 样例输出
  3
• 提示
  396 有 2, 3, 11 三个质数约数。
  对于 30% 的评测用例，1 ≤ n ≤ 10000。
  对于 60% 的评测用例，1 ≤ n ≤ 10^9。
  对于所有评测用例，1 ≤ n ≤ 10^16。

评测链接： https://www.dotcpp.com/oj/problem2692.html

#include <bits/stdc++.h>
using namespace std;

int main()
{
    long n, count, s;
    cin >> n;
    count = 0;

    for (long i = 2; i * i <= n; i++)
    {
        if (n % i == 0)
            count++;
        while (n % i == 0)
            n = n / i;
    }

    if (n > 1)
        count++;
    cout << count << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

题目D:选数异或 （10分）

• 题目描述
  给定一个长度为 n 的数列 A1, A2, · · · , An 和一个非负整数 x，给定 m 次查询, 每次询问能否从某个区间 [l,r] 中选择两个数使得他们的异或等于 x 。
• 输入格式
  输入的第一行包含三个整数 n, m, x 。
  第二行包含 n 个整数 A1, A2, · · · , An 。
  接下来 m 行，每行包含两个整数 li ,ri 表示询问区间 [li ,ri ] 。
• 输出格式
  对于每个询问, 如果该区间内存在两个数的异或为 x 则输出 yes, 否则输出 no。
• 样例输入
  4 4 1
  1 2 3 4
  1 4
  1 2
  2 3
  3 3
• 样例输出
  yes
  no
  yes
  no
• 提示
  显然整个数列中只有 2, 3 的异或为 1。
  对于 20% 的评测用例，1 ≤ n, m ≤ 100；
  对于 40% 的评测用例，1 ≤ n, m ≤ 1000；
  对于所有评测用例，1 ≤ n, m ≤ 100000 ，0 ≤ x < 220 ，1 ≤ li ≤ ri ≤ n ， 0 ≤ Ai < 220。

评测链接： https://www.dotcpp.com/oj/problem2665.html

题目E:GCD （15分）

• 题目描述
  给定两个不同的正整数 a, b，求一个正整数 k 使得 gcd(a + k, b + k) 尽可能大，其中 gcd(a, b) 表示 a 和 b 的最大公约数，如果存在多个 k，请输出所有满足条件的 k 中最小的那个。
• 输入格式
  输入一行包含两个正整数 a, b，用一个空格分隔。
• 输出格式
  输出一行包含一个正整数 k。
• 样例输入
  5 7
• 样例输出
  1
• 提示
  对于 20% 的评测用例，a < b ≤ 10^5 ；
  对于 40% 的评测用例，a < b ≤ 10^9 ；
  对于所有评测用例，1 ≤ a < b ≤ 10^18 。
  评测链接： https://www.dotcpp.com/oj/problem2682.html

求最大公约数的函数：

int gcd(int a, int b) {
    if (b == 0) {
        return a;
    }
    return gcd(b, a % b);
}
1
2
3
4
5
6

题目F:爬树的甲壳虫 （15分）

• 题目描述
  有一只甲壳虫想要爬上一颗高度为 n 的树，它一开始位于树根，高度为 0，当它尝试从高度 i − 1 爬到高度为 i 的位置时有 Pi 的概率会掉回树根，求它从树根爬到树顶时，经过的时间的期望值是多少。

• 输入格式
  输入第一行包含一个整数 n 表示树的高度。
  接下来 n 行每行包含两个整数 xi , yi，用一个空格分隔，Pi=xi/yi。

• 输出格式
  输出一行包含一个整数表示答案，答案是一个有理数，请输出答案对质数 998244353 取模的结果。其中有理数蓝桥杯2022年第十三届省赛真题爬树的甲壳虫2对质数 P 取模的结果是整数 c 满足 0 ≤ c < P 且 c · b ≡ a (mod P)。

• 样例输入
  1
  1 2

• 样例输出
  2

• 提示
  对于 20% 的评测用例，n ≤ 2，1 ≤ xi < yi ≤ 20 ；
  对于 50% 的评测用例，n ≤ 500，1 ≤ xi < yi ≤ 200 ；
  对于所有评测用例，1 ≤ n ≤ 100000，1 ≤ xi < yi ≤ 10^9 。

题目G:全排列的价值 （20分）

• 题目描述
  题目描述：对于一个排列 A = (a1, a2, · · · , an)，定义价值 ci 为 a1 至 ai−1 中小于 ai 的数的个数，即 bi = |{aj | j < i, aj < ai}|。定义 A 的价值为。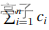
  给定 n，求 1 至 n 的全排列中所有排列的价值之和。

• 输入格式
  输入一行包含一个整数 n 。

• 输出格式
  输出一行包含一个整数表示答案，由于所有排列的价值之和可能很大，请输出这个数除以 998244353 的余数。

• 样例输入
  3

• 样例输出
  9

• 提示
  1 至 3 构成的所有排列的价值如下:
  (1, 2, 3) : 0 + 1 + 2 = 3 ；
  (1, 3, 2) : 0 + 1 + 1 = 2 ；
  (2, 1, 3) : 0 + 0 + 2 = 2 ；
  (2, 3, 1) : 0 + 1 + 0 = 1 ；
  (3, 1, 2) : 0 + 0 + 1 = 1 ；
  (3, 2, 1) : 0 + 0 + 0 = 0 ；
  故总和为 3 + 2 + 2 + 1 + 1 = 9。
  对于 40% 的评测用例，n ≤ 20 ；
  对于 70% 的评测用例，n ≤ 5000 ；
  对于所有评测用例，2 ≤ n ≤ 10^6 。

题目H:扫描游戏 （20分）

• 题目描述
  有一根围绕原点 O 顺时针旋转的棒 OA，初始时指向正上方（Y 轴正向）。 在平面中有若干物件，第 i 个物件的坐标为 (xi , yi) ，价值为 zi。当棒扫到某个物件时，棒的长度会瞬间增长 zi，且物件瞬间消失（棒的顶端恰好碰到物件也视为扫到），如果此时增长完的棒又额外碰到了其他物件，也按上述方式消去 （它和上述那个点视为同时消失）。
  如果将物件按照消失的时间排序，则每个物件有一个排名，同时消失的物件排名相同，请输出每个物件的排名，如果物件永远不会消失则输出 −1。

• 输入格式
  输入第一行包含两个整数 n、L，用一个空格分隔，分别表示物件数量和棒的初始长度。
  接下来 n 行每行包含第三个整数 xi , yi ,zi。

• 输出格式
  输出一行包含 n 整数，相邻两个整数间用一个空格分隔，依次表示每个物件的排名。

• 样例输入
  5 2
  0 1 1
  0 3 2
  4 3 5
  6 8 1
  -51 -33 2

• 样例输出
  1 1 3 4 -1

• 提示
  对于 30% 的评测用例，1 ≤ n ≤ 500 ；
  对于 60% 的评测用例，1 ≤ n ≤ 5000 ；
  对于所有评测用例，1 ≤ n ≤ 200000，−10^9 ≤ xi , yi ≤ 10^9，1 ≤ L,zi ≤ 10^9 。

题目I:数的拆分 （25分）

• 题目描述
  给定 T 个正整数 ai，分别问每个 ai 能否表示为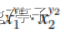
  的形式，其中 x1, x2 为正整数，y1, y2 为大于等于 2 的正整数。

• 输入格式
  输入第一行包含一个整数 T 表示询问次数。
  接下来 T 行，每行包含一个正整数 ai 。

• 输出格式
  对于每次询问, 如果 ai 能够表示为题目描述的形式则输出 yes，否则输出 no 。

• 样例输入
  7
  2
  6
  12
  4
  8
  24
  72

• 样例输出
  no
  no
  no
  yes
  yes
  no
  yes

• 提示
  第 4,5,7 个数分别可以表示为：
  a4 = 22 × 12 ；
  a5 = 23 × 12 ；
  a7 = 23 × 32 。
  【评测用例规模与约定】
  对于 10% 的评测用例，1 ≤ T ≤ 200，ai ≤ 10^9 ；
  对于 30% 的评测用例，1 ≤ T ≤ 300，ai ≤ 10^18 ；
  对于 60% 的评测用例，1 ≤ T ≤ 10000，ai ≤ 10^18 ；
  对于所有评测用例，1 ≤ T ≤ 100000，1 ≤ ai ≤ 10^18 。

题目J:重复的数 （25分）

• 题目描述
  给定一个数列 A = (a1, a2, · · · , an)，给出若干询问，每次询问某个区间 [li ,ri ] 内恰好出现 ki 次的数有多少个。

• 输入格式
  输入第一行包含一个整数 n 表示数列长度。
  第二行包含 n 个整数 a1, a2, · · · , an，表示数列中的数。
  第三行包含一个整数 m 表示询问次数。
  接下来 m 行描述询问，其中第 i 行包含三个整数 li ,ri , ki 表示询问 [li ,ri ] 区间内有多少数出现了 ki 次。

• 输出格式
  输出 m 行，分别对应每个询问的答案。

• 样例输入
  3
  1 2 2
  5
  1 1 1
  1 1 2
  1 2 1
  1 2 2
  1 3 2

• 样例输出
  1
  0
  2
  0
  1

• 提示
  对于 20% 的评测用例，n, m ≤ 500, 1 ≤ a1, a2, · · · , an ≤ 1000；
  对于 40% 的评测用例，n, m ≤ 5000；
  对于所有评测用例，1 ≤ n, m ≤ 100000, 1 ≤ a1, a2, · · · , an ≤ 100000, 1 ≤ li ≤ ri ≤ n, 1 ≤ ki ≤ n。