生成哈夫曼树 - 华为OD统一考试(C卷)_生成哈夫曼树华为od

OD统一考试（C卷）

分值： 100分

题解： Java / Python / C++

题目描述

给定长度为 n 的无序的数字数组，每个数字代表二叉树的叶子节点的权值，数字数组的值均大于等于 1 。

请完成一个函数，根据输入的数字数组，生成哈夫曼树，并将哈夫曼树按照中序遍历输出。

为了保证输出的二叉树中序遍历结果统一，增加以下限制:

• 在树节点中，左节点权值小于等于右节点权值，根节点权值为左右节点权值之和。
• 当左右节点权值相同时，左子树高度高度小于等于右子树。

注意: 所有用例保证有效，并能生成哈夫曼树提醒:哈夫曼树又称最优二叉树，是一种带权路径长度最短的一叉树。

所谓树的带权路径长度，就是树中所有的叶结点的权值乘上其到根结点的路径长度(若根结点为 0 层，叶结点到根结点的路径长度为叶结点的层数)

输入描述

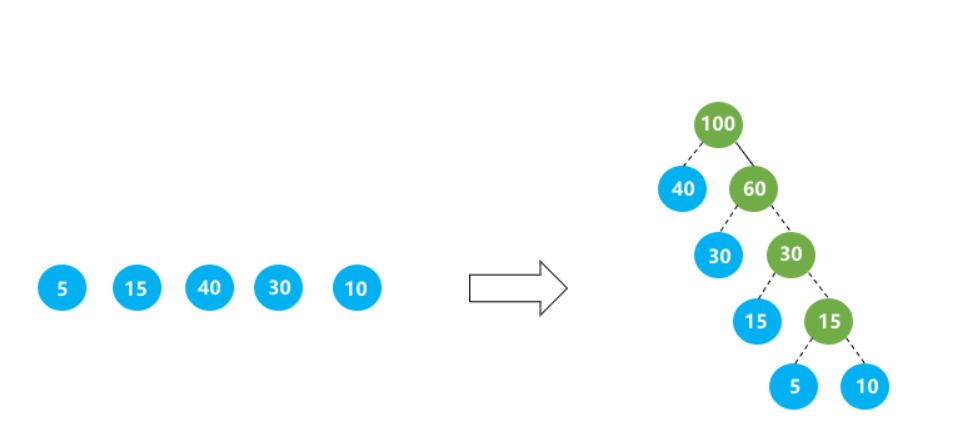
例如：由叶子节点 5 15 40 30 10 生成的最优二叉树如下图所示，该树的最短带权路径长度为 40∗1+30∗2+15∗3+5∗4+10∗4=205。

输出描述

输出一个哈夫曼的中序遍历数组，数值间以空格分隔

示例1

输入：
5
5 15 40 30 10

输出：
40 100 30 60 15 30 5 15 10

说明：
根据输入，生成哈夫曼树，按照中序遍历返回。所有节点中，左节点权值小于等于右节点权值之和。当左右节点权值相同时左子树高度小于右子树。结果如上图
1
2
3
4
5
6
7
8
9

题解

这是一个构建哈夫曼树并进行中序遍历的问题。下面是对解题思路和代码的一些解释：

1. 定义了一个 Node 类（C++中是结构体），表示哈夫曼树的节点。其中，weight 表示权值，height 表示树的高度，left 和 right 分别表示左子树和右子树。
2. 重载了 Node 的比较运算符，以便在优先队列（小顶堆）中按照规定的比较规则进行排序。比较规则是先按照权值升序排列，如果权值相同，则按照树高度升序排列。
3. 使用优先队列（小顶堆）来存储节点，确保每次取出的节点都是权值最小的节点。
4. 通过输入构建节点，将节点加入优先队列。
5. 使用优先队列构建哈夫曼树，每次取出两个最小的节点，合并为一个新节点，再放回队列，直到队列中只剩一个节点为止。
6. 最终得到哈夫曼树的根节点，通过中序遍历输出结果。

对于时间复杂度和空间复杂度：

• 时间复杂度：构建哈夫曼树的过程中，每次取出两个最小节点，因此时间复杂度为 O(n log n)，其中 n 为节点的个数。
• 空间复杂度：使用了优先队列来存储节点，空间复杂度为 O(n)。

---

哈夫曼树（Huffman Tree）是一种用于编码的二叉树，其中每个叶子节点表示一个字符，而每个内部节点包含一个权值，表示字符出现的频次。哈夫曼树的构建目标是最小化编码长度，使得出现频次较高的字符拥有较短的编码。

构建哈夫曼树的步骤如下：

1. 给定一组字符及其频次，将每个字符视为一个权值为其频次的单节点树。
2. 从这些单节点树中选择两个具有最小权值的树，合并成一个新的树，新树的权值为两个原树的权值之和。这一步骤称为构建哈夫曼树的一次合并操作。
3. 重复步骤2，直到只剩下一个树，即哈夫曼树。

在构建的过程中，为了确保编码长度最短，频次越高的字符在树中的深度越浅。

哈夫曼树主要用于数据压缩，其中对字符进行编码时，频次高的字符用较短的二进制编码表示，频次低的字符用较长的编码表示，从而实现对数据的高效压缩。

Java

import java.util.PriorityQueue;
import java.util.Scanner;

class Node implements Comparable<Node> {
    long weight;       // 权值
    int height;        // 树高度
    Node left, right;  // 左右子树

    public Node() {
        this.height = 1;
        this.left = null;
        this.right = null;
    }

    // 重载小于运算符，用于定义小顶堆中的比较规则
    @Override
    public int compareTo(Node other) {
        if (this.weight != other.weight) {
            return Long.compare(this.weight, other.weight);  // 小顶堆，按照权值升序排列
        } else {
            return Integer.compare(this.height, other.height);  // 权值相同，则树高度升序排序
        }
    }
}
/**
 * @author code5bug
 */
public class Main {

    // 中序遍历
    static void inorder(Node node) {
        if (node == null) return;
        inorder(node.left);
        System.out.print(node.weight + " ");
        inorder(node.right);
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        PriorityQueue<Node> minHeap = new PriorityQueue<>();

        for (int i = 0; i < n; i++) {
            Node node = new Node();
            node.weight = scanner.nextLong();
            minHeap.offer(node);
        }

        // 生成哈夫曼树，使用小顶堆，每次取出两个最小的节点，合并为一个新节点，再放回去，直到只剩一个节点为止。
        while (minHeap.size() > 1) {
            Node left = minHeap.poll();
            Node right = minHeap.poll();

            Node pnode = new Node();
            pnode.weight = left.weight + right.weight;
            pnode.height = Math.max(left.height, right.height) + 1;
            pnode.left = left;
            pnode.right = right;

            minHeap.offer(pnode);
        }

        Node root = minHeap.poll();
        inorder(root);
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67

Python

import heapq

class Node:
    def __init__(self):
        self.weight = 1
        self.height = 1
        self.left = None
        self.right = None

    # 重载小于运算符，用于定义小顶堆中的比较规则
    def __lt__(self, other):
        if self.weight != other.weight:
            return self.weight < other.weight  # 小顶堆，按照权值升序排列
        else:
            return self.height < other.height  # 权值相同，则树高度升序排序

# 中序遍历
def inorder(node):
    if node is None:
        return
    inorder(node.left)
    print(node.weight, end=" ")
    inorder(node.right)

def main():
    n = int(input())
    min_heap = []

    for weight in map(int, input().split()):
        node = Node()
        node.weight = weight
        heapq.heappush(min_heap, node)

    # 生成哈夫曼树，使用小顶堆，每次取出两个最小的节点，合并为一个新节点，再放回去，直到只剩一个节点为止。
    while len(min_heap) > 1:
        left = heapq.heappop(min_heap)
        right = heapq.heappop(min_heap)

        pnode = Node()
        pnode.weight = left.weight + right.weight
        pnode.height = max(left.height, right.height) + 1
        pnode.left = left
        pnode.right = right

        heapq.heappush(min_heap, pnode)

    root = min_heap[0]
    inorder(root)

if __name__ == "__main__":
    main()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

C++

#include <bits/stdc++.h>
using namespace std;

struct Node
{
    long long weight;         // 权值
    int       height;         // 树高度
    Node *    left, *right;   // 左右子树
    Node()
        : height(1)
        , left(nullptr)
        , right(nullptr)
    {}

    // 重载小于运算符，用于定义小顶堆中的比较规则
    bool operator<(const Node& other) const
    {
        if (weight != other.weight) {
            return weight > other.weight;   // 小顶堆，按照权值升序排列
        } else {
            return height > other.height;   // 权值相同，则树高度升序排序
        }
    }
};

// 中序遍历
void inorder(const Node* node)
{
    if (node == nullptr) return;
    inorder(node->left);
    cout << node->weight << " ";
    inorder(node->right);
}

int main()
{
    int n = 0;
    cin >> n;
    priority_queue<Node> min_heap;

    for (int i = 0; i < n; i++) {
        Node node;
        cin >> node.weight;
        min_heap.push(node);
    }

    // 生成 哈夫曼树，使用小顶堆，每次取出两个最小的节点，合并为一个新节点，再放回去，直到只剩一个节点为止。
    while (min_heap.size() > 1) {
        Node left = min_heap.top();
        min_heap.pop();

        Node right = min_heap.top();
        min_heap.pop();

        Node pnode;
        pnode.weight = left.weight + right.weight;
        pnode.height = max(left.height, right.height) + 1;
        pnode.left   = new Node(left);    // 使用移动构造函数
        pnode.right  = new Node(right);   // 使用移动构造函数

        min_heap.push(pnode);
    }

    Node root = min_heap.top();
    min_heap.pop();
    inorder(&root);

    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

‍❤️‍华为OD机试面试交流群（每日真题分享）： 加V时备注“华为od加群”