图像处理中的一些概念(补充)_图像高频和低频是怎么界定的

高频信号理解和频域(fft得到)中的高通滤波器进行边检

高频信号

高频分量(高频信号)：对应着图像变化剧烈的部分，也就是图像的边缘（轮廓）或者噪声以及细节部分。 主要是对图像边缘和轮廓的度量，而人眼对高频分量比较敏感。之所以说噪声也对应着高频分量，是因为图像噪声在大部分情况下都是高频的。

空间频率指的是图像中灰度值相对它的邻居点变化方式。如果一副图像中灰度从一边到另一边变化很小，那就说这副图像是低频信号。如果某些像素相对于它邻近的像素点变化很剧烈，则说明该图像含有高频信号.

一般纹理、物体的边缘、角点多为高频信号。具体就是图像中剧烈的灰度变化的地方具有较高的高频分量。

利用傅里叶变化来解释高频

网上有一个解释非常形象：将傅里叶变换比作一个玻璃棱镜。棱镜是可以将光分解为不同颜色的物理仪器，每个成分的颜色由波长（或频率）来决定。

傅里叶变换可以看作是数学上的棱镜，将函数基于频率分解为不同的成分。当我们考虑光时,讨论它的光谱或频率谱。同样,傅立叶变换使我们能通过频率成分来分析一个函数。

**图像的频率是表征图像中灰度变化剧烈程度(梯度)的指标，是灰度在平面空间上的梯度。**如：大面积的沙漠在图像中是一片灰度变化缓慢的区域，对应的频率值很低；而对于地表属性变换剧烈的边缘区域在图像中是一片灰度变化剧烈的区域，对应的频率值较高。

从纯粹的数学意义上看，傅立叶变换是将一个函数转换为一系列周期函数来处理的。

从物理效果看，傅立叶变换是将图像从空间域转换到频率域，傅立叶变换的物理意义是将****图像的灰度分布函数变换为图像的频率分布函数****，傅立叶逆变换是将图像的频率分布函数变换为灰度分布函数。

图像进行二维傅立叶变换得到频谱图，就是图像梯度的分布图，如下图所示，右图为左图的频谱图。

注意：频谱图上的各点与图像上各点并不存在一一对应的关系，即使在不移频的情况下也是没有。傅立叶频谱图上我们看到的明暗不一的亮点，实际是上图像上某一点与邻域点差异的强弱，即梯度的大小，也即该点的频率的大小（可以这么理解，图像中的低频部分指低梯度的点，高频部分相反）。

我的一点理解

我们在学习图像频率滤波，能看出来，频域上操作的效果比空间域上操作的效果好。但是很难理解为什么要这么做。其实可以这么理解，例如，有一幅含噪声的图像，若对图像进行空间域操作，使用均值滤波，那么噪声未知的像素点会被周围像素点求均值取代，可能效果会比原图好一点，但是这对原有图像的有些信息造成损失(像素取均值)。

那么将图像在频率域上进行操作，噪声在频率上反映是高频信息，通过设置相应的滤波器，滤除噪声。然后从频域还原回来。此时图像的有用的信息不会损失。

频率域滤波

低通滤波器：使低频通过而使高频衰减的滤波器
1.被低通滤波的图像比原始图像少尖锐的细节部分而突出平滑过渡部分
2.对比空间域滤波的平滑处理，如均值滤波器

高通滤波器：使高频通过而使低频衰减的滤波器
1.被高通滤波的图像比原始图像少灰度级的平滑过渡而突出边缘等细节部分
2.对比空间域的梯度算子、拉普拉斯算子

频率域下进行高通滤波器滤波

中心的亮点反映的是图像低频信息，也就是图像的平滑部分，因平滑部分所占图像的比例较高，故能量高；而图像的边缘信息，也就是高频信息，即图像突变比较多的地方相对较少，因此能量低。而能量越高，在频谱图中所表现出来的就越亮。

原图像频谱(中间亮的表示低频信息，因为平滑部分所占图像的比例较高，越多在频谱中越亮)

高通滤波器(去掉中间亮的部分，也就是去掉低频区，保留高频的，形成边缘)

在频域下使用高通滤波器进行滤波：

黑色为0，白色为1，把这个模板去和图像进过傅里叶变换的频域矩阵去与（相乘）一下就实现了高通滤波。比如下面：

import cv2
import numpy as np
import matplotlib.pyplot as plt
 
img_man = cv2.imread('woman.jpg',0) #直接读为灰度图像
plt.subplot(121),plt.imshow(img_man,'gray'),plt.title('origial')
plt.xticks([]),plt.yticks([])
#--------------------------------
# 构造高通滤波器
rows,cols = img_man.shape
mask = np.ones(img_man.shape,np.uint8)
mask[rows/2-30:rows/2+30,cols/2-30:cols/2+30] = 0
 
#--------------------------------
# fft转换为频域
f1 = np.fft.fft2(img_man)
# 将低频点移至中心
f1shift = np.fft.fftshift(f1)
# 进行高通滤波
f1shift = f1shift*mask
# 然后把之前移至中心的操作复原
f2shift = np.fft.ifftshift(f1shift) #对新的进行逆变换
# 逆变换
img_new = np.fft.ifft2(f2shift)
 
#出来的是复数，无法显示
 
img_new = np.abs(img_new)
 
#调整大小范围便于显示
 
img_new = (img_new-np.amin(img_new))/(np.amax(img_new)-np.amin(img_new))
 
plt.subplot(122),plt.imshow(img_new,'gray'),plt.title('Highpass')
 
plt.xticks([]),plt.yticks([])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

fftshift

作用：将零频点(也就是低频点)移到频谱的中间

由于低频点数量多所以中间显得亮

用法：

Y=fftshift(X)
Y=fftshift(X，dim)

描述：fftshift移动零频点到频谱中间，重新排列fft,fft2和fftn的输出结果。将零频点放到频谱的中间对于观察傅立叶变换是有用的。

卷积神经网络名词介绍

空间金字塔池化技术(spatial pyramid pooling，SSP)

convolution和polling都对输入图片的大小不敏感，而全连接层却敏感。

卷积网络的参数主要是卷积核，完全能够适用任意大小的输入，并且能够产生任意大小的输出。但是全连接层部分不同，全连接层部分的参数是神经元对于所有输入的连接权重，也就是说输入尺寸不固定的话，全连接层参数的个数都不能固定

引入空间金字塔池化层代替池化层，在网络的全连接层前面加一层金字塔pooling层解决输入图片大小不一的情况

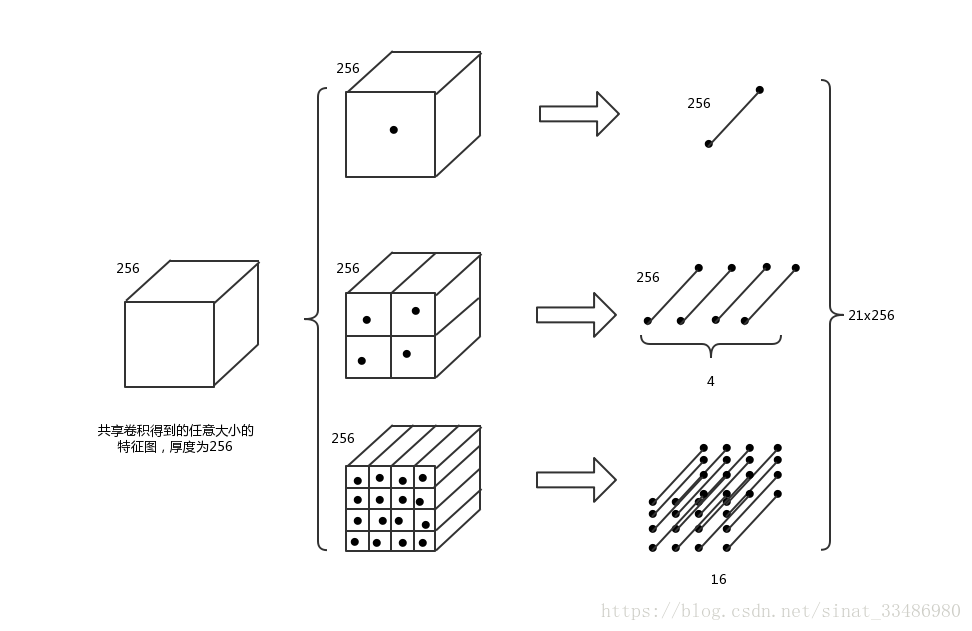
spatital pyramid pooling layer就是把前一卷积层的feature maps的每一个图片上进行了3个卷积操作。最右边的就是原图像，中间的是把图像分成大小是4的特征图，最右边的就是把图像分成大小是16的特征图。 那么每一个feature map就会变成16+4+1=21个feature maps。这不就解决了特征图大小不一的状况了吗？

如图所示，对于选择的不同大小的区域对应到卷积之后的特征图上，得到的也是大小不一致的特征图区域，厚度为256，对于每个区域（厚度为256），通过三种划分方式进行池化：

（1）直接对整个区域池化，每层得到一个点，共256个点，构成一个1x256的向量

（2）将区域划分成2x2的格子，每个格子池化，得到一个1x256的向量，共2x2=4个格子，最终得到4个1x256的向量

（3）将区域划分成4x4的格子，每个格子池化，得到一个1x256的向量，共4x4=16个格子，最终得到16个1x256的向量

将三种划分方式池化得到的结果进行拼接，得到$(1+4+16)\ast 256=21\ast 256$的特征。

从这21个块中，每个块提取出一个特征，这样刚好就是我们要提取的21维特征向量。

第一张图片,我们把一张完整的图片，分成了16个块，也就是每个块的大小就是(w/4,h/4);

第二张图片，划分了4个块，每个块的大小就是(w/2,h/2);

第三张图片，把一整张图片作为了一个块，也就是块的大小为(w,h)

空间金字塔最大池化的过程，其实就是从这21个图片块中，分别计算每个块的最大值，从而得到一个输出神经元。最后把一张任意大小的图片转换成了一个固定大小的21维特征（当然你可以设计其它维数的输出，增加金字塔的层数，或者改变划分网格的大小）。上面的三种不同刻度的划分，每一种刻度我们称之为：金字塔的一层，每一个图片块大小我们称之为：windows size了。如果你希望，金字塔的某一层输出n*n个特征，那么你就要用windows size大小为：(w/n,h/n)进行池化了。

理解：也就是根据图片大小，分别划分为16个块，4块，1块。然后分别对三个划分后的图片进行池化，每一个块池化为一个特征值。加起来的话得到21个特征点。这个不依赖于图片大小，多大的图片都能这样搞到21个特征，也就是池化的那个滤波器大小会随着图片大小变化。

简单的两层网络

输入层：一张任意大小的图片,假设其大小为(w,h)。

输出层：21个神经元。

也就是我们输入一张任意大小的特征图的时候，我们希望提取出21个特征

当我们有很多层网络的时候，当网络输入的是一张任意大小的图片，这个时候我们可以一直进行卷积、池化，直到网络的倒数几层的时候，也就是我们即将与全连接层连接的时候，就要使用金字塔池化，使得任意大小的特征图都能够转换成固定大小的特征向量，这就是空间金字塔池化的奥义（多尺度特征提取出固定大小的特征向量）。

SSP优点：

金字塔池化层有如下的三个优点，

第一：他可以解决输入图片大小不一造成的缺陷。

第二：由于把一个feature map从不同的角度进行特征提取，再聚合的特点，显示了算法的robust的特性。

第三：同时也在object recongtion增加了精度。

其实，你也可以这样想，最牛掰的地方是因为在卷积层的后面对每一张图片都进行了多方面的特征提取，他就可以提高任务的精度。好比是不同大小的图片在不同的网络中进行训练一样，大大提高了模型的精度。

感受野

卷积是对特定小区域的特征提取，比如一张 300×300300×300 的原图经过一定卷积操作之后得到 8×88×8 的特征图，特征图上的每个“像素点”其实对应原图的一个“感受野”，在这里一个“感受野”的大小为 3008×30083008×3008 也即 37.5×37.537.5×37.5 （实际上不可能有.5.5，是3737还是3838要看卷积过程是否padding）。

换句话说，特征图左上角的一个感受野其实是原图左上角一个 37.5×37.537.5×37.5 大小区域的一个特征抽取（或者说是这个区域的一个抽象化，融合了这个区域的信息）。

R-CNN：区域(Region)卷积神经网络

这是基于卷积神经网络的物体检测的奠基之作。其核心思想是在对每张图片选取多个区域，然后每个区域作为一个样本进入一个卷积神经网络来抽取特征，最后使用分类器(SVM)来对齐分类，和一个回归器(边框回归)来得到准确的边框。

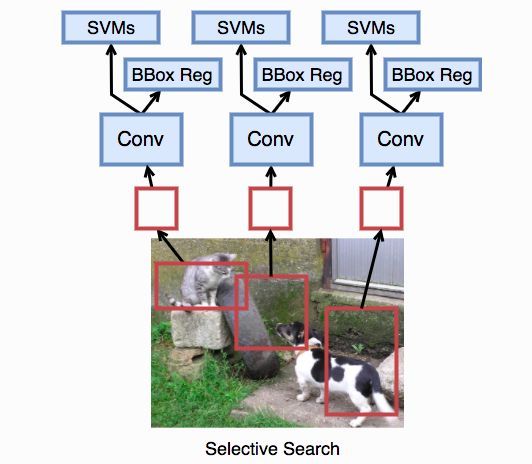
具体来说，这个算法有如下几个步骤：

1. 对每张输入图片使用一个基于规则的“选择性搜索”算法来选取多个提议区域
2. 跟微调迁移学习里那样，选取一个预先训练好的卷积神经网络并去掉最后一个输入层。每个区域被调整成这个网络要求的输入大小并计算输出。这个输出将作为这个区域的特征。
3. 使用这些区域特征来训练多个SVM来做物体识别，每个SVM预测一个区域是不是包含某个物体
4. 使用这些区域特征来训练线性回归器将提议区域

直观上R-CNN很好理解，但问题是它可能特别慢。一张图片我们可能选出上千个区域，导致一张图片需要做上千次预测。虽然跟微调不一样，这里训练可以不用更新用来抽特征的卷积神经网络，从而我们可以事先算好每个区域的特征并保存。但对于预测，我们无法避免这个。从而导致R-CNN很难实际中被使用。

Fast R-CNN：快速的区域卷积神经网络

Fast R-CNN对R-CNN主要做了两点改进来提升性能。

1. 考虑到R-CNN里面的大量区域可能是相互覆盖，每次重新抽取特征过于浪费。因此Fast R-CNN先对输入图片抽取特征，然后再选取区域
2. 代替R-CNN使用多个SVM来做分类，Fast R-CNN使用单个多类逻辑回归，这也是前面教程里默认使用的。

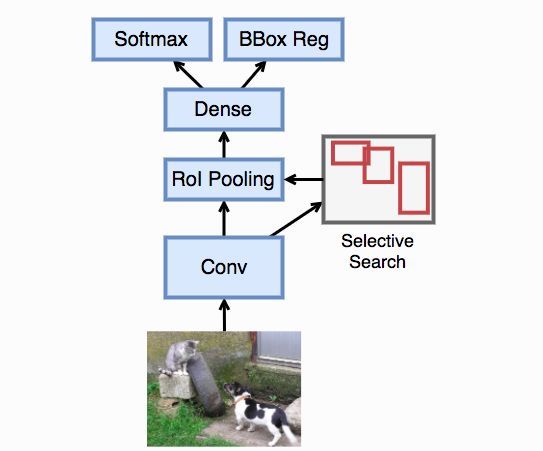
从示意图可以看到，使用选择性搜索选取的区域是作用在卷积神经网络提取的特征上。这样我们只需要对原始的输入图片做一次特征提取即可，如此节省了大量重复计算。

ROI 感兴趣区域

Fast R-CNN提出兴趣区域池化层（Region of Interest (RoI) pooling），它的输入为特征和一系列的区域，对每个区域它将其均匀划分成n×m 的小区域，并对每个小区域做最大池化，从而得到一个n×m 的输出。因此不管输入区域的大小，RoI池化层都将其池化成固定大小输出。

Fast R-CNN沿用了R-CNN的选择性搜索方法来选择区域。这个通常很慢。Faster R-CNN做的主要改进是提出了区域提议网络（region proposal network, RPN）来替代选择性搜索。它是这么工作的：

1. 在输入特征上放置一个填充为1通道是256的3 × 3卷积。这样每个像素，连同它的周围8个像素，都被映射成一个长为256的向量。
2. 以对每个像素为中心生成数个大小和长宽比预先设计好的k 个默认边框，通常也叫锚框。
3. 对每个边框，使用其中心像素对应的256维向量作为特征，RPN训练一个2类分类器来判断这个区域是不是含有任何感兴趣的物体还是只是背景，和一个4维输出的回归器来预测一个更准确的边框。
4. 对于所有的锚框，个数为$nmk $如果输入大小是n × m ，选出被判断出含有物体的，然后将他们对应的回归器预测的边框作为输入放进接下来的RoI池化层

虽然看上有些复杂，但RPN思想非常直观。首先提议预先配置好的一些区域，然后通过神经网络来判断这些区域是不是感兴趣的，如果是，那么再预测一个更加准确的边框。这样我们能有效降低搜索任何形状的边框的代价。

Mask R-CNN

Mask R-CNN在Faster R-CNN上加入了一个新的像素级别的预测层，它不仅对一个锚框预测它对应的类和真实的边框，而且它会判断这个锚框类每个像素对应的哪个物体还是只是背景。后者是语义分割要解决的问题。Mask R-CNN使用了之后我们将介绍的全连接卷积网络(FCN)来完成这个预测。当然这也意味这训练数据必须有像素级别的标注，而不是简单的边框。

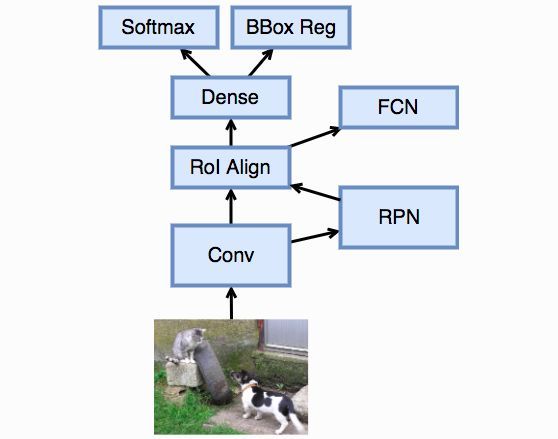
因为FCN会精确预测每个像素的类别，就是输入图片中的每个像素都会在标注中对应一个类别。对于输入图片中的一个锚框，我们可以精确的匹配到像素标注中对应的区域。但是RoI池化是作用在卷积之后的特征上，其默认是将锚框做了定点化。例如假设选择的锚框是( x , y , w , h ) ，且特征抽取将图片变小了16倍，就是如果原始图片是256 × 256 ，那么特征大小就是16 × 16 。这时候在特征上对应的锚框就是变成了( ⌊ x / 16 ⌋ , ⌊ y / 16 ⌋ , ⌊ w / 16 ⌋ , ⌊ h / 16 ⌋ ) 。如果x , y , w , h 中有任何一个不被16整除，那么就可能发生错位。同样道理，在上面的样例中我们看到，如果锚框的长宽不被池化大小整除，那么同样会定点化，从而带来错位。

通常这样的错位只是在几个像素之间，对于分类和边框预测影响不大。但对于像素级别的预测，这样的错位可能会带来大问题。Mask R-CNN提出一个RoI Align层，它类似于RoI池化层，但是去除掉了定点化步骤，就是移除了所有⌊ ⋅ ⌋ 。如果计算得到的表框不是刚好在像素之间，那么我们就用四周的像素来线性插值得到这个点上的值。

对于一维情况，假设我们要计算x 点的值f ( x ) ，那么我们可以用x 左右的整点的值来插值：

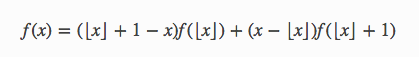
我们实际要使用的是二维差值来估计f ( x , y ) ，我们首先在x 轴上差值得到f ( x , ⌊ y ⌋ ) 和f ( x , ⌊ y ⌋ + 1 ) ，然后根据这两个值来差值得到f ( x , y ) .

SSD 单发多框检测(single shot multibox detection)

在R-CNN系列模型里。区域提议和分类是分作两块来进行的。SSD则将其统一成一个步骤来使得模型更加简单并且速度更快，这也是为什么它被称之为单发的原因。

它跟Faster R-CNN主要有两点不一样

1. 对于锚框，我们不再首先判断它是不是含有感兴趣物体，再将正类锚框放入真正物体分类。SSD里我们直接使用一个num_class+1类分类器来判断它对应的是哪类物体，还是只是背景。我们也不再有额外的回归器对边框再进一步预测，而是直接使用单个回归器来预测真实边框。
2. SSD不只是对卷积神经网络输出的特征做预测，它会进一步将特征通过卷积和池化层变小来做预测。这样达到多尺度预测的效果。

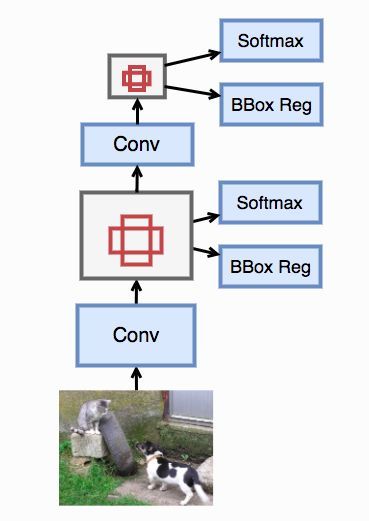
YOLO：只需要看一遍

不管是Faster R-CNN还是SSD，它们生成的锚框仍然有大量是相互重叠的，从而导致仍然有大量的区域被重复计算了。YOLO试图来解决这个问题。它将图片特征均匀的切成 S × S 块，每一块当做一个锚框。每个锚框预测B 个边框，以及这个锚框主要包含哪个物体。

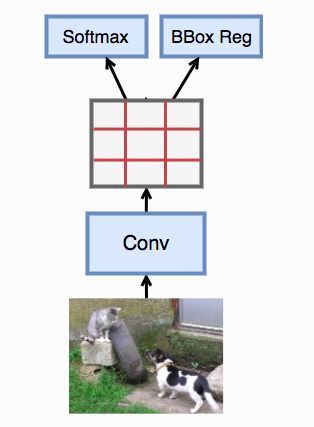
Yolo

YOLO v2：更好，更块，更强

YOLO v2对YOLO进行一些地方的改进，其主要包括：

1. 使用更好的卷积神经网络来做特征提取，使用更大输入图片448 × 448 使得特征输出大小增大到13 × 13
2. 不再使用均匀切来的锚框，而是对训练数据里的真实锚框做聚类，然后使用聚类中心作为锚框。相对于SSD和Faster R-CNN来说可以大幅降低锚框的个数。
3. 不再使用YOLO的全连接层来预测，而是同SSD一样使用卷积。例如假设使用5个锚框（聚类为5类），那么物体分类使用通道数是5*(1+num_classes)的1 × 1 卷积，边框回归使用通道数4*5.

我们描述了基于卷积神经网络的几个物体检测算法。他们之间的共同点在于首先提出锚框，使用卷积神经网络抽取特征后来预测其包含的主要物体和更准确的边框。但他们在锚框的选择和预测上各有不同，导致他们在计算实际和精度上也各有权衡。

PS：

BBox Reg(边框回归(Bounding Box Regression))

Bounding-box regression 就是用来微调这个窗口的。使得经过微调后的窗口跟Ground Truth 更接近

Ground Truth

正确的t标注是ground truth，也有人将所有标注数据都叫做ground truth

IOU 交并比（Intersection over Union）

IoU 的全称为交并比（Intersection over Union），通过这个名称我们大概可以猜到 IoU 的计算方法。IoU 计算的是 “预测的边框” 和 “真实的边框” 的交集和并集的比值。

ssion))

Bounding-box regression 就是用来微调这个窗口的。使得经过微调后的窗口跟Ground Truth 更接近

Ground Truth

正确的t标注是ground truth，也有人将所有标注数据都叫做ground truth

IOU 交并比（Intersection over Union）

IoU 的全称为交并比（Intersection over Union），通过这个名称我们大概可以猜到 IoU 的计算方法。IoU 计算的是 “预测的边框” 和 “真实的边框” 的交集和并集的比值。

全连接层 (Fully Connected Layer,FCL)