深度探索：机器学习岭回归（Ridge Regression）算法原理及其应用_岭回归模型原理

目录

1. 引言与背景

2. Ridge Regression 定理

3. 算法原理

4. 算法实现

5. 优缺点分析

   优点：

   缺点：

6. 案例应用

7. 对比与其他算法

8. 结论与展望

---

1. 引言与背景

   在机器学习和统计学领域，回归分析是一种重要的预测建模技术，用于研究变量之间的关系以及估计因变量基于自变量的变化情况。其中，岭回归（Ridge Regression）作为一种线性模型正则化方法，在处理多重共线性、过拟合等问题上具有显著的优势。当特征之间高度相关，即存在多重共线性时，普通最小二乘法可能导致系数估计值不稳定且方差过大，进而影响模型的泛化能力。因此，岭回归在维持模型解释力的同时，通过对系数向量添加L2范数惩罚项来约束模型复杂度，从而改善模型性能，降低了模型过拟合的风险。

   随着大数据时代海量特征数据的涌现，岭回归因其在稀疏性和稳定性方面的优良特性，在金融风险控制、生物医学数据分析、信号处理等领域得到广泛应用，成为众多实际问题求解的重要工具。

2. Ridge Regression 定理

   岭回归的核心数学表达式可以通过优化目标函数来阐述。对于给定的训练样本集 {(x_1, y_1), (x_2, y_2), ..., (x_n, y_n)} ，其中是自变量向量， 是因变量，岭回归的目标是最小化加权残差平方和与系数向量L2惩罚项之和：

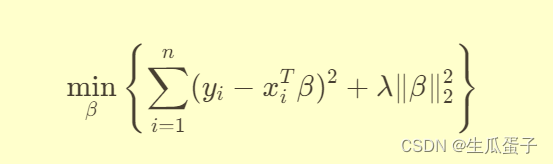
   其中，β是回归系数向量，λ化参数，它决定了惩罚项的权重，直接关系到模型的复杂度控制程度。通过求解该优化问题可得岭回归系数的解析解或数值解。

3. 算法原理

   岭回归的主要原理在于引入L2正则化。正则化的作用在于限制模型参数的增长幅度，通过增加惩罚项使得那些对预测贡献较小但会增大模型复杂度的系数被“压缩”，降低其绝对值。同时，由于L2正则化会产生一个圆形的约束边界，故又称为L2范数惩罚或权重衰减。

   对于上述目标函数，当引入拉格朗日乘子后，可通过求导数并将导数置零获得岭回归的解析解。解出的系数 $\beta$ 包含了对所有特征的权重分配，而 $\lambda$ 的选择通常通过交叉验证或使用网格搜索结合验证集误差来确定最优值。

4. 算法实现

Python中实现岭回归（Ridge Regression）可以借助于scikit-learn库，这是一个强大的机器学习库，内含了大量的机器学习算法实现，包括岭回归。以下是使用scikit-learn实现岭回归的基本步骤和代码详解：

# 导入所需库
from sklearn.datasets import make_regression  # 生成模拟数据集
from sklearn.model_selection import train_test_split  # 数据集切分
from sklearn.linear_model import Ridge  # 岭回归模型
from sklearn.metrics import mean_squared_error  # 评价指标
import numpy as np
 
# 步骤1：生成模拟数据
# 这里我们生成一个线性回归问题的数据集
n_samples, n_features = 100, 10
X, y = make_regression(n_samples=n_samples, n_features=n_features, noise=0.1, random_state=42)
 
# 步骤2：数据集切分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
 
# 步骤3：初始化岭回归模型
# alpha 参数是正则化强度，其值越大，正则化越强，系数衰减越明显
ridge = Ridge(alpha=1.0)
 
# 步骤4：训练模型
ridge.fit(X_train, y_train)
 
# 步骤5：模型预测
y_pred_train = ridge.predict(X_train)
y_pred_test = ridge.predict(X_test)
 
# 步骤6：评估模型性能
mse_train = mean_squared_error(y_train, y_pred_train)
mse_test = mean_squared_error(y_test, y_pred_test)
 
print(f"Training MSE: {mse_train}")
print(f"Test MSE: {mse_test}")
 
# 你可以调整 alpha 参数寻找最优正则化强度
# 通常使用交叉验证来选择最优 alpha 值
# 例如使用 GridSearchCV 或者通过交叉验证手动遍历一系列 alpha 值
 
# 此外，还可以查看模型学到的系数
# print(f"Coefficients: {ridge.coef_}")

在这个例子中：

• 我们首先使用make_regression函数生成了一个含有100个样本和10个特征的线性回归问题数据集，同时包含了噪声干扰。
• 然后我们将数据集划分为训练集和测试集，以便进行模型训练和性能评估。
• 接着创建了一个Ridge对象，并指定了正则化强度alpha。在岭回归中，alpha控制了正则化力度，更大的alpha值意味着更强的正则化，使得模型更加简洁，但可能会牺牲一部分拟合能力。
• 使用训练数据拟合模型，然后在训练集和测试集上进行预测。
• 最后，我们使用均方误差（MSE）来评估模型在训练集和测试集上的预测性能。

如果你想调整正则化强度以找到最优模型，可以使用交叉验证技术，例如GridSearchCV类来自动生成多个不同alpha值的模型，并选择最优秀的一个。

5. 优缺点分析

   优点：

   - 处理多重共线性：岭回归能够有效缓解因多重共线性导致的标准最小二乘估计不稳定的问题，使得模型在面对高度相关的特征时依然保持较好的预测能力。
   - 防止过拟合：通过L2正则化，岭回归能够在一定程度上避免模型过于复杂，减少过拟合现象的发生。
   - 解的存在唯一性：即使数据矩阵不可逆，岭回归也能保证解的存在性和唯一性。

   缺点：

   - 参数选择：正则化参数 $\lambda$ 的选择对于模型性能至关重要，但往往需要通过经验或特定的交叉验证过程才能找到合适的取值。
   - 模型解释性：相比简单线性回归，正则化后的模型可能会牺牲部分变量的解释性，特别是当某些系数因正则化而趋近于零时。
   - 对于离群点敏感：尽管岭回归在一定程度上增强了模型稳健性，但它仍属于线性模型范畴，对异常值较为敏感。

6. 案例应用

   岭回归在许多领域都有广泛的应用，例如在金融行业用于信贷风险评估，通过对客户特征进行回归分析，预测违约概率；在生物信息学中，用于基因表达数据的分析，识别与某种表型变化显著关联的基因；在信号处理中，可用于滤波器设计及系统辨识等。

7. 对比与其他算法

   相较于普通最小二乘回归，岭回归更适用于数据维度较高或特征之间存在多重共线性的场景。此外，与Lasso回归（L1正则化）相比，岭回归倾向于产生更多非零的小系数（即稀疏性不如Lasso强），但其系数收缩更为平滑，对于特征间的微小差异反应更加敏感。

   Elastic Net回归则是结合了L1和L2正则化的特性，既具备一定的稀疏性，又能应对共线性问题，可以根据具体问题特点灵活选择。

8. 结论与展望

   岭回归作为经典正则化回归方法，在实际应用中展现了强大的适应性和实用性。随着机器学习和统计学理论的发展，未来有望结合现代优化算法和自动调参技术，进一步提升岭回归及其衍生模型在处理大规模数据和复杂问题时的表现。同时，如何在复杂模型集成、深度学习框架中巧妙运用岭回归思想，将是未来值得探索的研究方向。不断优化和改进岭回归算法，使其更好地服务于实际问题，将有助于推动整个数据分析和预测领域的进步与发展。