【skLearn 回归模型】岭回归 ＜linear_model.Ridge＞_sklearn 岭回归

---

---

一、岭回归概念

• 定义

岭回归,又称为吉洪诺夫正则化(Tikhonov regularization)。通常来说,大部分的机器学习教材会使用代数的形式来展现岭回归的原理。这个原理和逻辑回归及支持向量机非常相似,都是将求解w的过程转化为一个带条件的最优化问题,然后用最小二乘法求解。然而,岭回归可以做到的事其实可以用矩阵非常简单地表达出来。岭回归在多元线性回归的损失函数上加上了正则项,表达为系数w的L2范式(即系数w的平方项)乘以正则化系数α。如果你们看其他教材中的代数推导,正则化系数会写作λ ,用以和 Lasso区别,不过在 sklearn中由于是两个不同的算法,因此正则项系数都使用α来代表。

岭回归的损失函数的完整表达式写作:

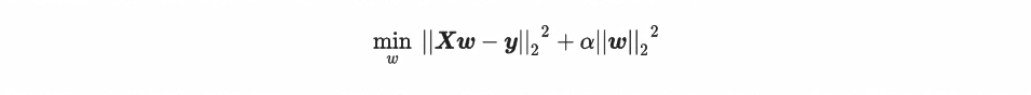
返回顶部

---

• 岭回归处理多重共线性原理

这个操作看起来简单,其实带来了巨大的变化。在线性回归中我们通过在损失函数上对w求导来求解极值,在这里虽然加上了正则项,我们依然使用最小二乘法来求解。假设我们的特征矩阵结构为(m,n),系数w的结构是(1，n)则可以有:



返回顶部

---

二、linear_model.Ridge 类

之前我们在加利佛尼亚房屋价值数据集上使用线性回归,得出的结果大概是训练集上的拟合程度是60%,测试集上的拟合程度也是60%左右,那这个很低的拟合程度是不是由多重共线性造成的呢?在统计学中,我们会通过VF或者各种检验来判断数据是否存在共线性,然而在机器学习中,我们可以使用模型来判断如果一个数据集在岭回归中使用各种正则化参数取值下模型表现没有明显上升(比如出现持平或者下降),则说明数据没有多重共线性,顶多是特征之间有一些相关性。反之,如果一个数据集在岭回归的各种正则化参数取值下表现出明显的上升趋势,则说明数据存在多重共线性。

class sklearn.linear_model.Ridge(alpha=1.0, *, fit_intercept=True, normalize=False, copy_X=True, max_iter=None, 
                                 tol=0.001, solver='auto', random_state=None)[source]
1
2

参数详情参见官方文档：https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Ridge

案例：加利福尼亚房价

加利佛尼亚房屋价值数据集上使用线性回归,得出的结果大概是训练集上的拟合程度是60%,测试集上的拟合程度也是60%左右,那这个很低的拟合程度是不是由多重共线性造成的呢?

① 读取数据集

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge,Lasso,LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.datasets import fetch_california_housing as fch

# 1.加载数据集
house_value = fch()
x = pd.DataFrame(house_value.data)    # 提取数据集
y = house_value.target                # 提取标签
x.columns = ["住户收入中位数","房屋使用年代中位数","平均房间数目","平均卧室数目","街区人口","平均入住率","街区的纬度","街区的经度"]
1
2
3
4
5
6
7
8
9
10
11
12

返回顶部

---

② 划分训练集、测试集

# 2.划分训练集、测试集
xtrain,xtest,ytrain,ytest = train_test_split(x,y,test_size=0.3,random_state=420)
# 2.1训练集恢复索引
for i in [xtrain,xtest]:
    i.index = range(i.shape[0])
1
2
3
4
5

返回顶部

---

③ 岭回归训练模型

# 3.采用岭回归训练模型 --- 定义正则项系数 
reg = Ridge(alpha=1).fit(xtrain,ytrain)
1
2

④ 使用R2系数测评

# 3.1 R2指数
r2_score = reg.score(xtest,ytest) # 0.6043610352312276
1
2

经过几次不同的正则化参数修改，并没有对预测值产生明显的改变(和线性回归基本一样)，所以初步判断，该数据集不存在共线性问题。

返回顶部

---

⑤ 探索交叉验证下，岭回归与线性回归的结果变化

# 4.探索交叉验证下，岭回归与线性回归的结果变化
alpha_range = np.arange(1,1001,100)
ridge,lr = [],[]
for alpha in alpha_range:
    reg = Ridge(alpha=alpha)
    linear = LinearRegression()
    regs = cross_val_score(reg,x,y,cv=5,scoring='r2').mean()
    linears = cross_val_score(linear,x,y,cv=5,scoring="r2").mean()
    ridge.append(regs)
    lr.append(linears)
plt.plot(alpha_range,ridge,c='red',label='Ridge')
plt.plot(alpha_range,lr,c='orange',label='LR')
plt.title('Mean')
plt.legend()
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

通过图形可以看出，线性回归处理的结果始终不变，但是岭回归处理的结果在alpha处于0-100时，有略微提升（不到0.001），但是随着alpha的进一步增大，R2指数大幅下降，但是总体下降也保持在0.006左右。所以，整体来看，加利佛尼亚房屋价值数据集存在轻微的多重共线性。

返回顶部

---

⑥ 细化学习曲线

• 由上一步得出的学习曲线可以看出在alpha处于0-200时，R2指数会有些上升，那么我们具体来看看。

# 细化学习曲线
alpha_range = np.arange(1,201,10)
ridge,lr = [],[]
for alpha in alpha_range:
    reg = Ridge(alpha=alpha)
    linear = LinearRegression()
    regs = cross_val_score(reg,x,y,cv=5,scoring='r2').mean()
    linears = cross_val_score(linear,x,y,cv=5,scoring="r2").mean()
    ridge.append(regs)
    lr.append(linears)
plt.plot(alpha_range,ridge,c='red',label='Ridge')
plt.plot(alpha_range,lr,c='orange',label='LR')
plt.title('Mean')
plt.legend()
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

• R2指数 ---- var（）

# 方差
alpha_range = np.arange(1,1001,100)
ridge,lr = [],[]
for alpha in alpha_range:
    reg = Ridge(alpha=alpha)
    linear = LinearRegression()
    regs = cross_val_score(reg,x,y,cv=5,scoring='r2').var()
    linears = cross_val_score(linear,x,y,cv=5,scoring="r2").var()
    ridge.append(regs)
    lr.append(linears)
plt.plot(alpha_range,ridge,c='red',label='Ridge')
plt.plot(alpha_range,lr,c='orange',label='LR')
plt.title('Mean')
plt.legend()
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

• 学习的目的是学到隐含在数据背后的规律，对具有同一规律的学习集以外的数据，经过训练的网络也能给出合适的输出，该能力称为泛化能力。
• 泛化误差反映了学习方法的泛化能力，如果一种方法学习的模型比另一种方法学习的模型具有更小的泛化误差，那么这种方法就是有效。事实上，泛化误差就是所学习到的模型的期望风险。
• 泛化误差 = 偏差 + 方差 + 噪声
• 学习算法的预测误差, 或者说泛化误差(generalization error)可以分解为三个部分: 偏差(bias), 方差(variance) 和噪声(noise). 在估计学习算法性能的过程中, 我们主要关注偏差与方差. 因为噪声属于不可约减的误差 (irreducible error).
• 1、偏差表示学习算法的期望预测与测试集标签的偏离程度，即刻画了学习算法本身的拟合能力。训练模型越复杂，则偏差越小，如线性回归可以通过增加参数个数来提高模型的复杂度，神经网络可以通过增加隐单元个数来提高模型的复杂度。
• 2、方差表示同样大小的训练数据集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响。若模型处于过拟合状态，不同训练数据集产生的学习模型相差较大。
• 3、噪声表示任何学习模型所能达到期望泛化误差的下界，即刻画了学习问题本身的难度。若噪声比较大，即使是最优模型，泛化误差也比较大。

通过描绘方差图可以看出，随着alpha越来越大，方差也是急速上升；相同，结合均值的急速下降来看，模型的泛化能力是在不断下降的。结合R2的原理来看，其实R2表现的就是捕获了的信息量，也就在某种程度上体现了模型的偏差情况，由上图看出R2均值急剧下降，可以说模型的偏差量逐渐变大，同时伴随着方差的不断变大。由此泛化误差逐渐变大，相对应的泛化能力逐渐下降。

参见大佬博文：机器学习中的泛化能力
参见大佬博文：泛化误差分解——偏差与方差

返回顶部

---

案例：波士顿房价

① R2指数 ---- mean（）

# 1.加载数据集
boston_data = load_boston()
x = pd.DataFrame(boston_data.data)
y = boston_data.target
x.columns = boston_data.feature_names

# 2.划分训练集、测试集
xtrain,xtest,ytrain,ytest = train_test_split(x,y,test_size=0.3,random_state=420)
for i in [xtrain,xtest]:
    i.index = range(i.shape[0])

# 3.训练岭回归模型
reg = Ridge(alpha=1).fit(xtrain,ytrain)
# 3.1 R2指数
r2_score = reg.score(xtest,ytest) # 0.7504796922136654

# 4.探索交叉验证下不同alpha，岭回归与线性回归的结果变化
alpha_range = np.arange(1,1001,100)
ridge,lr = [],[]
for alpha in alpha_range:
    reg = Ridge(alpha=alpha)
    linear = LinearRegression()
    regs = cross_val_score(reg,x,y,cv=5,scoring='r2').mean()
    linears = cross_val_score(linear,x,y,cv=5,scoring='r2').mean()
    ridge.append(regs)
    lr.append(linears)
plt.plot(alpha_range,ridge,c='red',label='Ridge')
plt.plot(alpha_range,lr,c='orange',label='LR')
plt.title('Mean')
plt.legend()
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

同样的我们对波士顿房价数据集进行模型训练，并且探索交叉验证下不同的alpha对于岭回归和线性回归的影响。通过图形可以看出，在alpha处于0-200左右的时候，R2指数均值明显上升，也就是说模型对于数据上的信息量捕捉较多，偏差较小；在200之后有所下降并且幅度较大（约在0.03）。相比于加利福尼亚数据集的表现，较为明显。

返回顶部

---

• 细化R2指数 ---- mean（）

alpha_range = np.arange(100,301,10)
ridge,lr = [],[]
for alpha in alpha_range:
    reg = Ridge(alpha=alpha)
    #linear = LinearRegression()
    regs = cross_val_score(reg,x,y,cv=5,scoring='r2').mean()
    #linears = cross_val_score(linear,x,y,cv=5,scoring='r2').mean()
    ridge.append(regs)
    lr.append(linears)
plt.plot(alpha_range,ridge,c='red',label='Ridge')
#plt.plot(alpha_range,lr,c='orange',label='LR')
plt.title('Mean')
plt.legend()
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14

这里进行细化的时候，需要将线性回归部分去掉，因为线性回归相对来说保持不变，并且数值较低，与岭回归相距太远，这样一来岭回归的图示效果不明显，如下图一。

在进行进一步处理后，得出了如下的图，在alpha处于大约175的时候可以取到R2指数的最大值。

• 注意

m = []
for i in range(100,300,10):
    # 3.训练岭回归模型
    reg = Ridge(alpha=i).fit(xtrain,ytrain)
    # 3.1 R2指数
    r2_score = reg.score(xtest,ytest) # 0.7504796922136654
    m.append(r2_score)
[0.7323071414013687, 0.7308298647680634, 0.7294076830146169, 0.7280399168133551, 0.7267248945259315, 0.7254603886919283,
 0.7242438916975088, 0.7230727895192606, 0.7219444701456151, 0.7208563898020044, 0.7198061117958099, 0.7187913275830451, 
 0.7178098663372833, 0.716859697157614, 0.7159389266530864, 0.7150457937188373, 0.714178662706431, 0.7133360157813282, 
 0.7125164449852812, 0.7117186443361565]    
1
2
3
4
5
6
7
8
9
10
11

本人将alpha的取值定义在了100-300之间，也就是上面部分的图形展示，按照道理来讲在这一段区间方差急剧降低，R2指数上升，偏差降低，那么泛化误差应该适当的小才对。但是这里求出的R2却在不断 的减小，原因可能是当alpha很大的时候，挤占了w中由原始的特征矩阵贡献的空间,因此a如果太大,也会导致w的估计出现较大的偏移,无法正确拟合数据的真实面貌。我们在使用中,需要找出a让模型效果变好的最佳取值。

返回顶部

---

② R2指数 ---- var()

alpha_range = np.arange(1,1001,100)
ridge,lr = [],[]
for alpha in alpha_range:
    reg = Ridge(alpha=alpha)
    linear = LinearRegression()
    regs = cross_val_score(reg,x,y,cv=5,scoring='r2').var()
    linears = cross_val_score(linear,x,y,cv=5,scoring='r2').var()
    ridge.append(regs)
    lr.append(linears)
plt.plot(alpha_range,ridge,c='red',label='Ridge')
plt.plot(alpha_range,lr,c='orange',label='LR')
plt.title('Var')
plt.legend()
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14

通过描绘方差的变化图来看，随着alpha的逐渐变大，数据集的方差是急剧减小的，模型逐渐趋于稳定。

通过整体的分析，比起加利福尼亚房屋价值数据集，波士顿房价数据集的方差明显降低，偏差也明显降低，可见使用岭回归是起到一定的作用的，模型泛化的能力是有可能会上升的。

返回顶部

---