BFS:解决拓扑排序问题

什么是拓扑排序？

要知道什么拓扑排序我们首先要知道什么是有向无环图，有向无环图我们看名字其实就很容易理解，有向就是有方向，无环就是没有环形结构，这里我们展示一下有向无环图和有向有环图：

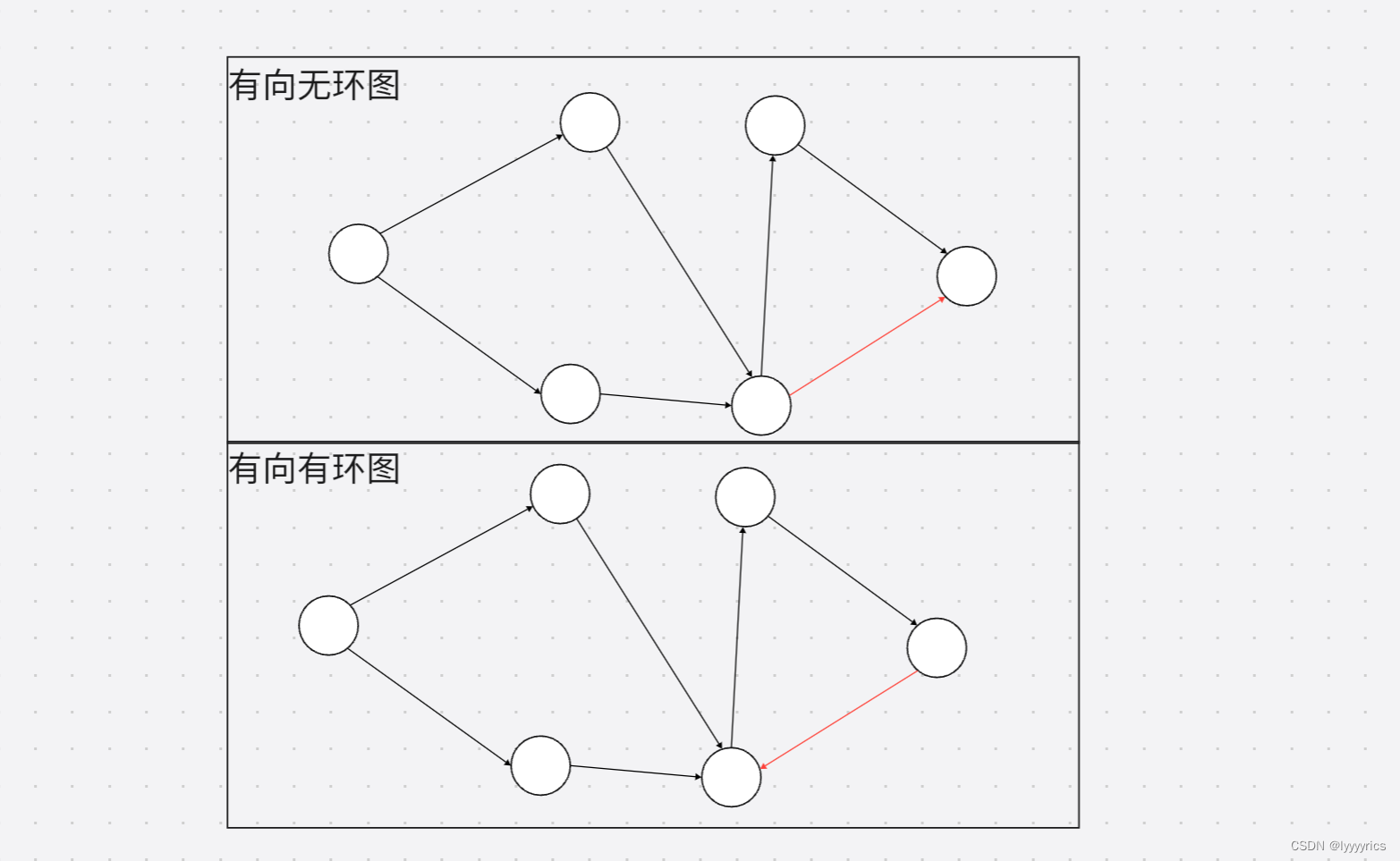
可以看见我们改变了一个边的方向，这个图就产生了环，接下来我们来介绍一下有向图中的一些专业术语：
入度（Indegree）：一个顶点的入度是指有多少条边指向这个顶点。换句话说，它表示该顶点有多少个直接前驱节点。（简单来说就是对于一个顶点来说，所有指向他的边之和）

出度（Outdegree）：一个顶点的出度是指从这个顶点出发有多少条边。也就是说，它表示该顶点有多少个直接后继节点。（简单来说对于一个顶点来说，，这个顶点往外伸出的边的总和）

接下来我们来说说AOV网，也就是顶点活动图。
在图论和调度问题中，AOV（Activity On Vertex）网是一个非常重要的概念。AOV网通常表示一组活动及其之间的依赖关系，特别适用于项目管理、任务调度和依赖分析等领域。在AOV网中，活动被表示为顶点，依赖关系被表示为有向边。这种结构使得我们可以通过拓扑排序等算法来有效地处理和分析活动的先后顺序。
最后我们再来说说拓扑排序，，简单介绍了上面的概念之后，拓扑排序就相当简单了，拓扑排序就是先将入度为零的顶点删除列出来，，并且将入度为0的连接的边删除。

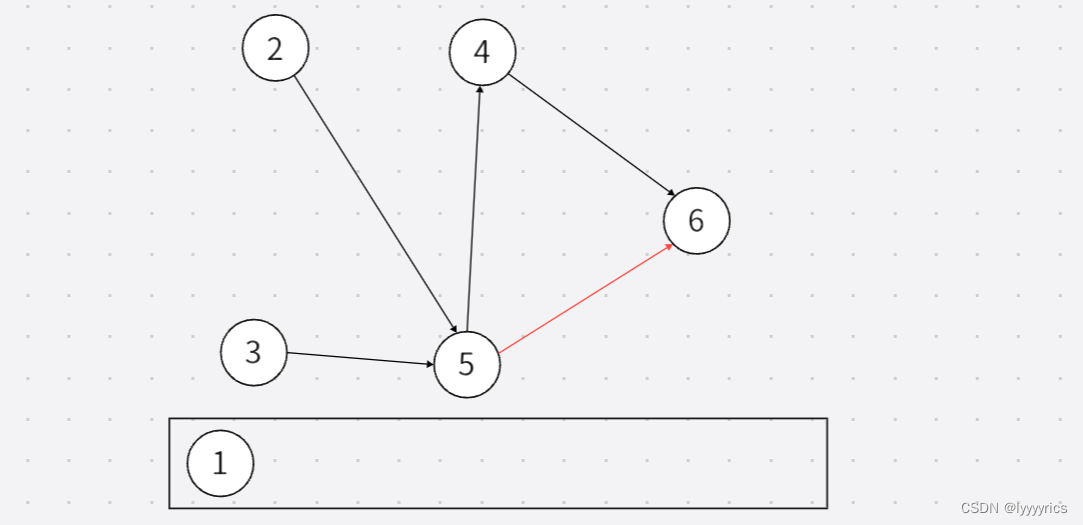
删除之后，，再将删除了的剩下的图中的入度为零的取出来，但是这里取出来的方法有两种，所以拓扑排序的 结果也不止一种。

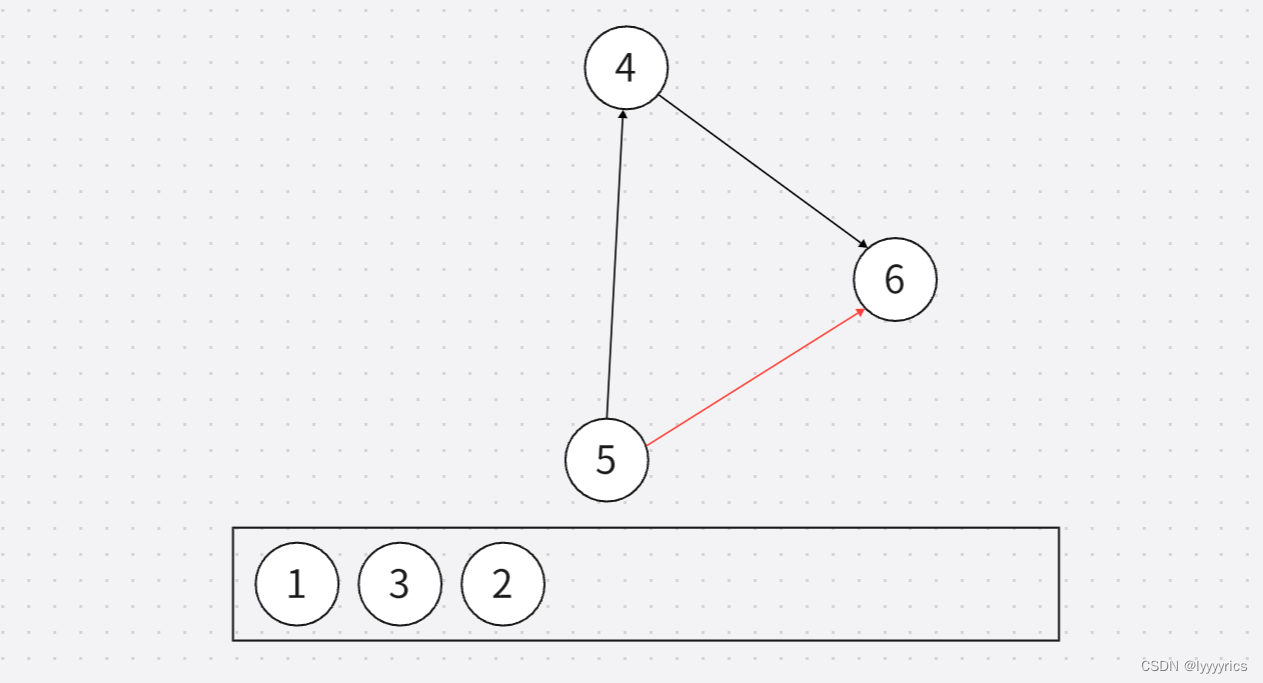
接下来我们就只能取5了，然后就是取4和6。

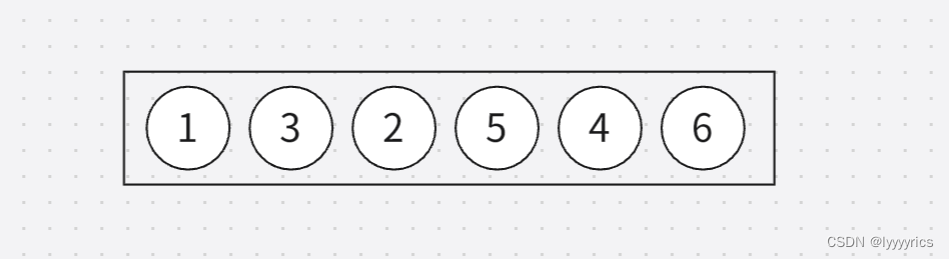
这不是唯一的拓扑排序的结果。
接下来我们来坐坐拓扑排序的问题

关于拓扑排序的题

1.课程表

题目链接
题目：

样例输出和输入：

这道题的意思很简单，这道题首先给我们numCourse个课程，我们要把给出的课程全部选修完，但是这个课程不是随便选修的，我们不能想选哪门选哪门，后面给出了一个数组，

这个数组给出了选修课的对应关系，我们要修b这门课程就得先把b这门课程先修完，这么说有点抽象，我们来看个例子。

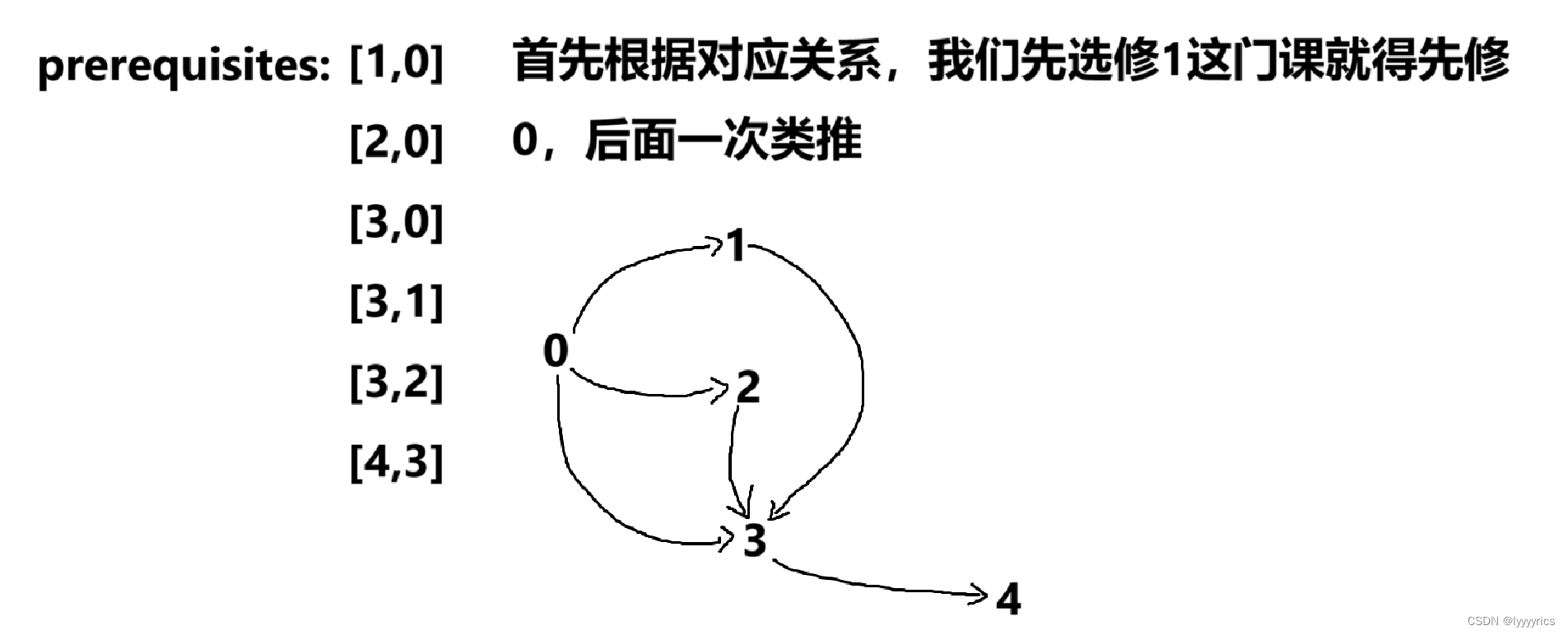
根据上面这个例子就可以推出这个关系，这不是直接转换为我们的拓扑排序了吗，这道题本质就是判断这个图有没有环，如果无环就返回true，如果有环就返回false。
算法原理：
上面算法原理基本已经讲完了，我们来看看代码如何书写，顺便再讲一点，这里我们要用拓扑排序问题又来了，我们是不是要建一个图，这里有涉及到该如何建图，这里我们讲一种方法，用邻接表建图，邻接表是什么呢？

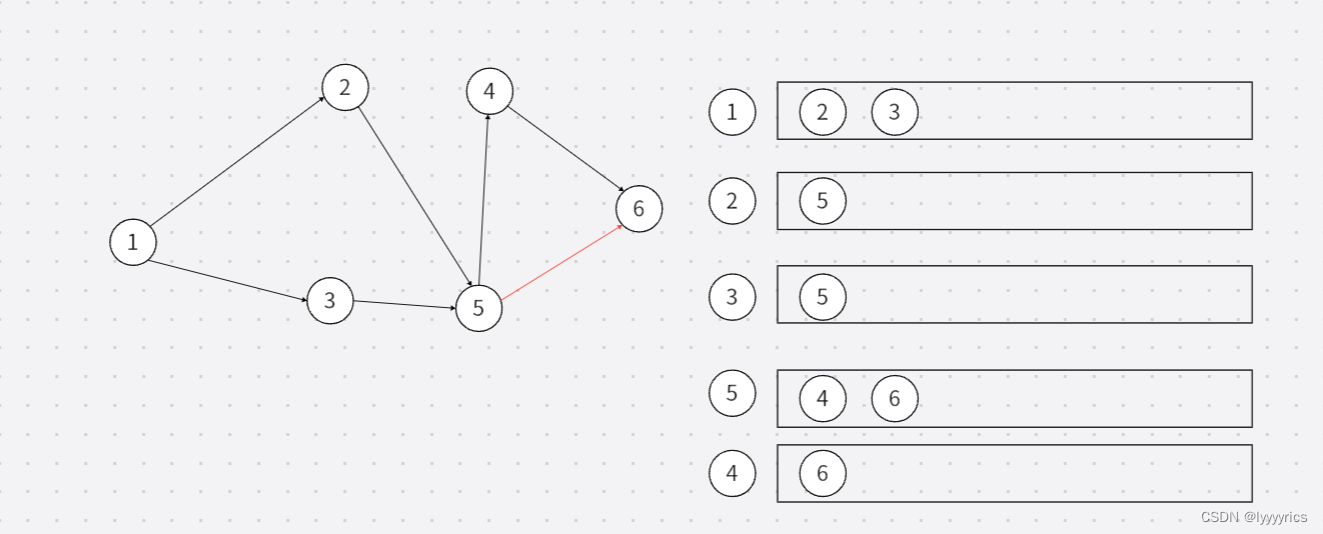
这大致就是邻接表，我们可以用一个顶点去索引这个节点指向的一系列节点，那么邻接表该如何实现呢？
邻接表一般的实现方法有：
1.unordered_map<int,vector<>>
2.vector<vector<>>
第一种实现方法用法很广泛，但是第二种实现方法很局限

代码展示：

class Solution {
public:
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
    //准备工作
    unordered_map<int, vector<int>> edges;//邻接表存储图
    vector<int> in(numCourses);//用来标记每个顶点的入度

    //建图
    for (auto e : prerequisites)
    {
        //先找到对应关系，b去映射a，是b指向a
        int a = e[0], b = e[1];
        //有一个b指向a的一条边
        edges[b].push_back(a);//在b这个节点后面插入a
        in[a]++;
    }

    //拓扑排序
    queue<int> q;
    //将所有入度为零的点添加到队列中
    for (int i = 0;i < numCourses;i++)
    {
        //如果当前节点的入度为0，直接入队列
        if (in[i] == 0)
        {
            q.push(i);
        }
    }

    //来一次BFS
    while (q.size())
    {
        int t = q.front();
        q.pop();
        //如果这道题是求最终
        for (auto e : edges[t])
        {
            in[e]--;
            if (in[e] == 0)q.push(e);
        }
    }
    for (int i = 0;i < numCourses;i++)
    {
        if (in[i] != 0)
        {
            return false;
        }
    }
    return true;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

运行结果：

2.课程表Ⅱ

题目链接
题目：

样例输出和输入：

这道题和第一道题几乎一模一样，但是问法上有些许差异，上道题让我们判断，但是这道题让我们返回结果，返回拓扑排序之后的那个数组，我们这里如果能拓扑排序则返回数组，如果不能则返回空的数组。

算法原理：
我们再BFS的时候每次BFS往内部往容器内插入数据即可。
代码展示：

class Solution {
public:
    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        unordered_map<int,vector<int>> edges;
        vector<int> in(numCourses);
        vector<int> anwser;
        //先建图
        for(auto e:prerequisites)
        {
            int a=e[0],b=e[1];
            edges[b].push_back(a);
            in[a]++;
        }

        queue<int> q;
        //拓扑排序
        for(int i=0;i<numCourses;i++)
        {
            //如果入度为零则直接返回
            if(in[i]==0)
            {
                q.push(i);
            }
        }

        while(q.size())
        {
            int t=q.front();
            q.pop();
            anwser.push_back(t);
            for(auto e:edges[t])
            {
                in[e]--;
                if(in[e]==0)
                {
                    q.push(e);
                }
            }
        }
        for(int i=0;i<numCourses;i++)
        {
            if(in[i])
            {
                return vector<int>();
            }
        }
        return anwser;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

运行结果：

3.火星词典

题目链接
题目：

样例输出和输入：

这道题就有点难了，我们首先要搞定题意，首先在我们印象里的字典序就是比如比较abc和abf这链各个字符串进行字典序比较，很显然后面的字典序大于前面的字典序，这是地球上的规则，但是上面给出了一个火星上的规则，所以在火星上，字典序可能和地球上不一样，这道题就是让我们求火星上的字典序排序，首先它先给出了一个words单词列表，这个单词列表是已经排好序的每个单词，这道题让我们返回的是给出的每个字符的字典序的大小的排序，从大到小，如果比较不出来就返回空字符串，这里我们给出 一个简单例子：

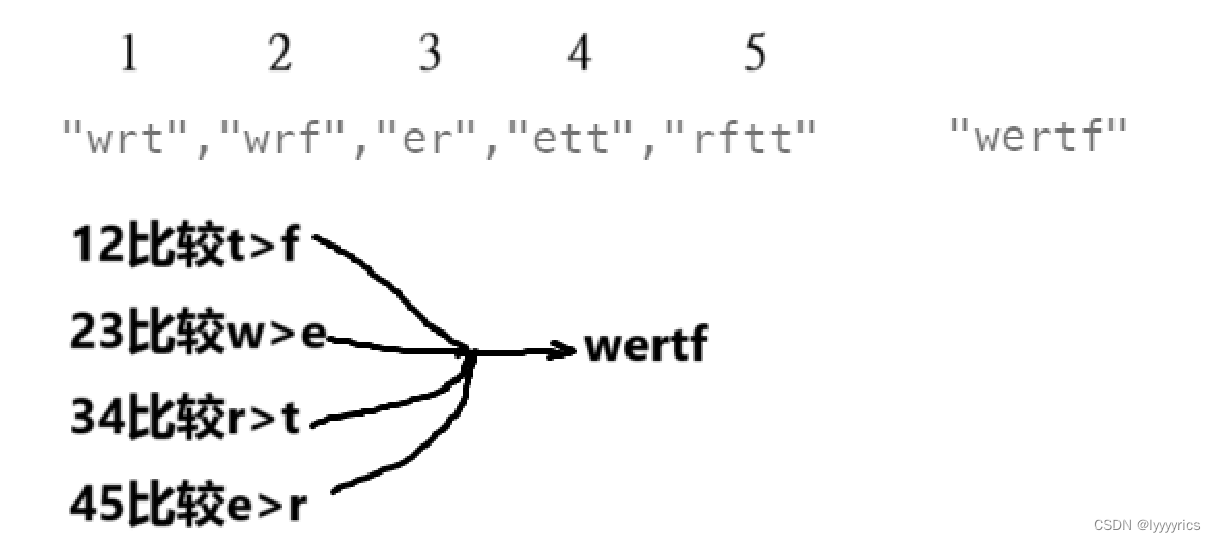
OK，搞懂题意了，我们来讲解算法原理

算法原理：

这道题其实也隐藏着拓扑排序，首先我们来看比较，这个比较就存在先后顺序，没有比w大的，所以没有指向w的，有比e大的所有指向e的，我们根据上面的比较关系来建立一个图：

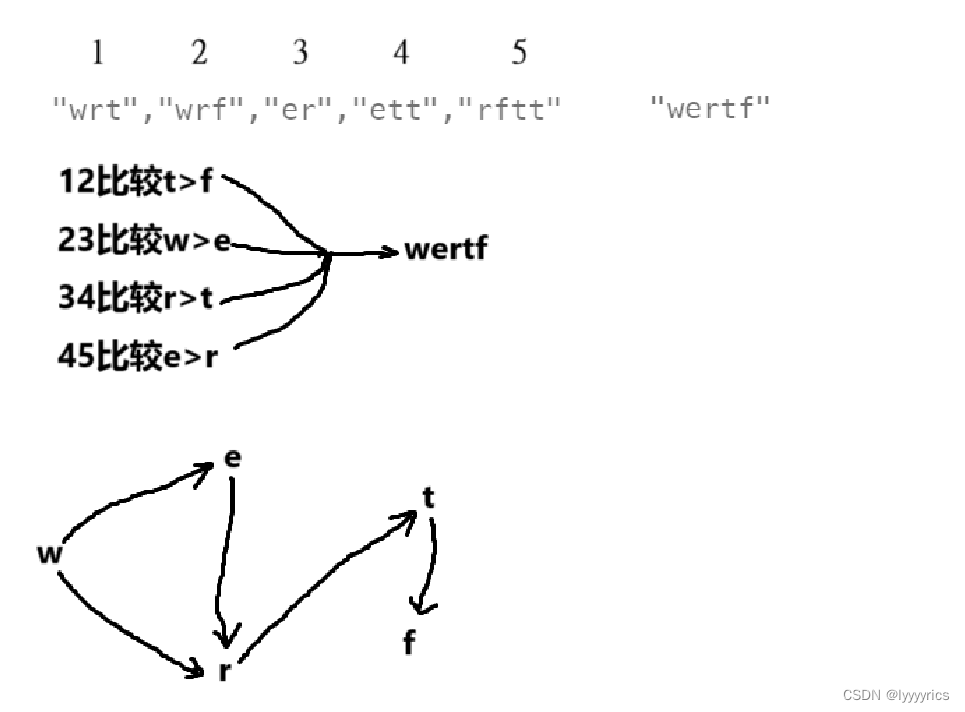
经过我们每次的比较，我们得到的字母的大小关系建立的图就是上面这个，然后进行拓扑排序：

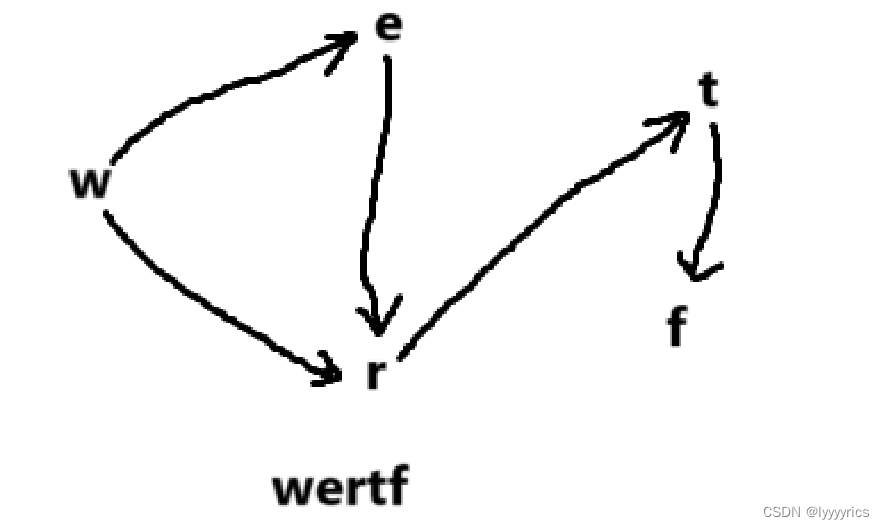
代码展示：

class Solution 
{
public:
    unordered_map<char,unordered_set<char>> edges;//储存图
    unordered_map<char,int> in;//统计入度
    bool check;//处理边界情况
    string alienOrder(vector<string>& words) 
    {
        //建图+初始化入度hash表
        int m=words.size();
        for(auto s:words)
        {
            for(auto ch:s)
            {
                in[ch]=0;
            }
        }
        for(int i=0;i<m;i++)
        {
            for(int j=i+1;j<m;j++)
            {
                add(words[i],words[j]);
                if(check==true)
                {
                    return "";
                }
            }
        }

        queue<char> q;
        for(auto &[a,b]:in)
        {
            if(b==0)q.push(a);
        }
        string ret;
        while(q.size())
        {
            char t=q.front();
            q.pop();
            ret+=t;
            for(auto e:edges[t])
            {
                in[e]--;
                if(in[e]==0)q.push(e);
            }
        }
        for(auto &[a,b]:in)
        {
            if(b)return "";
        }
        return ret;
    }
    void add(string& a,string& b)
    {
        int n=min(a.size(),b.size());
        int i=0;
        for(;i<n;i++)
        {
            if(a[i]!=b[i])
            {
                char s1=a[i],s2=b[i];//a->b;
                if(!edges.count(s1)||!edges[s1].count(s2))
                {
                    edges[s1].insert(s2);
                    in[s2]++;
                }
                break;
            }
        }
        if(i==b.size()&&i<a.size())check=true;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72

运行结果：

总结

在本文中，我们详细探讨了广度优先搜索（BFS）在解决拓扑排序问题中的应用。从拓扑排序的定义和基本概念出发，我们介绍了其在有向无环图（DAG）中的重要性。通过一步步剖析 BFS 算法的实现过程，我们展示了如何利用 BFS 有效地生成拓扑排序，并解决实际中的复杂问题。

在实现拓扑排序的过程中，BFS 提供了一种直观且高效的解决方案。通过维护一个入度数组和一个队列，BFS 能够准确地找到没有前驱节点的顶点，并逐步扩展到整个图。这种方法不仅易于理解和实现，而且在时间复杂度和空间复杂度上都表现优异，能够处理规模较大的图结构。

总结而言，广度优先搜索为拓扑排序提供了一种强大而灵活的工具。在面对各种复杂的依赖关系和任务调度问题时，BFS 的应用不仅能够确保结果的正确性，还能显著提升计算效率。希望通过本文的讲解，读者能够深入理解 BFS 在拓扑排序中的应用原理，并能够在实际编程中灵活运用这一算法，解决各类相关问题。未来，我们可以继续探索其他算法在拓扑排序中的应用，以及如何优化和扩展这些算法，以应对更复杂的实际需求。