游戏开发者怎么做出以假乱真的画面效果？大气散射渲染了解一下_大气散射怎么影响ambient

参与介质（Participating media）

参与介质是另一种现实中常见的介质，这种介质中粒子分散在一定体积内，比如烟雾、云、牛奶、大气等。

相比于一般的固体材质，光在这类材质中会传播一段较长的距离，因此不能用双向反射分布函数（BRDF）来描述光的传播。

1.1 参与介质的传播特性

光在参与介质中的传播主要有四个部分。

第一个是参与介质中的粒子本身会吸收光能，转换成其他形式的能量，这样在传播路径上的光就会衰减。

第二种是出散射，也就是散射，说的是光遇到粒子时，粒子会分散光的传播方向，因此也会减弱传播路径上的光。

第三种是粒子本身是发光的，这会加强传播路径上的光。

最后一种是入散射，其实本质上跟出散射是一个东西，也是粒子对光的散射，但入散射是指从其他传播路径上散射到当前传播路径上的现象，这会加强当前路径上的光的能量。
 

 

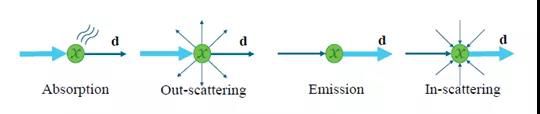
这四种现象就是光在参与介质中传播时视觉表现的基础。

下面的表展示了参与介质四种传播特性相对于的参数。
 

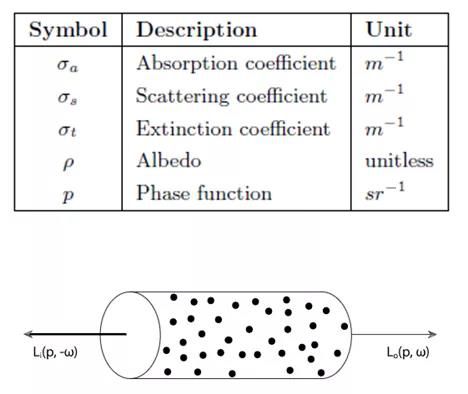
1.2 相位函数（Phase Function）

相位函数是用于描述粒子散射的分布函数。

因为当粒子散射光的时候，在各个方向上，散射的能量是不一样的，而且不同的粒子这个散射分布也不一样，所以，我们需要一个函数来描述这种分布。

通过相位函数我们可以得到这个方向上散射的光能占比.粒子的散射其实是个比较复杂的过程，而且与粒子大小和光波波长之间的比例关系是有关的，按照这个大小关系，可以分为三类散射。
 

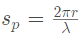
 ,rr为粒子半径，\lambdaλ为波长。

当 

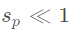
 ，为瑞利散射（Rayleigh scattering）。

当 

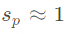
 ，为米氏散射（Mie scattering）。

当 

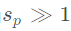
 ，为几何散射（Geometric scattering）。

1.3 瑞利散射（Rayleigh scattering）

瑞利散射的phase function可以用这个方程来描述：
 

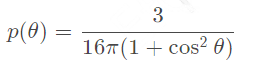
从下图中可以看出瑞利散射相对来说，方向性没有那么强。
 

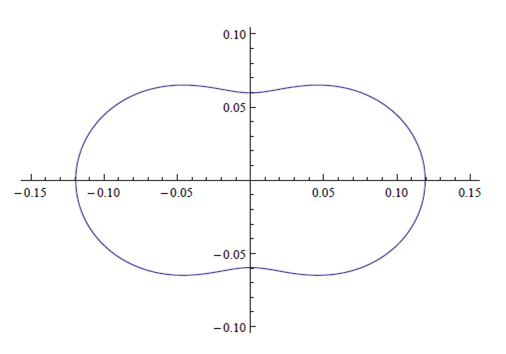
但瑞利散射的散射系数与光波的波长有很大的关系，这也是我们的地球大气呈现出色彩变化的原因，主要就是瑞利散射的光波相关性导致的。

1.4 米氏散射（Mie scattering）

相比瑞利散射，米氏散射就具有很强的方向性。

米氏散射方程比较复杂，一般实际中会用其他一些简化的方程代替，其中Henyey-Greenstein，简称HG方程就是比较常用的。
 

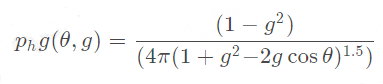
HG方程会有一个参数g用于控制散射的分布形状，当g小于0时，散射更多的是逆向的，等于0的时候是各向同性的，也就是在各个方向上散射的光能量是相等的，如果大于0就表示光更多的能量会向前传播。

还有另外一个常用的Schlick近似。
 

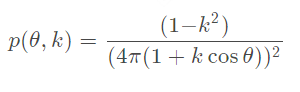
这个方程的计算量更小，但是当g比较大的时候近似值会偏离较大。

另一个，米氏散射的特点，就是相比于瑞利散射，光波对散射的影响没有那么大。

1.5 几何散射（Geometric scattering）

第三种常见散射是几何散射，这种散射主要关注那些粒子远大于光波的情况
因为粒子比较大，因此需要考虑光在粒子表面的反射与折射现象。

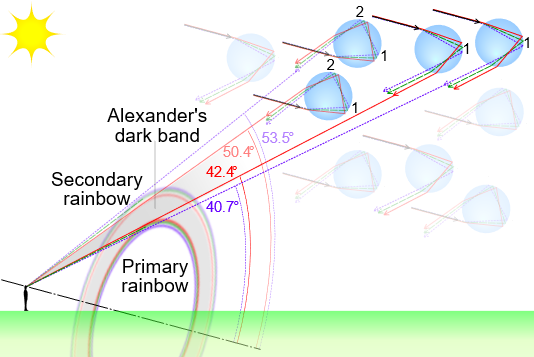
一个现实中常见的现象就是彩虹的形成，因为空气中散布着大尺寸的水粒子，当光照射的时候，会在水粒子表面以及内部发生折射。

由于不同波长的光的折射系数也是不同的，因此产生了色散的想象，也就形成了彩虹。

大气散射（Atmosphere Scattering）

地球大气的渲染主要包含两种散射，瑞利散射以及米氏散射，瑞利散射主要构成了天空的颜色变化，而米氏散射则造成了太阳周围的光环效果。
 

2.1 大气瑞利散射参数:
 

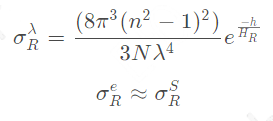
 表示散射系数， 

 表示衰减系数。
h表示海拔。
HR表示大气密度衰减系数。
n表示大气的折射系数。
N表示海平面的粒子密度。

2.2 大气米氏散射参数:
 

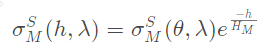
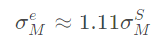
 表示散射系数， 

 表示衰减系数。
h表示海拔。
HM表示大气密度衰减系数。
 

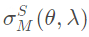
 表示海平面的米氏散射系数。

2.3 臭氧层吸收

另一个容易忽视的效应是臭氧层吸收对于大气散射效果的影响。

具体的实现方案也很简单，就是调整瑞利散射的吸收系数。

可以看到，尤其在太阳接近地平线的时候，天空的色彩会有比较明显的差异。
 

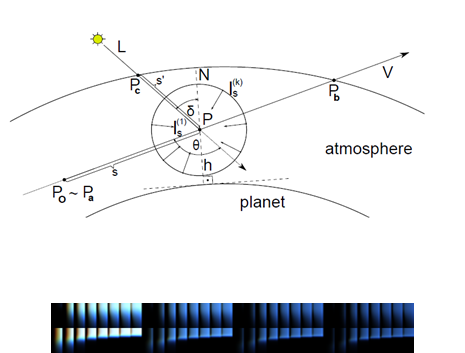
2.4 单次散射（Single Scattering）

单次散射公式如下：
 

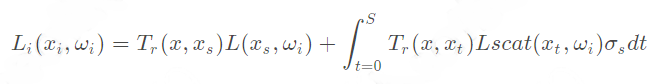
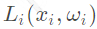
 表示到达视点的入射光。
 

 表示透过率（Transmittance）， 

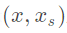
 表示之间累积的光照衰减。
 

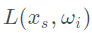
 表示物体表面光照。
 

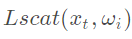
 表示散射光。

散射光的计算公式如下：
 

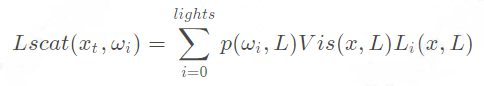
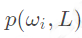
 表示相位函数。
 

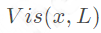
 表示可见性，阴影。
 

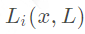
 表示到达采样点xx的光照。

透过率公式如下：
 

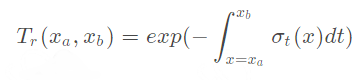
 称为光学深度（Optical depth）。

2.5 多重散射（Multi-Scattering）

前面我们看到了单次散射的计算过程，有单次与之相对的就有多重散射，多重散射的概念也很简单，多重散射就是经过多次散射然后到达视点。
 

多重散射的计算可以通过多次迭代实现，也就是用前一次散射的结果作为下一重散射的光源。

图中，可以看出，上面的是单次散射的结果，下面的是多重散射的结果，还是可以比较明显能看出区别的。
 

2.6 常见方案

现在我们已经知道散射是如何计算了，有公式之后，如果我们不考虑性能，通过蒙特卡洛积分法暴力求解的方式，就可以求得结果。

但很显然，实时计算的话，QQ靓号购买这种方式计算量就太大了，下面我们就看下目前常见的一些方案。

第一种就是靠美术同学预制一些天空的纹理贴图，然后通过插值的方式达到一定程度的动态性，这种方案比较大的问题就是如果要做比较复杂的动态会比较难，因为当我们的影响因子越多，意味着预制的贴图数量会指数级增加。

第二种就是公式拟合[PSS99] [HW12] [CIE94]，这种方式就是通过一个公式去直接计算大气散射的结果，这种方案也缺乏一定的可定制性。

第三种也是公式拟合的思路，但是与第二种不一样的是，这种拟合只会拟合计算中的一部分。

其中最出名，应用比较广泛的应该就是GPU Gems中的算法，作者通过公式拟合了光学深度的计算，从而使得透射率可以通过公式直接求解。这样就可以对积分公式进行降维，单次散射就只需要计算一重积分，这样的话实时计算性能也是可以接收的。但这种方案相对来说效果上还是与ground truth会有一定差距，而且如果我们考虑多重散射的话，即便是通过拟合减少了一重积分，计算量依然是很大的[ONeil05] [Schüler12]。

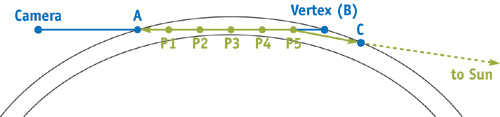
最后一种方案，是预计算的方案[Ril04] [Wen07] [Yus15] [Brun08] [Elek09]，通过预计算积分结果，存储在LUT中，然后实时通过采样LUT获得结果，这种方案也是目前PC以及主机上最主流的方案。

这种方案的优势就是效果是非常好的，因为是离线的计算，因此可以做到非常接近ground truth，比如多重散射，在这种方案中非常方便的就可以实现，而且没有额外的实时性能开销。

但是预计算通常最大的问题就是参数维度太多导致预计算的数据量会太大，不过通过业界大佬们的努力，以及可以将预计算的参数维度降到3维，另外通过将相位函数这种高频信息剥离到实时计算。

可以进一步减少LUT的分辨率，使得预计算的数据变得很小。

具体的算法其实并不复杂，最终，只需要通过海拔、太阳的照射角度、以及视角这三个参数预计算大气散射的结果就可以了。

另外相位函数会被从积分中提出来，然后实时去计算，和采样的LUT结合计算最终的结果。
 

大气散射与高度雾（Height Fog）

高度雾也是目前非常常见的雾效方案，一般计算的方式就是通过解析式计算雾的光学深度得到透射率，然后blend一个雾的颜色。

但是如果我们从前面的散射公式去看这种计算的话，我们会发现，直接混合雾的颜色其实是对散射光一个简化。

如果我们希望获得更好的效果，很显然我们需要一个更接近ground truth的版本，所以我们需要用当前的光照环境带入到高度雾的计算中。

这里我们主要的参考就是decima在17年siggraph上的分享。
 

下面是他们的具体做法，其实公式非常简单，就是一个alpha blend，也就是之前我们的高度雾是blend一个颜色，这里改成blend Lsun加Lamb。

而这里的Lsun就是太阳的直接光经过雾效衰减后的结果，Lambient是大气散射结果经过雾效衰减后的结果，这两个结果也会通过预计算的方式存储在LUT中。
 

下图是sponza场景中的效果，上图是原始的高度雾，Blend一个纯色，下图是结合了大气散射的效果，可以看出右侧的雾效会更有光感。
 

References：


[Brun08] Bruneton, Eric, and Fabrice Neyret. “Precomputed atmospheric scattering.” Computer graphics forum. Vol. 27. No. 4. Oxford, UK: Blackwell Publishing Ltd, 2008.
[CIE94] AC08352780, Anonymus, ed. “Spatial distribution of daylight-luminance distributions of various reference skies.” CIE, 1994.
[Elek09] Elek, Oskar. “Rendering parametrizable planetary atmospheres with multiple scattering in real-time.” Proceedings of the Central European Seminar on Computer Graphics. Citeseer, 2009.
[Giliam17] “Decima Engine: Advances in Lighting and AA.” SIGGRAPH 2017 Conference. 2017.
[Hill16] Hillaire, Sbastien. “Physically based sky, atmosphere and cloud rendering in frostbite.” ACM SIGGRAPH. 2016.
[HW12] Hosek, Lukas, and Alexander Wilkie. “An analytic model for full spectral sky-dome radiance.” ACM Transactions on Graphics (TOG) 31.4 (2012): 1-9.
[ONeil05] O’Neil, Sean. “Accurate atmospheric scattering.” Gpu Gems 2 (2005): 253-268.
[Ril04] Riley, Kirk, et al. “Efficient rendering of atmospheric phenomena.” Rendering Techniques 4 (2004): 374-386.
[PSS99] Preetham, Arcot J., Peter Shirley, and Brian Smits. “A practical analytic model for daylight.” Proceedings of the 26th annual conference on Computer graphics and interactive techniques. 1999.
[Sébas20] Sébastien Hillaire. “A Scalable and Production Ready Sky and Atmosphere Rendering Technique”. Eurographics Symposium on Rendering. 2020.
[Schüler12] Schüler, Christian. “An approximation to the chapman grazing-incidence function for atmospheric scattering.” GPU PRO 3: Advanced Rendering Techniques (2012): 105.
[Wen07] Wenzel, Carsten. “Real-Time atmospheric effects in games revisited.” Game Developers Conference. 2007.
[Yus15] Yusov, Egor. “Outdoor light scattering sample update.” URL: https://software. intel. com/en-us/blogs/2013/09/19/otdoor-lightscattering-sample-update (2015).