Operations Research课程之非线性规划（梯度下降｜牛顿法｜Gurobi+Python）_gurobi求解非线性规划

目录

1.非线性规划介绍

2.梯度下降法(Gradient descent)

2.1 梯度和Hessians矩阵

2.2 梯度下降算法

2.3 算法举例

3. 牛顿法(Newton’s method)

3.1 适合单变量的牛顿法

3.2 适合多变量的牛顿法

3. 实例(Gurobi+Python)

3.1 Agricultural Pricing问题描述

3.2 Gurobi+Python代码

---

来源：Coursera课程Operations Research (2): Optimization Algorithms Week4

课程前言：

怎么求解一个有数千个变量和约束的问题？为什么求解整数规划比线性规划需要更多时间？为什么线性化很重要，为什么不直接把问题建模成非线性规划模型？

（1）精确解

• 线性规划：单纯形法
• 整数规划：分枝定界
• 非线性规划✅：梯度下降和牛顿法

（2）启发式解

很多场景下建立数学模型再调用求解器是不够的，现实问题非常复杂，我们还需要为特定的问题设计特定的算法，许多情况下会使用启发式算法，能在合理的时间内找到近似最优

1.非线性规划介绍

很多现实的工程问题都是非线性的，需要依赖数值算法获得一个数值解，非线性规划（NLP）算法通常有以下步骤：

• 迭代（Iterative）：算法会在某次迭代中移动到一个点，然后从这个点开始下一次迭代
• 重复（Repetitive）：每次迭代会重复一些步骤
• 贪婪（Greedy）：每次迭代会寻找当前迭代轮次中最好的那个
• 近似（Approximation）：依赖原始问题的一阶或二阶近似

NLP算法有一些难点：

• NLP算法可能无法收敛： 如果更多的迭代不能改进修正当前解，算法会收敛至这个解，有些情况下算法也会根本无法收敛
• NLP算法可能陷入局部最优：迭代开始点非常重要，算法会采取一些方法得到多个局部解
• NLP算法需要域是连续且连通的：非线性整数规划比较难求解

下面介绍两种简单的NLP算法：梯度下降和牛顿法，主要求解无约束非线性优化问题，对于带约束的优化问题，需要结合使用其它方法，如拉格朗日乘子，罚函数，序列二次规划，内点法等。

2.梯度下降法(Gradient descent)

2.1 梯度和Hessians矩阵

举例说明计算过程：

 梯度是一个N维向量，可以通过朝着这个方向移动来改善当前解，梯度是最快的上升方向

2.2 梯度下降算法

由于梯度是上升方向，对于最小化问题需要沿着其反方向移动，给定一个当前解，在每次迭代更新公式为，其中a>0，称为步长（step size），和深度学习里的学习率概念类似，当前解的梯度为0时停止迭代。怎么选择合适的步长？一个不合适的步长可能会导致算法不收敛，以下面的为例

为了找到最合适的步长，需要在每次梯度更新前引入一个子问题：最大程度的改进（largest improvement)，即沿着当前方向能到达的最优的点

梯度下降的每次迭代没有局限在可行域，可能会跳出可行域然后移动回来，搜索速度会更快

2.3 算法举例

以包含两个变量的函数为例，下面是迭代两次的过程，在求解步长时，由于自变量已知，因此子问题只有步长一个变量，便于求解。

3. 牛顿法(Newton’s method)

梯度下降法是一种一阶方法，比较直观，但是有时会比较慢，牛顿法依赖二阶梯度（Hessians矩阵）来求解，速度更快。

3.1 适合单变量的牛顿法

 以EOQ库存控制模型为例说明过程

3.2 适合多变量的牛顿法

与单变量牛顿法一样，只是梯度从单变量梯度变成了Hessians矩阵，每次迭代更新向量如下：

 对于牛顿法：

• 牛顿法没有梯度下降法中的步长
• 对于二次函数，能在一次迭代中就找到最优解
• 在某些情况下比梯度下降法更快
• 对于某些函数也会难以收敛，比如非凸函数
• 梯度下降的单次迭代一定是更好的方法，而牛顿法取决于函数性质

还有一些更通性的问题：

• 收敛保证
• 收敛速度
• 不可导函数
• 约束优化

3. 实例(Gurobi+Python)

3.1 Agricultural Pricing问题描述

来自Gurobi官方案例：Agricultural Pricing​​​​​​​

agricultural pricing problem农产品定价问题：确定一个国家乳制品的价格和需求，以便最大限度地提高这些产品销售的总收入。使用 Gurobi Python API 将此问题建模为二次优化问题，并使用 Gurobi 优化器解决它，二次规划（Quadratic Programming QP）是非线性规划问题的一个特例。Gurobi对于LP问题使用单纯刑法和内点法求解，这些算法经过扩展也能用于求解QP问题。

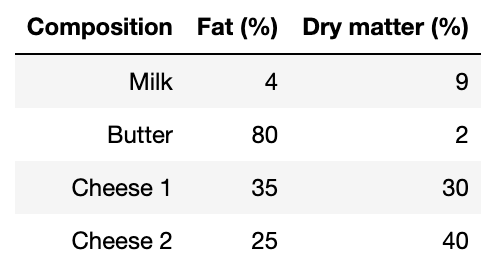
一个国家的政府想要决定其乳制品的价格，这些产品都是（直接或间接）由该国的原奶生产企业生产的。 原奶有两个主要成分：脂肪和干物质。 减去用于出口或农场消费的脂肪和干物质的数量后，每年的脂肪可用总量为 60 万吨，干物质可用总量为 75 万吨， 这些都可用于生产供国内消费的乳制品（牛奶、黄油和两种奶酪），4种产品组成百分比如下表所示：

下表显示了去年国内乳制品消费（需求）和价格：

弹性和交叉弹性如下表所示，弹性（elasticities）是指同一产品价格变动导致消费量变动的程度，交叉弹性（cross-elasticities）是指产品A的价格变动导致产品B的消费量变动的程度。这样基于去年国内乳制品消费（需求）和价格，能对今年决策的消费和价格进行约束限制。

价格指数不能高于去年，去年的价格指数是1.939（以千美元计），规定限制新价格必须保证去年消费的总成本不会增加，这样基于去年国内乳制品消费（需求）能对今年决策的价格进行约束限制。优化目标是确定今年的价格和消费（需求）量可以使总收入最大化。模型如下：

3.2 Gurobi+Python代码

和求解MIP问题代码类似，但是要设置模型参数，模型按照求解MIP的逻辑来求解此类非凸问题

model.params.nonConvex = 2
Continuous model is non-convex -- solving as a MIP

 模型数据：

import gurobipy as gp
from gurobipy import GRB
 
dairy = ['milk', 'butter', 'cheese1', 'cheese2']
components = ['fat', 'dryMatter']
components, capacity = gp.multidict({
    ('fat'):600,
    ('dryMatter'):750})
cd, qtyper = gp.multidict({
    ('fat','milk'): 0.04,
    ('fat','butter'): 0.8,
    ('fat','cheese1'): 0.35,
    ('fat','cheese2'): 0.25,
    ('dryMatter','milk'): 0.09,
    ('dryMatter','butter'): 0.02,
    ('dryMatter','cheese1'): 0.3,
    ('dryMatter','cheese2'): 0.4})
dairy, consumption, price, elasticity = gp.multidict({
    ('milk'): [4.82, 0.297, 0.4],
    ('butter'): [0.32, 0.72, 2.7],
    ('cheese1'): [0.21, 1.05, 1.1],
    ('cheese2'): [0.07, 0.815, 0.4]})
priceIndex = 1.939
elasticity12 = 0.1
elasticity21 = 0.4

代码核心： 

model = gp.Model()
model.params.nonConvex = 2
 
# 决策变量：价格和消费量
newp = model.addVars(dairy, name="new price")
newc = model.addVars(dairy, name="new consumption")
 
# 目标函数：最大化收入
model.setObjective(newp.prod(newc), GRB.MAXIMIZE)
 
# 约束条件
#（1）成分总量约束
model.addConstrs((gp.quicksum(qtyper[c,d]*newc[d] for d in dairy)) <= capacity[c] 
                 for c in components)
 
#（2）价格指数约束
model.addConstr((gp.quicksum(consumption[d]*newp[d] for d in dairy)) <= priceIndex)
 
#（3）弹性系数约束
model.addConstr((newc['milk']-consumption['milk'])/consumption['milk']
                ==-elasticity['milk']*((newp['milk']-price['milk'])/price['milk']))
 
model.addConstr((newc['butter']-consumption['butter'])/consumption['butter']
                ==-elasticity['butter']*((newp['butter']-price['butter'])/price['butter']))
 
model.addConstr((newc['cheese1']-consumption['cheese1'])/consumption['cheese1']
                ==-elasticity['cheese1']*((newp['cheese1']-price['cheese1'])/price['cheese1'])
                +elasticity12*((newp['cheese2']-price['cheese2'])/price['cheese2']))
 
model.addConstr((newc['cheese2']-consumption['cheese2'])/consumption['cheese2']
                ==-elasticity['cheese2']*((newp['cheese2']-price['cheese2'])/price['cheese2'])
                +elasticity21*((newp['cheese1']-price['cheese1'])/price['cheese1']))
 
model.optimize()

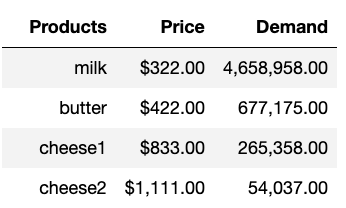
 运行结果

Solution count 6: 2.06641 2.06641 2.06641 ... 2.04229
 
Optimal solution found (tolerance 1.00e-04)
Best objective 2.066407962090e+00, best bound 2.066408976227e+00, gap 0.0000%

结果展示： 

import pandas as pd
price_demand = pd.DataFrame(columns=["Products", "Price", "Demand"])
for d in dairy:
    price_demand = price_demand._append({"Products": d, 
                                        "Price": '${:,.2f}'.format(round(1000*newp[d].x)), 
                                        "Demand": '{:,.2f}'.format(round(1e6*newc[d].x))}, 
                                        ignore_index=True)  
price_demand.index=[''] * len(price_demand)
price_demand