深度学习入门，keras实现回归模型_keras回归模型

Regression with Keras

在本教程中，您将学习如何使用 Keras 和深度学习执行回归。 您将学习如何训练 Keras 神经网络进行回归和连续值预测，特别是在房价预测的背景下。

今天的帖子开始了关于深度学习、回归和连续值预测的 3 部分系列。

我们将在房价预测的背景下研究 Keras 回归预测：

第 1 部分：今天我们将训练 Keras 神经网络，以根据分类和数字属性（例如卧室/浴室的数量、平方英尺、邮政编码等）来预测房价。

第 2 部分：下周我们将训练 Keras 卷积神经网络，以根据房屋本身的输入图像（即房屋、卧室、浴室和厨房的正面视图）预测房价。

第 3 部分：在两周内，我们将定义和训练一个神经网络，该网络将我们的分类/数字属性与我们的图像相结合，从而比单独使用属性或图像进行更好、更准确的房价预测。

与分类（预测标签）不同，回归使我们能够预测连续值。

例如，分类可能能够预测以下值之一：{便宜、负担得起、昂贵}。

另一方面，回归将能够预测确切的美元金额，例如“这所房子的估计价格为 489,121 美元”。

在许多实际情况中，例如房价预测或股票市场预测，应用回归而不是分类对于获得良好的预测至关重要。

要学习如何使用 Keras 执行回归，请继续阅读！

在本教程的第一部分，我们将简要讨论分类和回归之间的区别。

然后，我们将探索用于本系列 Keras 回归教程的房价数据集。 从那里，我们将配置我们的开发环境并审查我们的项目结构。

在此过程中，我们将学习如何使用 Pandas 加载我们的房价数据集并定义一个用于 Keras 回归预测的神经网络。

最后，我们将训练我们的 Keras 网络，然后评估回归结果。

分类与回归

图 1：分类网络预测标签（顶部）。 相比之下，回归网络可以预测数值（底部）。 在这篇博文中，我们将使用 Keras 对房屋数据集进行回归。

通常，我们会在分类的背景下讨论 Keras 和深度学习——预测标签以表征图像或输入数据集的内容。 另一方面，回归使我们能够预测连续值。 让我们再次考虑房价预测的任务。 众所周知，分类用于预测类标签。 对于房价预测，我们可以将分类标签定义为：

labels = {very cheap, cheap, affordable, expensive, very expensive}
1

如果我们进行分类，我们的模型就可以学习根据一组输入特征预测这五个值中的一个。

然而，这些标签仅代表房屋的潜在价格范围，但不代表房屋的实际成本。

为了预测房屋的实际成本，我们需要进行回归。

使用回归，我们可以训练模型来预测连续值。 例如，虽然分类可能只能预测一个标签，但回归可以说： “根据我输入的数据，我估计这所房子的成本为 781,993 美元。” 上面的图 1 提供了执行分类和回归的可视化。 在本教程的其余部分，您将学习如何使用 Keras 训练神经网络进行回归。

房价数据集

我们今天将使用的数据集来自 2016 年的论文，Ahmed 和 Moustafa 撰写的基于视觉和文本特征的房价估计。 该数据集包括数值/分类属性以及 535 个数据点的图像，使其成为研究回归和混合数据预测的绝佳数据集。 房屋数据集包括四个数值和分类属性：

• 卧室数量
• 浴室数量
• 面积（即平方英尺）
• 邮政编码

这些属性以 CSV 格式存储在磁盘上。 在本教程的后面，我们将使用 pandas（一种用于数据分析的流行 Python 包）从磁盘加载这些属性。 每个房子还提供了总共四张图片：

• 卧室
• 浴室
• 厨房
• 房子的正面图

房屋数据集的最终目标是预测房屋本身的价格。

环境配置

对于这个由 3 部分组成的系列博客文章，您需要安装以下软件包：

• NumPy
• sklearn-learn
• pandas
• Keras
• OpenCV（用于本系列的下两篇博文）

下载数据集

$ git clone https://github.com/emanhamed/Houses-dataset
1

如果有git，则用git下载，没有直接打开网页链接下载。

项目结构

$ tree --dirsfirst --filelimit 10
.
├── Houses-dataset
│   ├── Houses Dataset [2141 entries]
│   └── README.md
├── model
│   ├── __init__.py
│   ├── datasets.py
│   └── models.py
└── mlp_regression.py

1
2
3
4
5
6
7
8
9
10
11

datasets.py ：我们用于从数据集中加载数值/分类数据的脚本

models.py：神经网络模型 今天将审查这两个脚本。 此外，我们将在接下来的两个教程中重用 datasets.py 和 models.py（经过修改），以保持我们的代码有条理和可重用。

回归 + Keras 脚本包含在 mlp_regression.py 中，我们也将对其进行讲解。

加载房价数据集

在我们训练 Keras 回归模型之前，我们首先需要加载房屋数据集的数值和分类数据。 打开 datasets.py 文件并插入以下代码：

# import the necessary packages
from sklearn.preprocessing import LabelBinarizer
from sklearn.preprocessing import MinMaxScaler
import pandas as pd
import numpy as np
import glob
import cv2
import os
def load_house_attributes(inputPath):
	# initialize the list of column names in the CSV file and then
	# load it using Pandas
	cols = ["bedrooms", "bathrooms", "area", "zipcode", "price"]
	df = pd.read_csv(inputPath, sep=" ", header=None, names=cols)
1
2
3
4
5
6
7
8
9
10
11
12
13

我们首先从 scikit-learn、pandas、NumPy 和 OpenCV 导入库和模块。 接下来将使用 OpenCV，因为我们将向该脚本添加加载图像的功能。 定义了 load_house_attributes 函数，它接受输入数据集的路径。 在函数内部，我们首先定义 CSV 文件中列的名称。 从那里，我们使用 pandas 的函数 read_csv 将 CSV 文件作为第 14 行的日期框架 (df) 加载到内存中。 下面你可以看到我们输入数据的一个例子，包括卧室数量、浴室数量、面积（即平方英尺）、邮政编码、代码，最后是我们的模型应该训练来预测的目标价格：

 bedrooms  bathrooms  area  zipcode     price
0         4        4.0  4053    85255  869500.0
1         4        3.0  3343    36372  865200.0
2         3        4.0  3923    85266  889000.0
3         5        5.0  4022    85262  910000.0
4         3        4.0  4116    85266  971226.0
1
2
3
4
5
6

让我们完成 load_house_attributes 函数的其余部分：

    # determine (1) the unique zip codes and (2) the number of data
	# points with each zip code
	zipcodes = df["zipcode"].value_counts().keys().tolist()
	counts = df["zipcode"].value_counts().tolist()
	# loop over each of the unique zip codes and their corresponding
	# count
	for (zipcode, count) in zip(zipcodes, counts):
		# the zip code counts for our housing dataset is *extremely*
		# unbalanced (some only having 1 or 2 houses per zip code)
		# so let's sanitize our data by removing any houses with less
		# than 25 houses per zip code
		if count < 25:
			idxs = df[df["zipcode"] == zipcode].index
			df.drop(idxs, inplace=True)
	# return the data frame
	return df
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

在剩下的几行中，我们：

• 确定唯一的邮政编码集，然后计算每个唯一邮政编码的数据点数。
• 过滤掉计数低的邮政编码。 对于某些邮政编码，我们只有一两个数据点，这使得获得准确的房价估算即使并非不可能，也极具挑战性。
• 将数据返回给调用函数。

现在让我们创建用于预处理数据的 process_house_attributes 函数：

def process_house_attributes(df, train, test):
	# initialize the column names of the continuous data
	continuous = ["bedrooms", "bathrooms", "area"]
	# performin min-max scaling each continuous feature column to
	# the range [0, 1]
	cs = MinMaxScaler()
	trainContinuous = cs.fit_transform(train[continuous])
	testContinuous = cs.transform(test[continuous])
1
2
3
4
5
6
7
8

我们定义函数。 process_house_attributes 函数接受三个参数：

• df ：pandas 生成的我们的数据框（前面的函数帮助我们从数据框中删除一些记录）
• train ：我们针对房价数据集的训练数据
• test ：我们的测试数据。

然后，我们定义了连续数据的列，包括卧室、浴室和房屋大小。

我们将采用这些值并使用 sklearn-learn 的 MinMaxScaler 将连续特征缩放到范围 [0, 1]。 现在我们需要预处理我们的分类特征，即邮政编码：

    # one-hot encode the zip code categorical data (by definition of
	# one-hot encoing, all output features are now in the range [0, 1])
	zipBinarizer = LabelBinarizer().fit(df["zipcode"])
	trainCategorical = zipBinarizer.transform(train["zipcode"])
	testCategorical = zipBinarizer.transform(test["zipcode"])
	# construct our training and testing data points by concatenating
	# the categorical features with the continuous features
	trainX = np.hstack([trainCategorical, trainContinuous])
	testX = np.hstack([testCategorical, testContinuous])
	# return the concatenated training and testing data
	return (trainX, testX)
1
2
3
4
5
6
7
8
9
10
11

首先，我们将对邮政编码进行one-hot编码。

然后，我们将使用 NumPy 的 hstack 函数将分类特征与连续特征连接起来，将生成的训练和测试集作为元组返回。 请记住，现在我们的分类特征和连续特征都在 [0, 1] 范围内。

实现回归神经网络

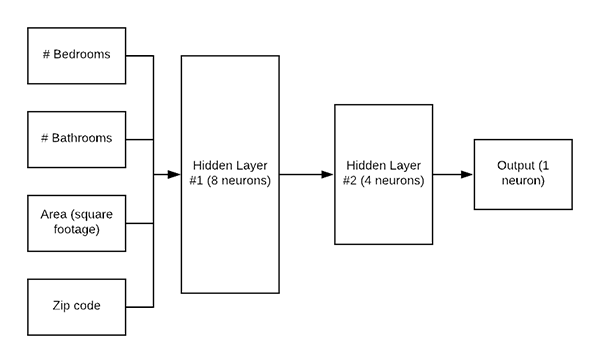
图 5：我们的 Keras 回归架构。 网络的输入是一个数据点，包括家庭的#卧室、#浴室、面积/平方英尺和邮政编码。 网络的输出是具有线性激活函数的单个神经元。 线性激活允许神经元输出房屋的预测价格。

在我们训练 Keras 网络进行回归之前，我们首先需要定义架构本身。 今天我们将使用一个简单的多层感知器 (MLP)，如图 5 所示。 打开models.py文件并插入以下代码：

# import the necessary packages
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import BatchNormalization
from tensorflow.keras.layers import Conv2D
from tensorflow.keras.layers import MaxPooling2D
from tensorflow.keras.layers import Activation
from tensorflow.keras.layers import Dropout
from tensorflow.keras.layers import Dense
from tensorflow.keras.layers import Flatten
from tensorflow.keras.layers import Input
from tensorflow.keras.models import Model
def create_mlp(dim, regress=False):
	# define our MLP network
	model = Sequential()
	model.add(Dense(8, input_dim=dim, activation="relu"))
	model.add(Dense(4, activation="relu"))
	# check to see if the regression node should be added
	if regress:
		model.add(Dense(1, activation="linear"))
	# return our model
	return model
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

首先，我们将从 Keras 导入所有必要的模块。通过编写一个名为 create_mlp 的函数来定义 MLP 架构。 该函数接受两个参数： dim : 定义我们的输入维度 regress : 一个布尔值，定义是否应该添加我们的回归神经元 我们将继续使用dim-8-4架构开始构建我们的MLP。 如果我们正在执行回归，我们会添加一个 Dense 层，其中包含一个具有线性激活函数的神经元。 通常我们使用基于 ReLU 的激活，但由于我们正在执行回归，我们需要一个线性激活。 最后，返回模型。

实现Keras 回归脚本

现在是时候把所有的部分放在一起了！

打开 mlp_regression.py 文件并插入以下代码：

# import the necessary packages
from tensorflow.keras.optimizers import Adam
from sklearn.model_selection import train_test_split
from pyimagesearch import datasets
from pyimagesearch import models
import numpy as np
import argparse
import locale
import os
# construct the argument parser and parse the arguments
ap = argparse.ArgumentParser()
ap.add_argument("-d", "--dataset", type=str, required=True,
	help="path to input dataset of house images")
args = vars(ap.parse_args())
1
2
3
4
5
6
7
8
9
10
11
12
13
14

我们首先导入必要的包、模块和库。

我们的脚本只需要一个命令行参数 --dataset。 当您在终端中运行训练脚本时，您需要提供 --dataset 开关和数据集的实际路径。

让我们加载房屋数据集属性并构建我们的训练和测试分割：

# construct the path to the input .txt file that contains information
# on each house in the dataset and then load the dataset
print("[INFO] loading house attributes...")
inputPath = os.path.sep.join([args["dataset"], "HousesInfo.txt"])
df = datasets.load_house_attributes(inputPath)
# construct a training and testing split with 75% of the data used
# for training and the remaining 25% for evaluation
print("[INFO] constructing training/testing split...")
(train, test) = train_test_split(df, test_size=0.25, random_state=42)
1
2
3
4
5
6
7
8
9

使用我们方便的 load_house_attributes 函数，并通过将 inputPath 传递给数据集本身，我们的数据被加载到内存中。

训练集和测试集按照4：1切分。 让我们扩展我们的房价数据：

# find the largest house price in the training set and use it to
# scale our house prices to the range [0, 1] (this will lead to
# better training and convergence)
maxPrice = train["price"].max()
trainY = train["price"] / maxPrice
testY = test["price"] / maxPrice
1
2
3
4
5
6

如评论中所述，将我们的房价缩放到 [0, 1] 范围将使我们的模型更容易训练和收敛。 将输出目标缩放到 [0, 1] 将减少我们的输出预测范围（相对于 [0, maxPrice ]），不仅使我们的网络训练更容易、更快，而且使我们的模型能够获得更好的结果。 因此，我们获取训练集中的最高价格，并相应地扩展我们的训练和测试数据。 现在让我们处理房屋属性：

# process the house attributes data by performing min-max scaling
# on continuous features, one-hot encoding on categorical features,
# and then finally concatenating them together
print("[INFO] processing data...")
(trainX, testX) = datasets.process_house_attributes(df, train, test)
1
2
3
4
5

从 datasets.py 脚本中回忆 process_house_attributes 函数：

• 预处理我们的分类和连续特征。
• 通过最小-最大缩放将我们的连续特征缩放到范围 [0, 1]。
• One-hot 编码我们的分类特征。
• 连接分类特征和连续特征以形成最终特征向量。

现在让我们继续训练MLP模型：

# create our MLP and then compile the model using mean absolute
# percentage error as our loss, implying that we seek to minimize
# the absolute percentage difference between our price *predictions*
# and the *actual prices*
model = models.create_mlp(trainX.shape[1], regress=True)
opt = Adam(lr=1e-3, decay=1e-3 / 200)
model.compile(loss="mean_absolute_percentage_error", optimizer=opt)
# train the model
print("[INFO] training model...")
model.fit(x=trainX, y=trainY, 
	validation_data=(testX, testY),
	epochs=200, batch_size=8)
1
2
3
4
5
6
7
8
9
10
11
12

我们的模型用 Adam 优化器初始化，然后compile。 请注意，我们使用平均绝对百分比误差作为我们的损失函数，这表明我们寻求最小化预测价格和实际价格之间的平均百分比差异。

训练。

训练完成后，我们可以评估我们的模型并总结我们的结果：

# make predictions on the testing data
print("[INFO] predicting house prices...")
preds = model.predict(testX)
# compute the difference between the *predicted* house prices and the
# *actual* house prices, then compute the percentage difference and
# the absolute percentage difference
diff = preds.flatten() - testY
percentDiff = (diff / testY) * 100
absPercentDiff = np.abs(percentDiff)
# compute the mean and standard deviation of the absolute percentage
# difference
mean = np.mean(absPercentDiff)
std = np.std(absPercentDiff)
# finally, show some statistics on our model
locale.setlocale(locale.LC_ALL, "en_US.UTF-8")
print("[INFO] avg. house price: {}, std house price: {}".format(
	locale.currency(df["price"].mean(), grouping=True),
	locale.currency(df["price"].std(), grouping=True)))
print("[INFO] mean: {:.2f}%, std: {:.2f}%".format(mean, std))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

第 57 行指示 Keras 对我们的测试集进行预测。

使用预测，我们计算：

• 预测房价与实际房价之间的差异。
• 百分比差异。
• 绝对百分比差异。
• 计算绝对百分比差异的均值和标准差。
• 结果打印。

使用 Keras 进行回归并没有那么难，对吧？ 让我们训练模型并分析结果！

Keras 回归结果

图 6： Keras 回归模型采用四个数值输入，产生一个数值输出：房屋的预测值。

打开一个终端并提供以下命令（确保 --dataset 命令行参数指向您下载房价数据集的位置）：

$ python mlp_regression.py --dataset Houses-dataset/Houses\ Dataset/
[INFO] loading house attributes...
[INFO] constructing training/testing split...
[INFO] processing data...
[INFO] training model...
Epoch 1/200
34/34 [==============================] - 0s 4ms/step - loss: 73.0898 - val_loss: 63.0478
Epoch 2/200
34/34 [==============================] - 0s 2ms/step - loss: 58.0629 - val_loss: 56.4558
Epoch 3/200
34/34 [==============================] - 0s 1ms/step - loss: 51.0134 - val_loss: 50.1950
Epoch 4/200
34/34 [==============================] - 0s 1ms/step - loss: 47.3431 - val_loss: 47.6673
Epoch 5/200
34/34 [==============================] - 0s 1ms/step - loss: 45.5581 - val_loss: 44.9802
Epoch 6/200
34/34 [==============================] - 0s 1ms/step - loss: 42.4403 - val_loss: 41.0660
Epoch 7/200
34/34 [==============================] - 0s 1ms/step - loss: 39.5451 - val_loss: 34.4310
Epoch 8/200
34/34 [==============================] - 0s 2ms/step - loss: 34.5027 - val_loss: 27.2138
Epoch 9/200
34/34 [==============================] - 0s 2ms/step - loss: 28.4326 - val_loss: 25.1955
Epoch 10/200
34/34 [==============================] - 0s 2ms/step - loss: 28.3634 - val_loss: 25.7194
...
Epoch 195/200
34/34 [==============================] - 0s 2ms/step - loss: 20.3496 - val_loss: 22.2558
Epoch 196/200
34/34 [==============================] - 0s 2ms/step - loss: 20.4404 - val_loss: 22.3071
Epoch 197/200
34/34 [==============================] - 0s 2ms/step - loss: 20.0506 - val_loss: 21.8648
Epoch 198/200
34/34 [==============================] - 0s 2ms/step - loss: 20.6169 - val_loss: 21.5130
Epoch 199/200
34/34 [==============================] - 0s 2ms/step - loss: 19.9067 - val_loss: 21.5018
Epoch 200/200
34/34 [==============================] - 0s 2ms/step - loss: 19.9570 - val_loss: 22.7063
[INFO] predicting house prices...
[INFO] avg. house price: $533,388.27, std house price: $493,403.08
[INFO] mean: 22.71%, std: 18.26%
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

从我们的输出中可以看出，我们最初的平均绝对百分比误差高达 73%，然后迅速下降到 30% 以下。

当我们完成训练时，我们可以看到我们的网络开始有点过拟合了。 我们的训练损失低至~20%； 然而，我们的验证损失约为 23%。

计算我们最终的平均绝对百分比误差，我们得到的最终值为 22.71%。 这个值是什么意思？

我们最终的平均绝对百分比误差意味着，平均而言，我们的网络在其房价预测中将降低约 23%，标准差为约 18%。

房价数据集的局限性

在房价预测中获得 22% 的折扣是一个好的开始，但肯定不是我们正在寻找的准确性类型。 也就是说，这种预测准确性也可以看作是房价数据集本身的局限性。 请记住，数据集仅包含四个属性：

• 卧室数量
• 浴室数量
• 面积（即平方英尺）
• 邮政编码

大多数其他房价数据集包含更多属性。

例如，波士顿房价数据集包括总共 14 个可用于房价预测的属性（尽管该数据集确实存在一些种族歧视）。 Ames House 数据集包含超过 79 个不同的属性，可用于训练回归模型。 在本系列的下两篇文章中，我将向您展示如何： 将我们的数值/分类数据与房屋图像相结合，生成的模型优于我们之前所有的 Keras 回归实验。

总结

在本教程中，您学习了如何使用 Keras 深度学习库进行回归。 具体来说，我们使用 Keras 和回归根据四个数值和分类属性来预测房屋价格：

• 卧室数量
• 浴室数量
• 面积（即平方英尺）
• 邮政编码

总的来说，我们的神经网络获得了 22.71% 的平均绝对百分比误差，这意味着，平均而言，我们的房价预测将下降 22.71%。

代码和模型下载：
https://download.csdn.net/download/hhhhhhhhhhwwwwwwwwww/35595361