devbox
正经夜光杯
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

Python数模笔记-Sklearn（4）线性回归_线性回归 sklearn

作者：正经夜光杯 | 2024-07-15 15:10:33

赞

踩

线性回归 sklearn

1、什么是线性回归？

回归分析（Regression analysis)是一种统计分析方法，研究自变量和因变量之间的定量关系。回归分析不仅包括建立数学模型并估计模型参数，检验数学模型的可信度，也包括利用建立的模型和估计的模型参数进行预测或控制。按照输入输出变量关系的类型，回归分析可以分为线性回归和非线性回归。

线性回归（Linear regression） 假设样本数据集中的输出变量（y）与输入变量（X）存在线性关系，即输出变量是输入变量的线性组合。线性模型是最简单的模型，也是非常重要和应用广泛的模型。

如果模型只有一个输入变量和一个输出变量，称为一元线性模型，可以用一条直线来描述输出与输入的关系，其表达式是一元一次方程：

y = w0 + w1*x1 + e

如果模型包括两个或多个输入变量，则称为多元线性模型，可以用一个平面或超平面来描述输出与输入的关系，其表达式是多元一次方程：

Y = w0 + w1*x1 + w2*x2+…+ wm*xm + e

采用最小二乘法（Least square method）可以通过样本数据来估计回归模型的参数，使模型的输出与样本数据之间的误差平方和最小。

回归分析还要进一步分析究竟能不能采用线性回归模型，或者说线性关系的假设是否合理、线性模型是否具有良好的稳定性？这就需要使用统计分析进行显著性检验，检验输入与输出变量之间的线性关系是否显著，用线性模型来描述它们之间的关系是否恰当。


欢迎关注 Youcans 原创系列，每周更新数模笔记

Python数模笔记-PuLP库
Python数模笔记-StatsModels统计回归
Python数模笔记-Sklearn
Python数模笔记-NetworkX
Python数模笔记-模拟退火算法


2、SKlearn 中的线性回归方法（sklearn.linear_model）

以机器学习的角度来看，回归是广泛应用的预测建模方法，线性回归是机器学习中重要的基础算法。SKlearn 机器学习工具包提供了丰富的线性模型学习方法，最重要和应用最广泛的无疑是普通最小二乘法（Ordinary least squares，OLS），此外多项式回归（Polynomial regression）、逻辑回归（Logistic Regression）和岭回归（Ridge regression）也较为常用，将在本文及后续文中介绍。其它方法相对比较特殊，以下根据官网介绍给出简要说明，普通读者可以略过。

  1. 普通最小二乘法（Ordinary least squares）：
    以模型预测值与样本观测值的残差平方和最小作为优化目标。
  2. 岭回归（Ridge regression）
    在普通最小二乘法的基础上增加惩罚因子以减少共线性的影响，以带惩罚项（L2正则化）的残差平方和最小作为优化目标。在指标中同时考虑了较好的学习能力以及较小的惯性能量，以避免过拟合而导致模型泛化能力差。
  3. Lasso 回归（Least absolute shrinkage and selection operator）
    在普通最小二乘法的基础上增加绝对值偏差作为惩罚项（L1正则化）以减少共线性的影响，在拟合广义线性模型的同时进行变量筛选和复杂度调整，适用于稀疏系数模型。
  4. 多元 Lasso 回归（Multi-task Lasso）
    用于估计多元回归稀疏系数的线性模型。注意不是指多线程或多任务，而是指对多个输出变量筛选出相同的特征变量（也即回归系数整列为 0，因此该列对应的输入变量可以被删除）。
  5. 弹性网络回归（Elastic-Net）
    引入L1和L2范数正则化而构成带有两种惩罚项的模型，相当于岭回归和 Lasso 回归的组合。
  6. Multi-task Elastic-Net
    用于估计多元回归稀疏系数线性模型的弹性网络回归方法。
  7. 最小角回归算法（Least Angle Regression）
    结合前向梯度算法和前向选择算法，在保留前向梯度算法的精确性的同时简化迭代过程。每次选择都加入一个与相关度最高的自变量，最多 m步就可以完成求解。特别适合于特征维度远高于样本数的情况。
  8. LARS Lasso
    使用最小角回归算法求解 Lasso模型。
  9. 正交匹配追踪法（Orthogonal Matching Pursuit）
    用于具有非零系数变量数约束的近似线性模型。在分解的每一步进行正交化处理，选择删除与当前残差最大相关的列，反复迭代达到所需的稀疏程度。
  10. 贝叶斯回归（Bayesian Regression）
    用贝叶斯推断方法求解的线性回归模型，具有贝叶斯统计模型的基本性质，可以求解权重系数的概率密度函数。可以被用于观测数据较少但要求提供后验分布的问题，例如对物理常数的精确估计；也可以用于变量筛选和降维。
  11. 逻辑回归（Logistic Regression）
    逻辑回归是一种广义线性模型，研究顺序变量或属性变量作为输出的问题，实际是一种分类方法。通过线性模型加Sigmoid映射函数，将线性模型连续型输出变换为离散值。常用于估计某种事物的可能性，如寻找危险因素、预测发病概率、判断患病概率，是流行病学和医学中最常用的分析方法。
  12. 广义线性回归（Generalized Linear Regression）
    广义线性回归是线性回归模型的推广，实际上是非线性模型。通过单调可微的联结函数，建立输出变量与输入变量的线性关系，将问题简洁直接地转化为线性模型来处理。
  13. 随机梯度下降（Stochastic Gradient Descent）
    梯度下降是一种基于搜索的最优化方法，用梯度下降法来求损失函数最小时的参数估计值，适用样本数（和特征数）非常非常大的情况。随机梯度下降法在计算下降方向时，随机选一个数据进行计算，而不是扫描全部训练数据集，加快了迭代速度。
  14. 感知机（Perceptron）
    感知机是一种适合大规模学习的简单分类算法。训练速度比SGD稍快，并且产生的模型更稀疏。
  15. 被动攻击算法（Passive Aggressive Algorithms）
    被动攻击算法是一类用于大规模学习的算法。
  16. 鲁棒性回归（Robustness regression）
    鲁棒性回归的目的是在存在损坏数据的情况下拟合回归模型，如存在异常值或错误的情况。
  17. 多项式回归（Polynomial regression）
    多项式回归通过构造特征变量的多项式来扩展简单的线性回归模型。例如将特征变量组合成二阶多项式，可以将抛物面拟合到数据中，从而具有更广泛的灵活性和适应性。

3、SKlearn 中的最小二乘线性回归方法

3.1 最小二乘线性回归类（LinearRegression ）

SKlearn 包中的 LinearRegression() 方法，不宜从字面理解为线性回归方法， LinearRegression() 仅指基于普通最小二乘法（OLS）的线性回归方法。

sklearn.linear_model.LinearRegression 类是 OLS 线性回归算法的具体实现，官网介绍详见：https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html#sklearn.linear_model.LinearRegression

sklearn.linear_model.LinearRegression()

class sklearn.linear_model.LinearRegression(*, fit_intercept=True, normalize=False, copy_X=True, n_jobs=None, positive=False)

LinearRegression() 类的参数不多，通常几乎不需要设置。

  • fit_intercept：bool, default=True　　是否计算截距。默认值 True，计算截距。
  • normalize：bool, default=False　　是否进行数据标准化，该参数仅在 fit_intercept = True 时有效。
  • n_jobs：int, default=None　　 计算时设置的任务数，为 n>1和大规模问题提供加速。默认值 任务数为 1。

LinearRegression() 类的主要属性：

  • coef_： 　　线性系数，即模型参数 w1… 的估计值
  • intercept_：　　截距，即模型参数 w0 的估计值

LinearRegression() 类的主要方法：

  • fit(X,y[,sample_weight])　　用样本集（X, y）训练模型。sample_weight 为每个样本设权重，默认None。
  • get_params([deep])　　获取模型参数。注意不是指模型回归系数，而是指fit_intercept,normalize等参数。
  • predict(X)　　用训练的模型预测数据集 X 的输出。即可以对训练样本给出模型输出结果，也可以对测试样本给出预测结果。
  • score(X,y[,sample_weight])　　R2 判定系数，是常用的模型评价指标。
3.2 一元线性回归

LinearRegression 使用例程：

# skl_LinearR_v1a.py
# Demo of linear regression by scikit-learn
# Copyright 2021 YouCans, XUPT
# Crated：2021-05-12
#  -*- coding: utf-8 -*-

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error, median_absolute_error

# 生成测试数据:
nSample = 100
x = np.linspace(0, 10, nSample)  # 起点为 0，终点为 10，均分为 nSample个点
e = np.random.normal(size=len(x))  # 正态分布随机数
y = 2.36 + 1.58 * x + e  # y = b0 + b1*x1

# 按照模型要求进行数据转换：输入是 array类型的 n*m 矩阵，输出是 array类型的 n*1 数组
x = x.reshape(-1, 1)  # 输入转换为 n行 1列（多元回归则为多列）的二维数组
y = y.reshape(-1, 1)  # 输出转换为 n行1列的二维数组
# print(x.shape,y.shape)

# 一元线性回归：最小二乘法(OLS)
modelRegL = LinearRegression()  # 创建线性回归模型
modelRegL.fit(x, y)  # 模型训练：数据拟合
yFit = modelRegL.predict(x)  # 用回归模型来预测输出

# 输出回归结果
print('回归截距: w0={}'.format(modelRegL.intercept_))  # w0: 截距
print('回归系数: w1={}'.format(modelRegL.coef_))  # w1,..wm: 回归系数

# 回归模型的评价指标
print('R2 确定系数：{:.4f}'.format(modelRegL.score(x, y)))  # R2 判定系数
print('均方误差：{:.4f}'.format(mean_squared_error(y, yFit)))  # MSE 均方误差
print('平均绝对值误差：{:.4f}'.format(mean_absolute_error(y, yFit)))  # MAE 平均绝对误差
print('中位绝对值误差：{:.4f}'.format(median_absolute_error(y, yFit)))  # 中值绝对误差

# 绘图：原始数据点，拟合曲线
fig, ax = plt.subplots(figsize=(8, 6))
ax.plot(x, y, 'o', label="data")  # 原始数据
ax.plot(x, yFit, 'r-', label="OLS")  # 拟合数据

ax.legend(loc='best')  # 显示图例
plt.title('Linear regression by SKlearn (Youcans)')
plt.show()  # YouCans, XUPT
# = 关注 Youcans，分享原创系列 https://blog.csdn.net/youcans =

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46

程序说明：

  1. 线性回归模型 LinearRegression() 类在模型训练 modelRegL.fit(x, y) 时，要求输入 x 和输出 y 数据格式为 array类型的 n*m 矩阵。一元回归模型 m=1，也要转换为 n*1 的 array类型：
x = x.reshape(-1, 1)  # 输入转换为 n行 1列（多元回归则为多列）的二维数组
y = y.reshape(-1, 1)  # 输出转换为 n行1列的二维数组

  • 1
  • 2
  1. LinearRegression() 类提供的模型评价指标只有 R2指标，但在 sklearn.metrics 包中提供了均方误差、平均绝对值误差和中位绝对值误差，例程中给出了其使用方法。

程序运行结果：

回归截距: w0=[2.45152704]
回归系数: w1=[[1.57077698]]
R2 确定系数：0.9562
均方误差：0.9620
平均绝对值误差：0.7905
中位绝对值误差：0.6732

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
3.2 多元线性回归

用 LinearRegression() 解决多元线性回归问题与一元线性回归的步骤、参数和属性都是相同的，只是要注意样本数据的格式要求：输入数据 X 是 array 类型的 n*m 二维数组，输出数据 y 是 array类型的 n*1 数组（也可以用 n*k 表示多变量输出）。
　　
问题描述：
　　数据文件 toothpaste.csv 中收集了 30个月牙膏销售量、价格、广告费用及同期的市场均价。
　　（1）分析牙膏销售量与价格、广告投入之间的关系，建立数学模型；
　　（2）估计所建立数学模型的参数，进行统计分析；
　　（3）利用拟合模型，预测在不同价格和广告费用下的牙膏销售量。
　　需要说明的是，本文例程并不是问题最佳的求解方法和结果，只是使用该问题及数据示范读取数据文件和数据处理的方法。

LinearRegression 使用例程：

# skl_LinearR_v1b.py
# Demo of linear regression by scikit-learn
# v1.0d: 线性回归模型（SKlearn）求解
# Copyright 2021 YouCans, XUPT
# Crated：2021-05-12

#  -*- coding: utf-8 -*-
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, mean_absolute_error, median_absolute_error

# = 关注 Youcans，分享原创系列 https://blog.csdn.net/youcans =
# 主程序
def main():  # 主程序
    # 读取数据文件
    readPath = "../data/toothpaste.csv"  # 数据文件的地址和文件名
    dfOpenFile = pd.read_csv(readPath, header=0, sep=",")  # 间隔符为逗号，首行为标题行
    dfData = dfOpenFile.dropna()  # 删除含有缺失值的数据
    print(dfData.head())  # YouCans, XUPT

    # Model 1：Y = b0 + b1*X1 + b2*X2 + e
    # 线性回归：分析因变量 Y(sales) 与 自变量 x1(diffrence)、x2(advertise) 的关系
    # 按照模型要求进行数据转换：输入是 array类型的 n*m 矩阵，输出是 array类型的 n*1 数组
    feature_cols = ['difference', 'advertise']  # 创建特征列表
    X = dfData[feature_cols]  # 使用列表选择样本数据的特征子集
    y = dfData['sales']  # 选择样本数据的输出变量
    # print(type(X),type(y))
    # print(X.shape, y.shape)
    # 一元线性回归：最小二乘法(OLS)
    modelRegL = LinearRegression()  # 创建线性回归模型
    modelRegL.fit(X, y)  # 模型训练：数据拟合
    yFit = modelRegL.predict(X)  # 用回归模型来预测输出
    # 输出回归结果
    print("\nModel1: Y = b0 + b1*x1 + b2*x2")
    print('回归截距: w0={}'.format(modelRegL.intercept_))  # w0: 截距
    print('回归系数: w1={}'.format(modelRegL.coef_))  # w1,..wm: 回归系数
    # 回归模型的评价指标
    print('R2 确定系数：{:.4f}'.format(modelRegL.score(X, y)))  # R2 判定系数
    print('均方误差：{:.4f}'.format(mean_squared_error(y, yFit)))  # MSE 均方误差
    print('平均绝对值误差：{:.4f}'.format(mean_absolute_error(y, yFit)))  # MAE 平均绝对误差
    print('中位绝对值误差：{:.4f}'.format(median_absolute_error(y, yFit)))  # 中值绝对误差

    # Model 3：Y = b0 + b1*X1 + b2*X2 + b3*X2**2 + e
    # 线性回归：分析因变量 Y(sales) 与 自变量 x1、x2 及 x2平方的关系
    x1 = dfData['difference']  # 价格差，x4 = x1 - x2
    x2 = dfData['advertise']  # 广告费
    x5 = x2**2  # 广告费的二次元
    X = np.column_stack((x1,x2,x5))  # [x1,x2,x2**2]
    # 多元线性回归：最小二乘法(OLS)
    modelRegM = LinearRegression()  # 创建线性回归模型
    modelRegM.fit(X, y)  # 模型训练：数据拟合
    yFit = modelRegM.predict(X)  # 用回归模型来预测输出
    # 输出回归结果, YouCans
    print("\nModel3: Y = b0 + b1*x1 + b2*x2 + b3*x2**2")
    print('回归截距: w0={}'.format(modelRegM.intercept_))  # w0: 截距, YouCans
    print('回归系数: w1={}'.format(modelRegM.coef_))  # w1,..wm: 回归系数, XUPT
    # 回归模型的评价指标 ,XUPT
    print('R2 确定系数：{:.4f}'.format(modelRegM.score(X, y)))  # R2 判定系数
    print('均方误差：{:.4f}'.format(mean_squared_error(y, yFit)))  # MSE 均方误差
    print('平均绝对值误差：{:.4f}'.format(mean_absolute_error(y, yFit)))  # MAE 平均绝对误差
    print('中位绝对值误差：{:.4f}'.format(median_absolute_error(y, yFit)))  # 中值绝对误差
    # 计算 F统计量 和 F检验的 P值
    m = X.shape[1]
    n = X.shape[0]
    yMean = np.mean(y)
    SST = sum((y-yMean)**2)  # SST: 总平方和
    SSR = sum((yFit-yMean)**2)  # SSR: 回归平方和
    SSE = sum((y-yFit)**2)  # SSE: 残差平方和
    Fstats = (SSR/m) / (SSE/(n-m-1))  # F 统计量
    probFstats = stats.f.sf(Fstats, m, n-m-1)  # F检验的 P值
    print('F统计量：{:.4f}'.format(Fstats))
    print('FF检验的P值：{:.4e}'.format(probFstats))
    
    # 绘图：原始数据点，拟合曲线
    fig, ax = plt.subplots(figsize=(8, 6))  # YouCans, XUPT
    ax.plot(range(len(y)), y, 'b-.', label='Sample')  # 样本数据
    ax.plot(range(len(y)), yFit, 'r-', label='Fitting')  # 拟合数据
    ax.legend(loc='best')  # 显示图例
    plt.title('Regression analysis with sales of toothpaste by SKlearn')
    plt.xlabel('period')
    plt.ylabel('sales')
    plt.show()

    return
# = 关注 Youcans，分享原创系列 https://blog.csdn.net/youcans =
if __name__ == '__main__':
    main()

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90

程序运行结果：

Model1: Y = b0 + b1*x1 + b2*x2
回归截距: w0=4.4074933246887875
回归系数: w1=[1.58828573 0.56348229]
R2 确定系数：0.8860
均方误差：0.0511
平均绝对值误差：0.1676
中位绝对值误差：0.1187

Model3: Y = b0 + b1*x1 + b2*x2 + b3*x2**2
回归截距: w0=17.324368548878198
回归系数: w1=[ 1.30698873 -3.69558671  0.34861167]
R2 确定系数：0.9054
均方误差：0.0424
平均绝对值误差：0.1733
中位绝对值误差：0.1570
F统计量：82.9409
F检验的P值：1.9438e-13

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17

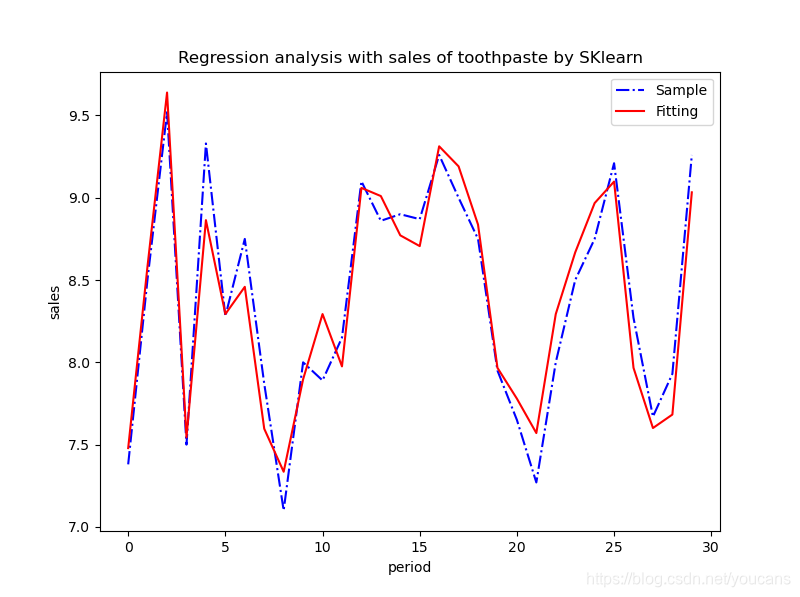
在这里插入图片描述

程序说明：

  1. 用 LinearRegression() 类处理多元线性回归问题，模型对训练样本数据的格式要求为：输入数据 X 是 array 类型的 n*m 二维数组，输出数据 y 是 array类型的 n*1 数组（也可以用 n*k 表示多变量输出）。例程中给出了两种数据转换的方式：Model 1 从 Pandas 的 dataframe 数据转换得到模型要求的 array 类型二维数组，这在 Pandas 读取数据文件时非常方便；Model3 则用 Numpy 的 np.column_stack 数组拼接获得 array 类型二维数组。
  2. 本例程的问题和数据《Python学习笔记-StatsModels 统计回归（3）模型数据的准备》中相同，来自：姜启源、谢金星《数学模型（第 3版）》，高等教育出版社。
  3. 为了便于与 StatsModels 统计回归结果进行比较，例程所采用的模型也与该文一致：Model1 中使用特征变量 ‘difference’, ‘advertise’ 建立线性回归模型，Model3 中使用特征变量 ‘difference’, ‘advertise’ 及 ‘advertise’ 的二次项（ x2**2）建立线性回归模型。SKlearn 与 StatsModels 对这两个模型的参数估计结果、预测结果和 R2确定系数都完全相同，表明用 SKlearn 与 StatsModels 工具包都可以实现线性回归。
  4. StatsModels 工具包提供的模型检验的指标非常全面、详细，对模型检验和统计分析非常重要。而 SKlearn 包所提供的统计检验指标很少，F检验、T 检验、相关系数的显著性检验指标都没有，根本原因在于 SKlearn 是机器学习库而非统计工具箱，关注点是模型精度和预测性能，而不在于模型的显著性。
  5. 为了解决缺少模型显著性检验指标的问题，例程中增加了一段 计算 F统计量 和 F检验P值 的程序可供参考。

版权说明：
　　本文内容及例程为作者原创，并非转载书籍或网络内容。
YouCans 原创作品
Copyright 2021 YouCans, XUPT
Crated：2021-05-12

欢迎关注 Youcans 原创系列，每周更新数模笔记

Python数模笔记-PuLP库（1）线性规划入门
Python数模笔记-PuLP库（2）线性规划进阶
Python数模笔记-PuLP库（3）线性规划实例
Python数模笔记-StatsModels 统计回归（1）简介
Python数模笔记-StatsModels 统计回归（2）线性回归
Python数模笔记-StatsModels 统计回归（3）模型数据的准备
Python数模笔记-StatsModels 统计回归（4）可视化
Python数模笔记-Sklearn （1）介绍
Python数模笔记-Sklearn （2）聚类分析
Python数模笔记-Sklearn （3）主成分分析
Python数模笔记-Sklearn （4）线性回归
Python数模笔记-Sklearn （5）支持向量机
Python数模笔记-模拟退火算法（1）多变量函数优化
Python数模笔记-模拟退火算法（2）约束条件的处理
Python数模笔记-模拟退火算法（3）整数规划问题
Python数模笔记-模拟退火算法（4）旅行商问题

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/正经夜光杯/article/detail/829965
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号