Leetcode - 周赛399

目录

一，3162. 优质数对的总数 I

二，3163. 压缩字符串 III

三，3164. 优质数对的总数 II

四， 3165. 不包含相邻元素的子序列的最大和

---

一，3162. 优质数对的总数 I

假设 x 是 nums1 数组中的值，y 是 nums2 数组中值，我们要求的就是有几个 (x，y) 满足

x % (y * k) == 0，可以直接暴力 

代码如下：

class Solution {
    public int numberOfPairs(int[] nums1, int[] nums2, int k) {
        int ans = 0;
        for(int x : nums1){
            for(int y : nums2){
                if(x%(y*k)==0) ans++;
            }
        }
        return ans;
    }
}

二，3163. 压缩字符串 III

本题是一道模拟题，遍历word字符串，将相邻且字符相同的子字符串，写成数字+字符的形式，比如 "aaabbc"，写成 "3a2b1c"，注意，数字最大是9，也就是说如果遇到比如12个连续的'a'，我们要写成 "9a3a"。

代码如下： 

class Solution {
    public String compressedString(String word) {
        int cnt = 1;
        char[] ch = word.toCharArray();
        StringBuilder res = new StringBuilder();
        for(int i=1; i<ch.length; i++){
            if(ch[i] == ch[i-1] && cnt < 9){
                cnt++;
            }else{
                res.append(cnt);
                res.append(ch[i-1]);
                cnt = 1;
            }
        }
        if(cnt > 0){
            res.append(cnt);
            res.append(ch[ch.length-1]);
        } 
        return res.toString();
    }
}

三，3164. 优质数对的总数 II

1. 预处理被除数：

• 要求满足 x % (y * k) == 0 的数对（x，y），可以先枚举nums1数组，使用哈希表统计出 x / k 的所有因子及其对应的数量，再枚举 nums2 数组，看 y 是否是x/k的因子（即是否在哈希表中），如果存在，加上对应的值。最终得出答案

2.预处理除数

• 除了上述做法，我们还可以先枚举nums1数组，使用哈希表统计出 x / k 及其对应的数量，枚举nums2数组，枚举 y 的倍数及其数量，看是否在哈希表中，如果存在，加上对应的值。最终得出答案

代码如下：

class Solution {
    //预处理被除数x
    public long numberOfPairs(int[] nums1, int[] nums2, int k) {
        Map<Integer, Integer> map = new HashMap<>();
        for(int x : nums1){//统计 <x/k 的因子, 对应的数量>
            if(x%k == 0){
                for(int i=1; i<=Math.sqrt(x/k); i++){
                    if(x/k%i == 0){
                        map.merge(i, 1, Integer::sum);
                        if(i < x/k/i)
                            map.merge(x/k/i, 1, Integer::sum);
                    }
                }
            }
        }
        long ans = 0;
        for(int y : nums2){
            ans += map.getOrDefault(y, 0);
        }
        return ans;
    }
}
 
 
class Solution {
    //预处理除数y
    public long numberOfPairs(int[] nums1, int[] nums2, int k) {
        //O(n+m+(mx/k)logm)
        Map<Integer, Integer> map1 = new HashMap<>();
        long mx = 0;
        for(int x : nums1){//统计 <x/k,x/k的数量>
            if(x%k == 0){
                map1.merge(x/k, 1, Integer::sum);
                mx = Math.max(mx, x/k);
            }
        }
        Map<Integer, Integer> map2 = new HashMap<>();
        for(int y : nums2){
            map2.merge(y, 1, Integer::sum);
        }
        long ans = 0;
        for(int y : map2.keySet()){ 
            int s = 0;
            for(int j=y; j<=mx; j+=y){//枚举 y 的倍数
                s += map1.getOrDefault(j, 0);
            }
            ans += (long) s * map2.get(y);
        }
        return ans;
    }
}

四， 3165. 不包含相邻元素的子序列的最大和

本题一看就是一道标准的打家劫舍问题，直接上代码：

class Solution {
    public int maximumSumSubsequence(int[] nums, int[][] queries) {
        int MOD = (int)1e9 + 7;
        int n = nums.length;
        int[] f = new int[n];
        int ans = 0;
        for(int[] q : queries){
            nums[q[0]] = q[1];
            f[0] = Math.max(0, nums[0]);
            for(int i=1; i<n; i++){
                f[i] = Math.max(f[i-1], (i>1?f[i-2]:0)+nums[i]);
            }
            System.out.println(f[n-1]);
            ans = (ans+f[n-1])%MOD;
        }
        return ans;
    }
}

但是上述做法会超时，需要换一种做法，这题实际上需要使用线段树动态维护[0，n-1]的最大值，就是将 [l，r] = [l，mid] + [mid+1，r]，不断的分治，但是由于题目要求不包含相邻元素，也就是说mid 和 mid+1这两个点最多只能取一个，而只靠一维数组无法维护，所以需要一个二维数组f[n][4]，这里先用f00，f01，f10，f11表示一下它们的状态：

• f00:表示[l,r]l,r都不选的合法最大值
• f01:表示[l,r]l不选的合法最大值(r可选可不选)
• f10:表示[l,r]r不选的合法最大值(l可选可不选)
• f11:表示[l,r]都可以选的合法最大值(l,r可选可不选)

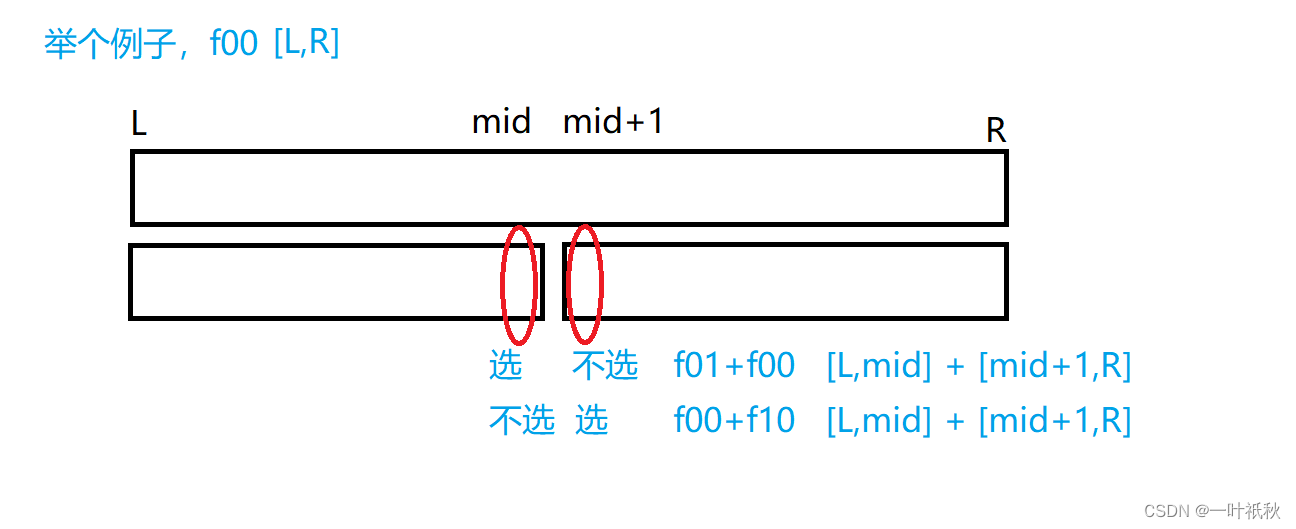
它们之间的递推关系：

• f00 = max(f01+f00, f00+f10)
• f01 = max(f00+f11, f01+f01)
• f10 = max(f10+f10, f11+f00)
• f11 = max(f10+f11, f11+f01)

画个图来理解一下：

剩下的基本都是线段树基本方法，没什么变化，代码如下：

class Solution {
    //f00:表示[l,r]l,r都不选的合法最大值
    //f01:表示[l,r]l不选的合法最大值(r可选可不选)
    //f10:表示[l,r]r不选的合法最大值(l可选可不选)
    //f11:表示[l,r]都可以选的合法最大值(l,r可选可不选)
    //[l, r] = [l, mid] + [mid+1, r]
    // 00 01 10 11
    //f00 = max(f01+f00, f00+f10)
    //f01 = max(f00+f11, f01+f01)
    //f10 = max(f10+f10, f11+f00)
    //f11 = max(f10+f11, f11+f01)
    int[][] f;
    int[] a;
    void maintain(int i){
        f[i][0] = Math.max(f[i<<1][1]+f[i<<1|1][0], f[i<<1][0]+f[i<<1|1][2]);
        f[i][1] = Math.max(f[i<<1][0]+f[i<<1|1][3], f[i<<1][1]+f[i<<1|1][1]);
        f[i][2] = Math.max(f[i<<1][2]+f[i<<1|1][2], f[i<<1][3]+f[i<<1|1][0]);
        f[i][3] = Math.max(f[i<<1][2]+f[i<<1|1][3], f[i<<1][3]+f[i<<1|1][1]);
    }
    void build(int l, int r, int i){
        if(l == r){
            f[i][3] = Math.max(0, a[l]);
        }else{
            int mid = (l + r) / 2;
            build(l, mid, i<<1);
            build(mid+1, r, i<<1|1);
            maintain(i);
        }
    }
    void update(int l, int r, int i, int R, int val){
        if(l == r){
            f[i][3] = Math.max(0, val);
            return;
        } 
        int mid = (l + r) / 2;
        if(R <= mid){
            update(l, mid, i<<1, R, val);
        }else{
            update(mid+1, r, i<<1|1, R, val);
        }
        maintain(i);
    }
    int query(int l, int r, int i){
        return f[i][3];
    }
    public int maximumSumSubsequence(int[] nums, int[][] queries) {
        int MOD = (int)1e9 + 7;
        int n = nums.length;
        f = new int[n<<2][4];
        a = nums;
        build(0, n-1, 1);
        int ans = 0;
        for(int[] q : queries){
            update(0, n-1, 1, q[0], q[1]);
            ans = (ans + query(0, n-1, 1))%MOD;
        }
        return ans%MOD;
    }
}