- 1嵌入式系统中串口通信粘包问题的解决方案(C语言)
- 2Android:禁用全局多点触控_android xml 多指点击禁用
- 3开源免费的物联网网关 IoT Gateway_iotgateway
- 4Flink系列六:Flink SQl 之常用的连接器(Connector)_flink connector
- 5Python 类内置函数__next__()用法记录_python df.next
- 6基于微信小程序的高校新生报道管理系统的设计与实现_基于微信小程序的新生报到管理系统的er图
- 7自然语言处理前馈网络(多层感知机与卷积神经网络)
- 8IntelliJ IDEA全局设置秘籍:JDK、Maven、编码格式全攻略_intellij idea 设置jdk版本
- 9Web实时通信的学习之旅:轮询、WebSocket、SSE的区别以及优缺点_sse 轮询 websocket
- 10Spark调试_spark 调试
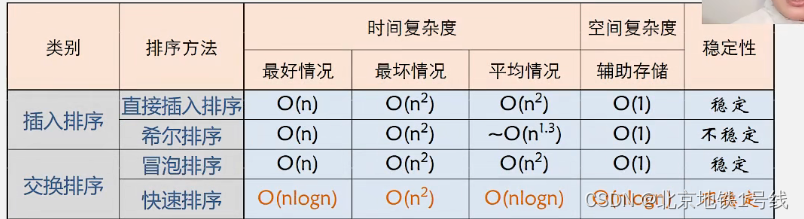
24.排序,插入排序,交换排序_.对顺序表进行排序,分别使用直接插入排序、折半插入排序、快速排序、简单选择排序
赞
踩
目录
排序:将一组杂乱无章的数据按一定规律顺次排列起来。即,将无序序列排成一个有序序列(由小到大或由大到小)的运算。如果参加排序的数据结点包含多个数据域,那么排序往往是针对其中某个域而言。
排序方法:
- 按数据存储介质:内部排序和外部排序
- 按比较器个数:串行排序和并行排序
- 按主要操作:比较排序和基数排序(后面会讲)
- 按辅助空间:原地排序和非原地排序
- 按稳定性:稳定排序和非稳定排序
- 按自然性:自然排序和非自然排序
本章学习内容:
- 插入排序:直接插入排序、折半插入排序、希尔排序
- 交换排序:冒泡排序、快速排序
- 选择排序:简单选择排序、堆排序
- 归并排序:2-路归并排序
- 基数排序
衡量排序算法的指标有时间复杂度,空间复杂度和稳定性等。对于稳定性做一点说明。稳定排序指的是能够使任何数值相等的元素,排序以后相对次序不变。例如,下面的示例1是稳定排序,示例2就不是稳定排序。
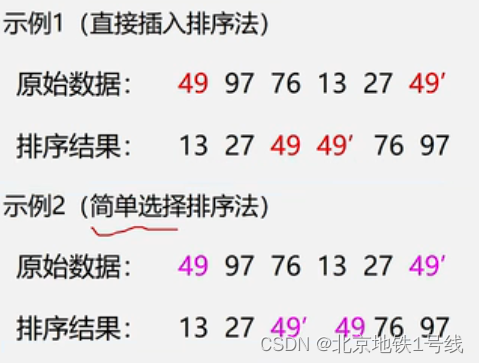
排序的稳定牲只对结构类型数据排序有意义。例如:n个学生信息(学号、姓名、语文、数学、英语、总分),首先按数学成绩从高到低排序,然后按照总分从高到低排序。若是稳定排序,总分相同的情况下,数学成绩高的仍然排在前面。
存储结构:本章基于的存储结构均以顺序表存储。
- #define MAXSIZE 20 //设记录不超过20个
- typedef int KeyType; //设关键字为整型量(int型)
-
- typedef struct{ //定义每个记录(数据元素)的结构
- KeyType key; //关键字
- InfoType otherinfo; //其它数据项
- }RedType; //Record Type
-
- typedef struct{ //定义顺序表的结构
- RedType r[MAXSIZE+1]; //存储顺序表的向量
- //r[0]一般作哨兵或缓冲区
- int length; //顺序表的长度
- }SqList;
一. 插入排序
基本思想:每步将一个待排序的对象,按其关键码大小,插入到前面已经排好序的一组对象的适当位置上,直到对象全部插入为止。即边插入边排序。
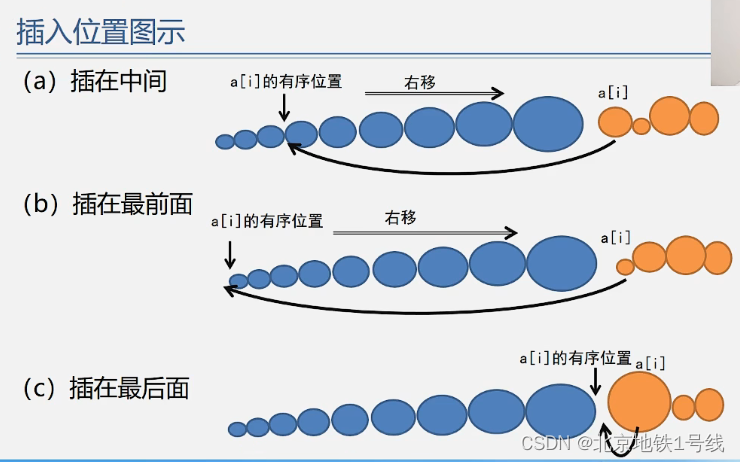
根据确定插入位置的方法不同,我们可以有以下三种插入排序的方法:
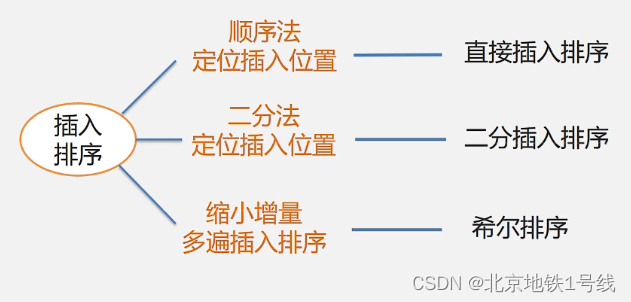
(1)直接插入排序
顺序法定位插入位置:一个一个比较。
- 首先,复制待插入的元素,复制插入元素。x=a[i];
- 然后,记录后移,查找插入位置;for(j=i-1; j>=0&&x<a[j];j--),a[j+1]=a[j];
- 最后,插入到正确位置,a[j+1]=x;
对于复制待插入的元素,我们可以使用哨兵。把待插入的元素复制到0号位,这样省去了越界的判断:
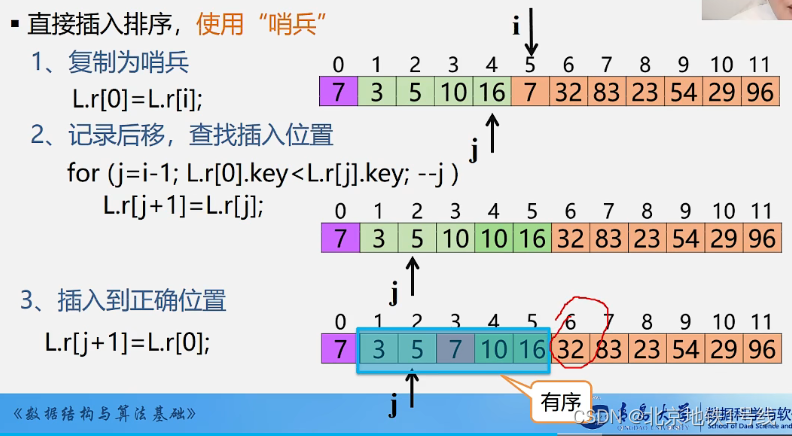
此外,如果待插入元素比有序表最后一位还大,那就不用进行任何操作了,这个位置就是待插入元素的位置。
- void InsertSort(SqList &L){
- int i, j;
- for(i=2; i<=L.length; ++i){ //第1个元素不用排序,从插入第2个元素开始
- if (L.r[i].key < L.r[i-1].key){ //若"<",需将L.r[i]插入有序子表
- L.r[0]=L.r[i]; //复制为哨兵
- for(j=i-1; L.r[0].key<L.r[j].key; --j){
- L.r[j+1]=L.r[j]; //记录后移
- }
- L.r[j+1]=L.r[0]; //插入到正确位置
- }
- }
- }
下面我们来分析时间效率。实现排序的基本操作有两个:(1)“比较”序列中两个关键字的大小;(2)“移动”记录。最好的情况是,关键字在记录序列中顺序有序。这时比较的次数是,不需要移动。最坏的情况是,关键字在记录序列中逆序有序。这时比较的次数是
,移动的次数是
,从而我们可以得到以下结论:
- 原始数据越接近有序,排序速度越快;
- 最坏情况下(输入数据是逆有序的)Tw(n)=O(n^2);
- 平均情况下,耗时差不多是最坏情况的一半Te(n)=O(n^2);
- 空间复杂度是O(1);
- 要提高查找速度,可以从减少元素的比较次数和减少元素的移动次数入手;
(2)折半插入排序
查找插入位置采用折半查找法。
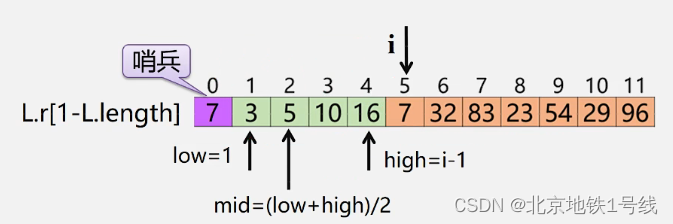
- void BlnsertSort (SqList &L){
- for (i = 2; i<= L.length ; ++i){ //依次插入第2~第n个元素
- L.r[0] = L.r[i]; //当前插入元素存到“哨兵”位置
- low = 1 ; high = i-1; //采用二分查找法查找插入位置
- while (low <= high){
- mid = (low + high)/2;
- if (L.r[0].key < L.r[mid].key) high = mid-1;
- else low = mid + 1;
- } //循环结束,high+1则为插入位置
- for (j=i-1; j>=high+1; --j)
- L.r[j+1] = L.r[j]; //移动元素
- L.r[high+1] = L.r[0]; //插入到正确位置
- }// BInsertSort
最后我们分析算法的时间效率。折半查找比顺序查找快,所以折半插入排序就平均性能来说比直按插入排序要快。它所需要的关键码比较次数与待排序对象序列的初始排列无关,仅依赖于对象个数。在插入第i个对象时,需要经过次关键码比较,才能确定它应插入的位置。
当n较大时,总关键码比较次数比直接插入排序的最坏情况要好得多,但比其最好情况要差。在对象的初始排列已经按关键码排好序或接近有序时,直接插入排序比折半插入排序执行的关键码比较次数要少。对移动次数,折半插入排序的对象移动次数与直接插入排序相同,依赖于对象的初始排列。所以折半插入排序减少了比较次数,但没有减少移动次数。平均性能优于直接插入排序。其时间复杂度为O(n^2),空间复杂度是O(1),是一种稳定的排序方法。
(3)希尔排序
直接排序什么时候效率较高?一是序列基本有序,二是序列长度较小。基于此我们提出希尔排序的基本思路:先将整个待排记录序列分割成若干子序列,分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行一次直接插入排序。希尔排序的算法特点是:
- 一次移动,移动位置较大,跳跃式地接近排序后的最终位置
- 最后一次只需要少量移动
- 增量序列必须是递减的,最后一个必须是1
- 增量序列应该是互质的
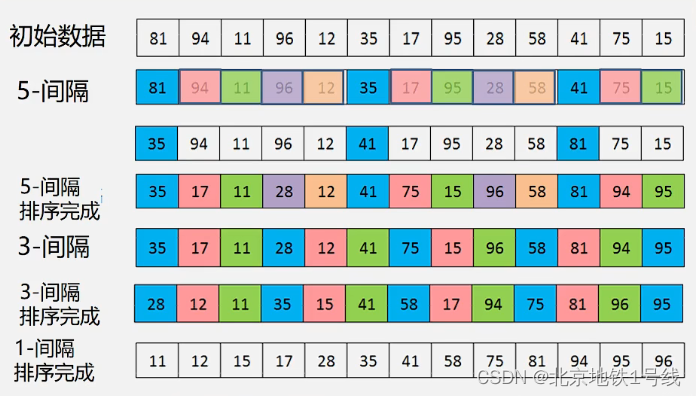
首先:定义增量序列,刚才的例子中
然后:对每个进行“
-间隔”插入排序(k=M,M-1,...1)。
- //主程序
- void ShellSort(Sqlist &L,int dlta[],int t){
- //按增量序列dlta[0..t-1]对顺序表L作希尔排序,t是增量序列的长度
- for(k=O; k<t; ++k)
- Shellnsert(L,dlta[k]); //一趟增量为dlta[k]的插入排序
- }//ShellSort
-
- void ShellInsert(SqList &L,int dk){
- //对顺序表L进行一趟增量为dk的Shell排序,dk为步长因子
- //和一趟直接插入排序相比,做了以下修改:
- //1.前后记录位置的增量是dk,不是1
- //2.r[0]只是暂存单元,不是哨兵,当j<=0时,插入位置已找到
- for(i = dk+1; i <= L.length; ++i)
- //dk间隔排序,从dk+1开始排序,例如前面讲的一趟直接插入排序从第2个元素开始排序
- if(r[i].key < r[i-dk].key){ //比前面的大则不需要执行插入操作
- L.r[0] = L.r[i]; //暂存在L.r[0]
- for(j = i-dk; j>0 &&(r[0].key < r[j].key); j = j-dk)
- r[j+dk]=r[j]; //后移
- L.r[j+dk]=L.r[0]; //插入,退出循环时r[j]<r[0],所以插到L.r[j+dk]的位置
- }
- }

希尔排序的算法效率与增量序列的取值有关。
对于Hibbard增量序列,,相邻元素互质。最坏情况
;猜想:
;
Sedgewick增量序列{1,5,19,41,109...},或
。猜想:
,
;
希尔排序法是一种不稳定的排序算法,例如对下面d=2的情况:

总结:对希尔排序来说,时间复杂度是n和d的函数,空间复杂度是O(1),是一种不稳定的排序方法。关于如何选择最佳d序列,目前尚未有解决方案。但是,最后一个增量值必须为1,其他序列元素之间无除了1之外的公因子。此外,希尔排序不宜在链式存储结构上实现。
二. 交换排序
基本思想:两两比较,如果发生逆序则交换,直到所有记录都排好序为止。
常见的交换排序方法:冒泡排序,快速排序。
(1)冒泡排序
给定初始序列:21,25,49,25*,16,08,n=6。
第1趟:
位置0,1进行比较——判断——不交换——结果:21,25,49,25*,16,08
位置1,2进行比较——判断——不交换——结果:21,25,49,25*,16,08
位置2,3进行比较——判断——交换——结果:21,25,25*,49,16,08
位置3,4进行比较——判断——交换——结果:21,25,25*,16,49,08
位置4,5进行比较——判断——交换——结果:21,25,25*,16,08,49
第1趟结束后:21,25,25*,16,08,49
第2趟:
位置0,1进行比较——判断——不交换——结果:21,25,25*,16,08,49
位置1,2进行比较——判断——不交换——结果:21,25,25*,16,08,49
位置2,3进行比较——判断——交换——结果:21,25,16,25*,08,49
位置3,4进行比较——判断——交换——结果:21,25,16,08,25*,49
第2趟结束后:21,25,16,08,25*,49
继续下一趟,每一趟增加一个有序元素。
第3趟结果:21,16,08,25,25*,49
第4趟结果:16,08,21,25,25*,49
第5趟结果:08,16,21,25,25*,49
总结:n个记录,需要比较n-1趟。第m趟需要比较n-m次。
- void bubble_sort(SqList &L){ //冒泡排序算法
- int m,i,j;
- RedType x; //交换时临时存储
- for(m=1; m<=n-1; m++){ //总共需n-1趟
- for(j=1; j<=n-m; j++) //第m趟需要比较n-m次
- if(L.r[j].key > L.r[j+1].key){ //发生逆序
- x=L.r[j]; L.r[j]=L.r[j+1]; L.r[j+1]=x; //交换
- }//endif
- }//for
- }
冒泡排序的优点:每趟结束时,不仅能挤出一个最大值到最后面位置,还能同的部力理顺其他元素。实际上,一旦某一趟比较时不出现记录交换,说明已排好序了,就可以结束本算法。所以我们可以增设一个标识flag:
- void bubble_sort(SqList &L){ //改进的冒泡排序算法
- int m,i,j;
- flag=1; //flag作为是否有交换的标记
- RedType x;
- for(m=1; m<=n-1 && flag==1; m++){
- flag=0;
- for(j=1; j<=n-m; j++){
- if(L.r[j].key>L.r[j+1].key){//发生逆序
- flag=1; //发生交换,flag置为1,若本趟没发生交换,flag保持为零
- x=L.r[j]; L.r[j]=L.r[j+1]; L.r[j+1]=x; //交换
- }//endif
- }//for
- }
- }
下面分析时间复杂度。最好情况是全为正序,这时比较次数是n-1,移动的次数是0;最坏情况是全为逆序,比较次数是,移动次数是
(包含向中间辅助变量x移动)。所以,冒泡排序最好时间复杂度是O(n),最坏时间复杂度为O(n^2),平均时间复杂度为O(n^2)。冒泡排序算法中增加一个辅助空间temp,辅助空间为S(n)=O(1),冒泡排序是稳定的排序算法。
(2)快速排序
快速排序是一种改进的交换排序。基本思想是递归思想:任取一个元素(如:第一个)为中心pivot,所有比它小的元素一律前放,比它大的元素一律后放,形成左右两个子表。对各子表重新选择中心元素并依此规则调整,直到每个子表的元素只剩一个(结束条件)。下面的过程,每个表中都选取第一个作为中心点(分界点)。
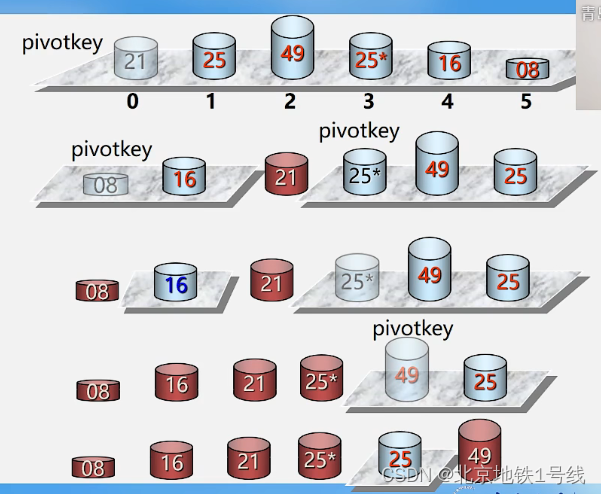
例如:给定序列

序列共8个数,界点直接取第一个数49,并把它搬到0号位。指针low=1,high=8.由于第1个位置已空,我们从后往前移动high,找一个小于界点的数把它搬到1号位。high--,当high=7的时候,数27满足,把27搬到1号位。此时7位空出来,我们向后移动low,找一个大于界点的数搬到空出来的7号位。low++,当low=3的时候,数65满足,把65搬到7号位,此时3号位空出来。我们再往前移动high,找一个大于界点的数搬到3号位。当high=6,数字13符合,13搬到3号位,6号位又空出。继续往后移动low,low=4,数97符合,97搬到6号位,4号位空出。然后往前移动high,high=5没有符合题意的,继续向前移动至high=4,此时high与low都重合。再把界点49填到4号位。此时8个数字的表就能以4号位49为界分成两个子表:前面1-3位,后面5-8位。然后在对两个子表分别执行相同的操作。
总结:①每一趟的子表的形成是采用从两头向中间交替式逼近法;②由于每趟中对各子表的操作都相似,可采用递归算法。
- void main(){
- QSort(L, 1, L.length);
- }
-
- void QSort(SqList &L, int low, int high){ //对顺序表L快速排序
- if(low < high){ //长度大于1
- pivotloc = Partition(L, low, high);
- //将L一分为二,pivotloc为中心点元素排好序的位置
- QSort(L, low, pivotloc-1); //对低子表递归排序
- QSort(L, pivotloc+1, high); //对高子表递归排序
- }//end if
- }//QSort
-
- int Partition(SqList &L, int low, int high){
- L.r[0] = L.r[low]; //取[low,high]的第一个元素作为中心点,并搬前面去
- pivotkey = L.r[low].key; //这里也是取中心点
- while (low < high){ //循环终止的条件是low=high
- while (low < high && L.r[high].key >= pivotkey) --high;
- //low指针指的地方空出,前移high,直到找到一个小于pivotkey的
- L.r[low] = L.r[high]; //然后搬到空出的地方low,此时high又空出来
-
- while (low < high && L.r[low].key <= pivotkey) ++low;
- //high指针指的地方空出,后移low,直到找到一个大于pivotkey的
- L.r[high] = L.r[low]; //然后搬到空出的地方high,此时low又空出来
- }
- L.r[low]=L.r[0]; //退出循环,再把最后指针重合的地方就是空的地方,填回中心点
- return low; //返回中心点所在的位置
- }

下面分析算法效率:可以证明,时间复杂度是,其中对上面的Qsort()是
,对下面的Partition()是
。实验结果表明:就平均计算时间而言,快速排序是我们所讨论的所有内排序方法中最好的一个。
接下来分析空间复杂度:快速排序不是原地排序。由于程序中使用了递归,需要递归调用栈的支持,而栈的长度取决于递归调用的深度(即使不用递归,也需要用用户栈)。在平均情况下,需要O(logn)的栈空间;最坏情况下,栈空间可达O(n)。
快速排序同前面的希尔排序,它也是不稳定的排序算法。例如:49,38,49*,20,97,76,经过一次划分后:20,38,49*,49,97,76。
快速排序不适于对原本有序或基本有序的记录序列进行排序。例如,对(46,50,68,74,79,85,90)进行快速排序,会发现:由于每次枢轴记录的关键字都是小于其它所有记录的关键字,致使一次划分之后得到的子序列(1)的长度为0,这时已经退化成为没有改进措施的冒泡排序。
划分元素的选取是影响时间性能的关键。输入数据次序越乱,所选划分元素值的随机性越好,排序速度反而越快,快速排序不是自然排序方法。需要注意的是,改变划分元素的选取方法,至多只能改变算法平均情况的下的世界性能,无法改变最坏情况下的时间性能。即最坏情况下,快速排序的时间复杂度总是O(n^2)。