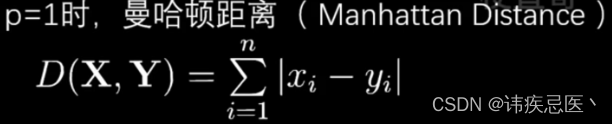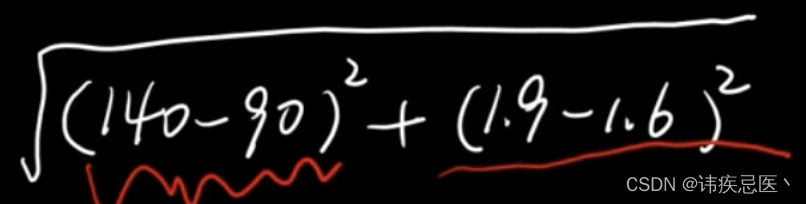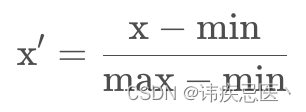- 1Cobalt Strike 的通信过程 & 协议_cobalt strike密钥
- 2[晓理紫]每日论文推送(有中文摘要或代码或项目地址)---大模型,扩散模型_customize it 3d
- 3RNN、LSTM相关知识总结。_rnn与lstm的联系与区别
- 4中间件的分类_操作系统数据库中间件归位哪一类
- 5scikit-learn(sklearn)学习笔记五_from sklearn import datasets from sklearn.datasets
- 6 Scrum vs Waterfall vs Agile vs Lean vs Kanban
- 7上采样、下采样、过采样、欠采样是什么?_欠采样和过采样 谢邀
- 8颜色的十六进制编码_荧光黄十六进制
- 9springboot集成elasticsearch,实现搜索提示补全功能_spring boot整合 es自动补全
- 10NLP知识包--语义分析&智能问答&工具_语义分析工具
机器学习KNN最邻近分类算法
赞
踩
1、KNN算法简介
KNN (K-Nearest Neighbor) 最邻近分类算法,其核心思想“近朱者赤,近墨者黑”,由你的邻居来推断你的类别。
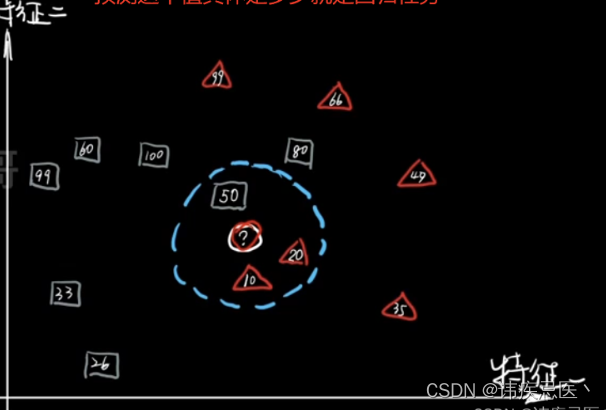
图中绿色圆归为哪一类?
1、如果k=3,绿色圆归为红色三角形
2、如果k=5,绿色圆归为蓝色正方形
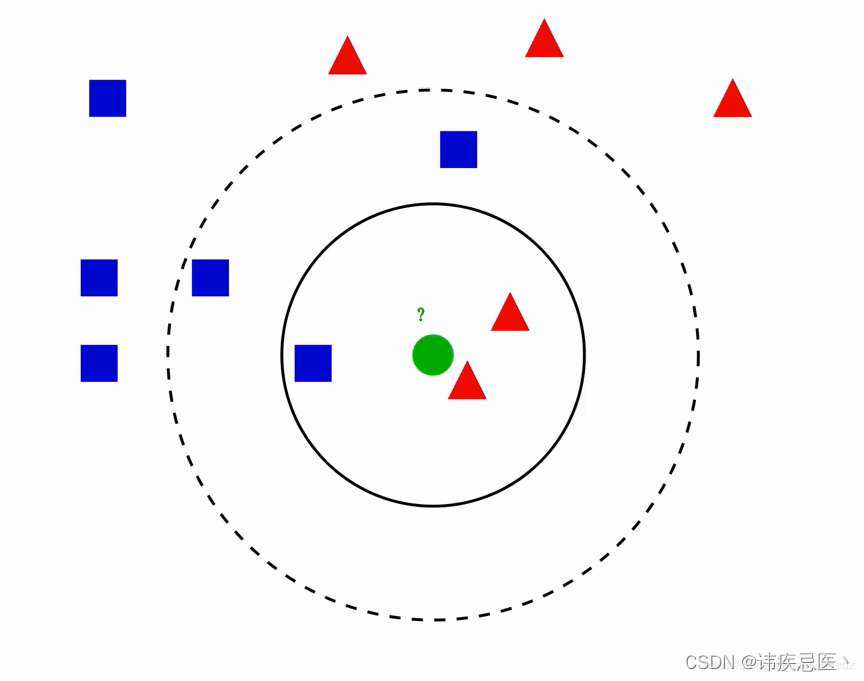
knn算法实现原理:为判断未知样本数据的类别,以所有已知样本数据作为参照物,计算未知样本数据与所有已知样本数据的距离,从中选取k个与已知样本距离最近的k个已知样本数据,根据少数服从多数投票法则,将未知样本与K个最邻近样本中所属类别占比较多的归为一类。(我们还可以给邻近样本加权,距离越近的权重越大,越远越小)
2、KNN算法实现
1、k值选择:太小容易产生过拟合问题,过度相信样本数据,太大容易产生欠拟合问题,与数据贴合不够解密,决策效率低。
2、样本数据归一化:最简单的方式就是所有特征的数值都采取归一化处置。
3、一个距离函数计算两个样本之间的距离:通常使用的距离函数有:欧氏距离、曼哈顿距离、汉明距离等,一般选欧氏距离作为距离度量,但是这是只适用于连续变量。在文本分类这种非连续变量情况下,汉明距离可以用来作为度量。通常情况下,如果运用一些特殊的算法来计算度量的话,K近邻分类精度可显著提高。
4、KNN优点:
1.简单,易于理解,易于实现,无需估计参数,无需训练
2. 适合对稀有事件进行分类
3.特别适合于多分类问题(multi-modal,对象具有多个类别标签), KNN比SVM的表现要好
5、KNN缺点:
KNN算法在分类时有个主要的不足是,当样本不平衡时,如一个类的样本容量很大,而其他类样本容量很小时,有可能导致当输入一个新样本时,该样本的K个邻居中大容量类的样本占多数,如下图所示。该算法只计算最近的邻居样本,某一类的样本数量很大,那么或者这类样本并不接近目标样本,或者这类样本很靠近目标样本。无论怎样,数量并不能影响运行结果。可以采用权值的方法(和该样本距离小的邻居权值大)来改进。该方法的另一个不足之处是计算量较大,因为对每一个待分类的文本都要计算它到全体已知样本的距离,才能求得它的K个最近邻点。
可理解性差,无法给出像决策树那样的规则。
实现KNN算法简单实例
1、样本数据散点图展示
# KNN算法实现
import numpy as np
import matplotlib.pyplot as plt
# 样本数据
data_X = [
[1.3,6],
[3.5,5],
[4.2,2],
[5,3.3],
[2,9],
[5,7.5],
[7.2,4],
[8.1,8],
[9,2.5],
]
# 样本标记数组
data_y = [0,0,0,0,1,1,1,1,1]
# 将数组转换成np数组
X_train = np.array(data_X)
y_train = np.array(data_y)
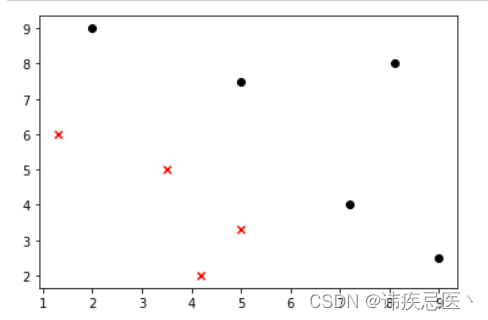
# 散点图绘制
# 取等于0的行中的第0列数据X_train[y_train==0,0]
plt.scatter(X_train[y_train==0,0],X_train[y_train==0,1],color='red',marker='x')
# 取等于1的行中的第1列数据X_train[y_train==1,0]
plt.scatter(X_train[y_train==1,0],X_train[y_train==1,1],color='black',marker='o')
plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
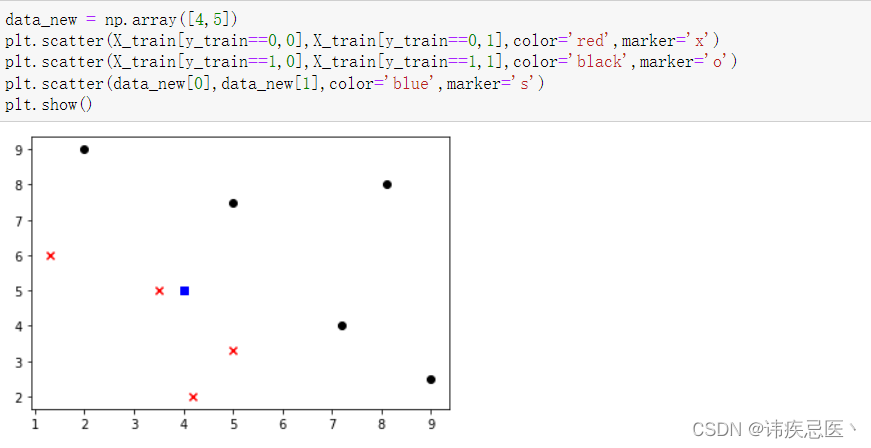
2、新的样本数据,判断它属于哪一类
data_new = np.array([4,5])
plt.scatter(X_train[y_train==0,0],X_train[y_train==0,1],color='red',marker='x')
plt.scatter(X_train[y_train==1,0],X_train[y_train==1,1],color='black',marker='o')
plt.scatter(data_new[0],data_new[1],color='blue',marker='s')
plt.show()
- 1
- 2
- 3
- 4
- 5
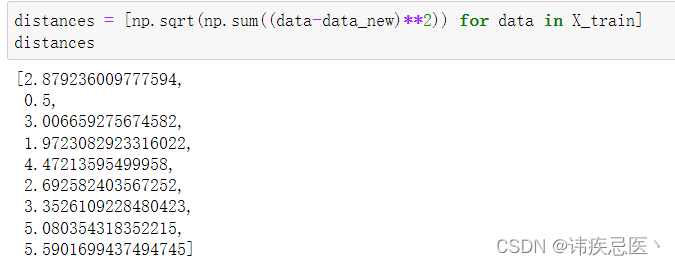
3、计算新样本点与所有已知样本点的距离
# 样本数据-新样本数据 的平方,然后开平,存储距离值到distances中
distances = [np.sqrt(np.sum((data-data_new)**2)) for data in X_train]
# 按照距离进行排序,返回原数组中索引 升序
sort_index = np.argsort(distances)
# 随机选一个k值
k = 5
# 距离最近的5个点进行投票表决
first_k = [y_train[i] for i in sort_index[:k]]
# 使用计数库统计
from collections import Counter
# 取出结果为类别0
predict_y = Counter(first_k).most_common(1)[0][0]
predict_y
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
2.1、调用scikit-learn库中KNN算法
2007年,Scikit-learn首次被Google Summer of Code项目开发使用,现在已经被认为是最受欢迎的机器学习Python库。
安装:pip install scikit-learn

# 使用scikit-learn中的KNN算法
from sklearn.neighbors import KNeighborsClassifier
# 初始化设置k大小
knn_classifier = KNeighborsClassifier(n_neighbors=5)
# 喂入数据集,以及数据类型
knn_classifier.fit(X_train,y_train)
# 放入新样本数据进行预测,需要先转换成二维数组
knn_classifier.predict(data_new.reshape(1,-1))
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
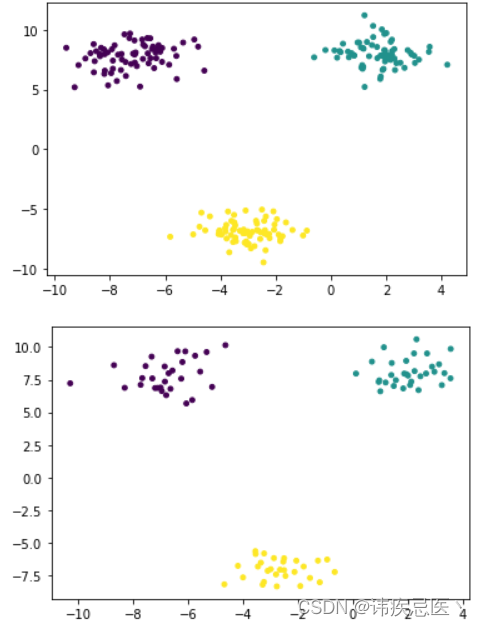
3、使用scikit-learn库生成数据集
生成的数据,画出的散点图
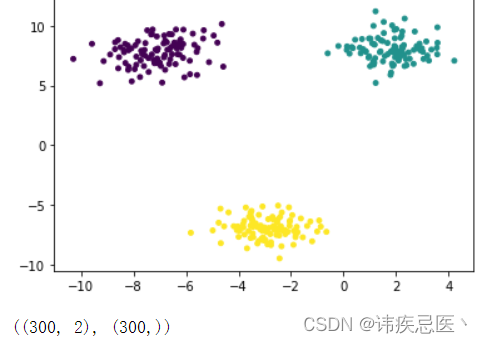
# 数据集生产
import numpy as np
from matplotlib import pyplot as plt
from sklearn.datasets import make_blobs
x,y = make_blobs(
n_samples=300, # 样本总数
n_features=2, # 生产二维数据
centers=3, # 种类数据
cluster_std=1, # 类内的标注差
center_box=(-10,10), # 取值范围
random_state=233, # 随机数种子
return_centers=False, # 类别中心坐标反回值
)
# c指定每个点颜色,s指定点大小
plt.scatter(x[:,0],x[:,1],c=y,s=15)
plt.show()
x.shape,y.shape
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
3.1、自定义函数划分数据集
将生成好的数据集,划分成训练数据集和测试数据集
# 数据集划分
np.random.seed(233)
# 随机生成数组排列下标
shuffle = np.random.permutation(len(x))
train_size = 0.7
train_index = shuffle[:int(len(x)*train_size)]
test_index = shuffle[int(len(x)*train_size):]
train_index.shape,test_index.shape
# 通过下标数组到数据集中取出数据
x_train = x[train_index]
y_train = y[train_index]
x_test = x[test_index]
y_test = y[test_index]
# 训练数据集
plt.scatter(x_train[:,0],x_train[:,1],c=y_train,s=15)
plt.show()
# 测试数据集
plt.scatter(x_test[:,0],x_test[:,1],c=y_test,s=15)
plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
3.2、使用scikit-learn库划分数据集
# sklearn划分数据集
from sklearn.model_selection import train_test_split
# 保证3个样本数保持原来分布,添加参数stratify=y
x_train,x_test,y_train,y_test = train_test_split(x,y,train_size=0.7,random_state=233,stratify=y)
from collections import Counter
Counter(y_test)
- 1
- 2
- 3
- 4
- 5
- 6
4、使用scikit-learn库对鸢尾花数据集进行分类
# 使用鸢尾花数据集
import numpy as np
from sklearn import datasets
# 加载数据集
iris = datasets.load_iris()
# 获取样本数组,样本类型数组
X = iris.data
y = iris.target
# 拆分数据集
# 不能直接拆分因为现在的y已经是排序好的,需要先乱序数组
# shuffle_index = np.random.permutation(len(X))
# train_ratio = 0.8
# train_size = int(len(y)*train_ratio)
# train_index = shuffle_index[:train_size]
# test_index = shuffle_index[train_size:]
# X_train = X[train_index]
# Y_train = y[train_index]
# X_test = X[test_index]
# Y_test = y[test_index]
from sklearn.model_selection import train_test_split
# 保证3个样本数保持原来分布,添加参数stratify=y
x_train,x_test,y_train,y_test = train_test_split(X,y,train_size=0.8,random_state=666)
# 预测
from sklearn.neighbors import KNeighborsClassifier
# 初始化设置k大小
knn_classifier = KNeighborsClassifier(n_neighbors=5
)
# 喂入数据集,以及数据类型
knn_classifier.fit(x_train,y_train)
# 如果关心预测结果可以跳过下面所有score返回得分
knn_classifier.score(x_test,y_test)
y_predict = knn_classifier.predict(x_test)
# 评价预测结果 将y_predict和真是的predict进行比较就可以了
accuracy = np.sum(y_predict == y_test)/len(y_test)
# accuracy
# sklearn中计算准确度的方法
from sklearn.metrics import accuracy_score
accuracy_score(y_test,y_predict)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
5、什么是超参数
在看机器学习时,经常碰到一个叫超参数的参数(hyper-parameter)的概念,通常情况下,需要对超参数进行优化,给学习选择一组最优超参数,以提高学习的性能和效果。
KNN算法中超参数表示什么,表示K的最近邻居有几个,是分类表决还是加权表决。
5.1、实现寻找超参数
1、加载鸢尾花数据集,并拆分数据集
# 超参数
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
import numpy as np
data = load_iris()
X = data.data
y = data.target
X.shape,y.shape
X_train,X_test,y_train,y_test = train_test_split(X,y,train_size=0.7,random_state=233,stratify=y)
X_train.shape,X_test.shape,y_train.shape,y_test.shape
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
2、寻找最优的一组超参数
# 遍历所有超参数,选取准确率
# uniform权重一直,越近权重越高distance
# p等于1折线曼哈顿距离计算方式,p=2欧式距离
best_score = -1
best_n = -1
best_p = -1
best_weight = ''
for i in range(1,20):
for weight in ['uniform','distance']:
for p in range(1,7):
neigh = KNeighborsClassifier(
n_neighbors=i,
weights=weight,
p = p
)
neigh.fit(X_train,y_train)
score = neigh.score(X_test,y_test)
if score>best_score:
best_score = score
best_n = i
best_p = p
best_weight = weight
print(best_n,best_p,best_weight,best_score)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
5.2、使用scikit-learn库实现
# 使用skleran超参数搜索
from sklearn.model_selection import GridSearchCV
params = {
'n_neighbors':[n for n in range(1,20)],
'weights':['uniform','distance'],
'p':[p for p in range(1,7)]
}
grid = GridSearchCV(
estimator=KNeighborsClassifier(),# 分类模型器
param_grid=params,# 参数
n_jobs=-1 # 自动设置并行任务数量
)
# 传入数据集
grid.fit(X_train,y_train)
# 得到超参数和得分
grid.best_params_
print(grid.best_score_)
# knn对象对测试数据集进行预测
y_predict = grid.best_estimator_.predict(X_test)
# sklearn中计算准确度的方法
from sklearn.metrics import accuracy_score
accuracy_score(y_test,y_predict)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
6、特征归一化
为什么做归一化?
比如说,现在有一组身高和体重的数据集(斤,米),求欧式距离的时候,可以发现身高在数据集中影响非常小,所以需要将数据归一化。
6.1、实现最大最小值归一化
最值归一化适用于,值分布在有限的范围里面,比如说考试分数0-100,它受特殊值影响比较大,比如正常体重在0-150斤,如果有一个1000斤,那么这个归一化的数据就会失真。
对上面数据做最大最小归一化操作
# 对数据做归一化
X[:5]
X[:,0] = (X[:,0] - np.min(X[:,0]))/(np.max(X[:,0])-np.min(X[:,0]))
X[:,1] = (X[:,1] - np.min(X[:,1]))/(np.max(X[:,1])-np.min(X[:,1]))
X[:,2] = (X[:,2] - np.min(X[:,2]))/(np.max(X[:,2])-np.min(X[:,2]))
X[:,3] = (X[:,3] - np.min(X[:,3]))/(np.max(X[:,3])-np.min(X[:,3]))
X[:5]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
6.2、实现零均值归一化
除了数据有明显的边界值,这种方式是最好的,原始数据-均值 / 标准差。
假设有一组数据集:[3, 6, 9, 12, 15]
计算平均值:
平均值 = (3 + 6 + 9 + 12 + 15) / 5 = 9
计算方差:
方差 = ((3-9)^2 + (6-9)^2 + (9-9)^2 + (12-9)^2 + (15-9)^2) / 5 = 18
计算标准差:
标准差 = √方差 = √18 ≈ 4.24
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
# 零均值归一化
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
import numpy as np
data = load_iris()
X = data.data
y = data.target
X[:5]
# 求均值
np.mean(X[:,0])
# 标准差
np.std(X[:,0])
X[:,0] = (X[:,0]- np.mean(X[:,0]))/(np.std(X[:,0]))
X[:,1] = (X[:,1]- np.mean(X[:,1]))/(np.std(X[:,1]))
X[:,2] = (X[:,2]- np.mean(X[:,2]))/(np.std(X[:,2]))
X[:,3] = (X[:,3]- np.mean(X[:,3]))/(np.std(X[:,3]))
X[:5]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
6.3、scikit-learn归一化使用

# scikit-learn中归一化
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
import numpy as np
data = load_iris()
X = data.data
y = data.target
X[:5]
from sklearn.preprocessing import StandardScaler
standard_scaler = StandardScaler()
standard_scaler.fit(X)
# 输出4列特征的均值
standard_scaler.mean_
# 输出标4列特标准差
standard_scaler.scale_
# X本身没有改变,我们需要将结果重新赋值给X
X = standard_scaler.transform(X)
X[:5]
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
7、KNN实现回归任务
预测这个值是多少,就是回归任务,思想和上面做分类一致,也是近朱者赤,近墨者黑,也是找距离最近k个点,也是民主投票,区别在于这里是求最近k个点的均值
7.1、实现KNN回归代码
# KNN 实现回归任务
# KNN算法实现
import numpy as np
import matplotlib.pyplot as plt
# 样本数据
data_X = [
[1.3,6],
[3.5,5],
[4.2,2],
[5,3.3],
[2,9],
[5,7.5],
[7.2,4],
[8.1,8],
[9,2.5],
]
# 样本标记数组
data_y = [0.1,0.3,0.5,0.7,0.9,1.1,1.3,1.5,1.7]
X_train = np.array(data_X)
y_train = np.array(data_y)
data_new = np.array([4,5])
plt.scatter(X_train[:,0],X_train[:,1],color='black')
plt.scatter(data_new[0],data_new[1],color='b',marker='s')
for i in range(len(y_train)):
plt.annotate(y_train[i],xy=X_train[i],xytext=(-15,-15),textcoords='offset points')
plt.show()
distance = [np.sqrt(np.sum((i-data_new)**2)) for i in X_train]
sort_index = np.argsort(distance)
k = 5
first_k = [y_train[i] for i in sort_index[:k]]
np.mean(first_k)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
7.2、使用scikit-learn库实现
# 使用scikit-learn实现
from sklearn.neighbors import KNeighborsRegressor
knn_reg = KNeighborsRegressor(n_neighbors=5)
knn_reg.fit(X_train,y_train)
predict_y = knn_reg.predict(data_new.reshape(1,-1))
predict_y
- 1
- 2
- 3
- 4
- 5
- 6
- 7
8、根据Boston数据集建立回归模型
import numpy as np
import matplotlib.pyplot as plt
import sklearn
from sklearn.model_selection import train_test_split
import pandas as pd
# 加载波士顿房屋数据集
data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
target = raw_df.values[1::2, 2]
# 数据准备
X = data
y = target
X.shape,y.shape
# 数据集划分
X_train,X_test,y_train,y_test = train_test_split(X,y,train_size=0.7,random_state=233)
# 建立回归模型
from sklearn.neighbors import KNeighborsRegressor
knn_reg = KNeighborsRegressor(n_neighbors=5,weights='distance',p=2)
knn_reg.fit(X_train,y_train)
# 计算得分,发现得分很低,原因是因为没有做归一化处理导致
knn_reg.score(X_test,y_test)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
做归一化处理之后输出得分
# 归一化操作
from sklearn.preprocessing import StandardScaler
standard_scaler = StandardScaler()
standard_scaler.fit(X_train)
# 对x train进行归一化操作
x_train = standard_scaler.transform(X_train)
x_test = standard_scaler.transform(X_test)
knn_reg.fit(x_train,y_train)
knn_reg.score(x_test,y_test)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11