FPGA——DDS_fpga dds

DDS
DDS 是直接数字式频率合成器（Direct Digital Synthesizer）的英文缩写，是一项关键的数字化技术。利用数字方式累加相位，再以相位之和作为地址来查询正弦函数表得到正弦波幅度的离散数字序列，最后经D/A变换得到模拟正弦波输出。在系统时钟一定的情况下，输出频率决定于频率寄存器中的频率字。而累加器的字长决定分辨率。与传统的频率合成器相比，DDS 具有低成本、低功耗、高分辨率和快速转换时间等优点，广泛使用在电信与电子仪器领域，是实现设备全数字化的一个关键技术。作为设计人员，我们习惯称它为信号发生器，一般用它产生正弦、锯齿、方波等不同波形或不同频率的信号波形，在电子设计和测试中得到广泛应用。
频率合成
频率合成，就是将一个具有低相噪,高精度和高稳定度等综合指标高的参考频率经过混频、倍频或分频等电路对其进行加、减、乘、除等运算，从而产生大量具有同样精度与稳定度的频率。
DDS 的基本结构
主要由相位累加器、相位调制器、波形数据表 ROM、D/A 转换器等四大结构组成，其中较多设计还会在数模转换器之后增加一个低通滤波器。

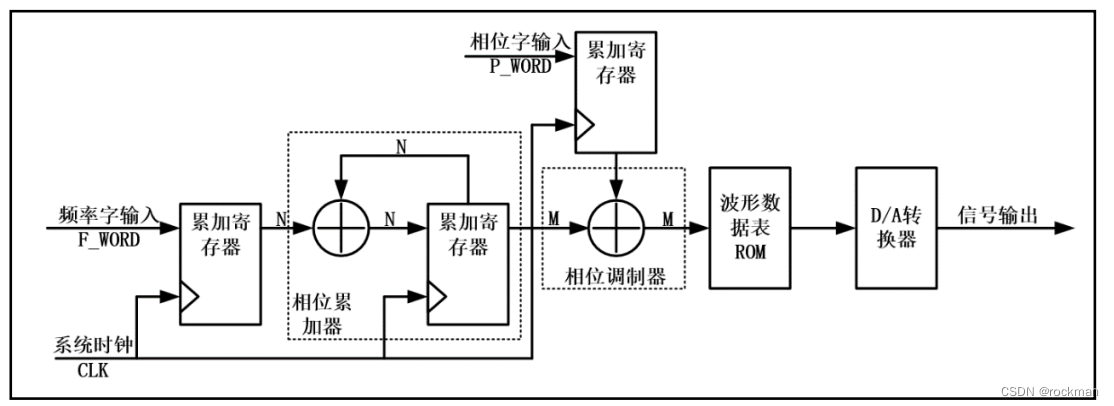
N为累加寄存器的字长，累加器的字长决定分辨率，f_word为频率控制字，决定输出的频率。M为ROM地址线字长，在FPGA实现中，ROM地址直接去累加寄存器的高M位。
DDS工作原理

1、模型分析

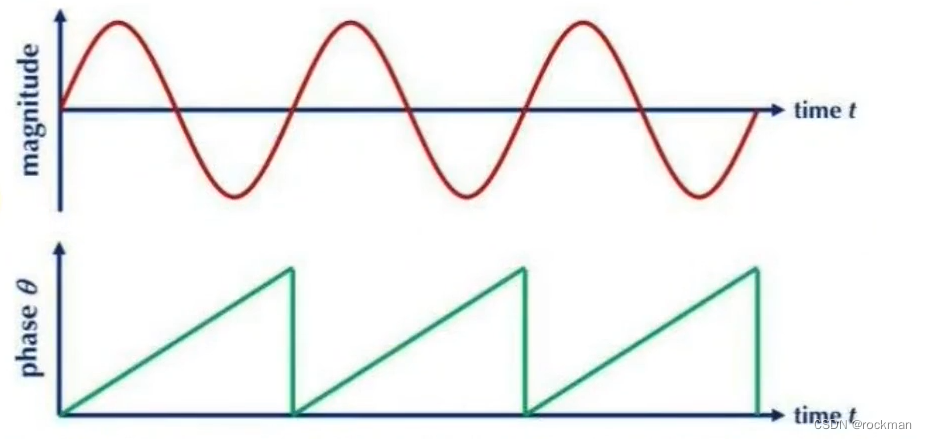
图中分别表示正弦信号和正弦信号的相位。可以看出相位和正弦信号都是周期性波形，且每一相位点对应唯一的正弦信号幅值，它们之间存在一个映射的关系，那么就可以通过相位的值来确定正弦信号的幅度值。

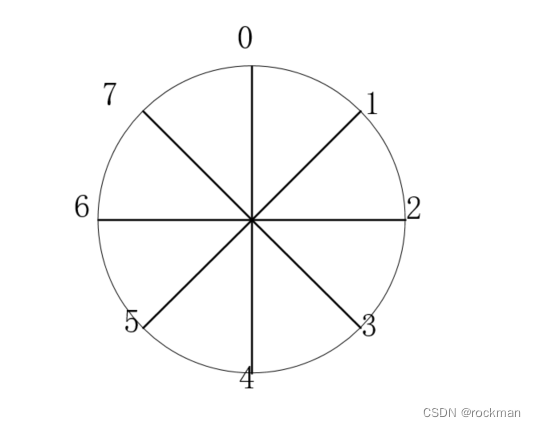
在数字电路中，一个有限位宽的计数器也可以描绘周期性变化。比如一个3bit的计数器，每次加1，当计数到7时会自动归零，变化规律和前面的相位变化规律一样。如果每次加2，计数到7也会归零，速度比加1的快了两倍，相位周期也会缩短一半。若计数器的位宽足够大，表示相位的间隔就越小，能映射的正弦信号波形就越精细。

2、定量分析
假设计数为N位，也就是相位累加器的字长。每次累加的值为k，也即是频率控制字f_word。一次累加时间间隔为Tclk，则累加一周的所需要的时间Tout为

3、映射到数字电路中
在数字电路中，可以通过查表（ROM）的方式来实现这种映射关系。事先把一个周期波形（任意波形）的幅度值存储到ROM当中，使用时根据相位值去查找对应的结果。

Verilog实现DDS
这里使用的DA转换芯片是AD9708，数模转换位数为8位，最大转换速率位125MSPS。内部集成了1.2V的参考电压、运算放大器、电流源和锁存器。AD9708的时序：

因为没有示波器，所以最后没有使用到DA转换。

RTL

module	dds
 (
	
	input	wire			clk		,
	input	wire			rst_n	,
	
	output	wire			da_clk	,
	output	wire	[7:0]	da_data ,
    output  reg     [7:0]   da_datab
 
 );
 
 parameter		F_WORD = 21'd1717987,//频率控制字，输出20Khz
				P_WORD = 1'd0;       //相位控制字
				
reg		[31:0]	fre_add;
reg     [11:0]  addr_reg;
reg     [1:0]   signlist;
reg     [7:0]   q_half;
wire    [7:0]   q_sig;
reg     [9:0]   rd_addr;


always@(posedge clk or negedge rst_n)
	if(rst_n == 1'b0)
		fre_add <= 16'd0;
	else
		fre_add <= fre_add + F_WORD;
		
always@(posedge clk or negedge rst_n)
	if(rst_n == 1'b0)
		addr_reg <= 12'd0;
	else
		addr_reg <= fre_add[31:20] + P_WORD;
	
assign		da_clk = ~clk;



always@(posedge clk or negedge rst_n)
	if(rst_n == 1'b0)
		rd_addr <= 10'd0;
    else    begin
        if(addr_reg[10] == 1'b0)
            rd_addr <= addr_reg[9:0];
        else
            rd_addr <= {10{1'b1}} - addr_reg[9:0];
    end
    



always@(negedge clk)
	q_half <= q_sig;

		  
always@(posedge clk or negedge rst_n)
     if(rst_n == 1'b0)  begin
         da_datab <= 8'd0;
         signlist <= 2'b00;
     end
     else   begin
         signlist <= {signlist[0],addr_reg[11]};
            if(signlist[1] == 1'b0)
                da_datab <= q_half;
            else
                da_datab <= {8{1'b1}} - q_half;
     end   
  //ROM存储波形
rom_f	rom_f_inst (
	.address ( addr_reg ),
	.clock ( clk ),
	.q ( da_data )
	);
 
   //1/4压缩ROM存储波形
rom_wave	rom_wave_inst (
	.address ( rd_addr ),
	.clock ( clk ),
	.q ( q_sig )
	);

 endmodule
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84

testbench

`timescale	1ns/1ns 
module	tb_dds();

reg			clk;
reg			rst_n;

wire		da_clk;
wire	[7:0]	da_data;
wire    [7:0]   da_datab;

initial
	begin
		clk = 1'b0;
		rst_n <= 1'b0;
		#30
		rst_n <= 1'b1;
	end
	
always	#10 clk = ~clk;


dds		dds_inst
(
     . clk         (clk),  //时钟
     . rst_n       (rst_n),  //复位信号，低电平有效


     . da_clk      (da_clk),  //DA(AD9708)驱动时钟,最大支持125Mhz时钟
     . da_data     (da_data),  //读ROM地址
     . da_datab    (da_datab)
  
      );

endmodule
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

可以看到代码使用了两个不同的rom，我在这里对rom进行了压缩了。我们知道，rom内部存储数据越多，占用的资源也就越大。上部分代码中分别实现了rom四分之一压缩和不压缩两种方案。我们往往可以利用信号的周期性和对称性对其进行压缩。例如本文8x4096的rom存储的正弦波数据。

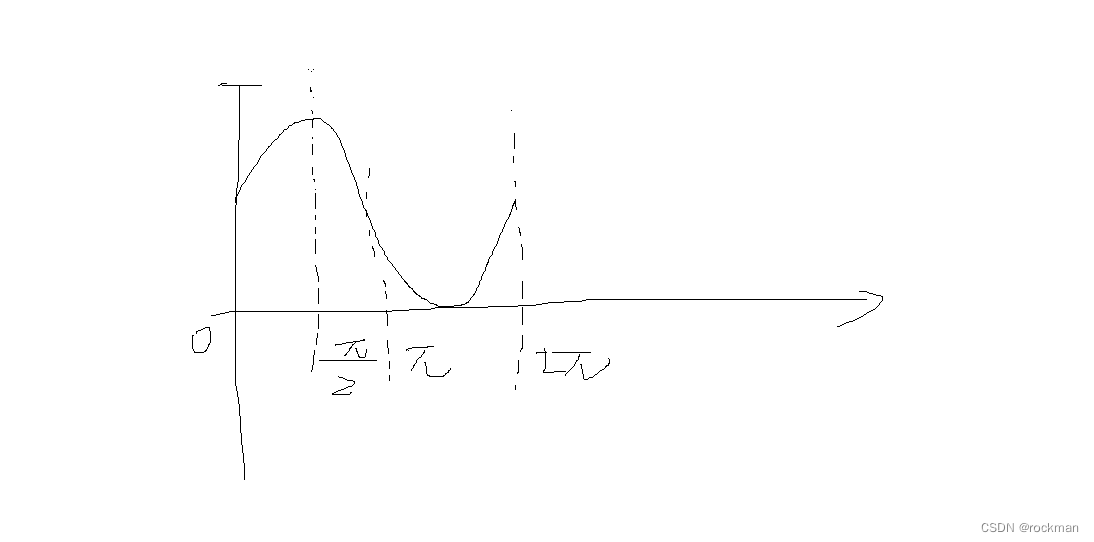
由于正弦波的对称性。我们只用存储0~Π/2的数据，也就是1024数据。当读地址到Π/2时，直接用地址最大值减去读地址，这样就能还原出Π/2到Π直接数据，这是对地址进行了一个小操作。而还原Π到2Π之间的数据，则需要对rom读出的数据进行操作。当寄存地址位addr_reg的第11位为1时，也就是数据输出到达了Π处。这时用数据最大值减去rom读出的数据。这样就能还原出Π到2Π之间的数据。

modelsim仿真结果

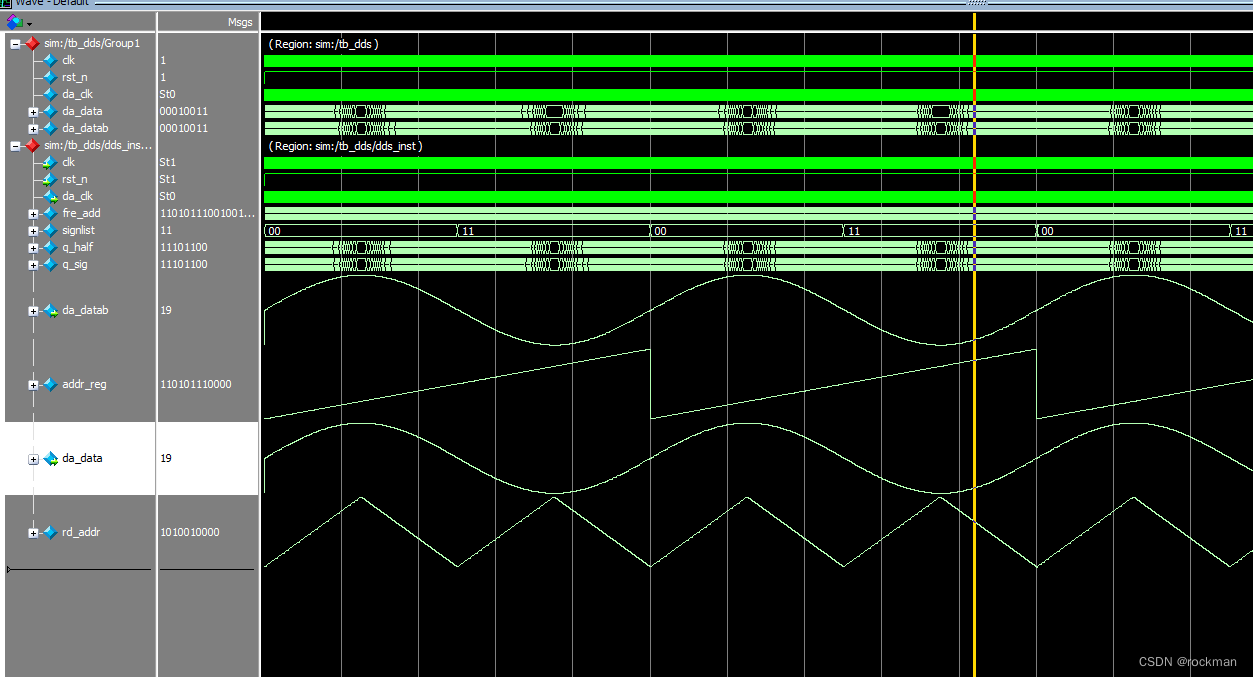
仿真结果位于上方的正弦波是没有经过压缩的，下方的是经过rom压缩的。对比前后，为压缩之前8x4096，压缩了之后8x1024，资源节省了3/4，但是结果相差不大。具体差别多少，可以使用matlab对数据进行fft，再计算两种结果的杂散程度进行对比。其实对rom的压缩的还有其他方法，可以采用桑德兰结构（sunderland）、分层线性插值。